具有标准发生率和Markov切换机制的随机多群组SIR传染病模型*

陈桦剑，韦煜明

（广西师范大学数学与统计学院，广西 桂林 541006）

0 引言

数学模型是描述传染病的重要工具。许多数学模型提供研究传染病传播的根本机制，并提出传染病的控制策略。[1]值得注意的是，Measles、Mumps、Gonorrhea和HIV/AIDS等传染病是在异质人群中传播的。为了描述上述疾病在异质人群中的传播，学者们提出多群组传染病模型。[2]一个异质人群可以通过传播方式、接触模式、地理分布划分为几个同质群组，使得群组内部和群组之间的相互作用可以分别建立模型。最早的多群组传染病模型之一是由Lajmanovich和Yorke根据Gonorrhea的传播提出的。[3]从那时起多群组传染病模型的成果逐渐呈现在世人面前。[4–8]

实际上，自然界中存在多种噪声，如白噪声和电报噪声。确定性传染病模型无法准确描述这些噪声对传染病传播的影响。因此，传染病模型中的参数并不是确定的常数，而是随着环境中的连续扰动而围绕着某些均值扰动。为了更好地揭示环境白噪声的影响，学者们将参数扰动引入传染病模型中，[9–12]例如Cao等人对两群组的SIRS传染病模型中的疾病传播率βkk进行扰动，[13]得到了模型（1）:

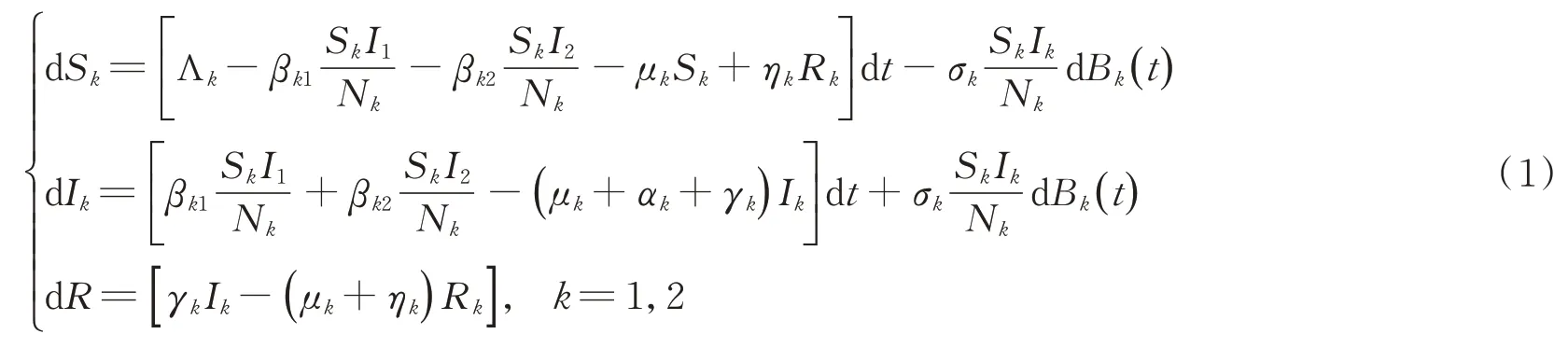
模型（1）各参数含义如下：Λk是表示在第k(k=1,2)个群组的人口输入常率，βkj表示Sk和Ij(j=1,2)间的有效接触率，μk表示在第k个群组中S、I、R各仓室中的自然死亡率，γk为第k个群组中染病个体的恢复率，ηk为第k个群组中免疫者失去免疫后重新变为易感者的比率，αk则表示第k个群组中染病个体的因病死亡率。假设参数γk、ηk和αk是非负的,而Λk、μk和βkj是正的，特别地,Bk表示相互独立的标准布朗运动,σk是白噪声强度，k,j=1,2。

除了白噪声之外，电报噪声对传染病模型也有影响。例如，传染病模型中的有效接触率βkj在不同的季节影响下有很大的不同。学者们通常使用有限状态空间中连续时间的Markov链模拟环境状态的随机切换。[14–17]连续时间Markov链通过Markov状态切换得到传染病模型中主要参数的变化。对于人类而言，研究疾病的有效传播率βkj受到环境波动影响比研究其他参数更有意义。因此，Liu和Jiang提出了一个带标准发生率和Markov切换的多群组随机SIS传染病模型，只对仓室Sk和Ij间的疾病有效传播率βkj进行扰动：[18]

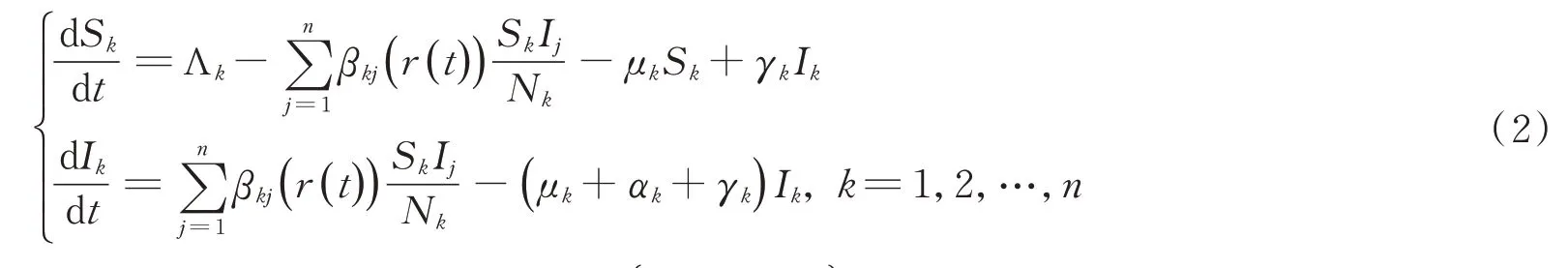
其中，有效传播率βkj是一个同质连续时间Markov链{r(t),t≥0}在一个代表不同环境的有限状态空间S={1,2,…,N}中取得的，Markov链{r(t),t≥0}是由转移速率矩阵Γ=(δij)N×N产生的。

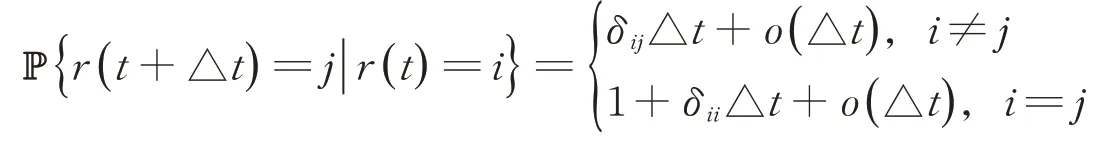
其中，△t>0表示一个小的时间间隔，δij表示从状态i切换到状态j的转移速率，δij≥0，当i≠j时，有成立。对∀l∈S，βkj(l)均为正常数。

受到模型（1）和模型（2）的启发，笔者提出一项具有标准发生率和Markov切换机制的随机多群组SIR传染病模型：

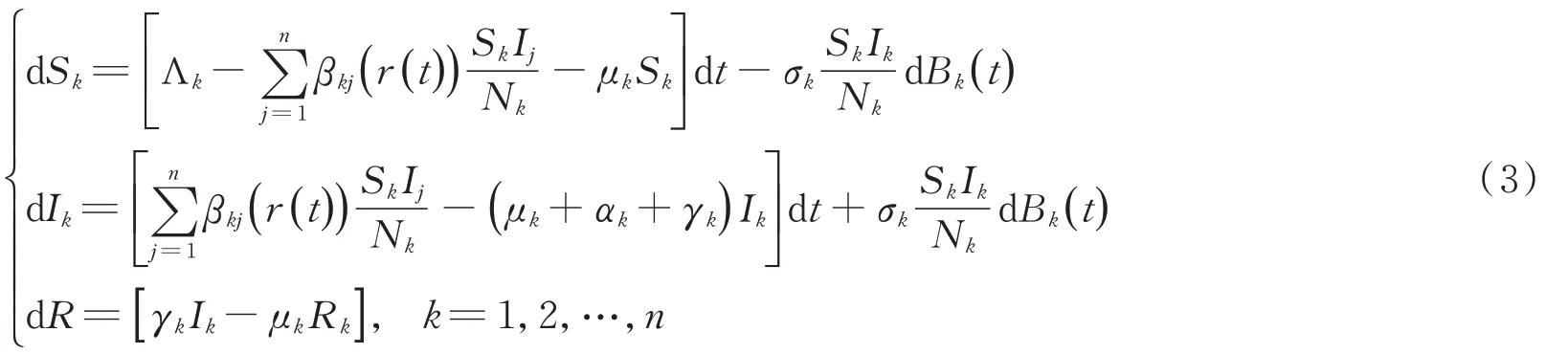
模型（3）中各参数的意义与模型（1）和模型（2）保持一致。沿用Liu和Jiang的设定，本文假设Markov链是不可约的，也就意味着系统可以从一个机制切换到另一个机制。[18]对于∀i,j∈S，存在有限数i1,i2,…,il∈S使得δi,i1,δi1,i2,…,δil,j>0，根据有限状态的马尔科夫理论，可以推断其拥有遍历性质。注意到Γ总是拥有一个平凡特征值，由于Markov链是不可约的，因此rank(Γ)=N-1。在上述条件下，Markov链拥有唯一一个平稳概率分布π=(π1,π2,…,πN)∈R1×N。此外，这个平稳分布可通过求πΓ=0确定，服从于且πi>0,∀i∈S。

定义Rd+={x=(x1,x2,…,xd)∈Rd:xi>0,1≤i≤d}。令表示一个带参考族{Ft}t≥0的完备概率空间，并且满足一般条件：{Ft}t≥0单调递增右连续，且F0包含所有零测集。对任意的常数列{g(i):i∈S}，定义。系统（3）前两个方程均与R无关，为了方便，下文仅对模型（4）进行讨论。

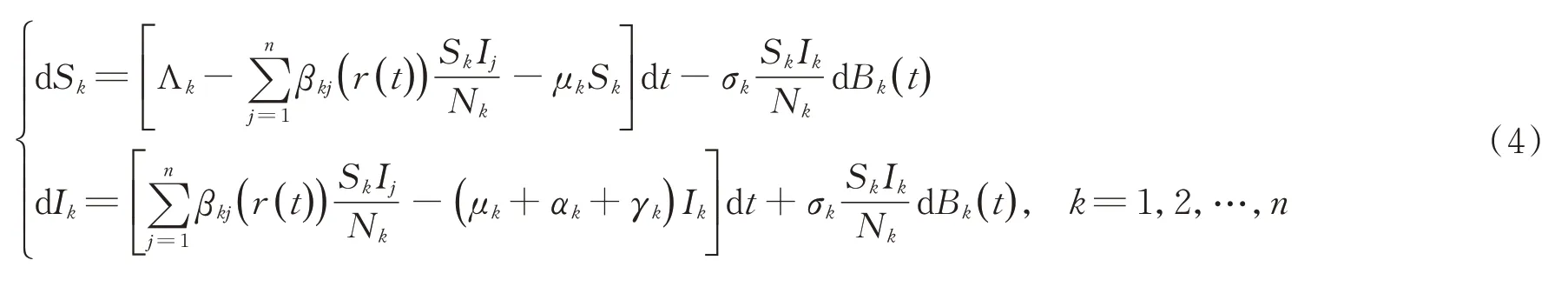
1 全局正解的存在唯一性

本节证明模型（4）全局正解的存在性。

定理1对于任意初始值(S1(0),I1(0),…,Sn(0),In(0),r(0))∈×S，系统（4）存在一个唯一正解(S1(t),I1(t),…,Sn(t),In(t),r(t))，此正解以概率1保持在×S中，换言之，即

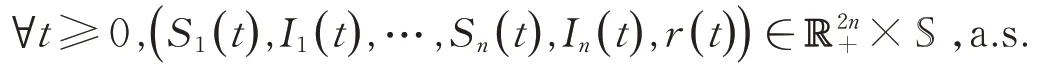
证明：由系统（4）可知，系统（4）中的系数满足局部的Lipschitz条件，对于给定的初始值(S1(0),I1(0),…,Sn(0),In(0),r(0))∈×S，系统（4）存在一个局部解(S1(t),I1(t),…,Sn(t),In(t),r(t))，∀t∈[-τ,τe]，其中τe是爆破时间。

只有证τe=+∞，a.s.，才能说明解(S1(t),I1(t),…,Sn(t),In(t),r(t))是全局的。

令m0≥0充分大，使得Sk(0)，Ik(0)(k=1,2,…,n)均在区间中。对任意整数m≥m0，定义一个停时：

τm=inf{t∈[0，τe)：min{Sk(t)，Ik(t)，k=1，2，…，n}≤或max{Sk(t)，Ik(t)，k=1，2，…，n}≥m}

本文定义inf∅=∞（∅表示空集）。根据停时的定义可知，当m→∞，τm是单调递增的，记，因此τ∞≤τe，a.s.若τ∞=+∞，a.s.，则τe=+∞，a.s.，说明解(S1(t),I1(t),…,Sn(t),In(t),r(t))是全局的。

下面利用反证法证明。假设τ∞<+∞，则存在两个正常数T和ε∈(0,1)，使得P{τ∞≤T}>ε。因此，存在m1≤m0，使得P{τm≤T}>ε，∀m≤m1。

一方面，∀t≤tm，对于任意k(k=1,2,…,n)均有

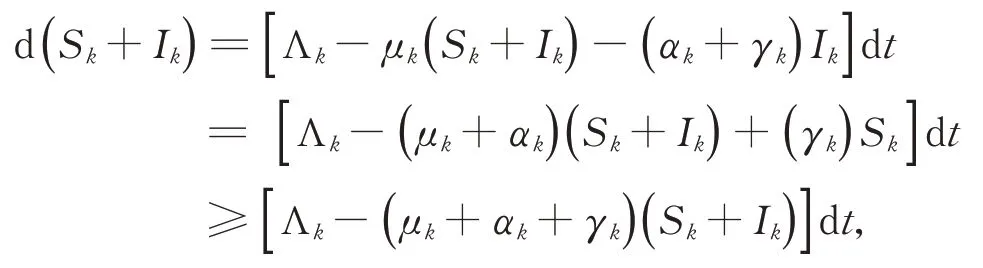
可得

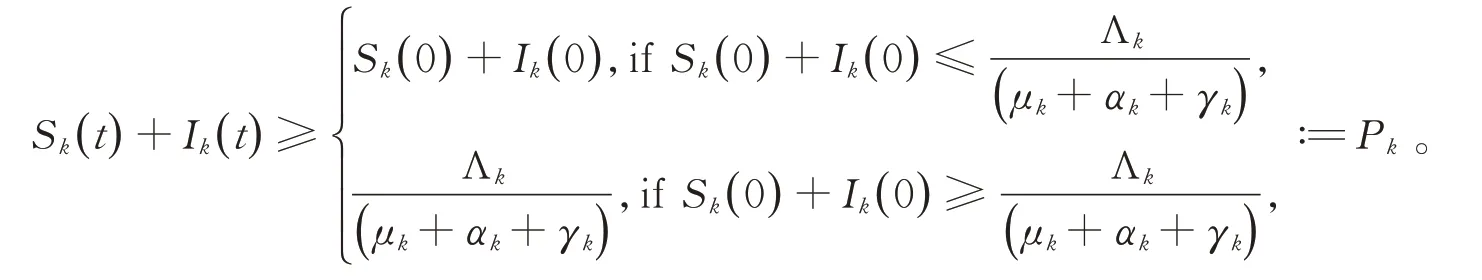
另一方面，∀t≤tm，对于任意k(k=1,2,…,n)均有

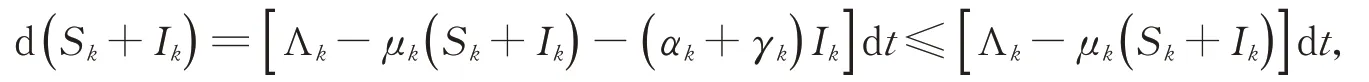
可得

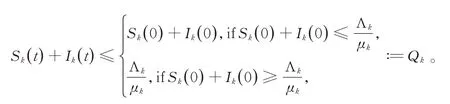
定义一个C2函数，

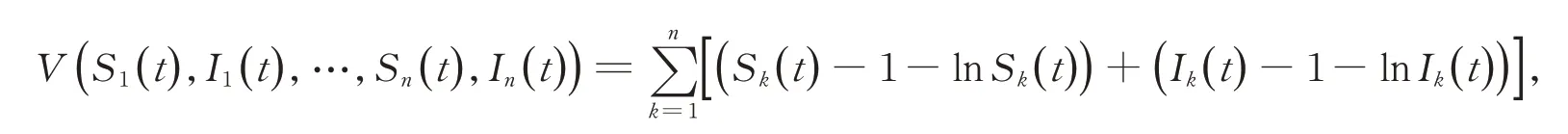
显然，函数u-1-lnu≥0,∀u>0是非负的，对C2函数V应用Itô公式，可获得

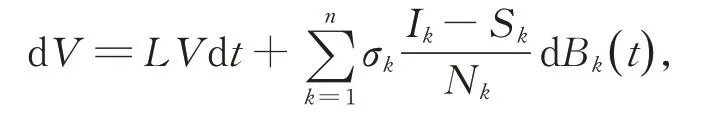
其中，

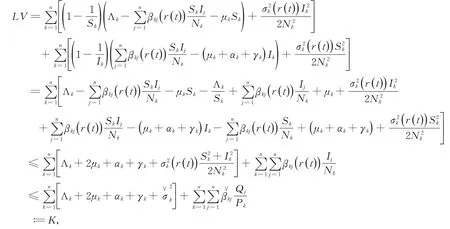
K是一个正常数。余下的证明与Dalal等证明类似，[19]故在此忽略。

由此可以证得：系统（4）存在一个唯一正解(S1(t),I1(t),…,Sn(t),In(t),r(t))，此正解以概率1保持在×S中。

注意1:对任意初始值(S1(0),I1(0),…,Sn(0),In(0),r(0))∈×S，模型（4）存在一个唯一正解(S1(t),I1(t),…,Sn(t),In(t),r(t))∈×S，因此

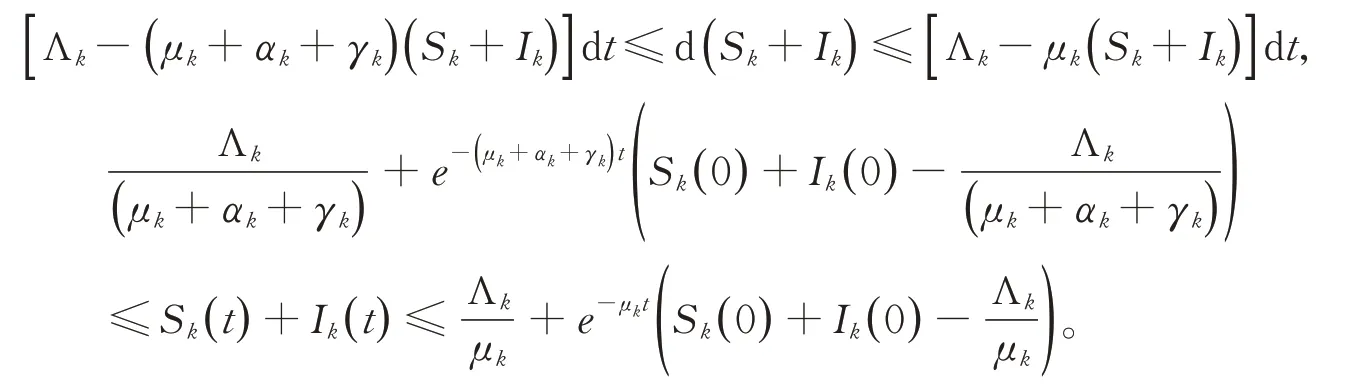
是系统（4）的一个正不变集。

2 传染病的灭绝与持久

本节讨论具有标准发生率和Markov切换机制的随机多群组SIR传染病模型（4）灭绝与持久的充分条件。

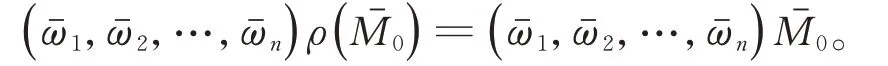
2.1 传染病的灭绝

定理2假设是不可约的，令(S1(t),I1(t),…,Sn(t),In(t),r(t))∈×S是传染病模型（4）带初始值(S1(0),I1(0),…,Sn(0),In(0),r(0))∈Γ′×S的一个解。如果下列任意一个条件成立：

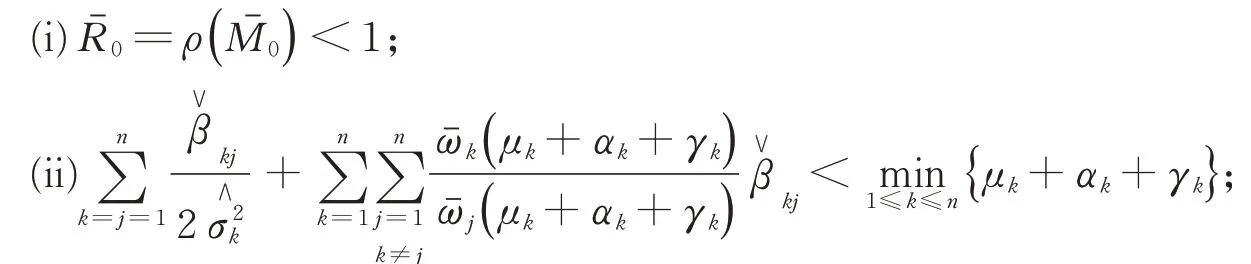
则传染病Ik(k=1,2,…,n)依概率以1灭绝，即=0,a.s.,k=1,2,…,n。

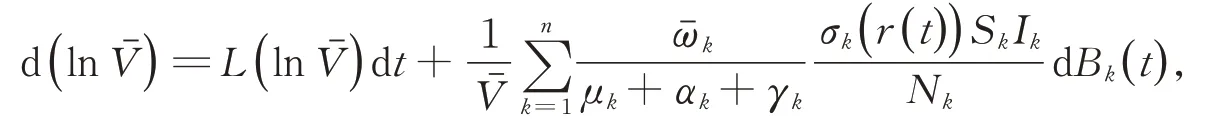
其中，

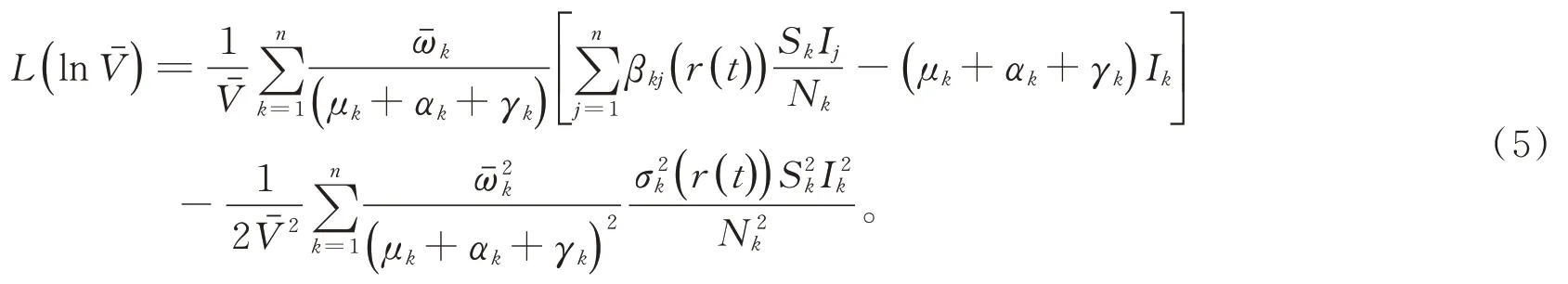
情况1：当条件（i）成立,有

因而,

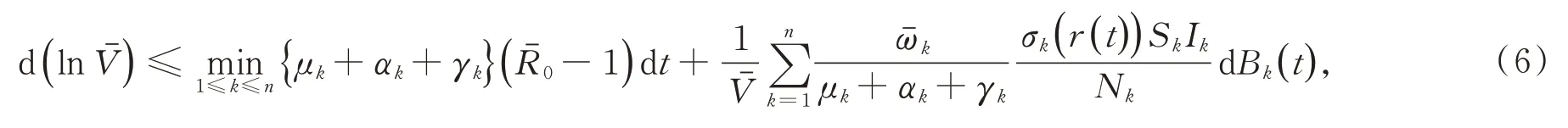
对（6）两边从0到t积分，并除以t

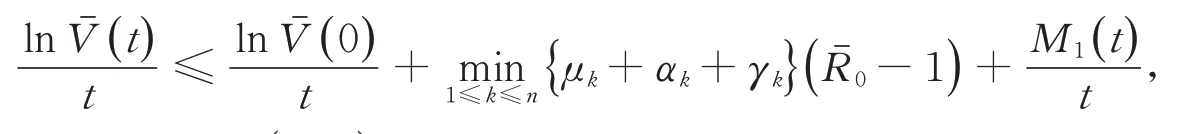
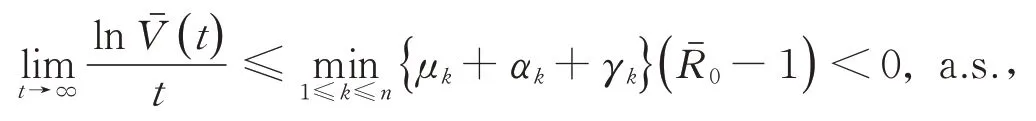
因此,

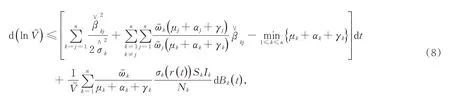
对（8）两边从0到t积分，并除以t，得到

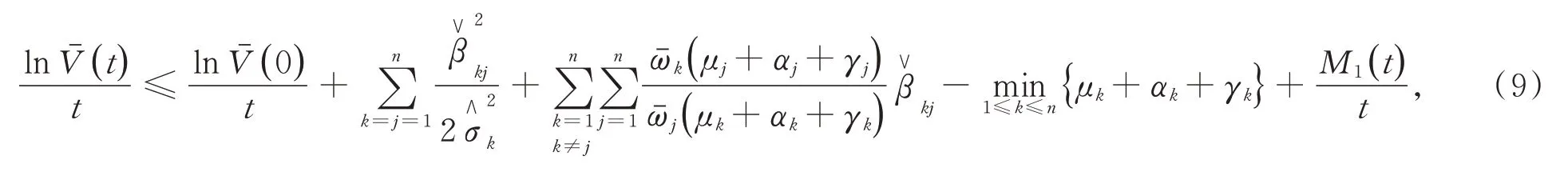
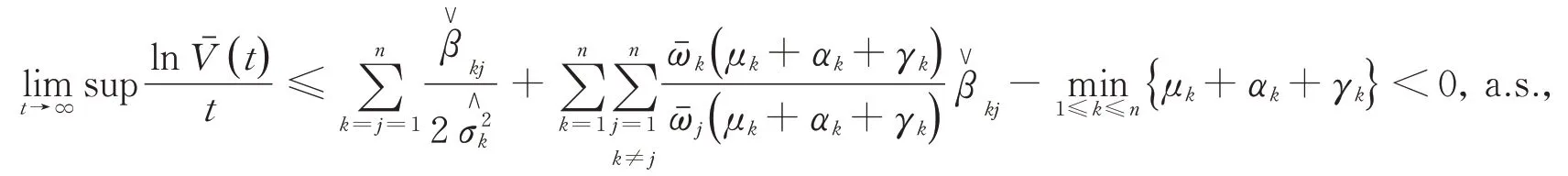
2.2 传染病的持久

本小节给出传染病持久的充分条件。

定义假设存在一个正常数c，如果>c>0,a.s.,(k=1,2,…,n)，则称x(t)持久。

定理3假设是不可约的,(S1(t),I1(t),…,Sn(t),In(t),r(t))∈×S是传染病模型（4）带初始值(S1(0),I1(0),…,Sn(0),In(0),r(0))∈Γ′×S的 一 个解。当，且时，传染病Ik(k=1,2,…,n)将持久存在。

证明：定义一个函数V1(I1,I2,…,In)=，运用Itô公式，得到

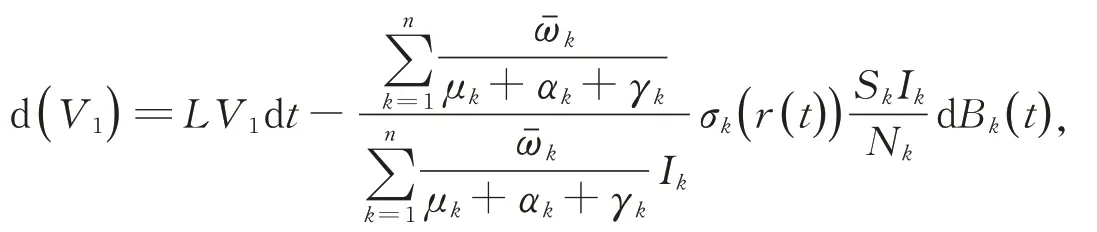
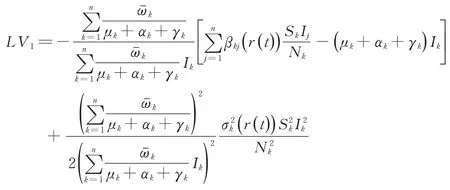
其中，

另一方面，定义V2(I1)=-I1，得到

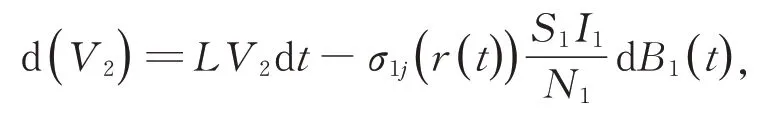
其中

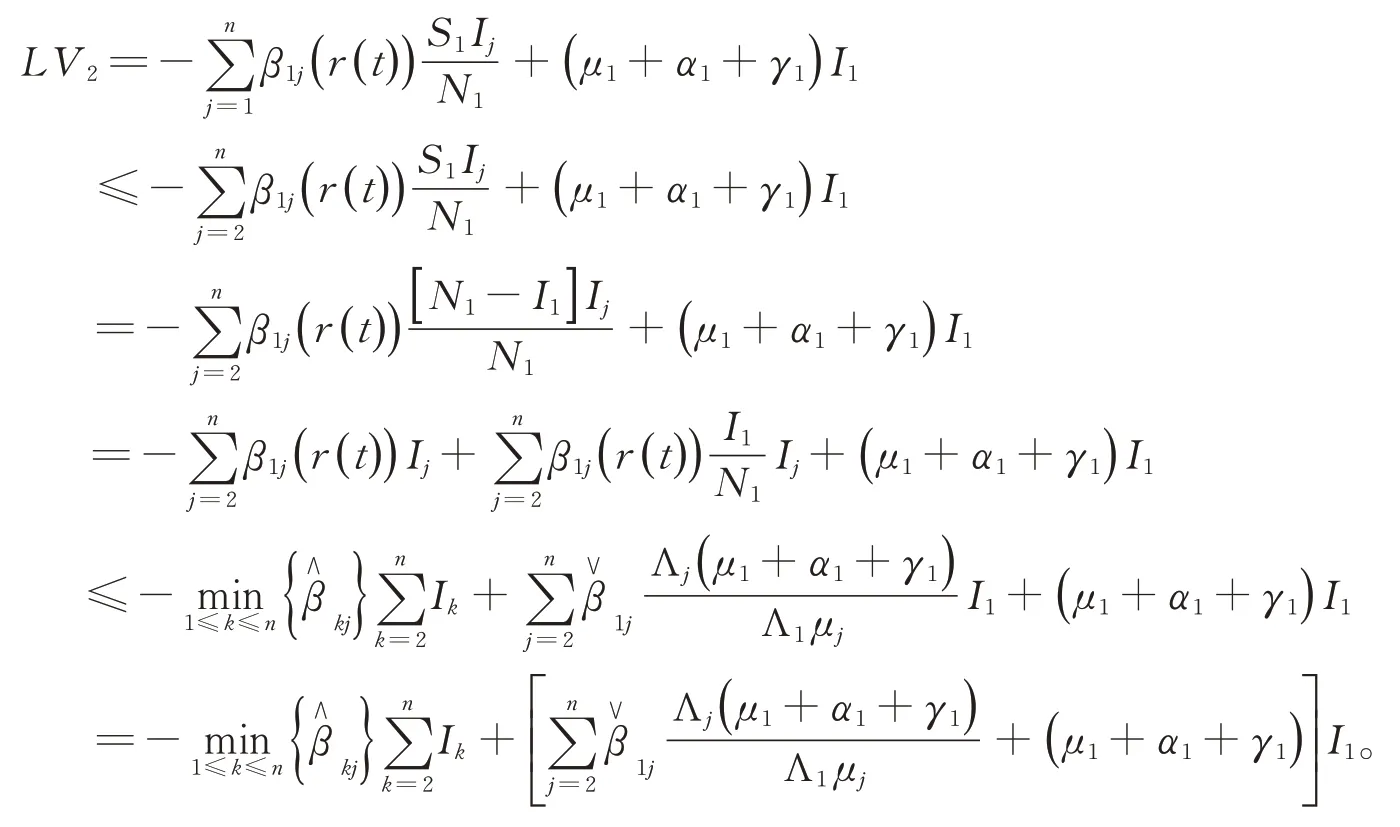
综合考虑，定义

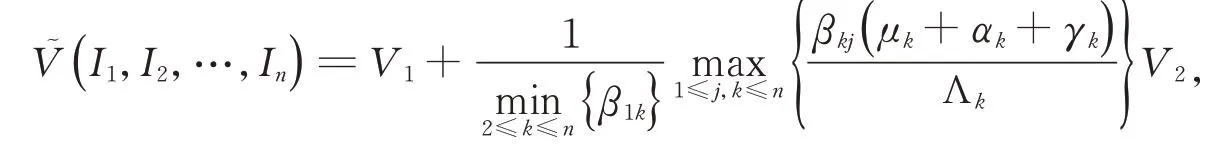
从而

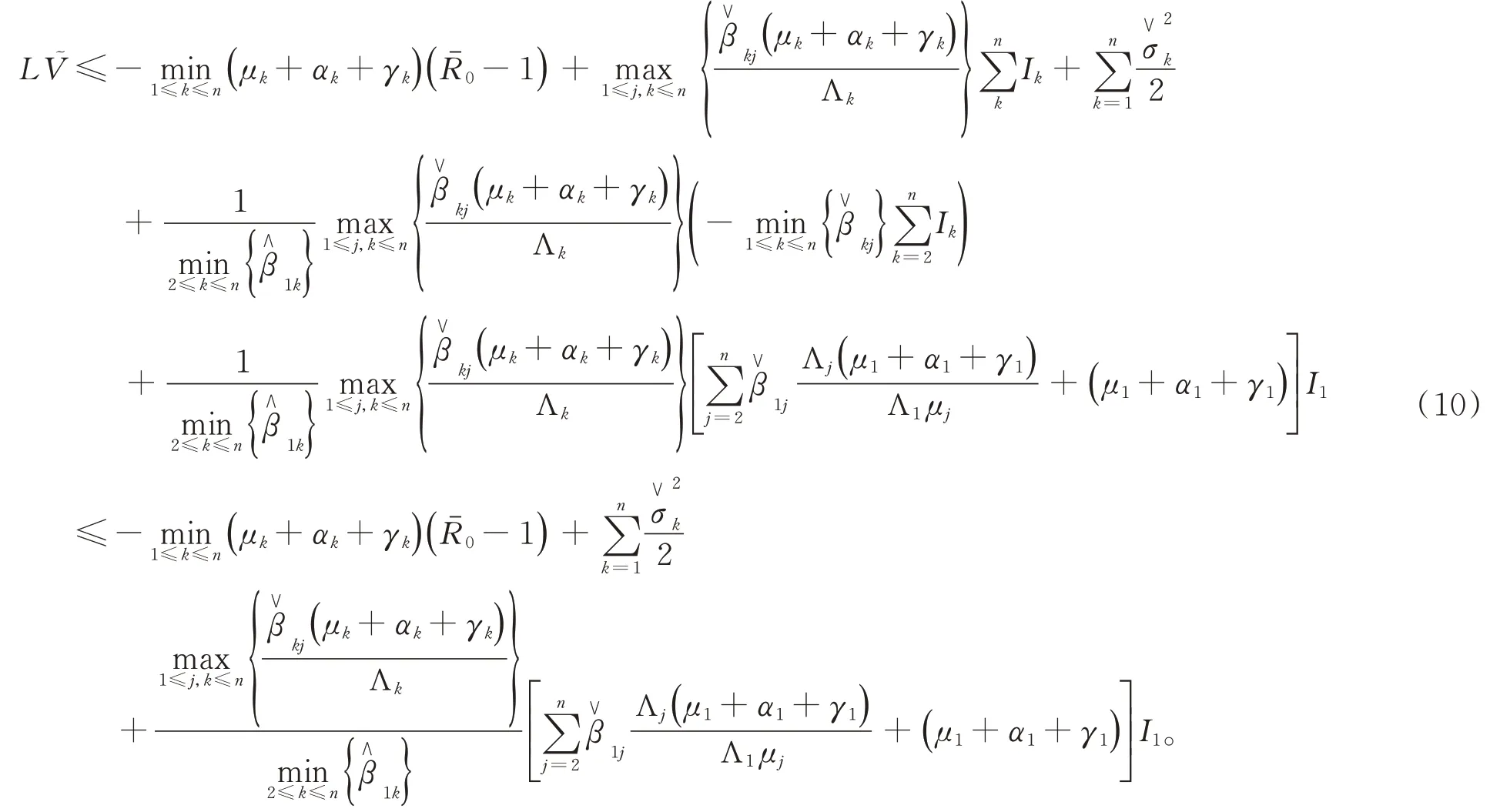
结合强大数定律，将（10）式从0到t积分，并除以t，得到

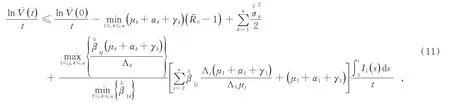
对（11）式进行变换，有

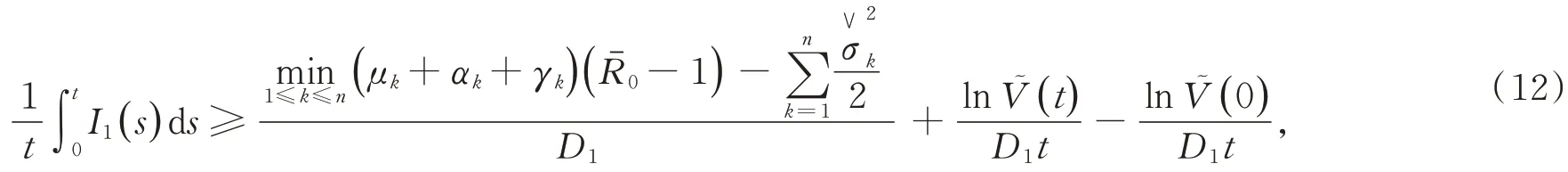
其中

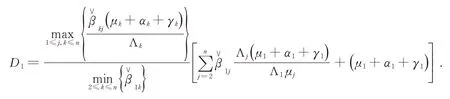
取（12）式下极限,可以得到

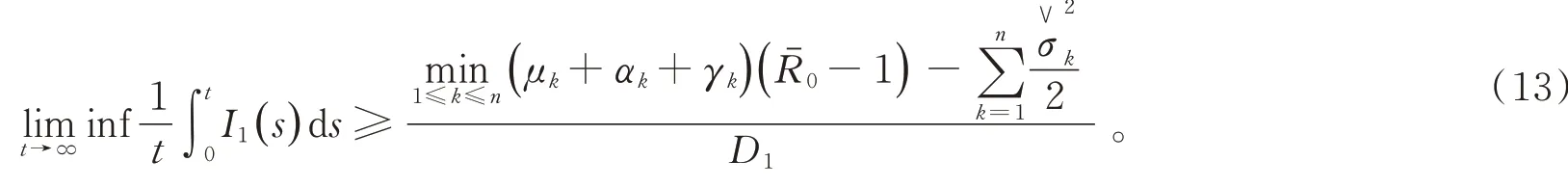
当定理3中的条件成立时，有

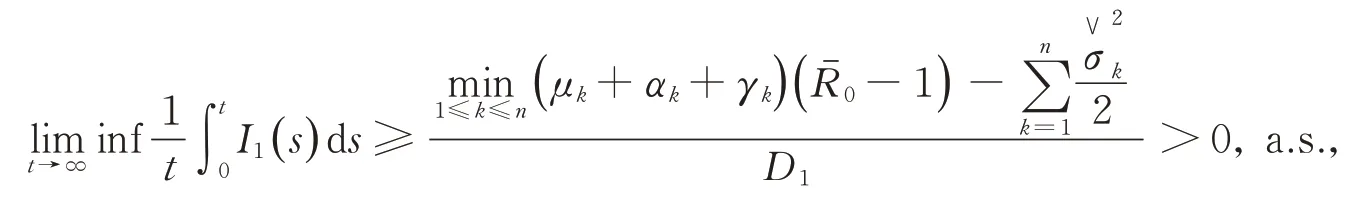
由此，我们可以推断疾病I1将灭绝。

类似地，我们也可以得到

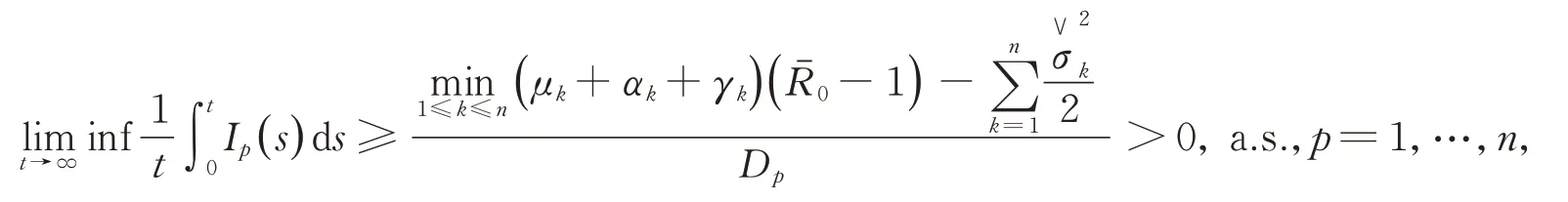
其中

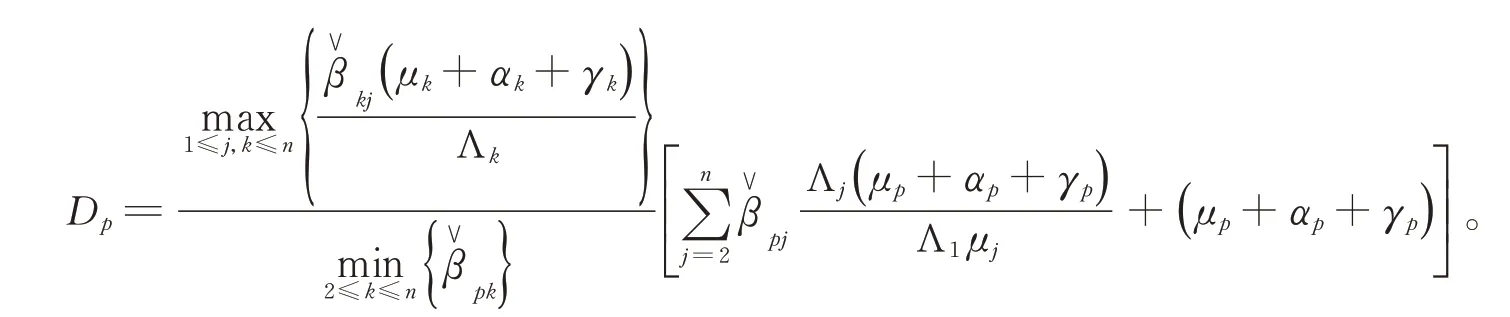
因此，传染病Ik(k=1,2,…,n)将持久存在，定理3得证。

3 模型实例

在本节中提供两个例子证实上述证明结果。为了简便，此时取S={1,2}，k,j=1,2，讨论两个群组之间的传染病传播情况。

例1参考文献[21]有如下取值:

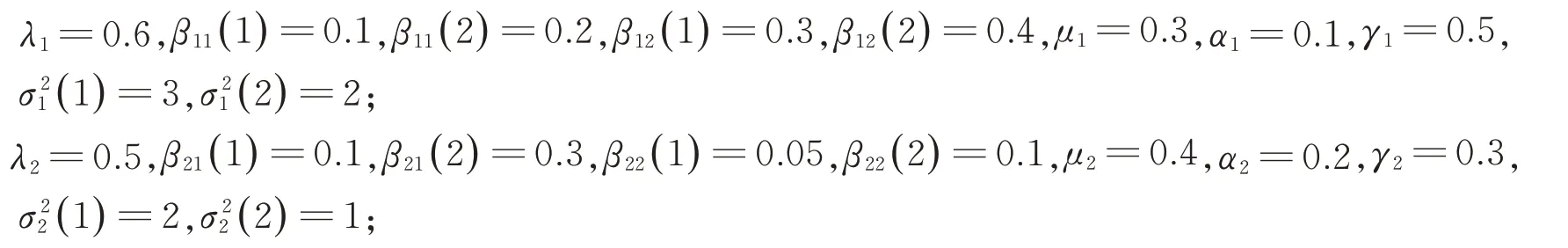
Case 1.

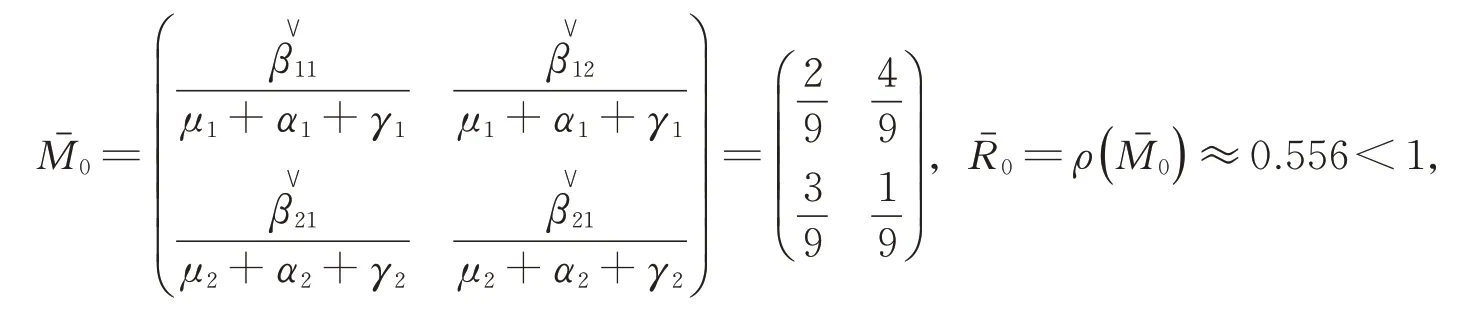
满足定理2中的条件（i）,此时传染病依概率以1灭绝。

Case 2.

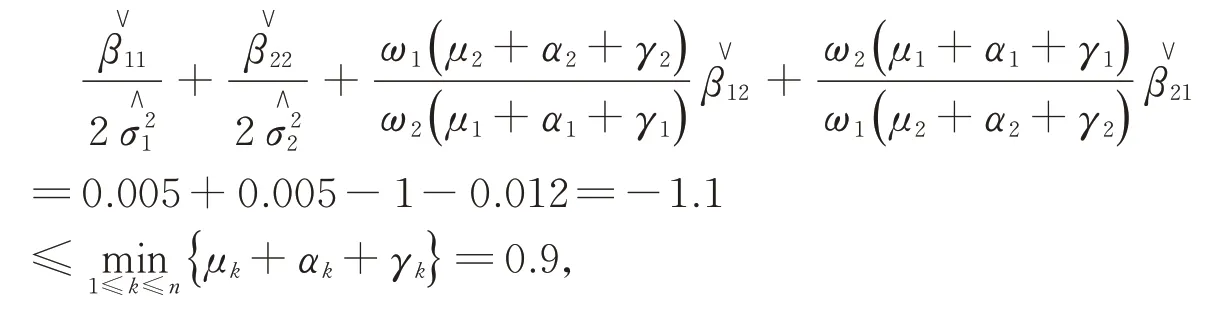
满足定理2中的条件（ii），此时传染病依概率以1灭绝。

例2取值如下:

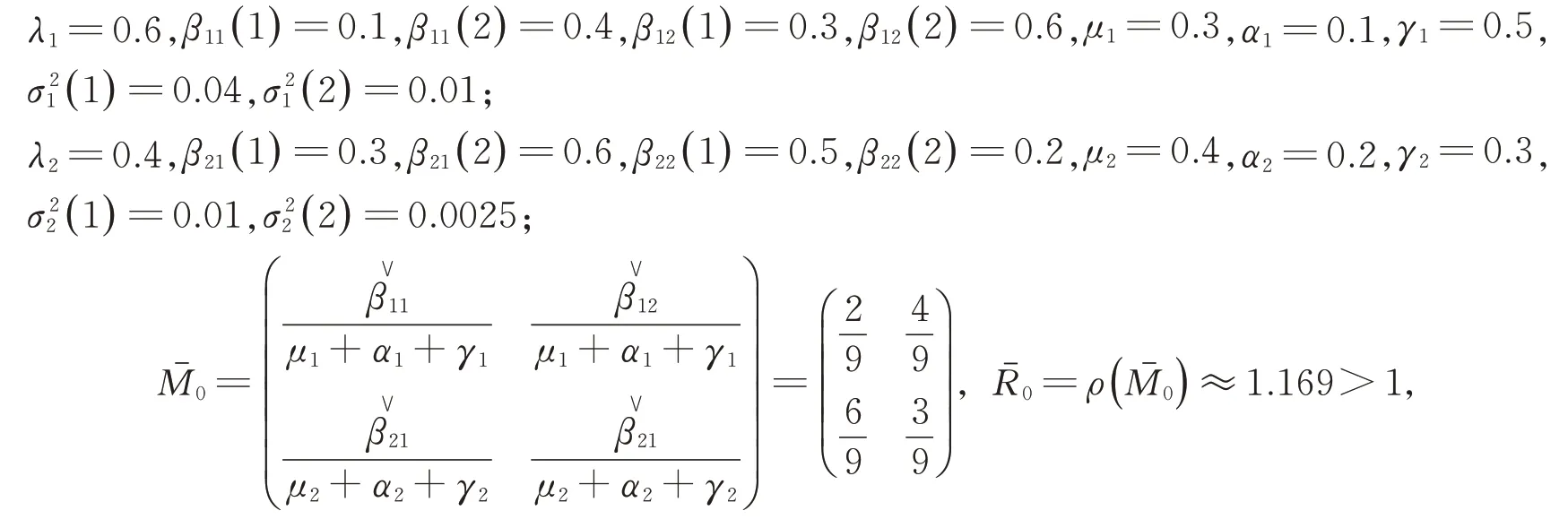
且

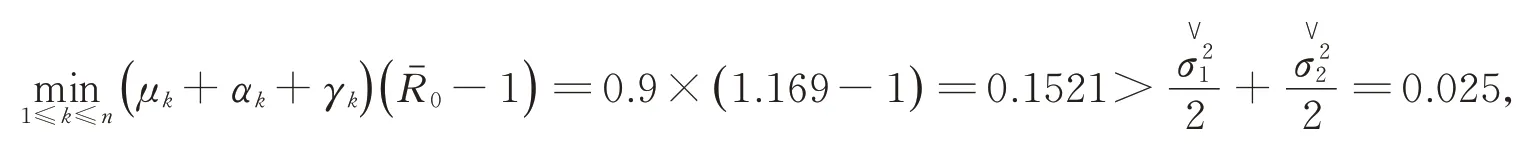
满足定理3中的条件，此时传染病持久存在。

4 结论

本文研究一项具有标准发生率和Markov切换机制的随机多群组SIR传染病模型。通过构建Lyapunov函数和运用随机分析学理论，讨论了模型的全局正解的存在唯一性。其次，文中建立了传染病灭绝和持久的充分条件：

如果下列任意一个条件成立，

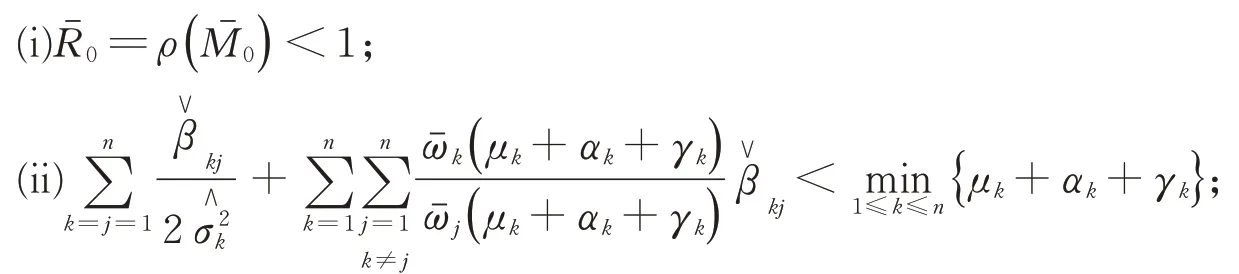
则传染病Ik(k=1,2,…,n)依概率以1灭绝。

最后，文章用例子验证理论研究的合理性。