“益积”和“翻法”研究*

周畅，段耀勇

（1.西安邮电大学 理学院，陕西 西安 710121；2.中国人民警察大学 智慧警务学院，河北 廊坊 065000）

开方术的产生起源于一元高次方程的求解问题。《九章算术》中已有相对完整的开方术程序，开平方和开立方都有一个带从开方的例子。之后经刘徽等人改进的开方术一直沿用到唐朝。宋元时期，先后出现了贾宪立成释锁开方和贾宪増乘开方，然后经历了立成释锁和增乘开方短暂并存的时期，后发展为秦九韶的正负开方术,而又趋于完善为朱世杰的正负开方。到明朝和清朝初期，中算家的开方是现在算盘上使用立成释锁方法完成的，正负开方术已无人会用。直到汪莱、李锐时代，中算家才重拾宋元的正负开方术着手研究了高次方程的求解问题，并得到了一些诸如笛卡儿符号法则、韦达定理等方程论方面的结论。[1]

1 中国开方术的发展阶段

为了更清楚地描述“益积”和“翻法”的身世，我们按历史时间顺序以开方算法自身的特点将中国的开方术分为五个阶段，即前刘益“九章”开方、刘益开方、秦九韶-朱世杰开方、明朝珠算立成释锁开方以及焦循-李锐开方。

1.1 前刘益“九章”开方

前刘益“九章”开方具有四个特点：一是沿袭九章的开方法可以称为前立成释锁开方法，开方所用如“1-2-1”和“1-3-3-1”的二项式定理的系数还是规定的；二是首项系数为“1”；三是开方中“实”为正，即方程的常数项写在方程右边，这具有强烈的现实和几何意义，因为“实”可能为面积或者体积；四是减根的最后一步经刘徽改进为“减实”。对应的方程为x2=N(N>0)，x3=N(N>0)和x2+Bx=A(A>0,B>0)，时称开带从方。后来，祖冲之提出了“开差幂”和“开差立”属于“开带从平方”和“开带从立方”的内容，可惜没有文献传世。唐朝的王孝通在《缉古算经》中记载了许多如x3+Bx2+Cx=A(A>0，B>0,C>0)用开带从立方求得一个正根的题目，书中还有一个x4+px2=N的方程是用两次开平方得到结果的。

1.2 刘益开方

在宋朝已出现“立成释锁”和“增乘开方”两种开任意高次方的方法。刘益开方稍后于贾宪，他的“减从术”和“翻积术”开方运算说明他熟悉增乘开方，其开方对应的方程为xn+a1xn-1+a2xn-2+…+an-1x=an，ai>0,i=1,2,3,…,n，即方程的首项系数为“1”且所有系数均为正数，无论是立成释锁还是增乘开方，减根的最后一步都是“减实”。当然，刘益在中国古代数学史上最先引入系数可为负数的方程,并突破了方程首项系数必须为1的限制，这种根本性的改变对原来的算法会带来灾难和冲击。[2]刘益开方方程的改变会对原来的开方框架产生冲击，或者说原来的开方结构已无法解释新情况，因无法被接纳所以需要新的解释正名。

1.3 秦九韶-朱世杰开方

“增乘开方”由贾宪所创，经杨辉等人的推广和传播，到13世纪已成系统，即以“增乘开方法”为主导的求高次方程正根的方法已经发展得十分完备。秦九韶的“正负开方术”在中国数学史上首次提出“以方约实”的估根方法。秦九韶、李冶、朱世杰等在开方过程中遇“换骨”“投胎”则继续开方，遇到系数是无理数的情况，则进行了有理化处理。对方程的最高次项系数出现不为“1”的情况，李冶、朱世杰等便创造了通过变量代换化最高次项系数为“1”的方法来处理得“之分术”，又称为“连枝同体术”。

此时方程的各个系数基本上已无限制，只是秦九韶的増乘开方要求“实常为负”，如果实为正，则方程各项都乘以-1，同解化为“实常为负”。他这样做，一是可以将开方减根最后一步“减实”变为加法，使开方程序高度统一起来；二是可以保证开方的实与九章开方相同，原来的正统一变成了负。这是秦九韶继续解释刘益的“益积”和“翻法”的原因，他只是把开方的“实”移到了方程的左边，减根的最后一步已从“减实”变成“加实”。

李冶和朱世杰的开方已无“实常为负”的限制，至此，増乘开方法中各系数（包括常数）全程都带符号参与严格的、彻底的“边乘边加”运算。

1.4 明朝珠算立成释锁开方

元朝仍然以筹算为主，明初开始逐渐以珠算为主，最迟在明正德嘉靖年间珠算完全取代了筹算，清初数学家已经完全不懂筹算了。由于开方术比较复杂，在珠算用于加减乘除法之后，才用于开方。由于明朝时期“增乘开方法”失传，珠算开方在中国算学史乃至世界数学史上也是很有特色的。此时在算盘上利用立成释锁方法开方，这种方法较增乘开方复杂，但是方程的系数（包括常数）已经没有任何限制，所以“益积”和“翻法”问题会变得更加复杂。关于2次、3次 和4次方程，则需要提到吴敬、顾应祥、周述学和孔广森四位数学家。[3]顾应祥对各种开带从方的论述最为全面，在《测圆海镜分类释术》中有六十多个开带从方的程序说明，包括2次、3次和4次方程，涉及“益积”“减从”和“翻积”等各种不同的题型类别。

此时的开方特点，系数不带符号参与运算，减根最后一步“减实”。

1.5 焦循-李锐开方

清中叶之后，人们重新发现“增乘开方法”，几乎所有著名的数学家都投入到对秦九韶等开方术的研究。“谈天三友”汪莱、李锐、焦循互相切磋辩诘，讨论了方程的分类及根与系数的关系。这里，焦循使用的是秦九韶的开方法，而李锐用的则是朱世杰的方法，所以焦循会继续深化、完备刘益和秦九韶的“益积”和“翻法”问题。李锐和朱世杰一样认为开方只是一个单纯的计算程序，无需讨论计算细节中的问题。而且李锐的开方较朱世杰更进一步，开方可以开得负商，所以商也带符号参与开方运算。

2 “翻法”和“益积术”的产生

刘益前的开方因为所有系数都是正数，“实”也是正数，所以开方过程就是通过不断“减实”使其变为0，此时开尽；或者逐渐变小，此时开方不尽，带奇零。而刘益的“益积术”“减从”“翻积”“益隅”，都是因为开方中系数出现了负数，所以开方过程中“减实”与以往的经验相比会发生异变，可能出现“实”越来越大或者干脆变号的情况。如此情况下，“益积”和“翻积”出现了。下面以两个例题说明这两种方法，为了叙述方便将筹码改为阿拉伯数字。

与之前的方程不同，x2-12x=864出现了“负从”（-12），为此刘益提出“益积术”与“减从术”解决这个问题。图1为“益积术”，使用的是九章开方法。[4]

按照《九章算术》的开方程序，首次估根为30，那么应该用30×(30-12)减根，但是因为这有悖既有的开方程序的语法，所以对于30×(30-12)=900-360，先 将-360益 积为864+360=1224，然后再归结为合乎《九章算术》开方语法的程序进行减实。同理，倍根为60，用他估得方程的第二位根是6，按照《九章算术》的减根应为((60+6)+(-12))×6=324，这同样也不符合既有的语法，所以对于((60+6)+(-12))×6=324，将72益积为72+324=396，然后减实，尽。

刘益的“翻法”，其中负隅的符号不是单独考虑的，与九章算术开方不同，864-900出现了负数，这与原来开方中“实”会减至0，或越来越小不同，因此，此处称之为“翻积”，“实”发生了质的改变。可以说脱胎换骨了，如钱宝琮在《增乘开方法的历史发展》中指出的“投胎”“换骨”本来是神仙家的术语……在某些条件下减根后的方程必须“投胎”“换骨”……目的是在指导开方的人放心地开下去，不要因为“实”数有不寻常的转变而缩手缩脚，不敢继续开方。后来秦九韶称“翻积”（翻法）为“换骨”，这里的开方算法是増乘开方。

-x2+60x=864出现了“益隅”（-1），为此刘益提出“翻积术”解决这个问题。图2为“翻积术”，使用的是增乘方法。[4]64

图2 翻积术

在中算家那里,解方程与开方是同义语,其方法有着鲜明的几何背景。由于负系数的引入,使得释锁开方的几何意义在某些情形下掩而不显。刘益关于翻法的讨论亦为秦九韶等继承并发扬光大。引入负系数之后,方程根的个数、议商的方法问题等都较以前复杂得多,刘益讨论了“翻积”“翻从”等,同时也留下了许多问题未及讨论。

综上，无论是“益积”“减从”还是“益隅”，都不过是因为开方时系数出现了负数，也就是说方程中有的负系数，这是不符合《九章算术》开方的语法的，所以刘益通过将负数部分产生“减实”的数值，事先加到“实”（被开方数）上的方式来处理。此时，开方式已合乎系数都为正的情况，然后再按《九章算术》开方程序处理即可。这里如果古人不拘于《九章算术》系数为正的开方术的限制，直接负数带着符号进行原有的程序计算的话，一种先进的开方法“增乘开方”便呼之欲出。如果考虑符号开方，无论是“益积”“益隅”还是“减纵”，开方的操作程序将会大大简化，这正是“增乘开方”的优越性所在。

3 易名“换骨”“投胎”及其完备与消亡

关于易名“换骨”和“投胎”，清阮元《畴人传》（卷二二·宋四·秦九韶）：“……其遥度圆城术，以开九乘方得数，运算尤为繁赜。略诸术所载开方图，正负、加减、益积、翻法、说之尤详。凡开平、开立及开三乘以上方，通一为道，有投胎、换骨、玲珑、连枝诸目。”从前面的论述来看，刘益的“益积”和“翻积”都是由开方过程中系数出现了负号所致。秦九韶等继承并发扬光大了刘益的“益积”和“翻积”方法。秦九韶的増乘开方要求“实常为负”，开方减根最后一步变为“加实”。秦九韶的正负开方运算中符号没有“直接”参与运算程序，而是采用了标注的方式完成，清朝的焦循采用了秦九韶的开方法继续研究了“益积”和“翻法”，并完备了这个问题。

关于“益积”和“翻法”的完备，清朝数学家焦循在《开方通释》中总结了“投胎”和“换骨”的方法，并给出了“益积”和“翻法”条件：“秦氏于商两次者，有投胎、换骨二法。投胎即益积，方与实同名相加也。换骨即翻积，方与实异名相消也。大约和在隅，乃有益积，和在方乃有翻积。和在隅，益方大于初商，则益积。初商大于益方，则不益积。和在方，较数小于初商，则翻积。初商小于较数，则不翻积。皆随数目之多寡，而自然得之，非有成法也。”也就是说开方时，根据具体情况来定是“投胎”（益积）还是“换骨”（翻积），没有事先给定判断方法。

这两个例题分别是解方程-x2+27x-72=0（图3）和-x2+54x-720=0（图4），都开得24的例子，从结果上来看,这两个题目似乎也是焦循构造出来的。[5]第一个方程开方翻积，第二个不翻积。这里需要指出，焦循与秦九韶相同正负开方正负号标注，带符号的加法只需“同加异减”即可，使用的是刘徽正负数的运算法则：“同名相除，异名相益，正无入负之，负无入正之。异名相除，同名相益，正无入正之，负无入负之。”

图3 例题-x2+27x-72=0

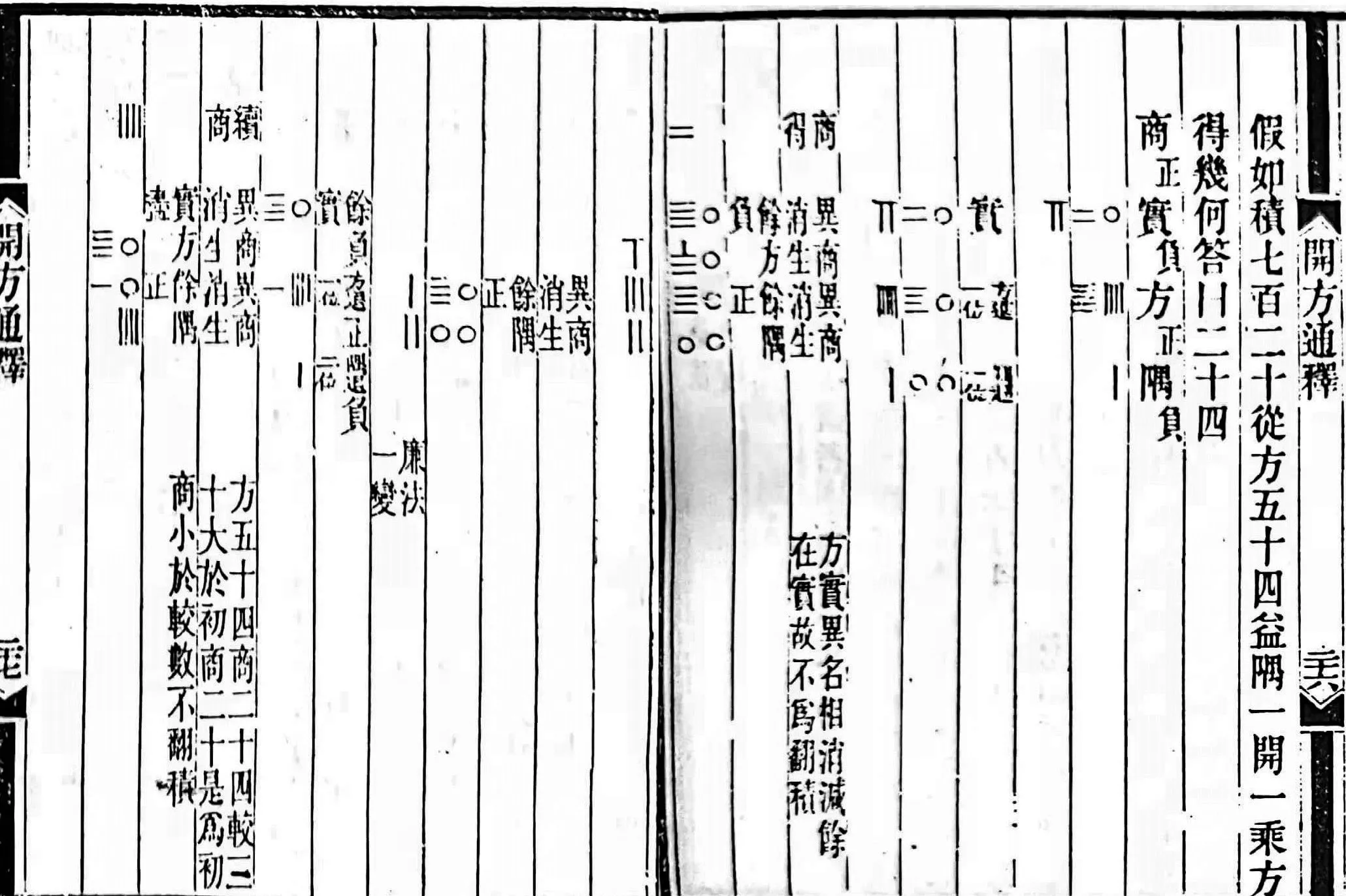
图4 例题-x2+54x-720=0

这里焦循构造x2-21x-72=0（图5）和x2-19x-120=0（图6），都是开得24的例子。[5]1463-14644第一个开方因为“方实同名”而“益积”，第二个因为“方实异名”而“不益积”。

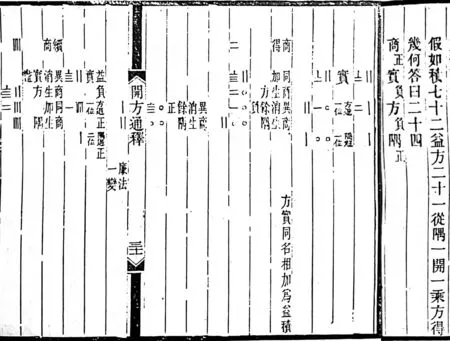
图5 例题x2-21x-72=0

图6 例题x2-19x-120=0

从刘益和秦九韶处理的一种情况的两种变体来看，“实”无论是正还是负都可能存在“益积”（投胎）和“翻积”（换骨）的问题，只是李冶称秦九韶的“换骨”为“翻法”或者“倒积”，不限于此，如果开方导致一次项符号改变也称“翻法”，比如-1.75x2+108x-1449=0，开方中常数项和一次项系数都变号了，李冶称之为“倒积倒从开平方”，实际上推广了“翻法”，此题即翻积又翻从。其益积开方与秦九韶相同，朱世杰对此就更不太关注了，比如他在《算学启蒙》“开方释锁”有7个题目说是用“翻法”，但是实际情况是其中一个题目符号都没改变，其余6题只是一次项或二次项符号改变，常数项未变号。另外《四元玉鉴》“端匹互隐”门第一问和“两仪合辙”门第11问开方都需要“倒积”（翻法/换骨），但是朱世杰没提此事，此时开方已是计算程序，无需再讨论开方中“实”或“系数符号”的变号问题。[6]

而李锐和朱世杰所采用的增乘开方，方程的系数带着符号进行“边乘边加”运算，亦无“实常为负”的要求（这个要求和九章开方运算一致，只是从秦九韶开始把九章的“正实”写成了他在方程中为负的形式）。刘益时，“实”写作“正”，当“隅”或“从”出现负号时，“减实”为0或者越来越小的惯例可能会被打破，如前所述，当“正实”变大或者变号时就是所谓的“益积”和“翻积”。秦九韶则将“实”按照方程的常数项系数写出来，增乘开方时减根最后一步由“减实”变成“加实”，完备统一了开方程序。同样，当这个“负实”在开方运算中绝对值变大即为“投胎”，称谓也容易理解；当他由负变正时就是“换骨”。朱世杰和李锐（商可以为负）的增乘开方，其方程的系数、常数项和商都带符号参与开方运算，算式中系数带符号。对于可能会出现的“益积”或“翻积”的情况，也变得无需讨论了，此时已没有必要关注开方中的常数项是否变号或者绝对值变大，或者方程的其他系数符号发生改变的情况，正负开方只是单纯求得一元高次方程的一个根的程序。

图7是一个李锐求得方程负根的例子。[9]其中，在标注方程各系数（包括常数项）的符号外，其符号也在系数中标注出来，这一点与李冶和朱世杰相同。这里的正负开方只需要按程序计算就行，系数带符号，常数项带符号，商也可以带符号。之前的开方中，商是不带位值参与计算，乘后数值大小由开方各系数的位置决定。[7]所以朱世杰只是有了舍弃“益积”和“翻法”的倾向，李锐才是彻底放弃这些说法的践行者。对李锐的开方来说，“常数项的变号”（系数的变号）或者实绝对值变大都没有意义，随后的相关讨论也是无源之水了。

图7 李锐求得负根的例子

尽管李锐之后无需讨论“益积”和“翻法”，但是这些问题在明朝的珠算开方中却异常丰富，这与珠算开方的过程密切相关。

4 在珠算开方中的繁荣发展

如蒙语中马身体的各部位都有特定名称和因纽特语中有诸多关于白色的词汇一样，在开方算法中也有与计算细节相关的各种称谓。“翻法”和“益积”就是这样的例子。从刘益的“益积术”和道古“正负开方”中“脱胎”“换骨”“玲珑”法开始，经吴敬、顾应祥和周述学分别对二次方程归为13、15和18类；再到孔广森对3次方程和4次方程的归纳分类；最后到汪莱基于方程“可知”的概念对高次方程重新分类而完备。明朝珠算开方方程仍然“实常为负”，自然存在“翻法”和“益积”的问题，所以，在明朝的开方运算过程中出现了以“益积”和“翻法”为核心词汇的开方算法的分类，实际上这是根据其开方过程某一步骤的特点而取的名称。

4.1 顾应祥对方程的分类

顾应祥所著的《测圆海镜分类释术》研究并且注释了《测圆海镜》，于1550年成书。他将《测圆海镜》的全部问题重新加以分类，厘为十卷，仍得170问，每问之后有释，释后有术，对问题解答的演算过程详加推导，并对其中的开方、开带从方过程一一写明（表1,表2）。

表1 吴敬分类

表2 顾应祥分类

顾应祥在吴敬二次方程分类的基础上，使得这部分内容更加丰富和全面,[3]118-123顾应祥算书中载有不同系数符号的一元二次方程的解法，如对一元二次方程Ax2+Bx=C(A≠0)来说，顾应祥一般称二次项系数A为隅，一次项系数B为从，C一般被称为实数且为正。当A=1,B>0,C>0时，他称用带从开平方法求解，这和吴敬《九章比类》相同，而杨辉、王文素、程大位等称之为“益从开平方”；当A>1,B=0,C>0时，用负隅开平方法求解，等等。相较于顾应祥的其他算书，其《测圆海镜分类释术》中介绍的带从开方法最为全面。另外，顾应祥还对3次方程和4次方程[3]118-141进行了分类，分别对应着17种和7种形式。

4.2 周述学对方程的分类

周述学是明代后期（约16世纪）著名的科学家。他所著的数学著作《神道大编历宗算会》简称《历宗算会》，全书十五卷。他在《历宗算会》中继续研究二次方程的分类问题，分为18类情况。[3]118-127表3是周述学《历宗算会》开带从平方法分类。

表3 周述学《历宗算会》开带从平方法分类

这里，不难发现以开方算法中的特点对方程的归类已成传统，其中出现的所有的名称都与“带从”“益积”（倒积）、“翻法”“益隅”“减实”“减从”等进行组合得到，原因很简单，珠算开方用“立成释锁”逐渐发展为“珠算开方”，这里运算各系数都不带符号运算，需要对方程的各系数（包括常数）“是否变号”和“实”的绝对值是否会出现增大的情况、开方的各系数是否为负都需要作为开方过程中的异变标注出来，也就出现上述丰富的开方分类内容，但是实际上更多的开方运算细节的标准，并非严格意义上的方程分类。