插装阀阀芯优化与仿真分析*

王欲进，潘思意

(1.太原学院，太原市，030032；2.太原科技大学机械工程学院，太原市，030024)

0 引言

液压技术在拖拉机、播种施肥机、收获机械、植保机械等机具上都有广泛地应用。插装阀作为液压系统重要的组成部分，其性能决定了液压系统的响应速度。同时，插装阀阀芯与阀套间的摩擦力、卡紧力严重影响插装阀的响应速度，更严重的会导致阀芯卡死而出现安全事故。

目前对于阀芯结构以及阀芯阀套间隙研究的专家学者数不胜数，陈佳等[1]通过对矩形槽滑阀卡紧力的研究，建立了带有矩形槽的阀芯、阀套间隙侧压力分布的数学模型，经过修正后的数学模型可较好地模拟滑阀间隙的无因次侧压力分布，其可为均压槽的优化设计提供理论依据。陆亮等[2]通过对伺服阀静态卡滞问题研究，得到增大阀芯与阀套初始半径间隙或减小小球偏离阀芯轴线的初始偏心量,均可以提高阀芯不卡滞的输出压力阈值。张俊俊等[3]通过研究均压槽的位置和结构尺寸对卡紧力的影响关系，得到了均压槽的最优位置及合理的结构尺寸。Hong等[4]设计一种新型的带有螺旋槽的液压滑阀，其研究表明带有螺旋槽的滑阀能完全释放线轴周围不对称的压力分布。刘李平[5]对滑阀阀芯、阀套间隙的流动状态进行仿真分析。研究了阀芯运动和阀芯不动时，阀芯与阀套之间间隙的大小、两端压差大小，以及阀芯与阀套间的泄漏量、径向力、卡紧力的大小，该研究为液压阀的设计和性能优化提供依据。Rajda等[6]提出了通过修改滑阀阀芯的几何形状进而减小压力值，研究表明对称底切的使用减少了径向力的不均匀性。Tan等[7]通过CFD仿真描述了阻尼法兰及其参数对补偿效果的影响，得到了最优参数，获得了最优的阻尼结构。Pan等[8]通过分析伺服阀滑阀在层流和湍流条件下的流量特性，并提出了一种适用于层流和湍流的通用孔板流量数学模型，然后根据仿真和试验验证了该模型的重要性。Filo等[9]通过构建差动开关阀阀芯几何形状，并进行CFD仿真，得到了新形状的阀芯对其工作范围具有显著作用。Agh等[10]设计了一种新型凹轮喷嘴结构的旋转比例流量控制阀，并进行了CFD仿真分析，最后得到新提出的阀门在理论计算与仿真分析条件下，在稳态和瞬态下都有很好的一致性。Xie等[11]提出了在锥形阀芯尾部引入阻尼尾的结构，该优化结构能补偿作用在插装阀阀芯上的稳态液动力。

针对插装阀长时间工作导致的阀芯与阀套结合面产生的磨损问题，本文提出一种新型的插装阀阀芯结构。结合缝隙流动和液压卡紧理论，求解出基于N-S方程、伯努利方程和卡紧力方程的阀芯与阀套间卡紧力与压差的关系方程。建立流体动力学仿真模型，研究新型阀芯和原阀芯在相同入口压力条件下，阀芯与阀套间隙的压力、切线应力的分布规律。

1 插装阀间隙卡紧力数学分析

插装阀是由插入元件、控制盖板、通道块三大部分组成。插入元件由阀芯、阀套、弹簧和密封件组成[12-16]。图1为插装阀的剖视图。图2为插装阀阀芯、阀套结构示意图。

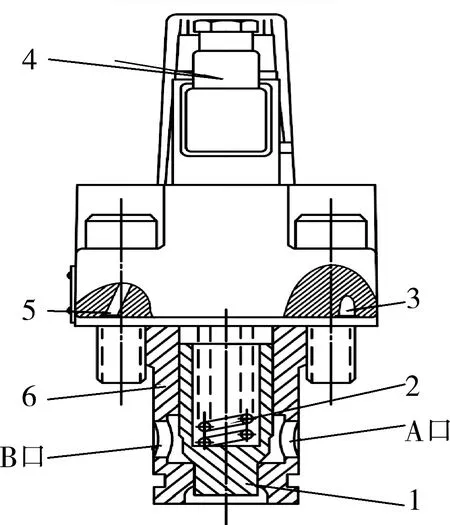
图1 插装阀剖视图Fig.1 Sectional view of cartridge valve1.阀芯 2.弹簧 3.外泄油口Y 4.先导控制器 5.外泄油口X 6.阀套

图2 插装阀阀芯、阀套结构示意图Fig.2 Cartridge valve spool,valve sleeve structure diagram

直径为D2的阀芯放在直径为D1的阀套中，并且阀套静止，阀芯以速度U在阀套间运动，根据相对运动，在此假设阀芯保持静止，阀套以速度U反向运动，进口和出口的压力分别为P1和P2。具体工作参数如表1所示。

表1 插装阀理论分析参数名称及释义Tab.1 Cartridge valve theoretical analysis parameters and interpretation of the name

根据插装阀间隙示意图，将阀芯与阀套间的受力分析分为三步进行求解，然后再整合受力分析。这样可以更好地分析新型阀芯与原阀芯模型的优点。

根据纳维斯托克斯方程、动量方程、伯努利方程、流量连续性方程对新型阀芯开有导流槽的部分进行受力分析。

1)纳维斯托克斯方程。假设间隙内的流体为理想流体，忽略动力粘度系数所带来的影响，列出了阀芯与阀套间隙的N-S方程。

(1)

式中：X——x方向质量力；

Y——y方向质量力；

Z——z方向质量力。

在重力场中单位质量力为X=Y=0，Z=-g,在缝隙中建立平面坐标系，液压油沿x轴方向流动速度为u，沿y轴和z轴方向的速度都为0，通过已知条件对N-S方程进行简化，得

(2)

式中：-g——z方向的重力加速度。

由简化后的方程可得，沿x轴方向压力梯度变化近似为0，对式(2)中的第3个方程进行积分得

P=-ρgz+f(x)

(3)

(4)

(5)

对z积分两次，可得到

(6)

式中：l——间隙的长度。

根据边界条件，当z=0，u=0，可得沿x轴方向的速度表达式

(7)

当z=h,u=U可得沿x轴方向的速度表达式

(8)

式中：U——阀套的运动速度。

对式(8)进行简化，去除无关小量，最后得到速度

(9)

2)伯努利方程。对于均压槽间的导流槽，由于导流槽的长度近似为其水力半径的2～4倍，所以导流槽可近似看作为阻尼孔来进行受力分析。由于导流槽环绕了阀芯整个圆周，具有对称性，在这里只对1/12导流槽进行分析。列出s-s截面和r-r截面的伯努利方程

(10)

式中：vr——r-r间隙油液的速度；

vs——s-s间隙油液的速度。

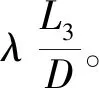
从均压槽到导流槽再到均压槽，根据流量连续性方程得

vsAs=vdAd=vrAr

(11)

式中：vd——d-d间隙油液的速度；

As——s-s间隙的面积；

Ad——d-d间隙的面积；

Ar——r-r间隙的面积。

油液从r-r截面到d-d截面为一扩散过程，由动量定理

ρAvd(β2v-βdvd)=(Pd-P2)A

(12)

将式(10)～式(12)进行联立整合

(13)

再将式(13)与式(9)进行联立可得到相邻均压槽间的压差

(14)

通过式(14)可以得到开有导流槽的部分压差值，大小为3ΔP。

3)卡紧力。在缝隙流动中，因为压差会引起阀芯在阀套内发生倾斜，进而导致阀芯与阀套接触挤压，由此引发卡紧现象。当产生卡紧现象时，卡紧力的大小可根据式(15)计算得到。

(15)

Fk=KlD2(P1-P2)

(16)

式中：K——卡紧力系数；

Δδ——平均间隙差；

δm——平均间隙。

阀芯与阀套间的卡紧力系数K与t=Δδ/δm的关系如图3所示。未加工导流槽和均压槽部分阀芯与阀套间的卡紧力

图3 阀芯卡紧力系数K与t的关系图Fig.3 Diagram of spool clamping force coefficient K versus t

(17)

带有导流槽和均压槽部分阀芯受到的卡紧力：

(18)

式中：lx——为带有导流槽和均压槽部分间隙的长度。

2 模型建立与仿真设置

2.1 三维建模

为了验证所提出的新型阀芯的性能，利用SolidWorks软件对阀芯与阀套的间隙进行建模得到如图4所示的三维模型，图4(a)为原阀芯间隙的全剖视图；图4(b)为新型阀芯间隙的全剖视图，这里选取阀芯与阀套的间隙为0.04 mm。

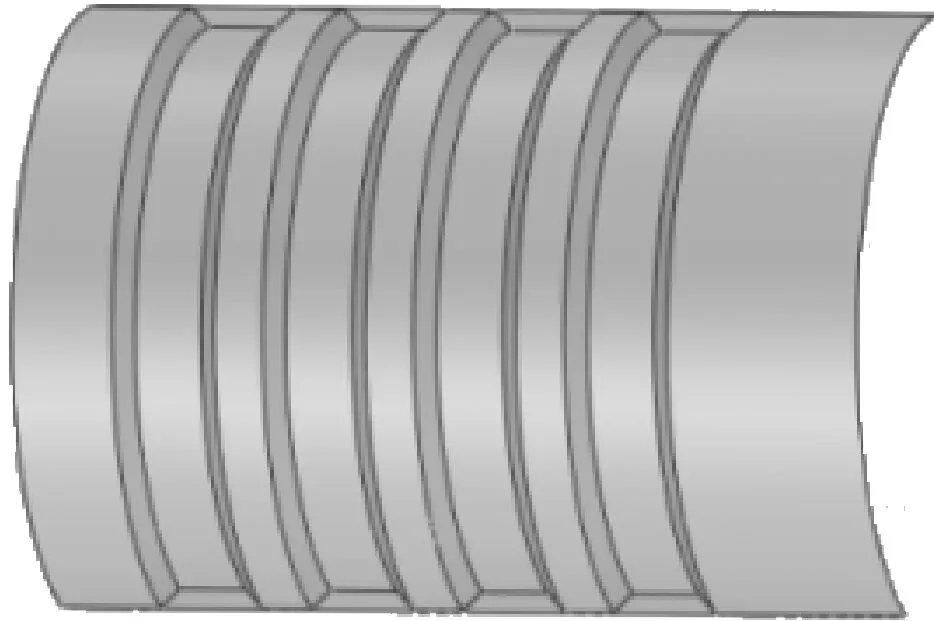
(a)原阀芯间隙的全剖视图

2.2 网格划分

利用Hypermesh对间隙模型进行网格划分。为了使计算结果更精确同时减少计算量，划分网格时，对开有导流槽的部位进行局部细化。划分网格的最小尺寸为0.02 mm，最大单元尺寸为0.32 mm，网格划分的结果如图5所示。

图5 插装阀阀芯网格划分Fig.5 Cartridge valve spool meshing

2.3 仿真分析设置

将划分好的网格模型导入fluent进行分析设置，设置进口、出口、内壁、外壁四种结构，设置进口压力分别为8 MPa、12 MPa，出口压力设置为0.1 MPa，介质为46号耐磨液压油，密度为889 kg/m3，运动粘度0.046 Pa·s，液压油流动状态为层流，不可压缩流体。添加数据监视器，对间隙液压油压力、切线应力进行监测。

3 CFD仿真结果分析

仿真结束后，提取相关数据，对数据进行处理。图6为原阀芯和新型阀芯间隙压力云图，图7为压力—间隙位置变化曲线，图8为切线应力—间隙位置变化曲线。从图7可以看出，新型阀芯间隙的压力变化情况：当入口压力为12 MPa时，在0～8 mm区间，压力从12 MPa近似线性下降到7.19 MPa；在8～42 mm区间，压力保持7.19 MPa；在42～56 mm区间，压力从7.19 MPa近似线性下降到0.1 MPa。当入口压力为8 MPa时，在0～8 mm区间，在压力从8 MPa近似线性下降到4.81 MPa；在8～42 mm区间，压力保持4.81 MPa；在42～56 mm区间，压力从4.81 MPa近似线性下降到0.1 MPa，这与理论分析结果相同。原阀芯的间隙的压力变化情况：在0～56 mm区间，当入口压力为12 MPa，压力从12 MPa呈现阶梯性下降，最终降为0.1 MPa；当入口压力为8 MPa，压力从8 MPa 呈现阶梯性下降，最终降为0.1 MPa。在阀芯上开均压槽和导流槽部分的压力基本上保持直线状态，原因是导流槽和均压槽的深度远大于间隙的大小，导流槽可以使均压槽间的压力相互关联，使压力分布更加均匀。

根据牛顿内摩擦定律分析阀芯与阀套间的切线应力是由于间隙内的压差引起的。由图8可知，新型阀芯间隙的切线应力变化情况：当入口压力为12 MPa时，间隙在0～8 mm区间，切线应力从14 950 Pa近似线性上升到15 800 Pa；在8～42 mm区间，除均压槽区域，切线应力保持在4 200 Pa上下波动；在42～56 mm区间，切线应力上升到13 700 Pa。当入口压力为8 MPa，间隙在0～8 mm区间，切线应力从10 100 Pa近似线性上升到11 000 Pa；在8～42 mm区间，除均压槽区域，切线应力保持在3 000 Pa上下波动；在42～56 mm区间，切线应力上升到9 500 Pa，并且新型阀芯间隙内的切线应力的波动范围较小。原阀芯的间隙切线应力变化情况：当入口压力为12 MPa，间隙在0～56 mm区间，除均压槽区域，切线应力在12 000 Pa上下波动，且波动范围较大。当入口压力为8 MPa，间隙在0～56 mm区间，除均压槽区域，切线应力在7 200 Pa 上下波动，且波动范围较大。新型阀芯在阀套内的受力更平稳，引起的磨损更小。因此使用新型阀芯可以延长插装阀的工作时间。

(a)原阀芯间隙入口压力8 MPa压力分布云图

(a)原阀芯间隙压力—间隙位置曲线

(a)原阀芯间隙切线应力—间隙位置曲线

4 结论

本研究对插装阀进行改进，增加了导流槽和柱形槽，并基于纳维斯托克斯方程、伯努利方程和阀芯卡紧力方程进行数学分析，通过计算机对原阀芯和新型阀芯间隙进行仿真分析。对两种结构的分析结果进行比较，结论如下。

1)新型阀芯间隙的压力变化为：在0～56 mm区间，当入口压力为12 MPa时，压力从12 MPa下降到0.1 MPa，变化曲线呈单阶梯下降；当入口压力为8 MPa时，压力从8 MPa下降到0.1 MPa，变化曲线呈单阶梯下降，这种下降趋势与理论分析结果相同。原阀芯间隙的压力变化为：间隙在0～56 mm区间，当入口压力为12 MPa时，压力从12 MPa呈现多阶梯下降到0.1 MPa；当入口压力为8 MPa时，压力从8 MPa呈现多阶梯下降到0.1 MPa。原因是导流槽和均压槽的深度远大于间隙的大小，导流槽可以使均压槽间的压力相互关联，使带有均压槽区域的压强分布相对均匀。

2)新型阀芯间隙的切线应力与原阀芯间隙的切线应力相比：除均压槽区域，原阀芯间隙的切线应力波动范围较大，而且在开导流槽区间受到切线应力远大于新型阀芯。新型阀芯在阀套内的受力更平稳，引起的磨损更小。