大蒜仿形浮动切根机构运动特性分析与仿真*

于昭洋，胡志超，杨明金，杨柯，彭宝良，张延化

(1.农业农村部南京农业机械化研究所，南京市，210014；2.西南大学工程技术学院，重庆市，400715)

0 引言

大蒜是我国最具国际竞争力的农作物之一，常年种植面积、总产量、出口量均居世界第1位[1-3]。我国大蒜以人工收获为主，人工收获大蒜需要完成挖掘、切秧、切根、收集装袋等多道工序，劳动强度大、作业效率低[4-5]。随着农村劳动力的进一步短缺，大蒜收获季用工荒现象凸显，人工收获雇佣费已高达26 980元/hm2，严重制约了蒜农种植积极性，产区对高效大蒜机械化收获技术装备的需求十分迫切。

由于我国大蒜种植土壤类型多样、品种繁杂，多采用覆膜种植，收获期易倒伏，鳞茎脆嫩易产生机械损伤，因而实现大蒜的机械化收获难度较大，2020年我国大蒜收获机械化水平不足3%[6-7]。近年来在市场需求和政策拉动双重驱动下，大蒜机械化收获进入快速发展期，国内科研单位相继研发出多种分段收获设备[8]和多行联合收获样机[9]。目前，我国部分地区已开始使用大蒜挖掘机[10-11]；多行高效联合收获设备仍处于优化提升和示范推广阶段。

我国已在大蒜联合收获挖掘起秧、夹持输送、切秧、清杂、集果等作业环节开展了多年持续攻关[12-15]，各环节技术水平逐渐趋于成熟。与之相比，有关大蒜联合收获切根技术的研发投入较少，发展相对滞后，已研发出的各类大蒜联合收获样机均无切根工序[16]。目前，我国现有大蒜联合收获切根技术研究多以理论分析和台架试验为主。赵丽清等[17]运用数字图像处理技术，研发了大蒜根脐线定位的专用算法，并运用GUI编程开发了大蒜根脐线自动、精确定位系统，为融合图像识别技术开展大蒜机械化切根技术研究提供了理论基础。胡志超等[18-19]提出了鳞茎仿形浮动切根方法，设计出滚筒螺旋均布式切割刀组，并开展了大蒜浮动切根作业机理分析和机构参数优化设计。蔡双雷[20]依据鳞茎根盘类圆锥体式几何特征，设计了U型刀片咬合式切割机构，开展了切割机构运动学特性研究，确定了切割机构关键结构参数。

本文以作者前期研发的一种大蒜联合收获仿形浮动切根机构[19]为研究对象，开展切根机构的运动特性分析与仿真试验，探索切根机构结构参数和运动参数对仿形浮动切根作业过程的影响，以期为大蒜联合收获仿形浮动切根作业机理研究和机构优化提供理论参考。

1 结构及工作原理

仿形浮动切根机构结构如图1所示，主要有夹持链、对齐链、对辊毛刷、固定式前旋转切刀、浮动式切割组件。作业时，夹持链和对齐链共同夹持蒜株茎秆向后输送，对辊毛刷清理根系粘附的泥土并将杂乱的根系捋顺；固定式前旋转切刀高速旋切，去除部分较长根系，完成根系预切；蒜株在夹持链上拉作用下，鳞茎逐渐靠近对齐链，完成鳞茎顶部对齐；随后，浮动式切割组件紧贴鳞茎底部仿形浮动，去除剩余全部根系。

图1 仿形浮动切根机构结构图Fig.1 Structure diagram of garlic root profiling floating cutting mechanism1.浮动式切割组件 2.夹持链 3.蒜株 4.对齐链 5.对辊毛刷 6.固定式前旋转切刀 7.拉伸弹簧

2 仿形浮动过程理论分析

2.1 仿形浮动过程解析

仿形浮动过程中鳞茎与浮动式切割组件相对位置关系如图2所示。图2(a)为鳞茎与浮动式切割组件接触后，向下浮动的初始时刻，即浮动初始时刻；图2(b)为浮动式切割组件位于鳞茎正下方，处于浮动最低点时刻，即浮动最低时刻；图2(c)为根系完成切割后，鳞茎即将与浮动式切割组件脱离接触时刻，即浮动结束时刻。

鳞茎在完成顶部对齐后，运动的鳞茎首先与浮动式切割组件的螺旋防护栅接触并发生弹性碰撞，鳞茎产生微小弹性形变，螺旋防护栅在拉伸弹簧作用下始终紧贴鳞茎底部；随后，螺旋防护栅在鳞茎底部施加的挤压力Fn和摩擦力Ft的共同作用下，向下浮动并顺时针转动，如图2(a)所示；当螺旋防护栅运动至鳞茎正下方时，浮动式切割组件向下浮动至最低点，拉伸弹簧达到最大伸长量，此时，螺旋防护栅受到的挤压力Fn达到最大值，如图2(b)所示；随后，鳞茎继续向后输送，螺旋防护栅紧贴鳞茎底部逐渐向上浮动，拉伸弹簧伸长量逐渐减小，螺旋防护栅受到的挤压力Fn逐渐减小，直至鳞茎与螺旋防护栅脱离接触，如图2(c)所示。

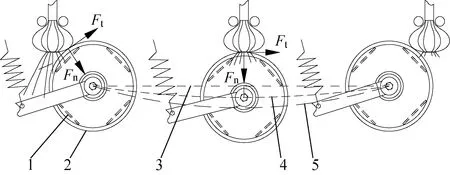
(a)浮动初始时刻 (b)浮动最低时刻 (c)浮动结束时刻图2 鳞茎与浮动式切割组件相对位置Fig.2 Relative position of garlic bulb and floating cutting assembly1.内置回转切刀 2.螺旋防护栅 3.相对运动轨迹① 4.相对运动轨迹② 5.相对运动轨迹③注：Fn、Ft分别为螺旋防护栅受到鳞茎底部施加的挤压力和摩擦力，N。

通过上述分析可知，仿形浮动过程中，浮动式切割组件先向下浮动，后向上浮动，在鳞茎实现顶部对齐后，浮动式切割组件浮动位移量与当前处理的鳞茎几何外形尺寸大小有关。当鳞茎较小时，浮动式切割组件相对鳞茎的运动轨迹近似直线，图2中运动轨迹①，此时，浮动式切割组件浮动位移量较小；当鳞茎较大时，浮动式切割组件相对鳞茎的运动轨迹为下凹弧线，图2中运动轨迹③，此时，浮动式切割组件浮动位移量较大。

2.2 浮动位移量建模

以浮动式切割组件浮动铰接点o为坐标原点，对齐链输送方向为x轴，竖直向上为y轴，建立平面定坐标系xoy。为便于分析，将鳞茎近似看作球体，以球体几何中心o′为坐标原点，对齐链输送方向为x′轴，竖直向上为y′轴，建立鳞茎平面动坐标系x′o′y′。浮动初始时刻，球体几何中心o′的坐标为(xo′，yo′)。则鳞茎外圆方程

(x-xo′)2+(y-yo′)2=r2

(1)

以螺旋防护栅几何中心c(xc，yc)为圆心，建立螺旋防护栅外圆方程

(x-xc)2+(y-yc)2=R2

(2)

式中：r——鳞茎外圆半径，m；

R——螺旋防护栅外圆半径，m。

为便于分析，忽略鳞茎与螺旋防护栅接触瞬间其自身的微小形变，认为鳞茎与螺旋防护栅接触初始时刻即为浮动初始时刻，此时，鳞茎外圆与螺旋防护栅外圆相切，由图3可得鳞茎球体几何中心o′与螺旋防护栅几何中心c的相对位置关系，如式(3)所示。

图3 浮动式切割组件浮动位移量建模示意图Fig.3 Schematic diagram of floating displacement modeling of floating cutting assembly

(3)

式中：h——浮动式切割组件浮动铰接点o到对齐链的距离，m；

l1——鳞茎球体几何中心o′到对齐链的距离，m。

由式(3)可得浮动初始时刻鳞茎球体几何中心o′(xo′，yo′)坐标

(4)

浮动初始时刻，鳞茎球体几何中心o′与螺旋防护栅外圆几何中心c连线o′c的斜率

(5)

当螺旋防护栅运动至鳞茎正下方时，浮动式切割组件向下浮动至最低点，浮动位移量达l最大值，由图3位置关系可得

l=lm+ln

(6)

(7)

(8)

式中：lm——鳞茎外圆与螺旋防护栅外圆相切点到根盘y向距离，m；

ln——鳞茎外圆与螺旋防护栅外圆相切点到螺旋防护栅外圆最高点的y向距离，m。

联立式(4)～式(8)可得

l=R+r-h+l1+yc

(9)

由式(9)可知，浮动式切割组件浮动位移量l与鳞茎外圆半径r、螺旋防护栅外圆半径R、鳞茎球体几何中心o′到对齐链的距离l1，螺旋防护栅几何中心点c的纵坐标yc等正相关，与浮动式切割组件浮动铰接点o到对齐链的距离h负相关。

通过上述分析，探明了浮动式切割组件的浮动位移量变化规律，并可通过式(9)精确计算出仿形浮动过程中浮动式切割组件的浮动位移量，可为拉伸弹簧的最大伸长量和预紧力设计、浮动式切割组件结构参数设计及其运动特性分析提供理论依据。

3 回转切刀运动学建模

3.1 切刀刃口轨迹曲面数学模型

浮动式切割组件内置回转切刀，回转切刀高速旋转将嵌入的根系切割。回转切刀的结构如图4所示，直刃切刀倾斜的安装在底座上，切刀与回转轴线的倾斜角度为α。

图4 回转切刀结构及轨迹曲线示意图Fig.4 Schematic diagram of rotary cutter structure and trajectory curve1.刃口轨迹曲线1 2.刃口轨迹曲线2 3.刃口轨迹曲线3

由于切刀为倾斜安装，其刃口的回转轨迹并不是圆柱面，刃口中点处的刃口回转半径最小，距离刃口中点越远处的刃口回转半径越大。刃口的回转轨迹为内凹曲面体，当进行根系浮动切割时，刃口中点处距鳞茎较远，刃口两端点处距鳞茎较近，从而形成鳞茎球体仿形切割，有效降低切割损伤、提高切净率。因此，有必要对切刀刃口的回转轨迹进行数学建模分析，以获取最佳仿形切割效果。

如图4所示，以内置回转切刀旋转轴线中点o为坐标原点，建立o-xyz空间直角坐标系。切刀刃口上任一点i在xoy平面中的坐标为(xi，d),则点i处切刀刃口回转半径

(10)

式中：xi——点i在x轴上横坐标值，mm；

α——切刀倾斜角度，(°)；

d——旋转轴线到切刀所在平面的距离，mm。

为建立切刀刃口在xoy平面内的轨迹曲线方程，将切刀刃口回转半径的值看作y坐标值，xi看作x坐标值，则由式(10)可得

(11)

则切刀刃口在xoy平面内的轨迹曲线方程

(12)

由式(12)可知，切刀刃口在xoy平面内的轨迹曲线为双曲线，因此，在o-xyz空间直角坐标系内，切刀旋转所形成的刃口轨迹曲面为旋转双曲面，由式(12)及旋转双曲面标准方程，即可求得则切刀刃口轨迹曲面方程

(13)

由式(13)可知，切刀刃口轨迹曲面与旋转轴线到切刀所在平面的距离d和切刀倾斜角度α有关，d越大则其轨迹曲面最小回转半径越大；α越大则其轨迹曲面在中心横截面(xoy平面)上轨迹曲线的曲率越大，曲线的弯曲程度越大。图4中，刃口轨迹曲线1对应的切刀倾斜角度α较大，刃口轨迹曲线3对应的切刀倾斜角度α较小。为保证根系完全切割，刃口轨迹曲线1极易造成鳞茎切伤，刃口轨迹曲线3的理论根系切净率小于刃口轨迹曲线2。因此，在回转切刀设计时，应根据大蒜鳞茎下球面几何特征统计结果，合理配置切刀倾斜角度α，使刃口轨迹曲线接近鳞茎下球面剖切面曲线，形成切刀刃口轨迹曲面对鳞茎下球面仿形切割。

3.2 刃口切割速度分析

如图5所示，作业时，蒜株由夹持链和对齐链的共同夹持作用下以恒定速度ve向后输送，回转切刀以恒定转速n高速旋切，切刀旋转方向与蒜株输送方向相反。由3.1节分析可知，切刀刃口不同位置处的刃口回转半径Ri不同，因而其旋转线速度vs不同。切刀刃口不同位置处的刃口旋转线速度

(14)

由式(14)可知，刃口旋转线速度vs不仅与切刀转速n、旋转轴线到切刀所在平面的距离d有关，还与切刀倾斜角度α、切刀刃口某一点处在x轴上横坐标值xi有关；切刀倾斜角度α越大，刃口旋转线速度vs越大；切刀刃口中点处的刃口旋转线速度vs最小，距离切刀刃口中点越远处的刃口旋转线速度vs越大。

设某一切刀所在平面转动至与水平面平行时为转动初始时刻，由图5可知，t时刻切刀转动的角度

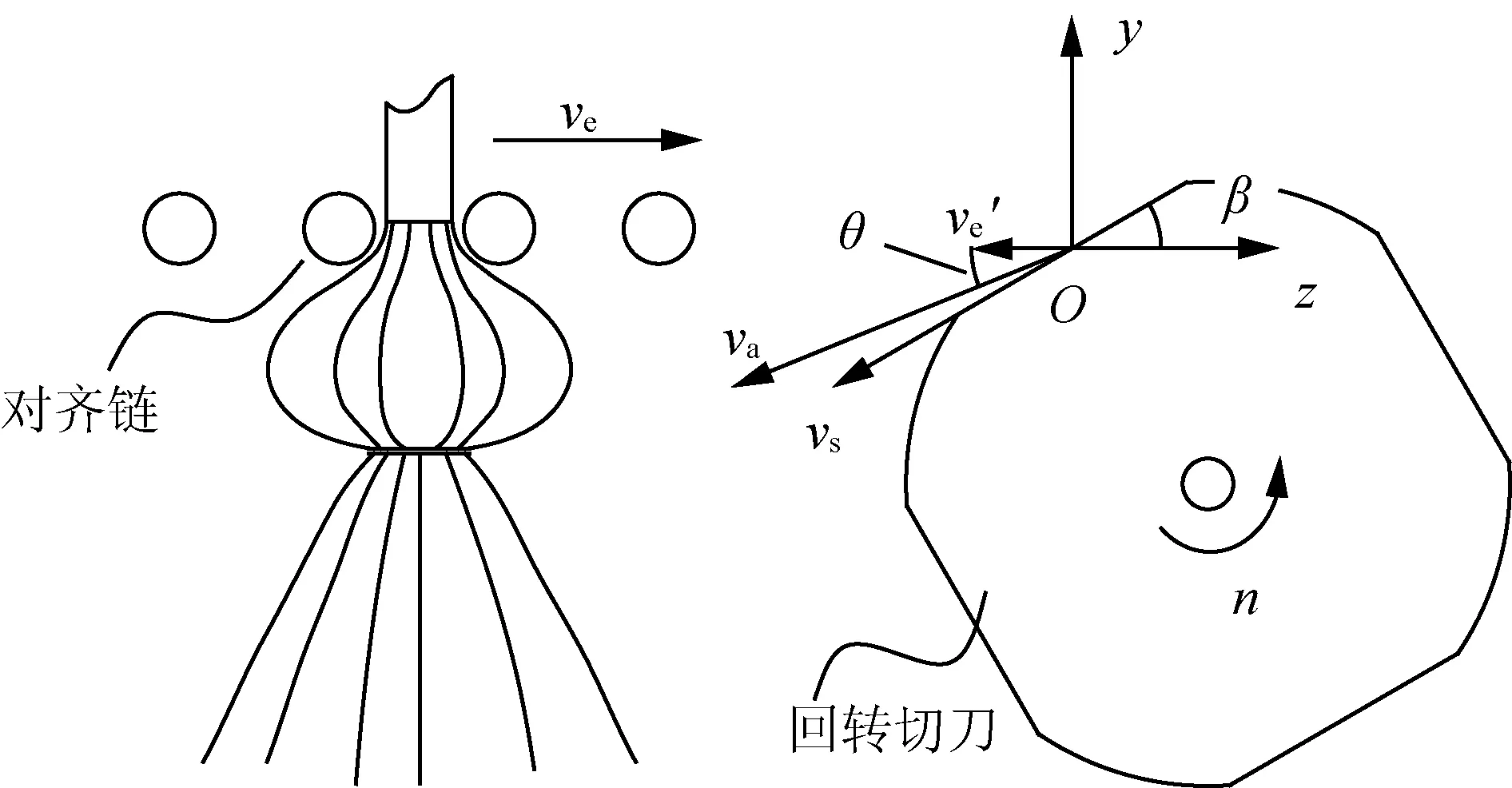
图5 回转切刀刃口切割速度分析Fig.5 Cutting speed analysis of the rotary cutter blade

(15)

式中：t——切刀转动时间，s；

n——切刀转速，r/min；

β——t时刻切刀转动的角度，rad。

本文只分析切刀转动第一周的速度变化情况，β取值范围[0，π/2]、[3π/2，2π]，此范围内为切刀对根系有效切割区。

将蒜株看作静止，则切刀刃口切割速度va为刃口旋转线速度vs与蒜株输送反向速度ve′的合成，求得va的大小和方向角为

(16)

(17)

式中：θ——va与水平面的夹角，rad。

由式(16)可知，切割过程中，刃口切割速度va的大小和方向均是不断变化的，即当刃口旋转线速度vs和蒜株输送反向速度ve′的大小都恒定不变时，刃口某一点的切割速度va大小和方向也是在不断变化的。当刃口某一点旋转至最高点时，切割速度va达到最大值；当刃口某一点旋转至最低点时，该切割速度va达到最小值。因此，刃口旋转最高点处为最佳切割位置，刃口轨迹曲面的最上方母线为最佳切割刃口轨迹曲线，此时刃口可以最大切割速度作用于根系。

4 回转切刀运动仿真试验

实际作业过程中，回转切刀是切根的主要执行部件，回转切刀刃口经过的根系区域才会产生切割作用。通过回转切刀运动仿真试验可以获取切刀运动轨迹、时间—速度曲线、位移—速度曲线，验证前文运动学理论分析结果，并进一步明确回转切刀结构和运动参数对根系群切割效果的影响。本文利用ADAMS虚拟样机仿真技术，开展回转切刀运动仿真试验[21-22]。

4.1 模型建立

为便于分析，将蒜株看作静止，回转切刀相对根系的运动行为可看作绕自身转轴的旋转运动和相对蒜株运动反向直线运动。根据实际设计参数在inventor中建立回转切刀的简化三维模型，以.x_t文件格式保存并导入ADAMS虚拟样机仿真分析软件中进行仿真前处理设置。

回转切刀模型包括切刀及底座，具体结构参数为：旋转轴线到切刀所在平面的距离d为54 mm，切刀倾斜角度α为33°、切刀刃口长度100 mm。模型导入ADAMS后，首先对各部件施加约束，切刀与底座通过固定副(Fixed)连接，回转切刀绕自身转轴的旋转运动通过铰接副(Revolute)实现，相对蒜株运动反向直线运动通过移动副(Translational)实现，最后对所有运动副添加驱动并开展仿真试验。

4.2 不同切刀转速对切割次数、漏切区、切刀运动轨迹影响

以蒜株输送速度ve为1 m/s为例进行分析(蒜株仿真中为静止)，则仿真过程中设置回转切刀相对蒜株反向直线运动速度ve′为1 m/s，回转切刀转速n分别为1 000 r/min、1 800 r/min、2 600 r/min，运动初始时刻，将某一切刀所在平面水平放置即图5中β为0°，并将旋转轴线放置于仿真全局坐标系原点。利用ADAMS/postprocessor模块获取单个切刀刃口中点O处运动轨迹，如图6～图8所示。

由前文分析结果可知，当刃口中点旋转至最高点时，切割速度va最大。同时，当刃口中点旋转至最高点时，刃口能够紧贴根盘切割，切割后剩余根系最短。因此，根系被刃口旋转最高点的切割次数是影响根系切净率关键因素。当刃口旋转最高点时，刃口将作用于根盘处的根系，以根盘直径25 mm为例进行分析。由图6～图8可知，回转切刀转速n越高，根系被刃口旋转最高点切割次数越多。当回转切刀转速n为1 000 r/min、1 800 r/min时，根盘处的根系被单个切刀刃口旋转最高点的切割次数为1次；当回转切刀转速n为2 600 r/min 时，根盘处的根系被单个切刀刃口旋转最高点的切割次数为2次，可满足切根作业要求。

由图6～图8可知，刃口中点运动轨迹相互交错，运动轨迹上方至根盘会形成漏切区，回转切刀转速n越高漏切区面积越小。为避免漏切，提高切净率，应提高回转切刀转速n。由图8可知，当回转切刀转速n为2 600 r/min时，漏切区面积很小，可满足切根作业要求。

在图6～图8中，刃口中点运动轨迹的切线顺时针方向为刃口旋转线速度vs的方向，当刃口旋转线速度vs水平分量与蒜株运动方向同向时，刃口中点运动轨迹的曲率较小，切刀切割总路程(轨迹曲线的总弧长)也较小。当刃口旋转线速度vs水平分量与蒜株运动方向反向时，刃口中点运动轨迹的曲率较大，切刀切割总路程(轨迹曲线的总弧长)也较大。

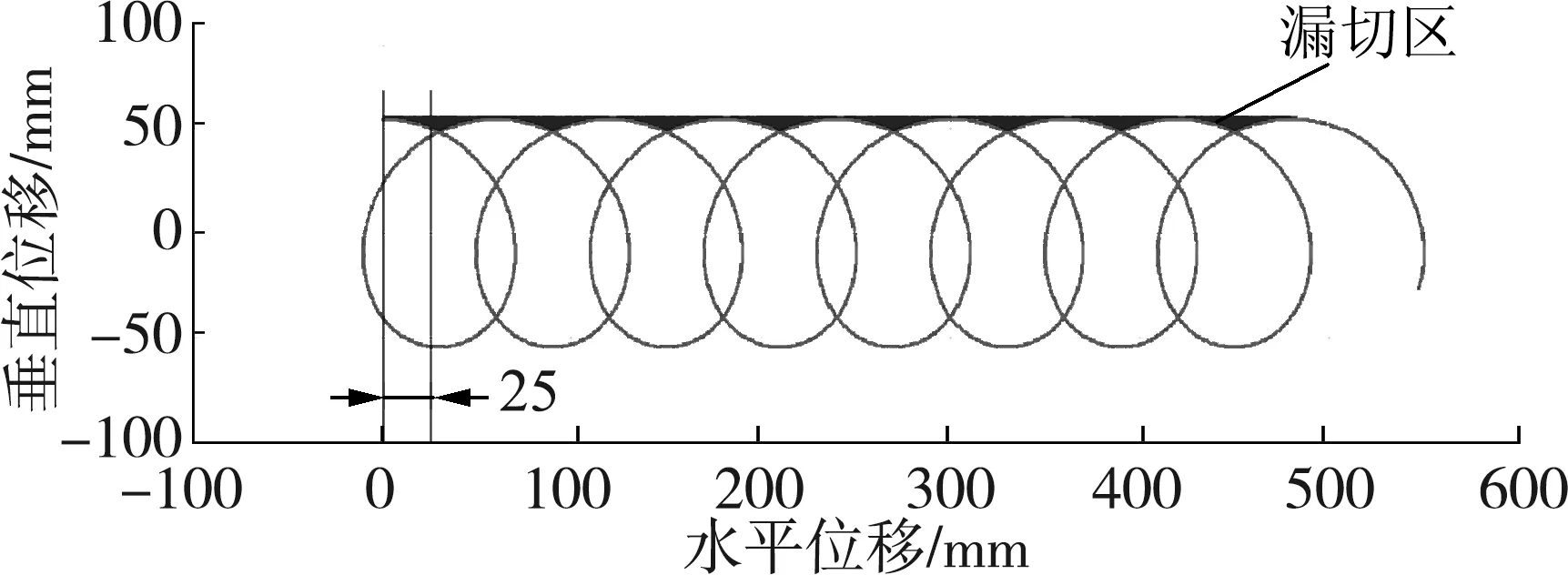
图6 切刀转速为1 000 r/min时刃口中点运动轨迹Fig.6 Motion trajectory of the cutter blade midpoint (Cutter rotational speed of 1 000 r/min)

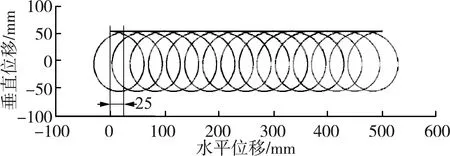
图7 切刀转速为1 800 r/min时刃口中点运动轨迹Fig.7 Motion trajectory of the cutter blade midpoint (Cutter rotational speed of 1 800 r/min)

图8 切刀转速为2 600 r/min时刃口中点运动轨迹Fig.8 Motion trajectory of the cutter blade midpoint (Cutter rotational speed of 2 600 r/min)

4.3 不同切刀数量对切割次数、漏切区、切刀运动轨迹的影响

为更加清晰、直观的分析后处理曲线图，以1 000 r/min的回转切刀转速为例进行分析，设置切刀数量分别为2片、4片且呈对称分布，其他参数设置同4.2节。利用ADAMS/postprocessor模块获取2片和4片切刀的刃口中点O处运动轨迹，如图9、图10所示。

图9 2片切刀刃口中点运动轨迹Fig.9 Motion trajectory of the cutter blade midpoint (2 pieces cutter)

图10 4片切刀刃口中点运动轨迹Fig.10 Motion trajectory of the cutter blade midpoint (4 pieces cutter)

由图9、图10可知，切刀数量越多，根系被刃口旋转最高点切割次数越多。当切刀数量为2片时，根盘处的根系被刃口旋转最高点的切割次数为1次；当切刀数量为4片时，根盘处的根系被刃口旋转最高点的切割次数为2次。

切刀数量越多，漏切区面积越小。为避免漏切，提高切净率，应提高切刀数量。由图10可知，切刀数量为4片时，漏切区面积很小，可以满足切割需求。

不同切刀运动初始位置不同，则其运动轨迹的初始点不同，但切刀运动轨迹变化趋势相同，因此，切刀数量对切刀刃口运动轨迹曲线没有影响。

4.4 同一刃口不同位置点处的切割速度

仿真参数设置同4.3节。利用ADAMS/postprocessor模块获取同一切刀刃口上，刃口中点处(点1)、距离中点20 mm处(点2)、距离中点40 mm处(点3)等不同位置点处的时间—速度曲线，如图11所示，图中速度为刃口切割速度va。

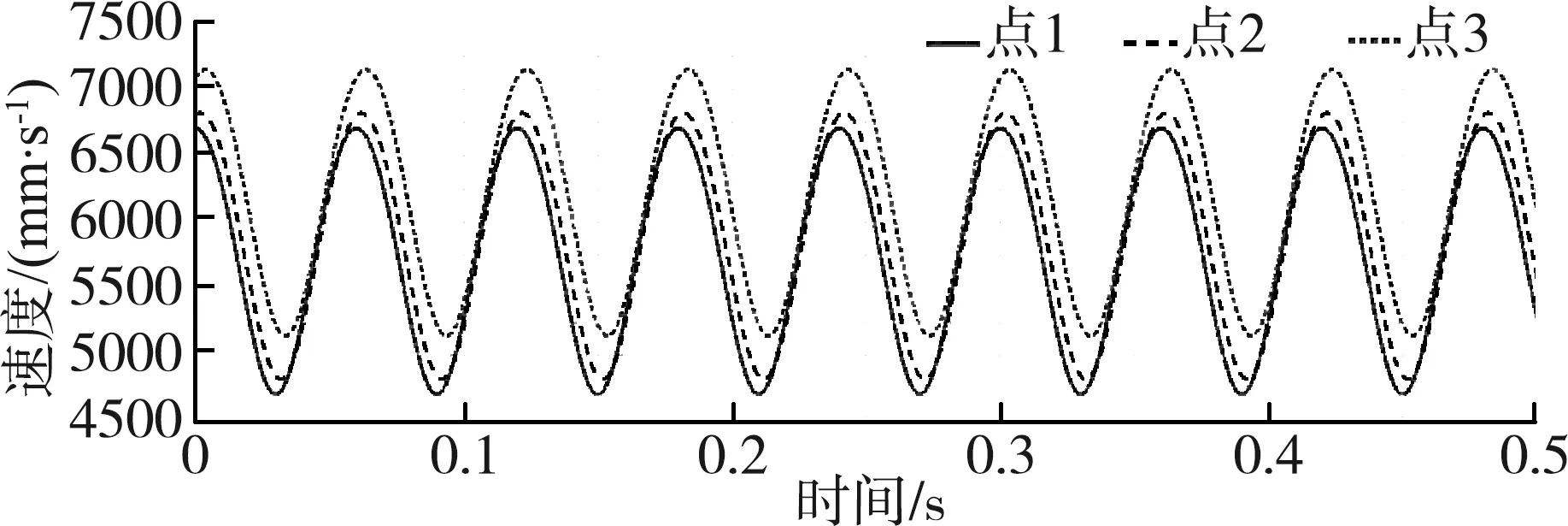
图11 时间—切割速度曲线Fig.11 Time-cutting speed curve

由图11可知，刃口中点处的切割速度va最小，距离刃口中点越远处的切割速度va越大，且随着距离的增加，切割速度增加幅度的更大。此外，同一切刀刃口上，刃口不同位置处到达切割速度最大值的时间不同。由于刃口中点处的切割速度小于刃口其他点处的切割速度，因此，在回转切刀运动参数理论设计时，应首先保证切割速度最小点处(即刃口中点)的切割速度达到根系切割要求。

4.5 切刀位移与切割速度关系

仿真参数设置同4.3节。利用ADAMS/postprocessor模块获取切刀的刃口中点O处水平位移—速度曲线、垂直位移—速度曲线，如图12、图13所示，图中速度为刃口切割速度va。

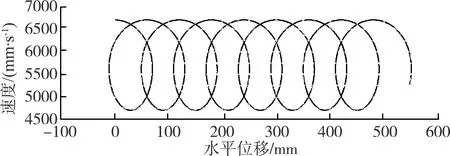
图12 切刀水平位移—切割速度曲线Fig.12 Horizontal displacement of cutter-cutting speed curve

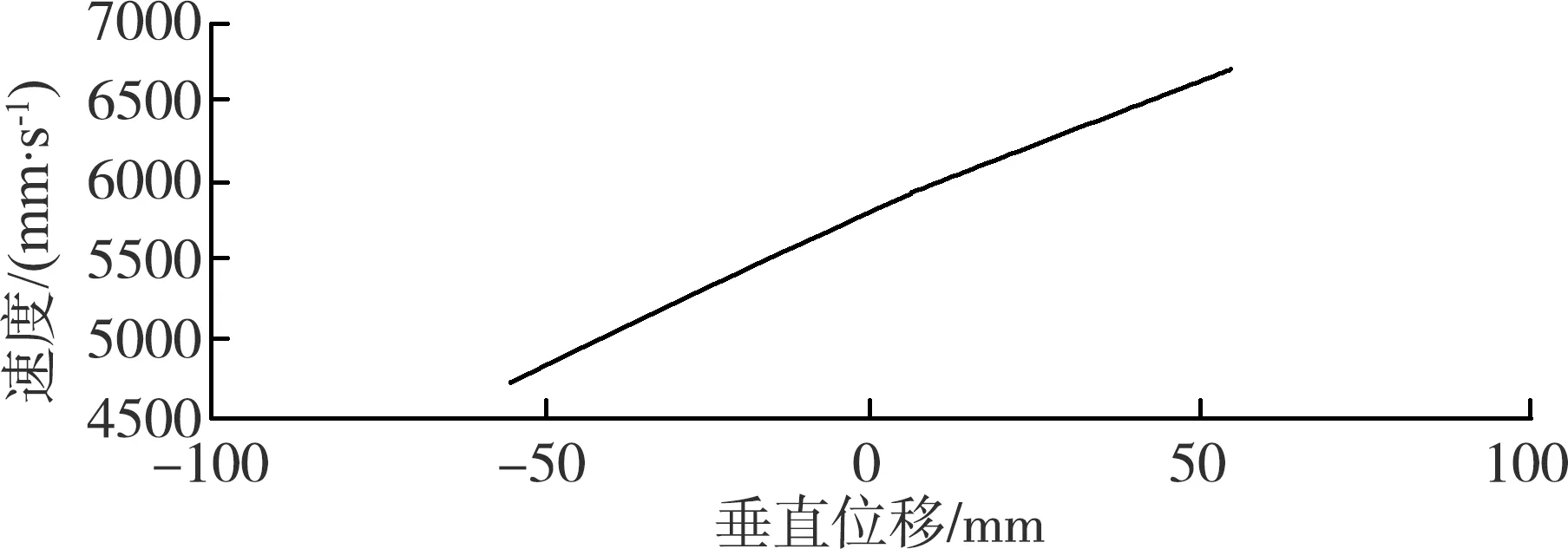
图13 切刀垂直位移—切割速度曲线Fig.13 Vertical displacement of cutter-cutting speed curve

如图12所示，切割速度与切刀水平位移呈螺旋性变化。水平位移—速度曲线可分为四个阶段分析，第一阶段为回转切刀转动角度为0～90°时，切割速度va随水平位移的增加而减小；第二阶段为回转切刀转动角度为90°～180°时，切割速度va随水平位移的减小而减小；第三阶段为回转切刀转动角度为180°～270°时，切割速度va随水平位移的减小而增加；第四阶段为回转切刀转动角度为270°～360°时，切割速度va随水平位移的增加而增加。

由图13可知，切割速度va与垂直位移近似于线性正相关；当刃口某一点旋转至最高点时，切割速度va达到最大值；当刃口某一点旋转至最低点时，该切割速度va达到最小值。在切割过程中，由于切刀自身回转作用，其垂直位移为最大和最小值之间往复循环，其切割速度va同样在最大和最小值之间往复循环。

5 结论

1)开展大蒜切根机构仿形浮动过程运动学解析，构建浮动式切割组件的浮动位移量数学模型，探明浮动位移量变化规律及其影响因素。浮动式切割组件浮动位移量与鳞茎外圆半径、螺旋防护栅外圆半径、鳞茎球体几何中心到对齐链的距离，螺旋防护栅几何中心点的垂直方向坐标等正相关，与浮动铰接点到对齐链的距离负相关。

2)构建切刀刃口轨迹曲面数学模型，明确切刀旋转所形成的刃口轨迹曲面为旋转双曲面，同时，切刀倾斜角度决定了旋转双曲面在中心横截面上轨迹曲线的曲率和弯曲程度，倾斜角度越大则其轨迹曲线的曲率越大、弯曲程度越大。通过合理配置切刀倾斜角度，该回转切刀可形成针对鳞茎下球面弧形的仿形切割。

3)构建切刀刃口切割速度数学模型，确定刃口旋转最高点处为最佳切割位置，刃口轨迹曲面的最上方母线为最佳切割刃口轨迹曲线。此外，刃口同一点处的切割速度的大小和方向均是不断变化的。当刃口某一点旋转至最低点时，切割速度最小；当刃口某一点旋转至最高点时，切割速度最大，此时刃口可以最大切割速度作用于根系。

4)通过ADAMS虚拟样机仿真试验，获取切刀运动轨迹、时间—切割速度曲线、位移—切割速度曲线，由仿真分析结果可知：回转切刀转速越高、切刀数量越多，则切割次数越多、漏切区面积越小；当回转切刀转速为2 600 r/min或切刀数量为4片时，根盘处的根系被单个切刀刃口旋转最高点的切割次数可达到2次，且漏切区面积很小，可以忽略；刃口中点处的切割速度小于刃口其他点处的切割速度，运动参数设计应首先保证刃口中点的切割速度达到根系切割要求；切割速度与切刀水平位移呈螺旋性变化，切割速度与切刀垂直位移近似于线性正相关。