一种基于Voronoi_Obstacle场的移动机器人路径规划算法

庞风麟，骆敏舟, 3，柳 聪, 柏永华, 徐孝彬

(1.河海大学机电工程学院，江苏 常州 213022) (2.河海大学江苏省特种机器人技术重点实验室，江苏 常州 213022) (3.江苏集萃智能制造技术研究所有限公司， 江苏 南京 211800)

近年来，移动机器人广受社会各界关注，在工业、农业、服务、搜救等领域得到广泛应用[1]。路径规划作为智能移动机器人的关键技术之一，成为各个领域研究的热点[2-4]。

路径规划算法按照不同的工作需求，可分为路径最优算法、安全距离最优算法、能量最优算法等。其中路径最优算法主要包括A*算法、D*算法、Dijkstra算法、RRT算法、遗传算法、粒子群算法、Q-learning算法等[2-4]；安全距离最优算法主要包括人工势场法、Voronoi图算法等[2-4]；能量最优算法主要包括基于随机动态正交水平集的能量最优算法、基于改进A*算法的能耗最优路径规划等[5-6]。本文主要讨论安全距离最优算法。

Khatib[7]于1986年提出人工势场法(artificial potential field，APF)，该算法可规划一条避开障碍物的安全路径，但在计算过程中可能出现因引力势场和斥力势场相互抵消而陷入局部最小解的情况[8]。赵明等[9]提出了域-人工势场法，通过加入自适应的域势场，帮助移动机器人根据域势场快速到达目标点，避免陷入叠加势场带来的局部最小解。Fedorenko等[10]提出了基于Voronoi图的路径规划算法，通过生成的Voronoi图，得到一条最优安全路径，但其采用三段式广度优先搜索规划路径，计算时间长，无法满足实时计算的要求。任晓兵等[11]提出了使用Voronoi图的节点信息进行路径规划，减少了路径规划计算时间，但因计算Voronoi节点信息增加了计算负担，延长了规划时间，并且只使用节点信息，无法获得最优安全路径。Dolgov等[12]提出了基于Voronoi场的Hybrid A*算法，但Voronoi场计算复杂度高，计算时间长，难以满足实时计算的要求。

1 Voronoi_Obstacle场

Dolgov等[12]提出基于最近障碍物和最近Voronoi点信息构建Voronoi场。在二维空间，使用K-D树搜索最近障碍物和最近Voronoi点时，构建Voronoi场的复杂度为O(n2.5)，当机器人工作场景变大时，Voronoi场计算量变大，计算时间延长。本文采用分层多步骤[13]的思想，其层次结构如图1所示。

图1 层次结构

1.1 基于障碍物的势场

地图膨胀广泛应用于移动机器人导航，通过设置合适的膨胀值，可以规划出远离障碍物的安全路径, 降低碰撞的风险[13-15]。本文采用Lu等[13]提出的膨胀思想建立障碍物的势场，考虑移动机器人实际尺寸，势场公式如下：

(1)

式中：κx为距离障碍物的危险值，其会随着远离障碍物的方向逐渐趋向于0；x为配置空间中的点；X为机器人的配置空间；pob为x处最近的障碍物；d(x,pob)为x与pob的距离；Drodot为机器人的尺寸；μ为衰减率。

1.2 基于Voronoi图的势场

Voronoi图由俄国数学家格奥尔吉·沃罗诺伊提出，其将平面划分为基于特定点子集的子区域，其中特定点子集(称为种子)是预先指定的，并且每个种子所对应的子区域中任一点到该种子的距离要比到其他任何种子的距离近，Voronoi图的定义如下[16-17]：

Rk={x∈X|d(x,Pk)≤d(x,Pj) for all

j≠k}

(2)

式中：Rk为Voronoi区域；Pk，Pj为特定元组(种子)；d(x,Pk)为x到Pk的距离。

本文采用Lau等[18]提出的方法得到Voronoi图。与1.1节算法思想一致，本文采用膨胀思想对生成的Voronoi图建立Voronoi势场，Voronoi势场不考虑机器人的实际尺寸，势场公式如下：

χx=e-vd(x,pvo)x∈X

(3)

式中：χx∈[0,1)，表示距离Voronoi的程度值，其会随着远离Voronoi的方向逐渐趋向于0；pvo表示距离机器人最近的Voronoi点；d(x,pvo)为x到pvo的距离；v为增益率。

1.3 基于障碍物势场和Voronoi图势场的Voronoi_ Obstacle场

传统的Voronoi场的计算公式如下[12]：

(4)

传统Voronoi场的复杂度为O(n2.5)，其复杂度高，计算时间长。为解决此问题，本文提出采用分层多步骤的思想计算Voronoi_Obstacle场，计算公式如下：

(5)

式中：ρx为Voronoi_Obstacle场在x处的势场值，当κx≥κmax时，ρx为0，ρx会随着远离Voronoi的方向逐渐趋向于1；κmax为最大衰减值，是常量值。

式(5)不考虑最近障碍物和最近Voronoi点的距离，而是通过κx和χx计算Voronoi_Obstacle场。在二维空间，本文提出的Voronoi_Obstacle场的复杂度为O(n2)，复杂度降低O(n0.5)。

基于障碍物势场和Voronoi图势场的Voronoi_Obstacle场详细的分层结构如图2所示。

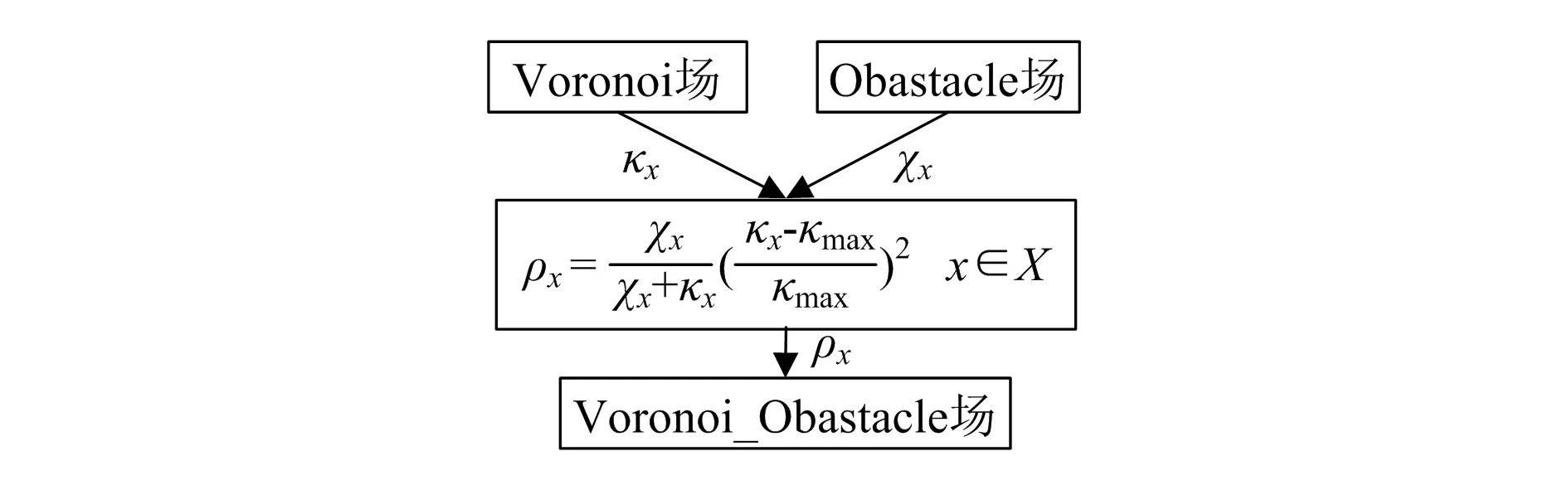
图2 Voronoi_Obstacle场的分层结构图

2 基于Voronoi_Obstacle场的启发式搜索算法

A*算法是一种典型的启发式搜索计算方法，其表达式如下：

f(n)=g(n)+h(n)

(6)

式中：f(n)为从起始点到目标点的估价函数；g(n)为从起始点到节点n的移动代价；h(n)为从节点n到目标节点估计代价，其表示启发式代价。

本文采用改进的A*算法对Voronoi_Obstacle场进行启发式搜索，在A*的基础上加入启发式权重值，可以人为更改启发值的权重，并且对g(n)和h(n)重新进行定义，表达式如下：

f(n)=g(n)+w·h(n)

(7)

(8)

(9)

式中：w为启发式权重值；ρi为配置空间i处的Voronoi场值；d(x,y)表示从x到y的距离。

其算法流程如图3所示，updateState()函数和Main()函数与传统的A*算法相同，此处不展开描述。

图3 算法流程图

3 实验分析

3.1 实验硬件配置及环境描述

3.1.1实验硬件配置描述

图4为自主研发的差速轮移动底盘，平台上装有惯性测量单元(inertial measurement unit, IMU)、轮式里程计、二维激光雷达等传感器。IMU采用三驰惯性公司的SC-AHRS-100D4，采集频率为100 Hz；二维激光雷达采用镭神智能系统有限公司的N301激光雷达，量程为30 m，采集频率为10 Hz；差速轮采用轮毂电机，编码器采集频率为50 Hz；工控机采用I7-7500U。

图4 差速轮移动底盘

3.1.2实验环境描述

为验证提出的基于Voronoi_Obstacle场的移动机器人路径规划算法的可行性及优越性，本文利用室内真实环境进行对比实验。实际场景(25 m×37 m)如图5所示，对环境进行二维地图构建，结果如图6所示，本文采用Lau等[18]提出的方法生成Voronoi图，结果如图7所示。

图5 实际场景

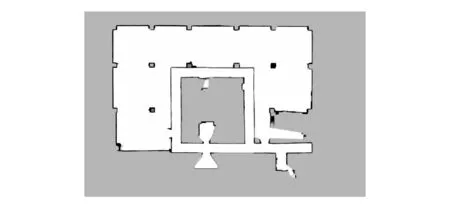
图6 构建的二维地图

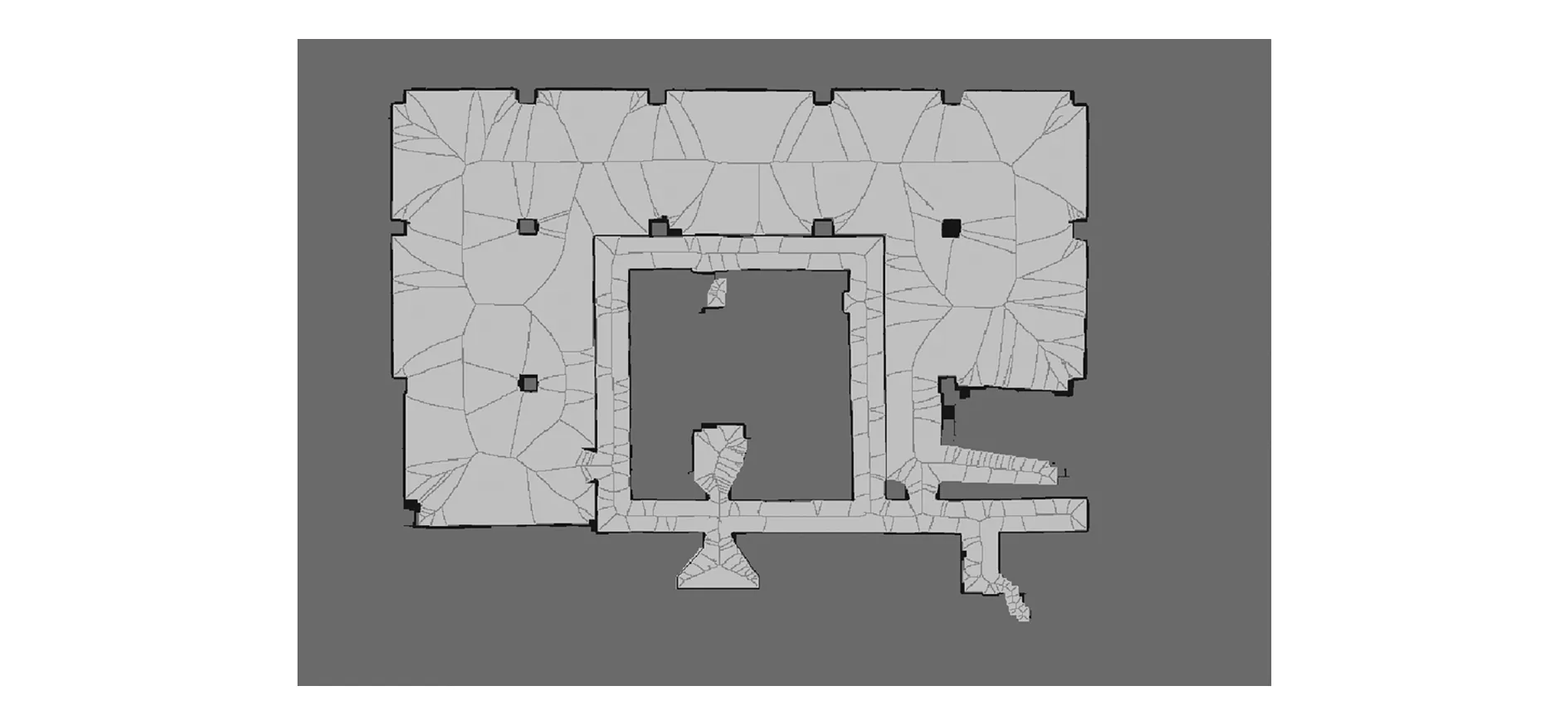
图7 基于二维地图的Voronoi图

3.2 实验结果对比分析

本文进行3组实验对比分析。

2)将传统的基于Voronoi图的路径规划算法[10]与基于Voronoi_Obstacle场的路径规划算法进行对比实验。采用图9中的Voronoi_Obstacle场进行路径规划，并设起点为(2.3，-7.5)、终点为(15.8，-31.0)。实验结果如图10，11所示，本文进行30次实验，并取平均值，基于Voronoi图的路径规划的平均时间为0.863 s，而基于Voronoi_Obstacle场的路径规划的平均时间为0.565 s，时间缩短34.53%，并得到一条安全距离路径，保证了机器人的安全运行。实验结果表明，所提出的基于Voronoi_Obstacle场的移动机器人路径规划算法具有一定的可行性和优越性。

图8 传统的Voronoi场图

图9 Voronoi_Obstacle场图

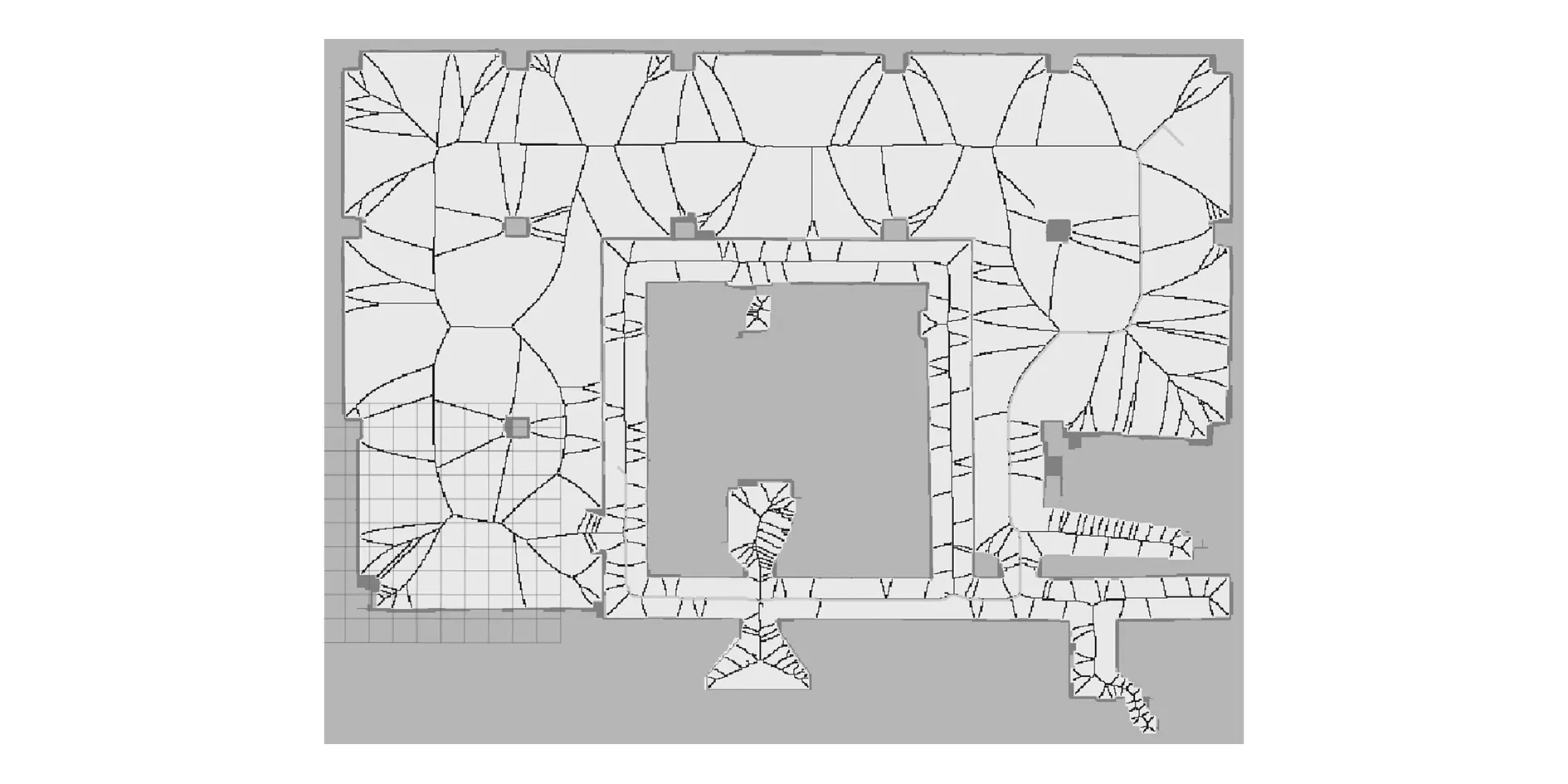
图10 传统基于Voronoi图的路径规划算法

图11 基于Voronoi_Obstacle场的路径规划算法

3)将改进的基于Voronoi图的路径规划[11]与本文提出的基于Voronoi_Obstacle场的路径规划算法进行对比实验。采用图9中的Voronoi_Obstacle场，并设起点为(2.3，-7.5)、终点为(15.8，-31.0)。实验结果如图12，13所示，本文进行30次实验，并取平均值，改进的基于Voronoi图的路径规划的平均时间为0.828 s，而基于Voronoi_Obstacle场的路径规划的平均时间为0.565 s，时间缩短31.76%。改进的基于Voronoi图的路径规划计算Voronoi节点信息时间为0.804 s，占据总规划时间的94.1%，表明计算Voronoi节点增加了计算负担，延长了规划时间，并且如图12中A、B所示，改进的基于Voronoi图的路径规划算法并未完全使用Voronoi点信息，只使用了Voronoi节点信息，其会产生一条伪最优或者次优的安全距离路径。

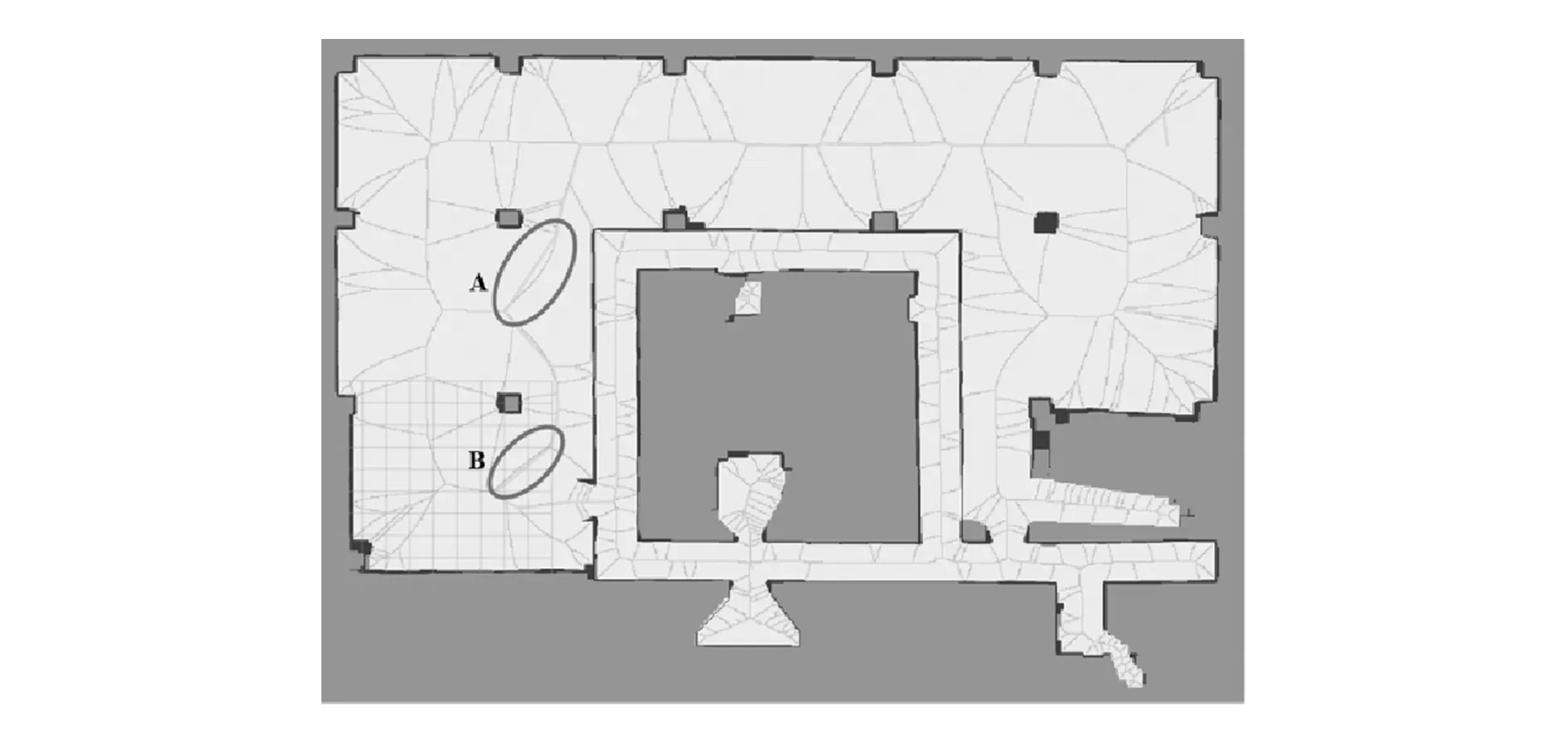
图12 改进的基于Voronoi图的路径规划算法

图13 基于Voronoi_Obstacle场的路径规划算法

4 结束语

本文研究了Voronoi场计算复杂和基于Voronoi图路径规划计算缓慢的问题。主要创新点是提出了一种基于Voronoi_Obstacle场的移动机器人路径规划算法，从而缩短生成Voronoi_Obstacle场和路径规划的计算时间。传统的基于Voronoi图的路径规划，在空间变大、毛刺增多、栅格密度变大等情况下，Voronoi信息增多，规划缓慢，并且传统的Voronoi场计算复杂度高，计算缓慢，本文利用基于改进的Voronoi_Obstacle场进行启发式搜索，大大减少了计算量，缩短了规划时间。该方法适用于移动机器人的路径规划，可提供可靠、实时、安全的导航路径。本文在实际室内环境进行了测试验证，通过3组实验对比，表明本文提出的基于Voronoi_Obstacle场的移动机器人路径规划算法具有一定的可行性和优越性。