系统维度对变密度溶质运移的影响研究
叶 逾 ,蔡芳敏 ,谢一凡 ,井 淼 ,鲁春辉
(1.河海大学水利水电学院,江苏 南京 210098;2.河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098;3.河海大学长江保护与绿色发展研究院,江苏 南京 210098)
地下含水层中常出现流体密度差,受重力作用驱动引发对流过程,形成物质传输[1-2]。常见的地下水密度差异主要来源于人类活动,如油田的卤水处理、垃圾填埋的渗滤、农业化肥的入渗、高密度水相工业溶液的灌入等[3-5]。除此之外,海水入侵也是常见的变密度流问题[6-7]。对流过程导致不稳定性的发生,增加溶质运移的不确定性,将显著提升地下水管理和修复的难度[8-9]。因此,正确量化对流及其作用下的溶质运移过程是预测含水层中污染物迁移的理论基础,对有效修复地下水具有重要意义。
仅在流体密度梯度驱动下的流动称为自由对流[10]。在自由对流过程中,处于上层的入侵溶液(高密度流体)由于重力作用变得不稳定,由密度梯度驱动入渗至低密度流体中,形成指流,从而增大流体间的混合,并最终形成稳定的密度梯度分布[11]。大量的室内试验和数值模拟研究表明,流体密度差、多孔介质渗透性和含水率是影响变密度流和溶质运移的关键因素[12-15]。其中,多孔介质的非均质性空间分布对于对流和溶质运移的影响更是成为了多年来的研究热点[16-17]。例如,Post等[18]通过砂槽试验和数值模拟研究了离散低渗透性结构对自由对流的影响,揭示了高渗透性区域的层内对流和低渗透性区域的层间对流两种不同机理;Kreyns等[19]研究了非均质连通性对海岸带含水层中的变密度流及溶质运移的影响,指出优先通道流作用于海岸带地下水的流动和溶质运移,使其混合带增大、盐度分布更加复杂。更复杂的研究包括Lu等[20]在自由对流过程中进一步考虑了多孔介质两区动力学传质过程,强调了两区动力学传质对于自由对流中溶质运移的重要影响;Xie等[21-22]研究了多孔介质中自由对流指流的速度及其不确定性,发现采用随机框架可以减小指流和流速的不确定性。
然而,由于数值计算量的庞大和试验操作的复杂性,关于地下水变密度流的研究基本限于二维系统,三维系统中的研究极少有被报道[23-25]。仅有零星研究表明,三维系统中的变密度流与二维系统不同,密度效应可能会因三维系统中更强的弥散效应而被减弱,但是也有可能导致更大尺寸的指流以及指流间的交汇[26-27]。目前,聚焦于系统维度对均质多孔介质中自由对流和溶质运移影响的研究还未见报道。本文通过数值模拟二维和三维系统中的自由对流和溶质运移,观测指流等不稳定性的产生和演变过程,量化不同维度下的溶质扩散和稀释程度,明确系统维度对自由对流和溶质运移的作用机制,以预防基于二维系统的计算结果对预测三维自然含水层中自由对流和溶质运移所产生的错误估计。
1 数值模拟
采用变密度地下水流与溶质运移程序SEAWAT-2000进行数值模拟,该程序耦合了MODFLOW-2000和MT3DMS两个子程序。
1.1 基本方程
多孔介质中的变密度地下水流控制方程为:
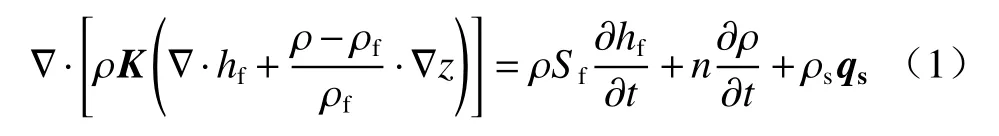
式中:K——渗透系数张量/(m·s-1);
z——垂向坐标/m;
hf——淡水水头当量/m;
ρ——流体密度/(kg·m-3);
ρf——淡水密度/(kg·m-3);
Sf——储水系数/m-1;
n——有效孔隙度;
t——时间/s;
ρs——源/汇项流体密度/(kg·m-3);
qs——源/汇项单位体积流量/s-1。
溶质运移采用传统的对流-弥散方程:

式中:c——溶质的浓度/(kg·m-3);
D——水动力弥散系数/(m2·s-1);
u——流体速度/(m·s-1)。
流体密度和浓度之间存在的经验关系为[28-29]:

式中:ε——密度对浓度的梯度。
1.2 数值模型
二维和三维数值模型设置见图1。二维模型改编自Elder problem经典自由对流模型,模拟区域长600 m、高150 m。三维模型的长和高与二维模型一致,其宽为100 m。长、宽、高分别用字母L、W和H来表示。二者均为均质多孔介质填充。为了避免网格剖分对数值模拟结果的影响[30],选择纵向(即x方向)离散间距为3 m,横向(即y方向)离散间距为1 m,垂向(即z方向)离散间距为1.5 m。二维和三维模型分别剖分20 000和2 000 000 个网格。模型的左、右边界顶部作为流体和溶质的出口,设置为定水头边界,其余左、右边界为不透水边界。模型底部为无流量边界,而顶部源区设为定浓度边界条件,浓度为280 kg/m3,对应密度1 200 kg/m3。在流体密度1 000~1 200 kg/m3范围内,ε值为0.714 3[31]。在二维模型中,源区长度(Ls)为300 m;三维模型中的源区长(Ls)为300 m,宽(Ws)为50 m。起初,模拟区域充满了淡水,一旦有足够多的溶质通过扩散从源区进入模型上边界后,将由密度驱动进入模型内部,直到整个区域充满与源区浓度相等的溶质,达到稳态分布。因此,模拟时间步长为1 d,总长设为50 a,此时已有大量溶质进入模拟区域并到达模型底部。模型其它参数设置见表1。
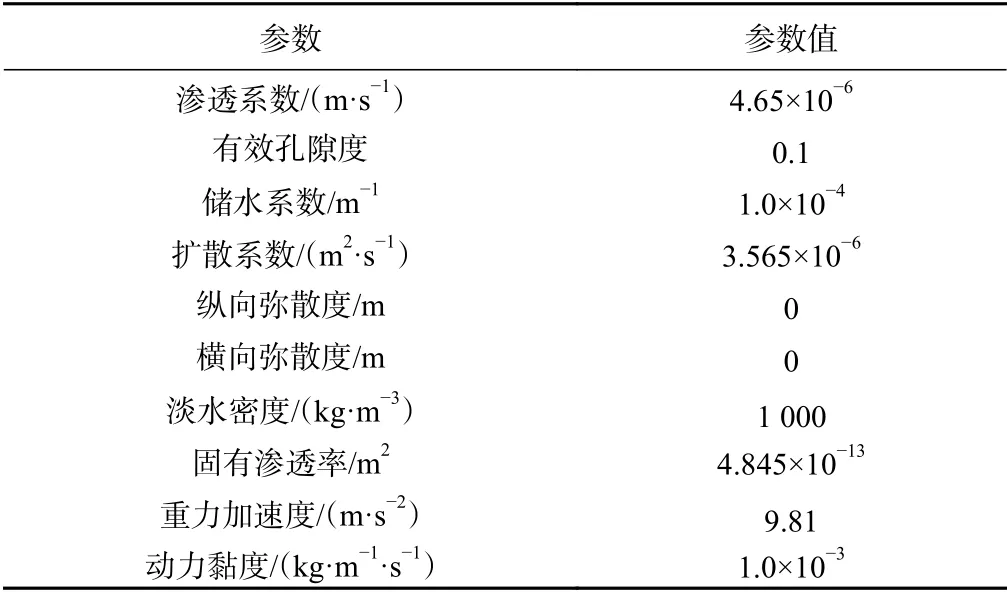
表1 模型中的参数值Table 1 Parameters used in the numerical model
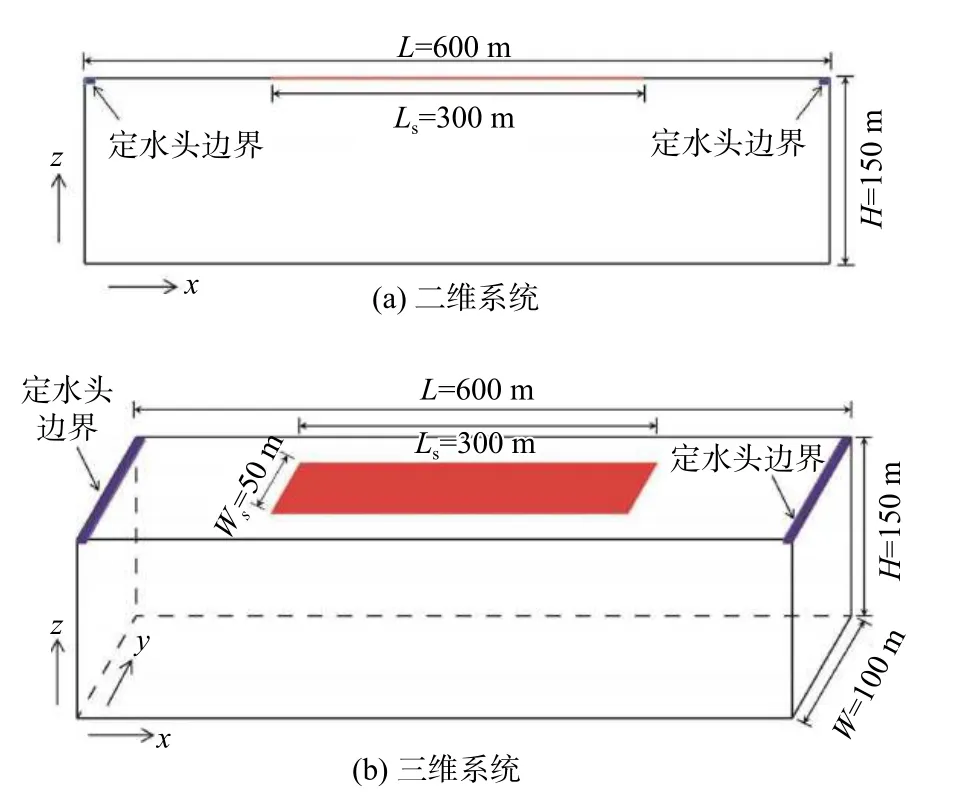
图1 数值模型设置图Fig.1 Sketch of the numerical model
1.3 量化参数
传统上采用无量纲瑞利数(Rayleigh number)来判断不稳定性的发生与否[16]。瑞利数被定义为密度驱
动力与扩散造成的阻力之间的比值,其计算公式为:

式中:k——固有渗透率/m2;
g——重力加速度/(m·s-2);
μ——动力黏度/(kg·m-1·s-1);
Dd——分子扩散系数/(m2·s-1);
α——相对密度比。
相对密度比α定义为:

另一个可用来判断系统稳定性的参数为舍伍德数(Sherwood number)。该参数被定义为自由对流造成的传质与扩散导致的传质之间的比值,其计算公式为:
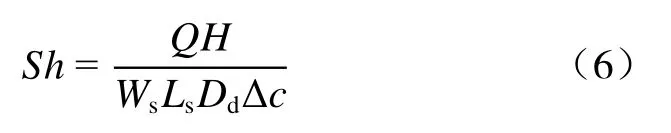
式中:Q——通过顶部边界的溶质质量通量/(kg·m2·s-1);
Ws——源区宽度/m;
Ls——源区长度/m;
Δc——源区溶液与淡水的最大浓度差/(kg·m-3)。
当Sh大于1时,系统由于对流和扩散过程呈现不稳定性;相反,当Sh值为1时,系统仅包含扩散运移,表现为稳定系统。
溶质在运移过程中的分布特征大多通过计算空间矩来衡量。零阶矩(m0)为区域内溶质的总质量,单位为kg;经零阶矩标准化后得到的空间一阶矩即为溶质羽的质心(x0),单位为m;而二阶中心矩(m2c)一般用来描述溶质羽围绕着质心的扩散情况,单位为m2;其计算公式分别为[32]:
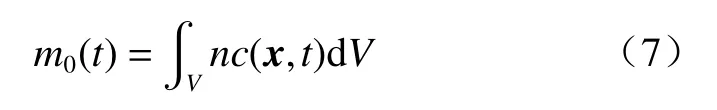
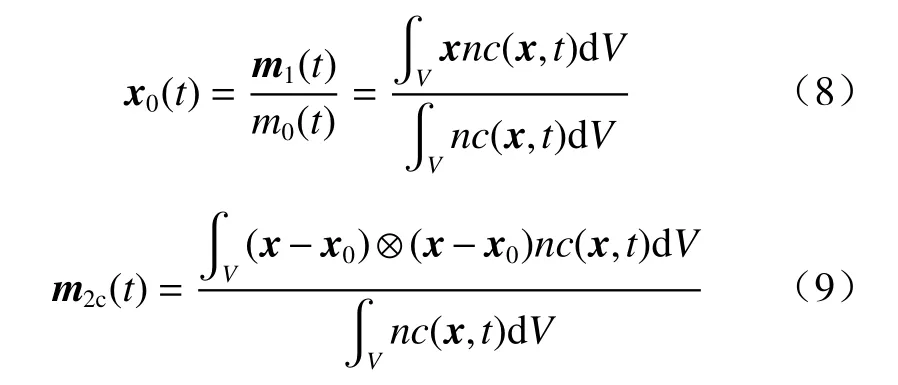
式中:x——在x、y、z方向上的空间坐标向量/m;
m1——一阶空间原始矩/(kg·m);
V——模拟区域,在三维系统中为体积/m3,在二维系统中为面积/m2;
值得注意的是,此处的x0和m2c均为矢量。本文采用溶质羽在z方向上的质心位置(z0)以及其在x、y、z三个空间方向上的二阶中心矩(m2c=(m2c,xx,m2c,yy,m2c,zz))来描述溶质羽的运移情况。
由于空间二阶矩量化的是溶质相对于质心扩散的程度,并非真正的稀释度,因此,本文同时通过计算稀释指数(E)来描述溶质通过对流弥散得到的稀释程度[32]。该参数计算了溶质空间分布的无序性,其值等于香农熵指数(Shannon entropy):

其中,p为粒子位置的概率分布,其定义为:
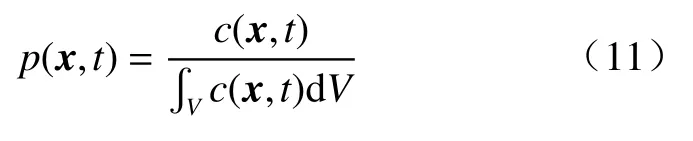
反应比率(reactor ratio,M)被定义为稀释指数值与其理论最大值(Emax)之间的比值[32],其公式为:

当溶质充满整个模拟区域,并且区域内浓度均一时,稀释达到理论最大值,其值为模拟区域的总体积。反应比率取值范围为0~1之间。
2 结果与讨论
2.1 对流与溶质分布
图2展示了第5年二维和三维中心截面上溶质羽的分布情况,图中的C为相对于源区的标准化浓度,无量纲。由图2(a)可见,二维系统中出现4条分散的指流,指流呈中心对称分布,中间2条指流较小,两侧的指流较大,表明两侧的不稳定性相对更强。指流边缘由于扩散作用表现出平滑的浓度梯度分布,两侧的指流则因扩散作用到达模拟区域底部。三维系统中溶质羽在x-z与y-z中心截面的分布分别见图2(b)和图2(c)。溶质羽在三维系统中同样呈中心对称分布。然而,与二维系统不同的是,整个系统中并未出现分散的指流,溶质羽成团下渗,仅在x-z截面的源区两侧表现出相对较高的浓度分布。二维和三维系统中溶质羽分布的显著差异表明了不同系统维度下自由对流和溶质扩散过程的区别,由于三维系统中的扩散程度较二维系统更大,可能抑制三维系统中指流的产生。

图2 第5年的溶质羽分布图Fig.2 Concentration distributions of the solute plume in the 5th year
图3展示了二维系统x-z截面和三维系统x-z中心截面上不同时间点的溶质羽分布。二维系统中的4条分散指流随着对流和扩散过程的进行逐渐交汇,10 a后演化为2条尺寸较大的分散指流, 20 a后指流已完全交汇,并且继续通过对流/扩散蔓延至系统整个区域。三维系统中溶质羽的发展和演化与二维系统截然不同。在整个模拟时间内,三维系统中未曾出现分散的指流,仅在部分区域表现出一些强不稳定性。例如,当t=4 a时,三维系统源区下方两侧由于较快的溶质渗流呈现出两个橙黄色小尖角;当t=10 a时,系统中部呈现出一个更大的凸起。20 a后的溶质分布在二维系统和三维系统中相对接近,仅在中心区域呈现出明显的差异。另外,图3表明,三维系统中早期的自由对流速度相比于二维系统更快。

图3 不同时间点二维x-z截面和三维x-z中心截面上的溶质羽分布图Fig.3 Solute plume distribution on the 2D x-z cross-section and the 3D x-z central cross-section at different time points
2.2 不稳定性量化分析
根据式(4)计算得到的瑞利数(Ra)为400,远大于Horton-Rogers-Lapwood problem中4π2这一临界值[33-34],预示着自由对流的发生。尽管Horton-Rogers-Lapwood problem中考虑无限延伸的水平多孔介质及常温上、下边界,与Elder problem中的模型和边界设置有所区别,但4π2被众多学者用来评估不同模型中不稳定性产生的临界瑞利数值。然而,瑞利数值与维度无关,无法评判不同维度系统中的不稳定性程度。
图4展示了不同维度系统中自由对流与扩散导致的传质比率(即舍伍德数)随时间的变化。在模拟时间范围内,舍伍德数大于1,表明自由对流引发的质量传递大于扩散过程,系统由于自由对流和扩散处于不稳定状态。然而,除了初始几年的波动,系统总体的不稳定性随着时间推移逐渐下降,由对流占优缓慢过渡至对流、扩散相对平衡的状态。另外,舍伍德数在三维系统中的值大于二维系统,表明三维系统中的对流占优程度更甚于二维系统,三维系统的不稳定性更强。该现象与我们通过观测溶质分布发展的直观感受相违背,即分散指流的产生与否和系统的稳定性程度之间没有直接关联。
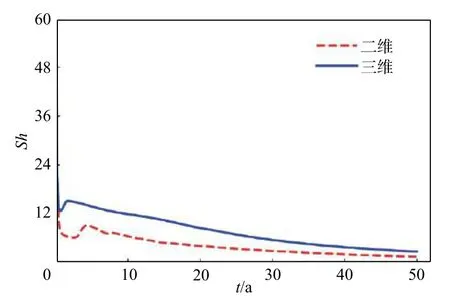
图4 舍伍德数随时间变化图Fig.4 Change of Sh with time
质心位置在z方向上的分布随时间变化情况见图5。二维和三维系统中质心位置随时间的变化趋势一致:前5年,由于强对流入渗,使得质心位置急速下降;质心位置的下降速度随着时间的推移逐渐减慢;10 a后,底部溶质由浓度梯度驱动向上方扩散,导致质心位置缓慢向上迁移。质心在三维系统中的下降速度大于二维系统,这与图3中所观察到的现象一致,可从舍伍德数所传递的信息得到解释,即强不稳定性更易引发快速的对流过程。随着溶质羽向上方区域持续扩散,二维和三维系统中质心的位置趋于一致,并最终向区域中心位置(z=75 m)靠近。
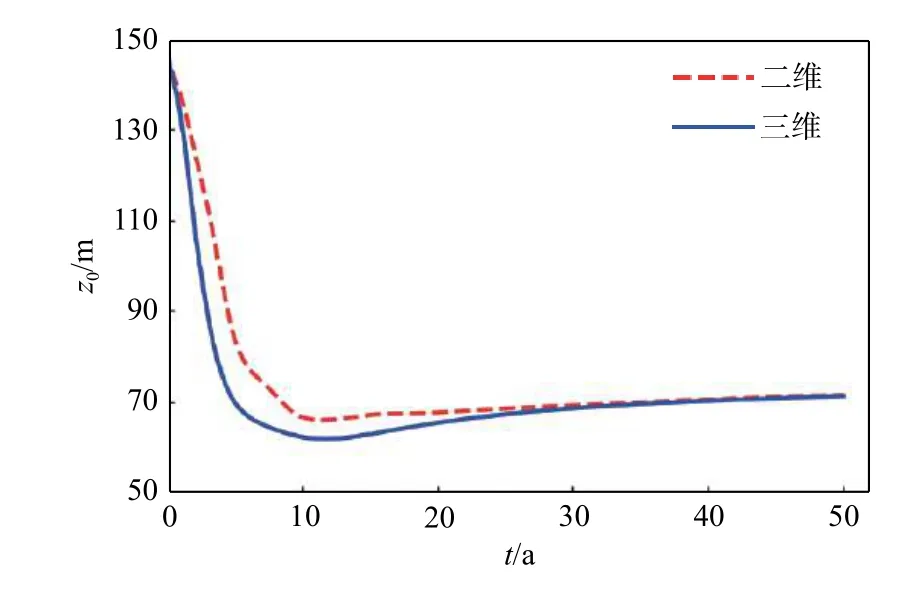
图5 质心位置随时间变化图Fig.5 Change of centroid position with time
2.3 溶质扩散与稀释量化分析
图6展示了溶质在二维和三维系统中相对于质心的扩散程度(m2c向量的模)随时间的变化。由二阶中心矩可以看出,起初,溶质在二维系统中的扩散程度较三维系统更大,随着时间的推移,三维系统中的溶质扩散程度接近二维系统,在 50 a左右达到一致。该现象再次与人们的直观感受相违背。根据常理推测,三维系统额外提供了一个空间方向(y方向)可供溶质扩散,溶质在三维系统中的扩散程度应该比其在二维系统中的扩散程度更大。由此可见,类似于非均质多孔介质条件[32],在涉及自由对流和不稳定性溶质运移时,二阶中心矩同样可能不适用于量化溶质的扩散和稀释。

图6 二阶中心矩随时间变化图Fig.6 Change of the second central moment with time
稀释指数与反应比率随时间的变化见图7。由图7(a)可见,二维系统中溶质的稀释度远小于三维系统,这是由于三维系统中可供溶质扩散的维度增加所造成的。然而,三维系统中的反应比率仅在初始几年略高于二维系统,后续阶段持续低于二维系统,见图7b),说明三维系统中虽然溶质稀释程度大于二维系统,但是可达到的最大稀释度也高,由此二维系统反而更快接近系统最大稀释度。二维和三维系统中溶质稀释增长率分别在 8 a和4 a处出现拐点(斜率急剧变小),可能是由于溶质触底后的稀释速率减小引起的。由于三维系统中溶质羽是成团触底,与模拟区域底部的接触面积较二维系统更大(图3),因此,稀释增长率的减小尤为显著,拐点也更加明显。

图7 稀释指数(E)与反应比率( M )随时间变化图Fig.7 Changes of the dilution index and reaction ratio with time
3 结论
(1)本文通过数值模拟计算了二维和三维系统中的变密度溶质运移过程。结果显示,二维系统中产生了分散指流,而三维系统由于扩散作用的增强抑制了分散指流的产生;然而,三维系统的对流入渗相较二维系统更加迅速,不稳定性更强。由此可见,不稳定性程度与分散指流的产生与否并无直接关联。
(2)稀释指数的计算表明,三维系统中的溶质稀释程度比二维系统更强,然而溶质在二维系统中将更快接近稀释的最大值。传统二阶中心矩可能会错误估计不稳定溶质运移过程中溶质真正的扩散和稀释程度。
(3)本研究限于均质多孔介质等简化条件设置,未考虑非均质、两区动力学传质等复杂情形,在后续研究中应进行进一步深化与拓展。

