双排桩双梁组合支护刚度计算的改进与位移分析

宫凤梧 ，刘 晨 ，郭文娟 ，李晨光 ，封占英 ，张银铂

（河北省地矿局第三地质大队，河北 张家口 075000）

近年来，双排桩作为一种有效抵抗结构侧向位移的新型悬臂类空间组合式支护结构，以其施工便利、桩体受力抗变形效果较好等优势，在边坡支护上得到广泛应用。双排桩支护结构由前排桩、后排桩和连系梁（板）组成，其支护结构受力变形机理设计计算相较于单排桩更为复杂，对此国内外相关学者开展了一系列研究工作。张玲等[1]基于欧拉伯努利双层地基梁理论，利用桩桩、桩土相互作用得到双排桩支护结构在非均质地基中的挠曲微分方程。黄朝煊等[2]基于ABQUES有限元软件对主动与被动土压力地基预加固后双排桩结构内力与位移的影响进行总结和敏感分析，得出预加固的控制效果。高阳等[3]通过三维动态分析对土体力学参数和双排桩设计参数对基坑变形影响进行规律性分析，为双排支护桩设计参数选取提供参考。曹净等[4]依托现行行业规范《建筑基坑支护技术规程》( JGJ 120—2012)提出了3种双排桩桩间土改进等效刚度计算模型，并利用等效桁架模型得出基于等效桁架模型的双排桩结构计算模型。李四维等[5]在紧邻地铁的深基坑双排桩支护工程中利用“时空效应”减少支护变形量，并得出支护过程的桩体变形规律。王祥秋等[6]通过深基坑双排桩室内模型试验，对桩间土加固、桩侧被动区加固、桩端土体加固以及未加固等四种工况下双排桩的力学性能进行分析研究，得出四种工况以桩间土加固效果为最好的结论。张玲等[7]通过弹性地基梁变形方程建立双排桩挠曲变形控制微分方程，根据桩顶桩底边界条件得到一种考虑桩桩以及桩土相互作用的支护结构解析计算方法。曹岩[8]通过平行布设有连梁双排抗滑桩模型试验得到该类型双排桩的弯矩分布规律和桩身的破坏模式。周珩等[9]通过分析双排桩结构挡土墙高度与踵板宽度之比、软土厚度对结构稳定性的影响，得出水平向桩基变形为主要结构变形，应力集中存在于桩顶、桩基锚固点处、底板连接处。易喆[10]探讨了双排桩桩排数、排距、桩长、桩刚度等支护结构参数对基坑边坡变形以及地表沉降的影响。刘青松等[11]研究了双排桩冠梁水平侧向刚度对支护体系变形的影响，并提出了考虑连梁作用的双排桩冠梁水平侧向刚度的建议计算方法。郑轩等[12]通过正交试验法探究双排桩的变形规律，表明前后排桩和冠梁与连梁的变形规律与承载作用。陈香月等[13]使用拉杆连接结构应用双排钢板桩，得到在水平荷载作用下的变形规律。朱庆科等[14]通过分析冠梁平面外假设无限刚与实际有限刚的计算结果可以得出冠梁的刚度参数变化对桩身弯矩的影响幅度和对位移的影响幅度比较接近，以及基坑的长、短边长度、开挖深度、冠梁刚度、土层黏聚力和内摩擦角、支护结构排距和桩距等主要设计参数与空间效应冠梁影响长度的关系。WANG[15]利用有限元软件PLAXIS 3D模拟双排桩不同桩长、桩间距和冠梁长度等参数下的侧向变形和弯矩的变化，提出了用于双排桩作为支护结构设计合理的参数值和考虑土压力的一些建议。杨小明[16]使用ABAQUS模拟不同冠梁与连梁参数下深基坑双排桩前后排桩桩体最大位移、桩身弯矩和刚度的变化。张飞[17]对依托文克勒假设的考虑冠梁与连梁作用的双排桩支护结构计算方法进行简化，且计算得到的解析解比ANSYS数值解偏小。

在国内外目前的深基坑结构设计计算方法中，已对连梁与冠梁作用可以提高排桩支护体系的刚度、调整支护体系的受力并减少桩身位移达成了共识，但连梁与冠梁对矩形双排桩支护作用的结构计算方法还不全面。现有的双排桩支护结构计算模型对连梁和冠梁的作用缺少合理的体现，双排桩支护体系中冠梁的参数多参考经验设置。因此，本文以现有冠梁刚度系数计算方法为基础，优化改进考虑连梁和冠梁作用的基坑矩形双排桩支护结构计算方法，并对双梁组合支护体系下不同土性对双排桩前后排桩桩身最大横向位移的影响进行探讨，以期为双排桩支护结构的理论研究和设计计算提供参考。

1 矩形双排桩冠梁与连梁组合支护体系改进计算模型

双排桩支护体系包括前排桩、后排桩、冠梁及连梁，由组合体系带来整体刚度的提升与空间效应的发挥，并协同桩土工作，达到控制基坑边坡变形、保持坑侧稳定以满足施工现场及周边的安全要求[18]。通过双排桩在工程应用中的经验可知，冠梁和连梁的组合作用对双排桩支护起到有效的作用，依据材料力学与结构力学理论，双排桩冠梁与连梁的组合作用对桩后土压力、桩顶横向位移和深层横向位移等参数有重要影响。以冠梁为研究对象，冠梁在体系内受到横向作用力、力偶和扭矩（扭矩较小可省略）。由此假定冠梁只产生位移而无转动，简化图示如图1所示。

图1 冠梁受力简化图Fig.1 Simplified diagram of the crown beam force

吴刚等[19]分析了冠梁对双排桩的约束作用，并将冠梁的作用分为协调与联系前后排桩的刚性梁以及为空间变形协调作用而在桩刚架结构顶端横向支撑的弹簧，其刚度系数为：

式中：qi、——第i根前、后排桩对冠梁的横向作用力；

di——第i对桩桩顶处冠梁的位移量。

冠梁简化计算示意图如图2所示。在此基础上，分析冠梁对矩形双排桩的空间变形协调作用，为冠梁所受的横向作用力，由冠梁之间纵向正应力以及空间协调的作用力组成，即qi=σ+pi，忽略冠梁纵向位移，第i对桩桩顶处冠梁位移由力学叠加原理可得：

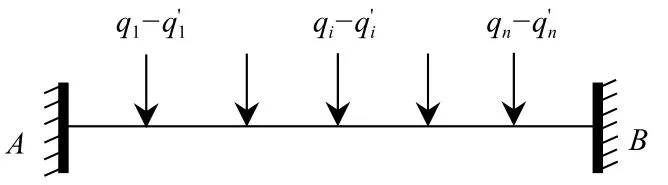
图2 冠梁简化计算示意图Fig.2 Schematic diagram of the simplified calculation of crown beam

式中：δij——单位力作用在j点处时冠梁在i点处的变形。

且此处桩顶处冠梁的弯矩为：

式中：l——冠梁的计算长度；

EI——冠梁的抗弯模量；

aj、bj——单位力作用点j与固定两端A、B的长度；

x——作用点i与A端点的长度。

考虑的空间作用下钢架结构的矩形双排桩在i点的桩顶横向位移dpi和不考虑空间作用情况下的位移d0pi关系为：

式中：δpi——单位水平力作用下桩顶端横向位移。

因为矩形双排桩结构顶端与冠梁横向位移相等，即：

由式（6）计算得到横向作用力合力结合式（2）得到冠梁位移di，进而得到矩形双排桩结构顶端横向支撑刚度系数Ks。

上述计算仅考虑冠梁对双排支护桩的横向约束作用，而由工程应用中的经验可知，双排桩桩顶位移受冠梁与连梁的组合体系的影响较大，因此，将冠梁与连梁的刚性连接作为一个整体，通过组合体系中的惯性矩来计算考虑到连梁作用的矩形双排桩冠梁横向支撑刚度系数。

由于冠梁对支护桩位移的影响与支护桩位置有关，因此工程实际中冠梁与连梁对支护桩位移存在一定效率，引入冠梁与连梁作用效应系数[20]，矩形双排桩双梁组合体系的惯性矩以支护体系中连梁横向中心线为轴线，如图3所示，则双梁组合惯性矩公式为：

图3 矩形双排桩冠梁与连梁组合体系示意图Fig.3 Schematic diagram of the combination system of rectangular double-row pile crown beam and connecting beam

式中：b、b′——冠梁、连梁的高度；

h、h′——冠梁、连梁的宽度；

ξ——冠梁与连梁作用效应系数；

s、n——矩形双排桩桩间距、排距；

ui、uei——第i根桩在有双梁、无双梁约束下桩顶产生的位移。

对改进前、改进后的式（7）进行分析，以冠梁尺寸b×h=0.78 m×0.48 m，连梁尺寸b’×h’= 0.78 m×0.78 m，前后排桩间距s=1.38 m，桩排距n=1.58 m，E=2.6×104MPa，则在不同冠梁计算长度l和考虑冠梁与连梁作用效应系数ξ下矩形双排桩冠梁横向支撑刚度系数计算结果如图4、图5所示。

图4 改进前不同计算长度下的横向支撑刚度系数计算结果Fig.4 Calculation results of the stiffness coefficient of the lateral support under different calculated lengths before the improvement

图5 改进后不同计算长度和冠梁与连梁作用效应系数下的横向支撑刚度系数计算结果Fig.5 Improved calculation results of the stiffness coefficient of the lateral support under different calculated lengths and the effect coefficient of the crown beam and the coupling beam

由计算结果可知，利用考虑了连梁作用后的组合惯性矩计算得到的横向支撑刚度系数明显提高，改进前后刚度系数随冠梁计算长度的增长而逐渐减小，且长度影响逐渐减小，最终几乎可忽略不计；改进后冠梁横向支撑刚度系数随冠梁作用效应系数的增大而逐渐增大，增幅也较大，改进后模型考虑了冠梁与连梁组合体系对支护桩体系位移的影响，其计算结果更为合理，提高双排桩的经济效率。

2 工程实例

2.1 工程概况

工程项目建设场地位于河北省张家口市万全区某医院东侧，根据岩土工程勘察资料，场地埋深35.1 m范围内主要划分为杂填土层（Q4ml）、湿陷性粉土层（Q4l）、圆砾及细砂层（Q4al+pl）和粉质黏土层（Q4l）。拟建建筑物由地上4～9层的住院楼和地下3层的车库组成，场地基础埋深为15 m，自然标高为735.12 m，桩顶标高为0.000 m，基础和结构类型为框架结构和筏板基础，场地内最大荷载为200 kPa，场地勘察深度内未发现地下水，故在本场地建设施工过程中可不考虑地下水对其基础的影响。基坑支护区简图及监测点布点示意图如图6所示，监测点间距为15 m，局部略有调整。场地四周皆为已建小区高层商住楼，且南、北侧与东侧楼距基坑场地较近。

图6 基坑支护区简图及监测点布点示意图Fig.6 Schematic diagram showing the foundation pit supporting area and monitoring points

2.2 支护方案

为不影响周边建筑物设施的结构安全以及基坑正常使用，项目基坑四侧采用双排桩支护方式进行支护，其中西侧（支护一区）前排桩52根，后排桩52根，南侧（支护二区）前排75根，后排77根，东侧（支护三区）前排60根，后排60根，北侧（支护四区）前排81根，后排81根。以南侧（支护二区）为例，双排桩结构设计计算参数见表1，场地土层信息见表2。另外，前排桩钢筋笼纵筋为21E28，箍筋为D16@150，后排桩钢筋笼纵筋为25E28，箍筋为D16@150；连梁纵筋为8E28，箍筋为D22@150。基坑顶部无放坡，基坑周边10 m范围内施工荷载按20 kPa计算。

表1 双排桩结构设计及计算参数Table 1 Design and calculation parameters of the double-row pile structure

表2 土层信息表Table 2 Information of the soil layer

为确保基坑开挖过程中支护结构与周边的安全稳定，对基坑四周均布监测点，监测内容主要为桩顶横向和竖直位移量以及深层桩横向位移量，共布置29个点，其中南侧（支护二区）布置7个监测点。

2.3 结果对比

2.3.1 现场监测结果

现场监测结果如图7所示，监测时间为103 d。由监测结果可知，南侧（支护二区）双排桩桩顶最大横向位移为6.9 mm，深层桩横向位移最大为8.1 mm，监测结果满足规范要求，即双排桩支护体系设计方案满足基坑横向位移要求。

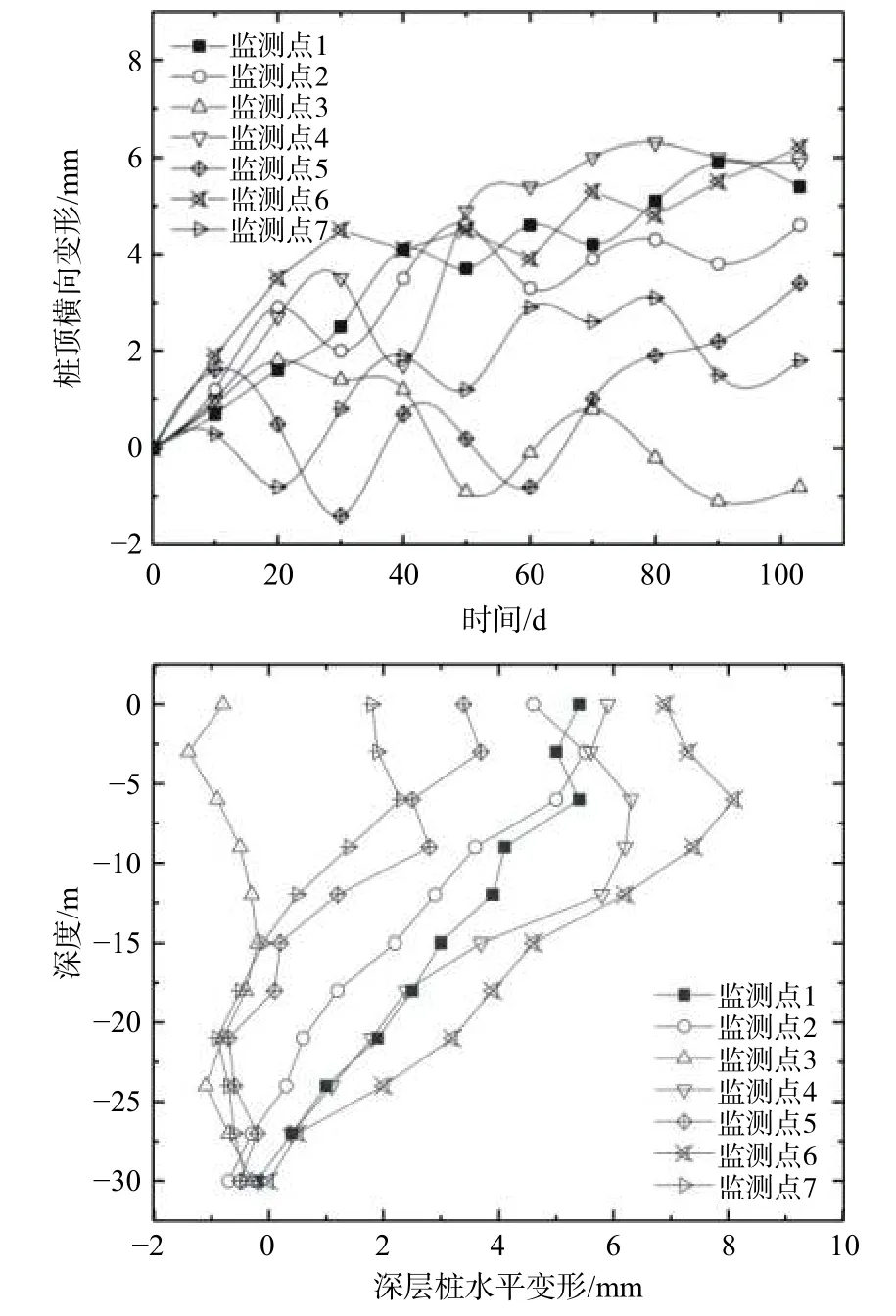
图7 支护二区双排桩桩顶和深层桩最大横向位移Fig.7 Maximum horizontal displacement of the top and the deep part of double-row piles in the supporting area No.2

2.3.2 基于改进计算方法的计算结果

基于工程概况中的矩形双排桩结构计算参数，采用前文改进的考虑双梁组合支护体系理论模型进行计算，得到南侧桩桩顶最大横向位移为8.1 mm，深层桩最大横向位移为8.8 mm。同时，得到不同双梁组合刚度系数下双排桩桩顶横向位移计算值，如表3所示。由表3中可得，双梁组合支护体系组合刚度对桩顶位移有较大影响，组合刚度为40～50 MN/m下的位移与观测值较为贴近。

表3 不同双梁组合刚度系数下双排桩桩顶横向位移Table 3 Horizontal displacement of pile tops of double-row piles under different double-beam combination stiffness coefficients

2.3.3 基于深基坑计算软件的支护结构计算结果

由于理正单元计算采用双排桩独立冠梁刚度计算模型，较实际监测情况和改进后计算模型不同，则基于深基坑计算软件“理正深基坑”，由双排桩支护设计参数得到基坑南侧支护结构设计结果，其中桩顶最大横向位移为11 mm，深层桩最大横向位移为13.8 mm，如图8所示。

图8 基于软件“理正深基坑”得到的支护结构计算结果Fig.8 Calculation results of the supporting structure based on the Lizheng deep foundation pit

由现场监测、基于改进方法计算和基于“理正深基坑”计算软件进行的支护结构计算等3种结果比较可得，改进后的理论计算值较“理正深基坑”软件计算结果更贴近监测值，说明改进的理论模型较为合理，更贴近实际情况，改进后的组合支护体系刚度为40～50 MN/m。

3 双梁组合支护体系下不同土性对双排桩前后排桩桩身最大横向位移的影响

由于冠梁与连梁组合支护体系对双排桩的横向支护约束力是由双排桩前后排桩横向和竖向位移差所造成的，根据横向支撑刚度系数定义，即双梁支护体系横向支撑刚度系数的影响因素之一主要为双排桩横向和竖向位移差。所以，在桩支护范围深度内土层强度的变化将很大程度影响桩的沉降与横向位移量。本文对于不同土层强度的设计参数主要考虑了内摩擦角、黏聚力、土的抗拉强度以及土体水平抗力比例系数m的影响。在相同的土压力作用下，通过设置不同地基土层设计参数，对比基坑开挖至基底后双排支护桩最大横向位移的变化。

由于土层具有分层的特点，在改变参数时，将部分参数变化设置为倍数变化，利用“理正深基坑”计算软件进行结构设计计算。参数设置及计算结果如表4、图9、图10所示。

图9 前、后排深层桩不同内摩擦角下的横向位移Fig.9 Horizontal deformation of front and rear deep piles at different friction angles

图10 前、后排深层桩不同黏聚力下的横向位移Fig.10 Horizontal deformation of front and rear deep piles with different cohesions

表4 双梁组合支护体系下不同土性对排桩最大横向位移计算结果Table 4 Calculation results of force and deformation of row piles with different soil properties under the double beam composite support system

可见双梁组合支护体系下不同土性对双排桩受力变形的整体变化趋势为，随着土层内摩擦角、黏聚力和土体水平抗力比例系数取值的不断增大，前后排桩最大横向位移不断减少，而抗拉强度所引起的位移则几乎不变；在土层内摩擦角和黏聚力取值较小时，前后排桩最大横向位移的变化较大；取值较大时，最大横向位移的变化趋于平稳。由前后排深层桩横向位移规律可得，在基坑埋深以下及桩底范围内桩身存在位移拐点，拐点处各不同内摩擦角、不同黏聚力条件下位移相等。

4 结论

（1）将双排桩冠梁与连梁的刚性连接作为一个整体，引入冠梁与连梁效应系数以改进计算得到的考虑到连梁作用的矩形双排桩冠梁横向支撑刚度系数更高，更符合工程实际。

（2）双梁组合支护体系组合刚度对桩顶位移有较大影响，组合刚度为40～50 MN/m下的位移与观测值较为贴近；冠梁计算长度与引入的冠梁与连梁作用效应系数对双梁组合支护体系组合刚度影响较大，计算长度对组合刚度呈负相关，效应系数对组合刚度呈正相关。

（3）双梁组合支护体系下双排桩前后最大横向位移受土层内摩擦角、黏聚力和土体水平抗力比例系数影响，取值越大，前后排桩最大横向位移越小；土层内摩擦角和黏聚力取值较小时，前后排桩最大横向位移的变化较大，取值较大时，最大横向位移的变化趋于平稳；改变抗拉强度不会影响双排桩桩体位移。由前后排深层桩横向位移规律可得，在基坑埋深以下及桩底范围内桩身存在位移拐点，拐点处各不同内摩擦角、不同黏聚力条件下位移相等。