机器人加工装备运动学镜像模型建立方法与实验研究
南晓萱 王 俊 肖 明 席文明
(厦门大学航空航天学院,福建 厦门 361102)
在自动化制造阶段,操作者通过示教器操纵机器人,形成操作者与机器人的直接关联,这种模式适合大批量、产品单一的制造过程。在数字化制造阶段,为适应多品种、少数量的订单式生产,构建了与物理系统对应的数字系统,即物理系统的镜像模型,实现数字系统对物理系统功能的部分替代,适应快速变化的制造过程[1-2]。在智能制造阶段,为替代物理系统的更多功能,在镜像模型的基础上,实现数据的双向传输,从而建立物理系统与数字系统的数字孪生[3-5],通过物理系统的传感数据,实现对物理系统的模拟、仿真与参数优化[6]。
建立物理系统的镜像模型是实现智能制造的基础,然而,由于机器人制造、安装误差的存在以及机器人串联式结构,其物理机器人几何参数与数字空间中的理论参数并不一致,导致机器人绝对定位精度低。构建物理机器人镜像模型的方法是对机器人的本体和装备进行标定[7],利用标定的参数,实现数字空间中物理机器人的镜像模型构建。标定精度决定着建立的镜像模型精度,从而决定着机器人的作业精度。
现有标定方法没有考虑零位误差,即机器人零位时实际关节角与理论关节角差值对几何参数标定的影响,导致标定后几何参数的较大误差[8],降低了镜像模型精度和机器人的作业精度。本文采用轴旋转法标定方法,实现几何参数与零位的解耦标定。利用坐标变换法建立标定后机器人的运动学方程,借助牛顿迭代法求取运动学逆解。
1 轴旋转法标定机器人关节轴线
图1是标定机器人几何参数的实验系统,由安川MH250机器人(日本安川公司,抓取重量250 kg,工作空间2 700 mm)、Radian激光跟踪仪(美国自动精密工程公司,测量精度为5 μm)以及安装在机器人末端电主轴连接块上的靶球组成。标定过程为:①驱动机器人至零位。②在尽可能大的角度范围内,按一定的角度间隔只旋转一个轴而其他轴固定,记录对应角度间隔的靶球空间坐标。③将靶球安装到电主轴连接块的另一个位置,重复②,即同一个轴测量两次。④标定完一个轴后,重复①~③过程,直到所有关节轴标定完成。

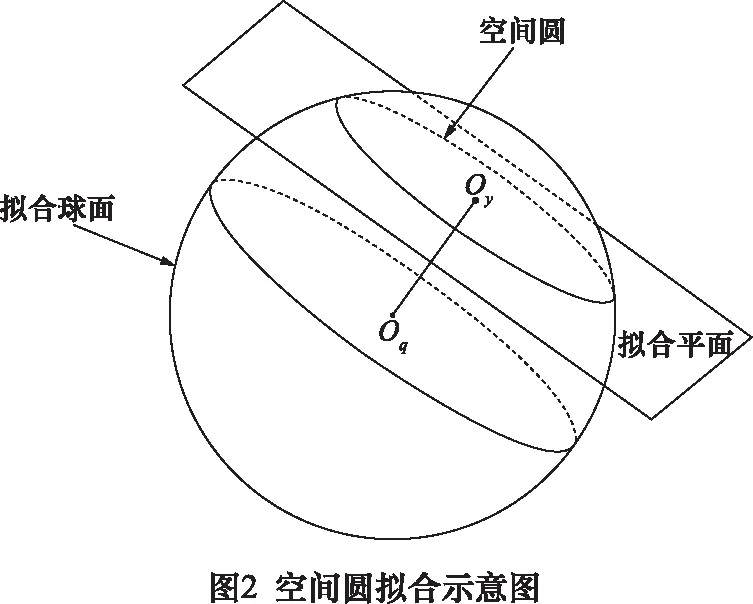
对于记录的同一个轴的两组数据,它们处于绕该轴旋转形成的空间圆上,如果能够利用2组数据求得空间圆的圆心,则2个圆心的连线就是该轴的轴线。计算方法如下:
设测量点的坐标为Ki(xi,yi,zi),i=1,2,...,n。空间平面的方程为:
apx+bpy+cpz-1=0
(1)
将n个测量点代入式(1)中,得:
ApXp-Lp=0
(2)
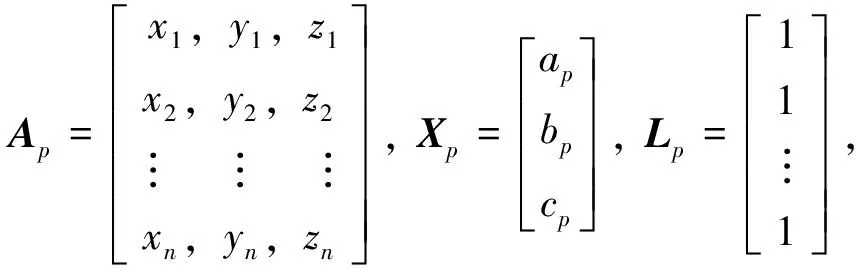
(3)
空间球方程为:
x2+y2+z2-Ax-By-Cz+D=0
(4)
将n个测量点代入公式(4)并以矩阵形式表示:
QqXq-Lq=0
(5)
则其最小二乘解为:
(6)

apx0+bpy0+cpz0-1=0
(7)
又向量O0平行于拟合平面的法向量(ap,bp,cp),则:
(8)
联立式(7)、(8),可得拟合平面与拟合球相交的截圆圆心坐标:
(9)
设第二次拟合圆的圆心为o′(x01,y01,z01),连接两圆圆心,得到轴线的向量为:
n=(x01-x0,y01-y0,z01-z0)
(10)
轴线向量n已知,又轴线过拟合圆圆心o(x0,y0,z0),则轴线方程为:
(11)
2 机器人运动学方程建立
由于制造和安装误差,导致物理机器人的轴线由理论的平行或垂直状态变为不平行、不垂直,并且末端三轴不交于一点,无法采用D-H法建立运动学方程。图2中,{in}表示理论模型的第i轴连杆坐标系,{ia}表示物理机器人第i轴连杆坐标系,li表示机器人基坐标系中第i轴的方向向量。

{in}绕ki轴旋转λi角使旋转后坐标系各坐标轴平行于{ia}坐标系各坐标轴,得到新坐标系{i1n};然后将新坐标系{i1n}沿向量npi进行平移与坐标系{ia}重合,其中:
(12)
由各轴轴线的空间位姿,可以得到物理机器人的零位,见表1所示。
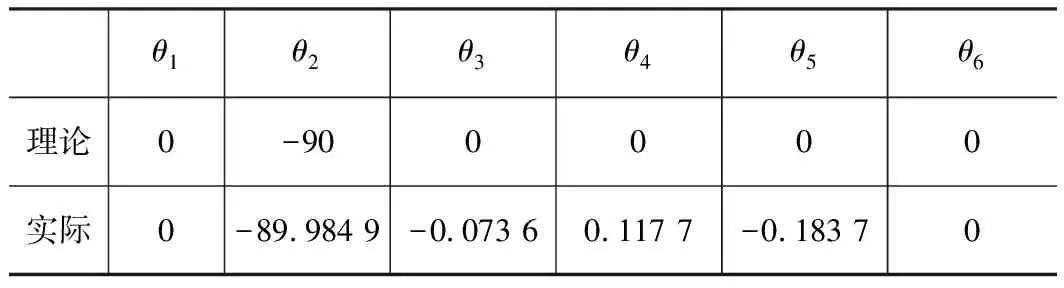
表1 机器人理论零位和实际零位值 (°)

假设理论模型各连杆坐标系相对于机器人基坐标系的位姿矩阵为Ii,则物理机器人各连杆坐标系相对于基坐标系的位姿矩阵Qi可通过式(13)进行求解:
Qi=IiTrans(npix,npiy,npiz)Rot(ki,λi)
(13)
式中:npix、npiy、npix是向量npi在坐标系{in}的3个坐标轴上的投影。
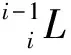


(3)绕{(i-1)2a}的z轴旋转θi,使得{(i-1)2a}的姿态与{ia}完全一致,得{(i-1)3a}。
(4)沿向量Si(Six,Siy,Siz)平移,使得{(i-1)3a}最终与{ia}完全重合。
可得:
(14)
αi=arccos[(a(i-1)xaix+a(i-1)yaiy+a(i-1)zaiz)cosβi-1+
(n(i-1)xaix+n(i-1)yaiy+n(i-1)zaiz)sinβi-1]
(15)
(16)
求得的Qi数值代入式(14)~(16),即可求得物理机器人的连杆参数,见表2所示。
表2 物理机器人连杆参数
物理机器人相邻变换矩阵为:
(17)
其中:s表示sin,c表示cos。
根据正运动学方程的定义,得:
LS=MA
(18)
其中:L为投影矩阵,MA为给定机器人的末端位姿。矩阵取等式两边矩阵的前3行元素对应相等,构造方程组如下:
(19)
其中:f1(θ)~f12(θ)均是关于变量θ(θ1θ2θ3θ4θ5θ6)的多元函数,记为F=[f1(θ),f2(θ),…,f11(θ),f12(θ)]T。物理机器人逆运动学求解的本质是求方程组F关于变量θ的解,使用牛顿迭代法求解该方程组,具体步骤如下:
(1)首先求解方程组F的雅可比矩阵J(θ),并构造θ求解的迭代公式。方程f1(θ)~f12(θ)分别对变量θ(θ1θ2θ3θ4θ5θ6)求偏导数,得到方程组F的雅可比矩阵J(θ),如式(21)所示。
(20)
计算雅可比矩阵J(θ)的广义逆矩阵,并由此得到θ求解的迭代公式,如式(21)所示。
θk+1=θk-[JT(θk)J(θk)]-1JT(θk)F(θk)
(21)
(2)利用机器人理论模型的逆运动学解,作为牛顿迭代的初值θ0。
(3)根据迭代公式(21)更新变量θ的值。
(4)根据加工要求给定迭代精度ξ,本文取小数点后4位。计算关节变化量dθ=θk+1-θk,判断‖dθ‖∞≤ξ是否成立,若成立,取θ当前值作为物理机器人的逆解;若不成立,重复步骤③~步骤④,直至‖dθ‖∞≤ξ成立或超出迭代次数。
3 机器人加工装备镜像模型建立
物理机器人运动学标定完成后,就可以利用标定的参数建立物理机器人的镜像模型。图5a是物理机器人系统,图5b是利用ADAMS软件建立的与图5a对应的镜像模型,其方法是按照标定的参数建立各杆件CAD模型并将其导入到软件中,按照标定的几何参数装配成镜像模型。

建立物理机器人的镜像模型后,还需要建立机器人加工装备的镜像模型,即图5a中的其他单元相对于机器人的位姿,与图5b中的对应单元模型相对于机器人模型的位姿一致。以加工对象为例,设图5a中加工对象的坐标系为{XOYOZO},机器人坐标系为{XBYBZB},它们之间的转换矩阵为J1。图5b中加工对象模型的坐标系为{xoyozo},机器人模型坐标系为{xbybzb},它们之间的转换矩阵为J2。建立机器人加工装备镜像模型的方法为:在物理空间,利用标定后的机器人作为测量工具测量J1的值,然后在镜像模型空间中,利用测量的J1值调整加工对象模型的位姿,即调整{xoyozo}的位姿,使得J2=J1。机器人加工装备中其他单元的镜像模型建立与此相同。
完成物理机器人本体和装备的镜像模型建立后,可以在数字空间中集成刀轨迹生成与后处理模块以及加工仿真模块,实现物理机器人加工前的轨迹生成与优化、加工仿真等。
在图5b中,针对加工对象模型,CAM软件生成的刀轨迹是相对于{xoyozo}坐标系,需要将刀轨迹通过{xoyozo}坐标系,转换到机器人坐标系{xbybzb}中,生成机器人轨迹,这一过程被称为刀轨迹后处理。{xoyozo}与{xbybzb}之间的转换矩阵为J2,通过J2易于将刀轨迹转换成机器人轨迹。
4 实验验证
图6是沿长方体四周加工凹槽,通过测量凹槽加工后的错位误差以及尺寸精度,验证物理机器人与装备镜像模型建立的有效性。采用理论运动学模型控制机器人加工的最大误差为4.02 mm,而采用标定几何参数的运动学模型控制机器人加工的最大误差减少到0.28 mm。通过机器人几何参数的标定,可以有效提高镜像模型的精度,从而提高机器人的加工精度。

图7a是采用变姿态对半球体进行加工,加工时,其刀具轴线指向球心,图7b是完成加工后的半球,图7c是半球加工后的误差测量方法,即沿不同的d处,测量球冠半径R。其中球体半径为50 mm,d值以5 mm为间隔,共测量8次,每次重复测量10次,取其平均值。半球体加工的误差范围为-0.83~+0.52 mm,这其中部分误差来源于电主轴连接块的安装和制造误差,导致镜像模型空间与物理空间的工具中心点(TCP)坐标系不一致而形成的误差。
5 结语
本文利用轴旋转法标定方法求取物理机器人的几何参数,利用求取的几何参数构建物理机器人的镜像模型,为物理机器人数字孪生体的构建建立了基础。后期,将利用机器人厂家提供的开发库,获取物理机器人的状态参数以及加工参数,实现物理系统与数字系统间的数据双向传输,建立物理机器人系统的数字孪生体,实现加工过程的监督与加工参数的优化。


