异形结构内甲烷赋存态模拟

林 轩，白永强，张 雁，吕秀丽，宋胜浩，姜继玉，张翠婷

(1.东北石油大学 物理与电子工程学院，黑龙江 大庆 163318； 2.东北石油大学 地球科学学院，黑龙江 大庆 163318；3.吉林大学 超硬材料国家重点实验室，吉林 长春 130012)

随着常规油气资源可采储量的日益减少，非常规油气资源已经成为如今能源产业发展的重要对象[1-2]。页岩气作为典型的非常规油气资源已成为世界能源的研究热点之一[3-4]。游离态、吸附态是页岩气在富有机质页岩中的主要存在形式[5-6]，页岩中吸附气含量一般占总含气量的20%～85%[7]。页岩气的主要成分是甲烷，甲烷在页岩孔隙中的吸附量与页岩的有机质含量、类型，储层温度、压力，孔隙的类型大小等都有关系[8-11]。因此，甲烷在页岩孔隙中的赋存机制是复杂的分子动力学行为。

吸附是分子以能量最低的状态聚集到物质表面的一个过程。吸附作用通常分为2种：物理吸附、化学吸附[12]。尤其是有机质对于天然气的吸附是一种物理吸附[13-14]。范德华力为分子间的主要作用力[15]。

蒙特卡洛方法(Monte Carlo Simulation，MC)与分子动力学方法(Molecular Dynamics，MD)是研究页岩储层中的甲烷吸附特性的有效方法[16-19]。巨正则系综蒙特卡洛法(Grand Canonical Monte Carlo，GCMC)是体系保持恒温、恒压的状态下进行的蒙特卡洛模拟，GCMC方法在对吸附行为的模拟中占据了重要地位[20]。许多学者建立三维碳纳米管来代替页岩中的有机质孔隙，模拟甲烷在三维碳纳米管中的各种行为。张廷山等[21]建立了三维碳纳米管探讨了甲烷和二氧化碳在页岩储层有机质孔隙中的微观分布特征、相对密度、自扩散系数，确定了页岩气最优埋深，获得了二氧化碳置换技术开采页岩气的最佳埋深范围。HONG等[22]对各种尺寸的开放式单壁碳纳米管进行了气体吸附研究，采用GCMC方法模拟了甲烷在其中的吸附，讨论了温度和单壁碳纳米管直径对气体吸附容量的影响。LIU等[23]建立了三维碳纳米管，对甲烷和二氧化碳进行了不同组分的混合气体模拟，获得了不同组分的混合气体在特定条件下的吸附、解吸的异同。不同于三维碳纳米管，部分学者建立石墨狭缝代替有机质孔隙。张宇[24]基于GCMC，研究了选择不同孔径分布范围的狭缝孔隙，对甲烷的吸附特征进行了模拟，结合实验表征了孔径分布对甲烷吸附能力的影响。AMBROSE等[25]对甲烷在石墨狭缝中进行了模拟，获得了甲烷在石墨狭缝中的密度分布，通过研究密度分布，发现了甲烷的分层现象。陈磊等[26]采用分子动力学模拟的方法研究了温度、压力以及狭缝表面的水滴对甲烷吸附情况的影响。陈国辉等[27]利用分子模拟方法模拟了甲烷在有机质孔隙中的吸附作用，根据密度场分布及分子结构图等阐明了页岩气在孔隙表面的赋存状态。实际上，三维碳纳米管与石墨狭缝都与实际的页岩有机质孔隙有着很多差异。

虽然目前学者对页岩孔隙已经有很多研究，但甲烷在页岩孔隙内吸附的模拟主要局限于使用石墨狭缝或者三维碳纳米管来代替页岩有机质孔隙，但实际页岩孔隙中存在着许多不规则孔洞[28]，它们并非平整光滑，所以真实的页岩孔隙不能以理想的狭缝或者理想的圆孔完全代替。这些不同形状、不同大小的孔洞，会影响甲烷的吸附量与甲烷在孔隙中的赋存状态。而页岩中这种孔隙大规模存在，会导致相同模拟状态下与规则孔隙获得模拟结果很不相同。

基于上述分析，笔者通过对比实际页岩的扫描电子显微镜(Scanning Electron Microscope，SEM)照片，利用Materials Studio (MS)软件构建微观的三维异形孔隙模型，使用更符合实际的椭圆孔隙代替规则的圆形孔隙，并在椭圆孔隙的基础上构建2种类型的三维异形孔隙，运用蒙特卡洛方法与分子动力学方法研究甲烷在三维异形孔隙中的赋存状态，并对其微观机理进行分析，以期为页岩气的气藏储量评估提供借鉴。

1 吸附模拟

1.1 模拟软件的选择

模拟借助Accelrys公司的MS软件进行，MS软件为使用者提供了一个优异的模拟环境，可以帮助研究者构建并分析分子的结构模型，为表面与固体结构模型优化与分析提供了较为完善的环境，可以研究并预测构建模型所具有的相关性质[29-30]。模型使用MS软件中的Visualizer模块构建，Visualizer模块可以实现不同分子模型的构建，更加直观的表现分子的构象、构型，还可以通过其携带的不同优化模块来进行模型的空间最优化[31]。

1.2 模型构建

纳米级有机质孔隙在页岩中广泛存在，而有机质与甲烷有很好的亲和力，因此这些有机质孔隙是甲烷赋存的重要场所。有机质的主要成分为干酪根，干酪根的组成根据演化历史的不同、沉积的不同而变化，因此并没有固定的化学构成，干酪根以碳基为骨架，故本模拟的模型以碳基为基础进行构建。

图1为四川盆地志留系龙马溪组渝参4井662.1 m页岩岩心典型SEM照片，图1(a)为页岩扫描电镜照片，其中灰色为页岩无机基质，黑色为干酪根有机基质及孔隙，图1(b)为图1(a)有机质区域放大，图1(c)为图1(b)的2次电子像，其中圆形、三角形和矩形标示区域为不同特征孔隙区域。通过对比发现，图1(c)中圆形、三角形与矩形所标示的孔隙与规则圆形孔隙有较多差异。

图1 四川盆地志留系龙马溪组渝参4井页岩孔隙特征

为了模拟与实际页岩孔隙相符合的页岩孔隙，分别构建了图2所示的4种孔隙。图2中每幅图左为正视，右为斜侧视。黄色菱形标记处为曲率半径特征点。图2(a)为规则圆形孔，使用碳纳米管进行代替，碳纳米管作为外边界，对内部的气体进行约束，所以使用armchair型碳纳米管即可。本研究构建(20，20)单壁armchair型碳纳米管进行模拟研究，直径为2.576 nm，管长4.919 nm。根据图1(c)中圆形所标示孔隙，设计了如图2(b)所示的规则椭圆孔进行模拟，椭圆的长轴为2.828 nm，短轴为2.303 nm，管长为4.919 nm。图1(c)中的三角形所标示的孔隙，都有一个共同的特性，就是从整体来看，孔的形状是在椭圆的基础上有某处向椭圆外部突出的特征，突出的两侧平稳的变回椭圆的轮廓，根据这一特性，在椭圆上进行改动获得了如图2(c)所示的“突出”形状的孔隙，孔隙管长4.919 nm。图1(c)中矩形所标示的孔隙都有一个共通的特性，整体孔的形状在椭圆的基础上在某处都会向椭圆内部凹陷，根据这一特性，在椭圆上进行改动获得了如图2(d)所示的“凹陷”形状的孔隙，孔隙管长4.919 nm。在所有模型构建完成后对模型进行几何优化，使用Fortice模块中的最速下降法进行优化，最终获得较为符合实际的孔隙。图2中菱形所标注位置为曲率半径特征点(曲率半径Rt)。改变曲率半径可获得不同“突出”和“凹陷”形状的孔隙结构。全文模型视图以图2中正视图为准，自左向右为x轴正方向，自下而上为y轴正方向，垂直于x，y轴向里为z轴正方向。

图2 4种与电镜照片相切合的碳原子基孔隙

图3为构建的甲烷分子，构建流体甲烷分子后使用Fortice模块smart进行优化，优化后的甲烷分子键长为0.109 nm，键角为109.7°。

建立晶格参数为a=3 nm，b=3 nm，c=4.919 nm，α=β=γ=90°的盒子进行模拟。x，y，z方向均为周期性结构。由于本次研究孔隙边界在实际中都被岩石所固定，因此在模型优化结束后将整个模型视为刚性结构。

1.3 模拟理论

本模拟中的力场选择最适合有机质的COMPASS力场[32-33]。在COMPASS力场中甲烷分子与碳基模型之间的相互作用势、甲烷分子与甲烷分子间的相互作用势均采用Lennard-Jones(L-J)势能模型[34]。对于所有模型的L-J势能参数和电荷参见表1[35]。通过使用L-J势函数，可以对整个系统的共价键分子之间的范德华力进行准确描述，其中ε为势能阱深(εi或εj为第i或第j个粒子的势能阱深)，σ为粒子的尺寸作用参数(σi或σj表示第i或第j个粒子的尺寸作用参数)，rij为粒子i，j间距离，q为粒子的带电量(qi或qj为第i或第j个粒子的带电量)，kB为玻尔兹曼常数，则L-J势函数U(ij)可表示为

表1 L-J势能参数

(1)

εij，σij使用Lorentz-Berthelot(L-B)混合规则求出：

(2)

(3)

模拟方法使用的蒙特卡洛方法，蒙特卡洛方法是指在一个不断重复的时间序列中，获取大量的样品进行统计，以此来对近似解进行统计。本文所使用是巨

正则蒙特卡洛方法(GCMC)。在GCMC方法下进行的模拟，模拟的粒子发射源与所建立的盒子进行粒子交换，因此在盒子中，粒子的运动可以大致分为3种，即粒子位置的改变、盒子中粒子的增加、盒子中粒子的减少。

在巨正则系综中要以逸度代替压力来进行计算[36]，针对本文的研究对象，选用P-R状态方程来进行压力与逸度的转换，R为摩尔气体常数，R≈8.314 J/(mol·K)，T为系统的温度，Vm为气体的临界摩尔体积，则系统的压力p可表示为

(4)

(5)

其中，Tc为气体的临界温度；pc为气体的临界压力。

式(4)中的a通过式(6)求出：

(6)

式(4)中的α(T)为

α(T)=[1+k(1-Tr0.5)]2

(7)

其中，k与Tr可以通过式(8)，(9)求出。

k=0.374 64+1.542 26ω-0.269 92ω2

(8)

(9)

式中，ω为偏心因子。

对于纯组分的气体逸度系数φ的求法为

(10)

式中，Z为气体的临界压缩因子；A与B通过如下公式求得：

(11)

(12)

其中,a，b，α(T)已通过式(5)～(7)求出。

通过上述公式求出逸度系数，再通过式(13)完成压力与逸度的转换。

甲烷的临界常数与偏心因子见表2[37]。

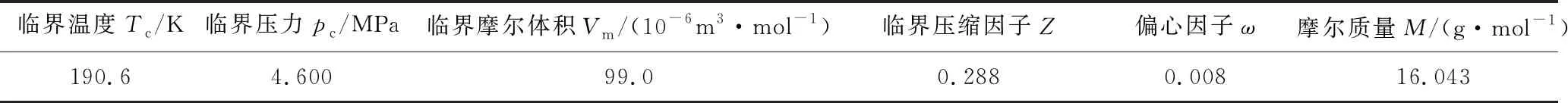
表2 甲烷的压力逸度转换参数

f=φp

(13)

以上所有模型的吸附均采用MS软件中的Sorption模块进行，模拟温度为340 K，压力为30 MPa，模拟过程中吸附骨架全程保持固定且无初速度，模拟总步数1×107，平衡步数5×106。得到吸附构型后，对获得的模型进行动态模拟，使用Andersen[38]热浴控制温度，范德华力与静电作用力分别采用Atom-based方法与Ewald方法，截断半径为1.5 nm。模拟时间步长1 fs，模拟总时间500 ps。

2 结果与讨论

2.1 圆形孔与椭圆孔中的密度分布

2.1.1圆形孔与椭圆孔中的甲烷排布方式

图4为圆形孔隙与椭圆孔隙的甲烷密度分布瞬时图，其中图4左图红点表示甲烷出现的概率密度，图4右图中白色球表示氢原子，灰色球表示碳原子。比较椭圆孔隙与圆形孔隙中甲烷的排布方式，发现在整体上2种孔隙中的甲烷吸附状态存在共性：一是甲烷沿着2种孔隙内壁进行排列分布，产生了2层吸附，分别称为第1吸附层与第2吸附层；二是即使甲烷严格沿着内壁进行吸附，甲烷的排列依旧不是十分规整(图4右图)，通过测量发现，每个甲烷与壁面的距离并不是完全一致，这可以推断即使甲烷在吸附层中也是处于运动状态的，并不是稳定静止的。虽然对于同一模型，每次模拟获得的甲烷瞬时构型图并不完全相同，但是甲烷出现的概率密度分布是相同的。另外，吸附态的甲烷运动状态可能受孔径大小、储层压力等因素影响[39-40]。

图4 圆形孔隙与椭圆孔隙的甲烷密度分布瞬时示意

对2种孔隙中的甲烷赋存状态进行细节观察，发现在部分位置上吸附行为存在着不同。在模型自下而上0.75 nm处(图4左图绿线位置)，椭圆孔隙与圆形孔隙的甲烷吸附密度存在差异(图4左图)，这说明甲烷在孔隙中的赋存状态与孔隙形状密切相关。

2.1.2圆形孔与椭圆孔中的甲烷密度分布

由于椭圆与圆在y轴方向上具有对称性，所以以模拟孔隙距离的一半为准，对下半部分进行研究。在图5所标示2处位置分别进行统计，统计层厚度为0.1 nm，统计层1为图4左图中的绿线所示位置，统计层2在竖直y轴方向的正中部。为了获得甲烷密度分布曲线，需进行密度转换，在水平x轴方向上，将统计层分成多份，每份占据的距离约为0.1 nm。设甲烷分子量为M(CH4)，统计层内甲烷分子数为N，每份统计层的面积S，统计层厚度h，并最后将单位转化为g/cm3，则吸附气的甲烷密度ρ表示为

(14)

如图6所示，由于建立的模型为对称模型，孔隙内甲烷密度分布曲线对称性很好，而且因为建立的模型都为单层碳壁模型，所以排除了多层壁面原子作用势叠加的影响，不同形状孔隙内甲烷的分布更为清晰。

统计层1在横向-0.3～0.3 nm处，椭圆模型内甲烷密度较为稀疏，密度在0.15～0.20 g/cm3，规则圆形模型内甲烷较为密集，密度在0.23～0.27 g/cm3。密度分布曲线在±0.5 nm处形成了第1吸附层。圆形孔隙第1吸附层形成的峰跨度要大于椭圆孔隙第1吸附层形成的峰的跨度，这是椭圆与圆的几何性质决定的。2者第1吸附层的峰值有所区别，椭圆孔隙的第1吸附层的峰值为0.849 g/cm3,略大于圆形孔隙的第1吸附层的峰值0.737 g/cm3。由此可见，由于椭圆孔隙与圆形孔隙的结构不同，在孔隙中相同区域的吸附情况也不同。

统计层2所显示的甲烷密度分布曲线，与前人的研究结果整体趋势基本一致[41]。曲线显示2者都形成了2层吸附，而孔隙内中间区域的游离气密度相近，均在0.320 g/cm3左右。但是代表第1吸附层和第2吸附层的主峰密度有较大差异。圆形孔隙中甲烷第1吸附层峰值为0.620 g/cm3，第2吸附层峰值为0.408 g/cm3，2个峰值之间空隙中甲烷的密度为0.245 g/cm3，低于游离气密度；椭圆孔隙中甲烷第1吸附层峰值为0.565 g/cm3，低于圆形孔隙中甲烷吸附层密度，第2吸附层峰值为0.482 g/cm3，而2个峰值之间空隙中甲烷的密度为0.303 g/cm3，比圆形孔隙中的高，接近于游离气密度。整体而言，对比圆形孔隙和椭圆孔隙中甲烷密度分布情况发现，形状的改变对吸附特征及细节有较多改变。

2.2 “突出”孔隙中的甲烷密度分布

2.2.1“突出”孔隙的甲烷排布方式

通过改变图2(c)中标注位置的曲率半径，获得3种不同的“突出”孔隙，曲率半径分别为0.460 nm(图7(a))，0.240 nm(图7(c))，0.147 nm(图7(e))。图7(a)，(c)，(e)所代表的孔隙形状在下文分别称为P1，P2，P3。模拟结果显示，甲烷沿着3种孔隙内壁进行排列分布，与常规孔隙相同[22]都形成了明显的2层吸附，然而靠近孔隙内壁的第1吸附层特征有着明显差异。

随着曲率半径的减小，孔隙内的甲烷密度逐渐减小。孔隙中的突出部分都有甲烷聚集，在聚集部分的后侧都有明显的空缺。当曲率半径为0.460 nm时(图7(a))，沿内壁的甲烷吸附层尚能沿着内壁进行吸附，当曲率半径达到0.240 nm时(图7(c))，吸附层呈现断裂。在突出部分后的凹陷处，甲烷的吸附状态从正常的沿着内壁轮廓吸附逐渐变为了在的凹陷顶点两侧聚集，在图7(e)中这一现象尤为明显。

2.2.2“突出”孔隙的甲烷密度分布

在图8中取4个位置分别为甲烷最下部的聚集处、甲烷最下部的聚集处之后的空缺、空缺后的甲烷聚集、上半部分的椭圆第2吸附层处，取统计层厚度0.1 nm，使用式(14)对4个统计层的甲烷进行密度计算，做统计层1，2，3，4的密度分布曲线。

在统计层1中(图9(a))，发现在突出位置有明显的甲烷聚集。但由于突出部分大小的限制，突出部分只能容纳一个完整的甲烷，其他甲烷虽有进入此处的趋势，但由于分子间的作用力，导致被排除在外。P1，P2，P3中甲烷在统计层1中的密度分别为0.684，0.617，0.578 g/cm3，呈下降趋势，由于P1模型特征点曲率半径较大，也使得突出部分曲率较小，说明甲烷有有向平缓空间聚集趋势，式(1)也能解释这一特征，距离太近相互作用势较大，使得甲烷不能在此空间更多存在。

在统计层2中(图9(b))。所选的位置甲烷在统计层1处聚集后的空缺。根据甲烷密度分布图，P1在统计层2处的第1吸附层处可以拥有一个完整的甲烷分子，所以P1还未形成断层。P2，P3中2者的密度有差异，但由于2者都不能拥有一个完整的甲烷分子，所以都形成了断层。在统计层2处，P1，P2，P3所对应的甲烷分子密度分别为0.417，0.071，0.053 g/cm3，P1处密度大于游离气密度，P2，P3处密度很小。断层出现的位置都在突出部分与孔隙内部衔接界面处，可以判断出狭小的空间中，甲烷分子受到侧壁碳原子作用势能更大，导致在该位置无法存在甲烷分子。

这一趋势在统计层3中(图9(c))有较明显的缓解。由于更加靠近孔隙内部，该位置的甲烷密度P1，P2，P3分别为0.732，0.277，0.241 g/cm3，密度都有所增长。

在统计层4中(图9(d))。虽然3种孔隙的上半部分都是椭圆的原型，但是在±(0.6～0.7) nm位置3种孔隙第1吸附层的甲烷密度依旧呈现P1>P2>P3，对应的甲烷密度分别为0.801，0.732，0.661 g/cm3。这说明下半部分的孔隙形状变化对整体孔隙的甲烷吸附状态也存在较大影响。这点在第2吸附层上也明显体现。对应第2吸附层依然是P1(0.581 g/cm3)> P2(0.520 g/cm3)>P3(0.303 g/cm3)。

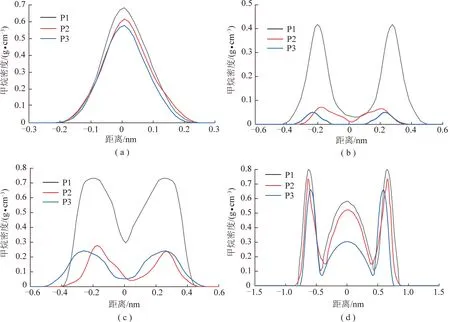
图9 “突出”孔隙中的甲烷密度分布曲线

将统计层1，2，3，4结合对比发现，孔隙形状对甲烷吸附影响明显。在曲率半径的影响下，孔隙内的平均甲烷密度变化较大。随着曲率半径的减小，孔隙内平均甲烷密度逐渐减小，孔隙中心处的游离气逐渐减少直至游离气几乎消失。随着曲率半径的减小，甲烷沿内壁的第1吸附层从连续变为逐渐出现断层，这些都与分子势能随空间变化相关。

2.3 “凹陷”孔隙中的甲烷密度分布

2.3.1“凹陷”孔隙的甲烷排布方式

通过改变图2(d)中标注位置的曲率半径，获得3种不同的“凹陷”孔隙。曲率半径分别为0.315 nm(图10(a))，0.261 nm(图10(c))，0.180 nm(图10(e))。图10(a)，(c)，(e)所代表的孔隙结构在下文分别称为Q1，Q2，Q3。模拟结果显示，甲烷沿着2种孔隙内壁进行排列分布，也形成了明显的2层吸附，然而甲烷的第2吸附层特征有着明显差异。

随着曲率半径的减小，孔隙内的甲烷密度逐渐减小。随着内陷程度逐步加深，突出部分甲烷聚集后开始出现空缺(图10(a))，随后沿内壁形成的第1吸附层也开始出现断裂(图10(c))，内陷程度继续加深，断裂保持但不如“突出”孔隙中的断裂明显(图7(c)，7(e)，10(c)，10(e))。

图10 不同“凹陷”孔隙的甲烷密度分布瞬时示意

随着内陷程度逐步加深，内陷处的第2吸附层上移(图10(c))。当曲率半径为0.18 nm时(图10(e))，内陷处的第2吸附层与上半部分的第2吸附层重合。由于在图10(e)中甲烷的上下部分的第2吸附层完全重合，虽然甲烷的平均密度会随着曲率半径的减小而减小，但是在这个位置可能会导致甲烷密度略大。

2.3.2“凹陷”孔隙的甲烷密度分布

在如图11的模拟图中取3个位置分别为甲烷最下部的聚集处、甲烷最下部的聚集处之后的空缺处、上半部分的椭圆第2吸附层处，取统计层厚度0.1 nm，使用式(14)对3个统计层的甲烷进行密度计算，做统计层1、统计层2、统计层3的密度分布曲线。

在统计层1中(图12(a))。两侧的突出部分有明显的甲烷聚集。Q1，Q2，Q3中的甲烷密度随着曲率半径的减小呈下降趋势，分别为0.547，0.499，0.421 g/cm3，这与“突出”孔隙中的甲烷分布规律一致。

在统计层2中(图12(b))。所选的位置甲烷在统计层1处聚集后的空缺。在±0.8 nm的位置上，Q1，Q2的密度分别为0.325，0.177 g/cm3，Q3的密度为0.479 g/cm3，大于Q1，Q2的密度，这是因为当曲率半径为0.18 nm时(图10(e))，”凹陷”程度的影响，断层位置尚未到达界面处，依然处于一个狭小的空间中，甲烷分子同时受到两侧壁碳原子作用势能，导致空缺位置被压缩，甲烷密度值增高。±0.5 nm处Q1，Q2，Q3的密度分别为0.498，0.361，0 g/cm3。Q1，Q2在该位置更加靠近孔隙内部，空间变大，甲烷受到壁面的作用减小，密度随之增加。

在统计层3(图12(c))中。在±0.6 nm处的密度Q1(0.582 g/cm3)>Q2(0.556 g/cm3)>Q3(0.471 g/cm3)，说明“凹陷”孔隙中，下半部分的形状改变对整体孔隙中的甲烷吸附也有影响。从±0.4 nm开始出现的第2吸附层中Q1，Q2依然遵循这个规律，但是Q3有些不同，由于Q3中上下部分的第2吸附层重合，导致甲烷密度的增加，Q3在第2吸附层上的密度高达0.494 g/cm3，比相对平均密度较大的Q1密度为0.451 g/cm3，Q2的密度为0.302 g/cm3更大，而且Q3中的游离气基本消失。

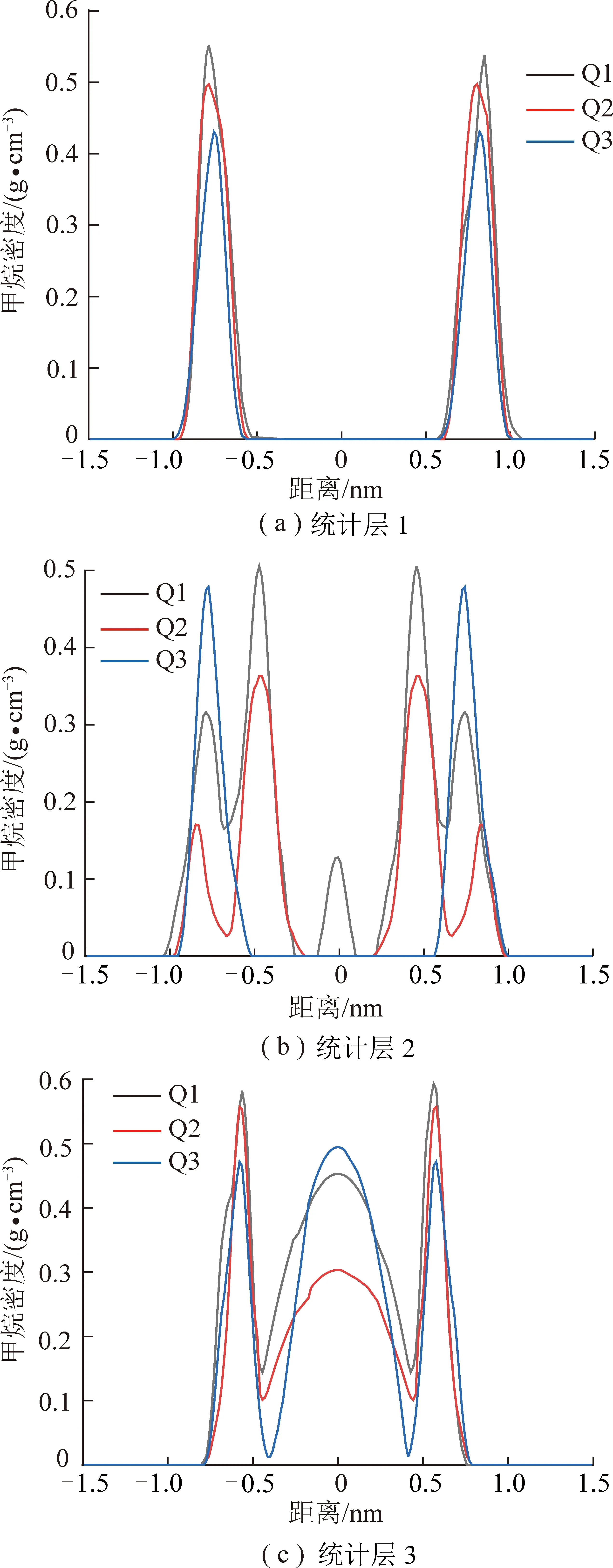
图12 “凹陷”孔隙中的甲烷的密度分布曲线

2.4 “突出”孔隙与“凹陷”孔隙中甲烷密度的分布规律

“突出”孔隙与“凹陷”孔隙中的突出部分都有甲烷的聚集，且密度较为接近，这是由于内部空间较小，聚集概率密度大，但是分子间距离较短，分子间静电力较大，导致甲烷很难再进入突出部分内[42]。

对比图7，10的甲烷密度分布，“突出”孔隙的甲烷的概率密度要比“凹陷”孔隙的甲烷的概率密度大。经过计算，P1，P2，P3的平均甲烷密度分别为0.163，0.148，0.134 g/cm3，Q1，Q2，Q3的平均甲烷密度分别为0.151，0.140，0.111 g/cm3，“突出”孔隙的平均密度大于“凹陷”孔隙的平均密度。

P系列和Q系列孔隙中都存在突出与凹陷位点。但是整体形状的不同，孔隙中甲烷分布的规律也不同，2种形态同时存在同一个孔隙中时，互相影响。在Q系列孔隙中，随着凹陷部分的加深，导致突出部分狭小空间加长(图10(e))，这种“凹陷”孔隙中的突出部分对甲烷的影响相对于“突出”孔隙中的突出部分是不同的，尤其体现在吸附断层形态上(图7(e)和图10(e))

“突出”孔隙与“凹陷”孔隙都会影响游离气的存在，但是方式略微不同。“突出”孔隙随着曲率半径的减小，第2吸附层与游离气密度逐渐减小直至游离气几乎消失，第2吸附层密度十分稀疏但依旧存在。“凹陷”孔隙中随着凹陷程度逐渐增大，最后凹陷部分的吸附与上半部分的第2吸附层完全重合，游离气消失。

实际的地质体系中，孔隙表面的缺陷与官能团对甲烷的吸附也会产生影响，相对于平整的碳基，甲烷分子更优先吸附在缺陷中的碳原子上方[43]。孔隙形状的改变与孔隙表面的变化(缺陷、官能团的改变)两者之间的耦合对甲烷分子的影响有待研究。

3 结 论

(1)以碳基为有机质骨架，圆形孔隙和椭圆形孔隙中甲烷吸附特性比较来看，在第1吸附层上，圆形孔隙的密度(0.620 g/cm3)大于椭圆孔隙(0.565 g/cm3)；而在第2吸附层上，圆形孔隙的密度(0.408 g/cm3)小于椭圆孔隙(0.482 g/cm3)。在2层吸附层之间的空隙上，椭圆孔隙的密度(0.303 g/cm3)比圆形孔隙的密度(0.245 g/cm3)更大，接近游离气密度(0.320 g/cm3)。

(2)“突出”孔隙随着特征曲率半径的减小，孔隙内平均甲烷密度逐渐减小，孔隙中心处的游离气逐渐减少直至游离气几乎消失。并且随着曲率半径的减小，甲烷沿内壁的第1吸附层从连续变为逐渐出现断裂，这些都与分子势能随空间变化相关。

(3)“凹陷”孔隙随着特征曲率半径的减小，孔隙内的甲烷密度也逐渐减小，沿内壁形成的第1吸附层也出现断裂，但不如“突出”孔隙中的断裂程度明显。并且随着曲率半径的减小，内陷处的第2吸附层上移直至内陷处的第2吸附层与上半部分的第2吸附层重合。

(4)“突出”孔隙中的平均密度要略大于“凹陷”孔隙中的平均密度。孔隙下部的形状的改变会影响上部的甲烷赋存状态。