融合深度信息的判别式相关滤波跟踪

高 晨，翟 优，郭希维

（陆军工程大学石家庄校区，河北 石家庄 050000）

0 引 言

视觉目标跟踪系统在智能监控、机器人、无人驾驶、工业自动化等很多领域具有广泛的应用前景。根据目标表观模型的不同，视觉目标跟踪分为基于生成式模型的目标跟踪和基于判别式模型的目标跟踪等两大类。判别式相关滤波（Discriminative Correlation Filter, DCF）跟踪将相关滤波器理论应用于目标跟踪，可在频域进行分类器学习和跟踪，极大地加快了目标跟踪速度，具有很强的鲁棒性，是目前视觉目标跟踪研究的重点方向之一。

文献[1]提出Mosse算法，将相关滤波引入跟踪领域，但该方法的分类器训练样本有限。在此基础上，已有学者将梯度直方图（HOG）、颜色名（CN）、颜色直方图（DAT）、卷积神经网络（CNN）等人为特征作为训练相关滤波器的特征，提高算法准确性。文献[2]通过循环矩阵扩充样本集合，跟踪过程中需要保证目标位置和目标尺度准确性。文献[6]和文献[7]分别提出尺度池和尺度金字塔进行目标尺度估计。此外，在跟踪过程中出现严重遮挡时，目标特征会发生变化，易出现目标丢失现象，需要及时对跟踪结果的优劣进行判断。文献[8]提出平均峰值相关能量（APEC），用以决定是否更新目标特征模板。文献[9]在跟踪中加入检测算法，判定失败时，对目标进行重检测，确定目标正确位置。文献[10]提出ECO算法，有效减少了深度学习特征维数、参数过多的问题。文献[11]提出GSF-DCF算法，利用多通道图像表达进一步提高精度。

综上，基于DCF的视觉目标跟踪算法架构日益完善，同时采用了图像灰度、HOG和深度学习特征等，算法性能逐渐提高，但算法复杂度日益加大，算法运行速度无法满足跟踪系统的实时要求。因此，本文结合实际跟踪系统，做出以下改进：使用跟踪系统搭载的传感器，量测目标深度信息，将更具鲁棒性的距离特征融入DCF框架，设计基于D-DCF框架的跟踪系统。

1 跟踪系统框架

跟踪系统框架如图1所示，流程如下：

图1 跟踪系统框架图

（1）初始化位置滤波器、尺度滤波器、预测目标深度模型，控制云台旋转使光轴对准目标。

（2）由激光测距传感器输出当前目标深度至CA模型，估计当前帧目标空间位置、运动状态，计算得到目标预测深度。

（3）输入新一帧图像，提取图像特征描述目标，利用二维位置滤波器和一维尺度滤波器在候选区域提取低维特征对目标位置和尺度进行估计。

（4）构建目标位置置信度指标，对上一步位置估计结果可靠性进行判别。若满足置信度要求，则更新位置滤波器模板，反之将目标预测位置作为目标新位置，预测位置由第2步估计的目标空间位置计算得到。

（5）结合自适应尺度因子，进行目标尺度估计，提取目标尺度样本，提高尺度精确性。

（6）将估计的目标位置与尺度输入至硬件跟踪系统，控制云台旋转对准目标，获取新一帧图像，重复2～6步，直至跟踪停止。

2 目标跟踪算法改进

2.1 DSST和ECOHC算法原理简介

DSST和ECOHC算法中设计了位置滤波器和尺度滤波器，前者进行当前帧目标定位，后者进行当前帧目标尺度估计。DSST和ECOHC算法将输入信号设计为维特征向量，而后建立损失函数构造最优相关滤波器，则有：

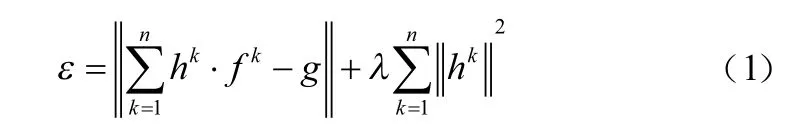
式中：表示特征的某一维度；是正则项系数，目的是消除输入信号频谱中的零频分量；为期望输出。在频域中求得式（1）的解为：

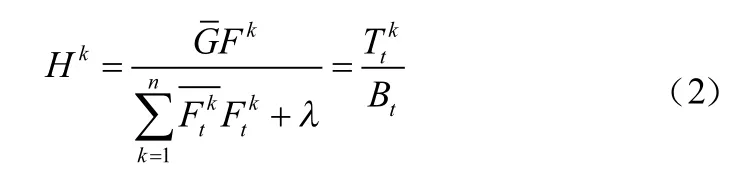
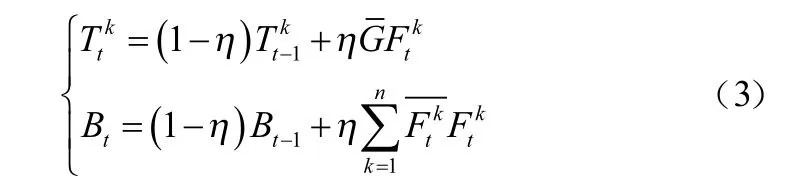
其中为学习率。在新的一帧中目标位置通过求解相关滤波器最大响应值得到，即：

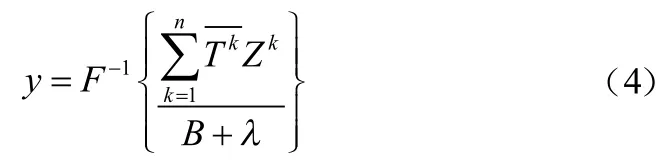
同时，上述方法适用于基于一维独立的相关滤波器的尺度搜索和目标估计方法。用于目标尺度评估的目标样本尺度选择原则为：

式中：、分别为目标在前一帧的宽度和高度；为尺度因子，=1.02；为尺度总级数，=33。

2.2 基于CA模型预测目标深度

本文算法融合目标深度信息，因此需要准确预测目标的深度。因为目标运动的先验知识很少，很难用数学表达式精确表示，只能在各种假设条件下用近似方法予以描述。本文的应用背景为实时跟踪地面目标，量测频率高于目标运动状态变化频率。因此在一个量测周期内，可视目标做匀加速直线运动，其运动状态可用三阶匀加速CA模型描述为：

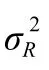
设目标在三维空间内运动，则式（6）中的目标运动状态变量()可以定义为：

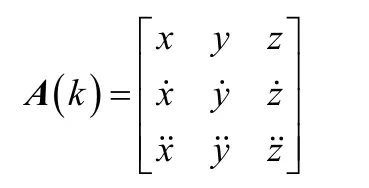
其中、、分别表示目标在三个方向的位置分量。

以目标做“S”形运动为例，如图2所示，以跟踪系统为原点建立三维直角坐标系。首先，系统以为周期量测目标的深度信息和云台姿态角（俯仰角γ、偏航角θ），利用几何关系与运动方程计算目标于时刻的运动状态()，则有：

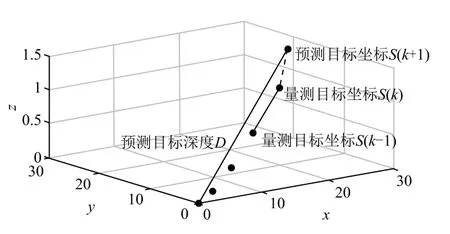
图2 预测深度原理图

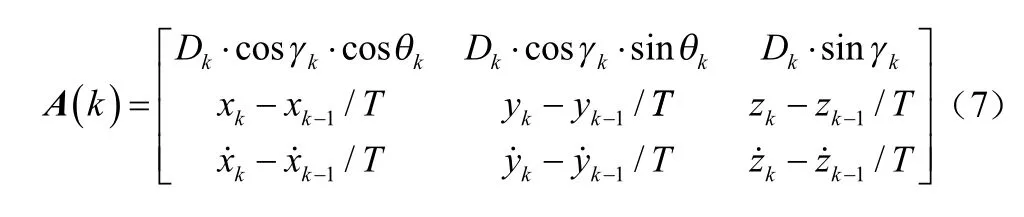
将离散坐标点组合，得到目标路径序列()∈, ...,S。将+1时刻与时刻之间的运动路径近似为直线（如图2中虚线），即下一个量测周期内三维方向目标做匀变速直线运动。将式（7）中的()代入式（6），可以预测下一时刻运动状态(+1)，最终计算得到下一时刻目标的距离为：

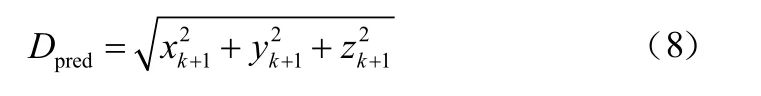
2.3 目标位置置信度判别式

在实验中发现，由于HOG特征和HC特征鲁棒性不强，在背景复杂或目标被遮挡时会出现目标丢失的情况。为了增强特征鲁棒性，提升跟踪精确性，本文融合预测深度构建目标位置置信度判别式。构建原理如图3所示。

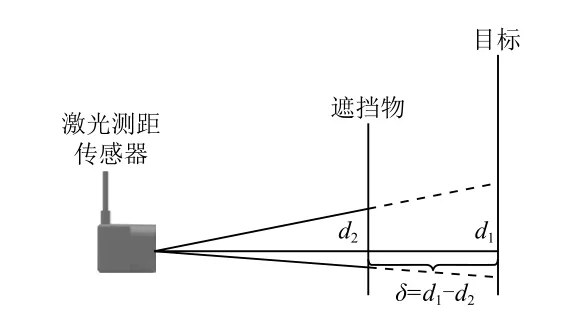
图3 构建目标位置置信度判别式

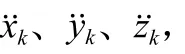
2.4 自适应尺度因子

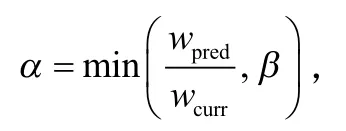
DSST和ECOHC算法是在上一尺度的基础上直接提取33个样本，精确性不高且极大地增加了计算复杂度。为减少尺度样本数量，提高跟踪精确性与实时性，本文对算法做出如下优化：利用预测目标深度计算自适应尺度因子，与时刻目标尺度相乘，得+1时刻预测目标尺度；而在目标中心位置，提取17个尺度样本{......}，对尺度样本进行相关滤波后，找到令滤波器响应最大的尺度，该尺度即为目标尺度。图4为自适应尺度因子的计算过程。

图4 计算自适应尺度因子

记为目标真实宽度，为摄像头焦距，为像元大小，为目标深度，为目标图像宽度，下标last、curr、pred分别表示上一帧、当前帧、预测帧。式（10）、式（11）为根据比例关系计算的目标预测宽度、目标真实宽度。

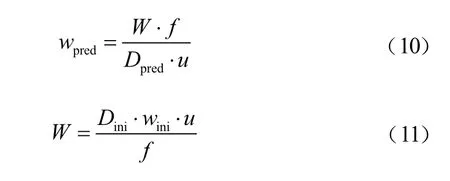
式中：和分别为初始化目标深度和目标图像宽度。将CA模型预测的目标深度与式（11）代入式（10），得到预测目标宽度为：

为了适应目标运动造成的尺度变化、提高尺度准确性以及减少尺度采样数量，本文基于目标深度信息，引入目标宽度自适应尺度因子。对于目标高度自适应尺度因子的计算，与上述过程相似，则有：

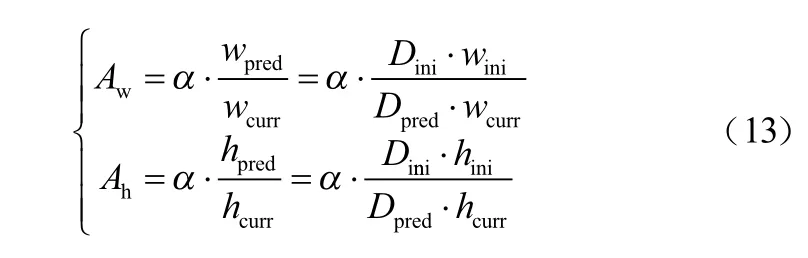
3 跟踪系统硬件设计

设计云台跟踪系统如图5所示。

图5 跟踪系统硬件设计

系统采用STM32F103C8作为主控芯片，云台搭载摄像头、激光测距器，能够完成深度信息采集、图像采集、舵机控制、与上位机通信的任务。二轴云台由两个总线舵机驱动，分别控制偏航和俯仰两个方向的旋转。舵机型号为LX-224，采用单总线通信方式，内部带有控制器完成角度PID、电流PID控制，只需要一条串口指令就可以使其旋转到给定角度，误差不超过±0.24°。激光测距模块能以100 Hz的频率测量深度，分辨率为1 cm，能够满足本文测量目标深度信息的要求。摄像头是USB接口的CMOS摄像头，这种摄像头可通过USB接口直接与计算机相连而无需图像采集卡，易于开发。

4 实验结果与分析

4.1 实验场地与环境

由于本文提出的跟踪算法需要利用目标的深度信息，而现有的公开测评集多是基于2D图像序列，无法提供深度信息；且目标深度信息是激光测距传感器采集所得，需要舵机旋转以确保深度属于跟踪目标。因此，本文设计了两个实验，实验场地情况如图6所示。

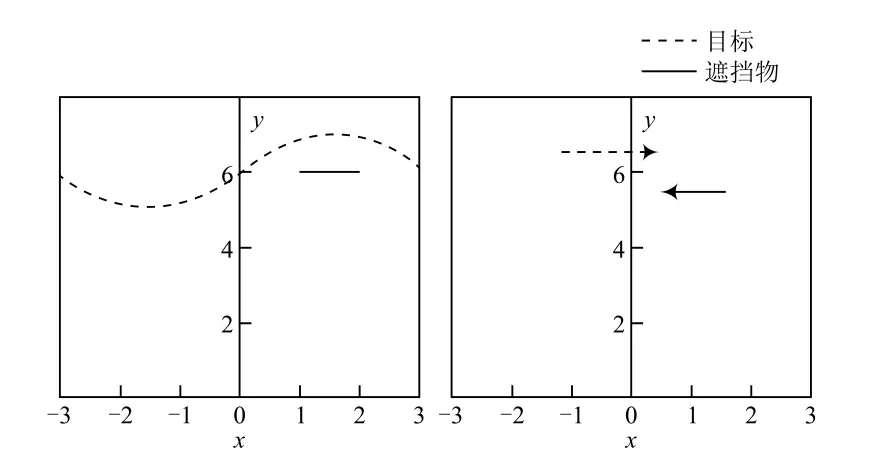
图6 实验场地情况

实验环境：CPU采用Inter（R）Core（TM）i5-7300HQ CPU@2.5 GHz；内存为12 GB；操作系统为Windows10；框架为MATLAB2017a。

4.2 跟踪系统性能与分析

从准确性和实时性两个方面评估跟踪系统性能。准确性：引入跟踪概率P，在工作时间内，当目标中心与图像中心偏差大于固定阈值时，0.2 s内修正偏差跟踪目标则视为成功（计入成功跟踪时间t），否则视为失败。实时性：以算法的每秒处理图像帧数（Frames Per Second, FPS）为评判依据。图7对比了六种算法在实验中的跟踪情况，图片右下角的A～F分别表示D-DSST、DSST、D-ECOHC、ECOHC、ECO、GSF-DCF算法，1～3分别表示跟踪的初始阶段、遮挡阶段、结束阶段。表1为跟踪性能实验结果。由此可以得出：相较于DSST、ECOHC算法，改进后的算法D-DSST和D-ECOHC的跟踪概率更高且未出现目标丢失情况，帧率满足实时性要求；ECO算法使用神经网络提取特征，虽然也能够克服遮挡干扰，但速度慢，难以应用于实际跟踪；GSFDCF算法同样采取神经网络提取的特征，所以跟踪速度慢，目标离开视场，跟踪失败。

图7 六种算法下跟踪系统的实验情况

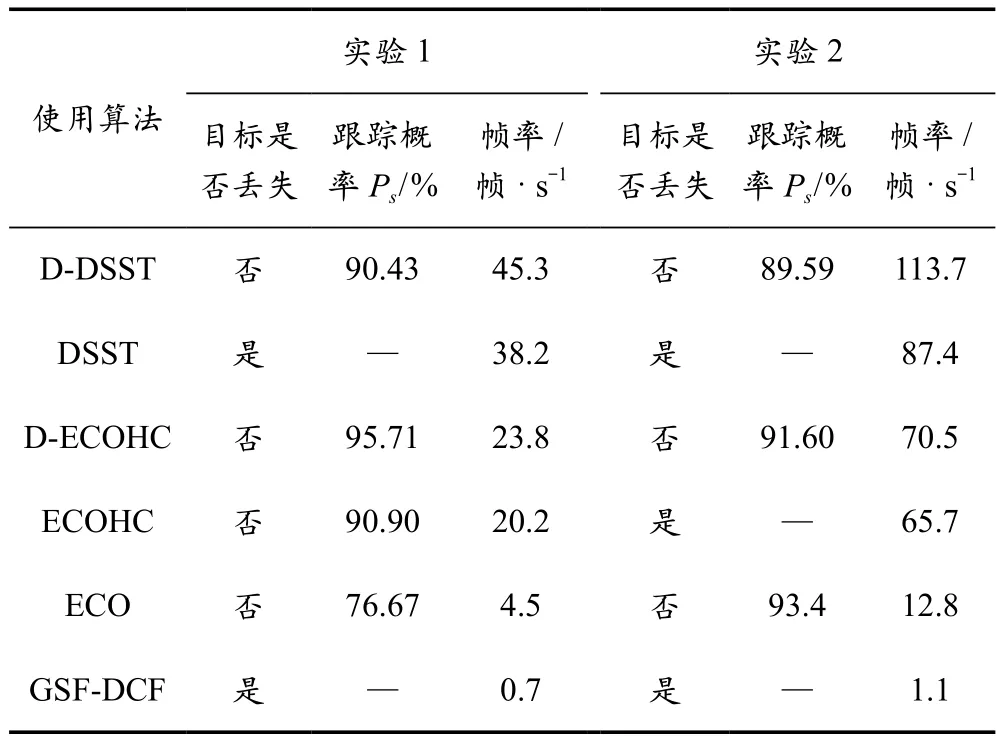
表1 跟踪系统性能实验结果

5 结 语

当前基于判别式相关滤波（DCF）视觉目标跟踪算法的跟踪系统存在尺度估计不精确和容易丢失目标的问题，设计稳定实时的跟踪算法仍是业界研究的难点及重点。本文通过融合激光测距器的深度信息，改进目标跟踪系统的算法。实验结果表明：在有遮挡、背景复杂、目标运动的情形下，基于D-DSST、D-ECOHC的跟踪系统平均跟踪概率分别为90.01%、93.66%，与原算法相比没有出现目标丢失现象；平均帧率分别为79.5 帧/s、47.2 帧/s，较原算法分别提升16.7 帧/s、4.3 帧/s。系统能够克服遮挡干扰，且满足稳定可靠、精度高、实时性良好等要求。