噪声相关非线性系统加权观测融合估计算法*
赵 明, 李 云
(哈尔滨商业大学 计算机与信息工程学院,黑龙江 哈尔滨 150028)
0 引 言
从输入数据中过滤掉噪声和干扰信息,获取实用信息的操作称为滤波,使用的设备称为滤波器。按照滤波器的输出和输入之间如果存在线性关系,则称为非线性滤波器,否则为线性滤波器[1,2]。非线性滤波[3,4]的输入与输出之间存在逻辑运算,如最大值滤波器、最小值滤波器和中值滤波器等。非线性滤波没有固定的模板,也没有特定的传递函数。
现在的非线性滤波算法中,都是假定系统噪声与观测噪声互相独立的。但是实际应用中,由于受表内环境的影响和离散化观测信息,噪声相互独立的条件有时很难得到满足,当系统噪声相关时,现有的非线性滤波算法误差很大,甚至发散。文献[5~7]给出的是带相关噪声的线性系统的估值器。文献[8~12]给出的是带相关噪声的非线性系统的单个传感器估值器,但是没有给出多个传感器系统的融合估计算法。因此,噪声相关情形的非线性滤波问题是具有理论和现实意义的[13,14]。基于贝叶斯估计框架,解决相关噪声估计问题有两个基本的方法。一种是去相关方法[15,16],通过变换将相关噪声变换为不相关的;另一种是Gauss近似递归(Gauss approximation recursion,GAR)滤波器框架[17,18]。
有文献[19]基于Taylor级数逼近方法,提出了加权观测融合(weighted measurement fusion,WMF)非线性滤波器。文献中给出的算法可以统一处理非线性系统融合估计问题,但该算法的缺点是需要在线计算Taylor级数展开项系数,在线计算负担重。Gauss-Hermite(G-H)逼近方法是通过固定点采样、Gauss函数和Hermite多项式逼近任意初等函数,该逼近方法具有很好的拟合效果。
为了解决系统噪声和观测噪声相关的问题,本文基于Gauss-Hermite逼近方法和加权最小二乘法,提出了噪声相关非线性系统WMF容积卡尔曼滤波器(cubature Kalman filter,CKF)。为了降低计算负担,改进了Gauss-Hermite近似方法,采用分段求解方法,离线计算分段的加权系数矩阵。与最优集中式融合算法相比,本文给出的加权观测融合算法精度略低,但是可以显著减少计算量。该算法可以处理非线性多传感器系统融合估计问题。
1 问题阐述
考虑非线性多传感器系统
xk+1=fk(xk)+Γwk
(1)
(2)



(3)
式中 E为均值号,上标T为转置号,δtt=1,δtk=0(t≠k)。
2 带相关噪声系统的去相关
对于式(1)和式(2),考虑了系统噪声与观测噪声相关的情形,本文采用去相关方法,将相关噪声转换为不相关噪声,进而集中融合算法得到了广泛的应用。
定理1对于式(1)和式(2),噪声不相关的集中式观测融合系统(centralized measurement fusion system,CMFS)可以重写为
(4)
(5)
其中
(6)
(7)
(8)
(9)
(10)
(11)
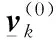
(12)

(13)
噪声独立系统的系统噪声统计特性为
(14)

(15)
证明:由式,合并L个观测方程,得到式(5)和式(9)~式(13)。由系统式(1)和式(2),式(1)可以写为
(16)
由此可以得到式(4)、式(6)和式(8)。新系统的系统噪声和观测噪声是不相关的,即
(17)
3 基于Gauss-Hermite逼近的非线性系统WMF算法
3.1 标量Gauss-Hermite逼近


fp[(x-xi)/γμ]
(18)
3.2 基于Gauss-Hermite逼近的非线性系统WMF算法
对于噪声独立的新系统式(4)和式(5)。但是对于多传感器系统,尤其是针对传感器网络,集中式融合算法由于扩维会带来巨大的计算负担。而且对于噪声相关的非线性系统,在去相关的过程中需要将所有观测方程扩维,这使得计算量明显增加。

(19)
(20)
(21)

(22)


(23)
引理2[19]对于噪声相关系统式(1)和式(2),基于Gauss-Hermite逼近的近似加权观测融合方程为
(24)

(25)
(26)

(27)

4 基于Gauss-Hermite逼近的噪声相关非线性系统WMF-CKF算法
对于非线性Gauss滤波递推公式,需要各种近似策略,将递推公式转换成可实现的滤波公式,本文采用的是基于3阶球面—相径容积规则的CKF算法的实现[22]。系统式(1)和式(2),当系统噪声和观测噪声相关时,本文提出的WMF-CKF算法如下:
1)初始化
2)计算基本容积点和其对应的权值
3)计算状态预测值和误差协方差矩阵
4)观测更新
5)状态更新
转到第2步迭代计算。该算法可处理噪声相关的非线性多传感器系统的融合估计问题。噪声相关的WMF-CKF算法框架如图1所示。

图1 噪声相关的WMF-CKF算法框架
5 仿真实例
考虑一个带有4传感器的非线性系统
xk=fk-1(xk-1)+wk
=0.4xk-1+xk-1/(1+(xk-1)2)+cos(0.1(k-1))+wk
(28)
(29)

(30)
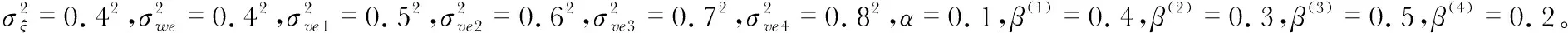
观测方程
(31)
由去相关定理1有
(32)
其中
(33)
(34)
仿真结果如图2,图3所示。从图中可以看到估计效果良好。

图2 WMF-CKF估计曲线

图3 CMF-CKF估计曲线
本例采用累积均方误差(AMSE)[20],作为衡量系统准确性的指标函数如式所示,得到的AMSE曲线如图4所示。

图4 局部CKF、WMF-CKF及CMF-CKF的AMSE曲线
(35)
由图4可以看出,集中式融合CKF估计精度最高,接着是基于Gauss-Hermite逼近的加权观测融合CKF算法,4个局部CKF估计算法(LF1~LF4)估计精度最低。
由图2~图4可以看出,本文提出的去相关加权观测融合CKF滤波算法的有效性。
6 结 论
1)考虑系统噪声和观测噪声相关的非线性系统,利用去除相关的方法,得到噪声独立的新系统;
2)基于Gauss-Hermite逼近方法为了减小计算负担,采用分段的Gauss-Hermite逼近方法分段计算;
3)在结论(1)和结论(2)的基础上,提出了WMF算法,压缩降维,降低计算负担.
4)结合CKF滤波算法,提出了非线性WMF-CKF算法。与CMF-CKF算法相比,WMF-CKF估计精度相当,但大大的减小了计算量。

