电容式MEMS压力传感器的稳健设计研究*

吕 博, 谭晓兰, 刘胜强

(北方工业大学 机械与材料工程学院,北京 100144)

0 引 言

随着电子科技、集成电路技术以及微机电系统(micro-electro-mechanical system,MEMS)器件制造工艺的不断发展,MEMS传感器依靠其诸多优点得到了迅速发展,如,体积小、质量轻、能耗低以及适应恶劣工作环境能力强等。电容式MEMS压力传感器具备良好的重复性和长期稳定性,虽然电容式压力传感器由于其工作原理,导致其输出为非线性的,但是通过传感器的信号处理功能,对传感器线性特性的要求已不必要,而较高的灵敏度则是必需的[1～5]。

由于传感器在制造过程中有很多不可控因素,如制备环境、工艺误差、设备误差等,尤其是对于MEMS器件来说,微小的变差将造成更加显著的影响[6],所以,对整个MEMS压力传感器进行稳健优化设计就显得极为重要。稳健设计是指影响产品性能的可控因素和不可控因素(即噪声因素)在一定范围内产生波动时,仍能保持产品质量特性稳定的一种工程设计方法[7,8]。

基于随机模型,本文对一种电容式MEMS压力传感器进行了稳健设计研究。结果表明:该稳健设计方法不仅可以保证传感器具有较高的灵敏度,还能保证设计解的稳健性,从而提高传感器的可制造性,降低生产成本。

1 电容式压力传感器的理论分析

电容式MEMS压力传感器的结构如图1所示[9]。此传感器主要由三个元件组成：感压膜片、电容器以及机械耦合元件(中心柱)。当外部压强P作用在感压膜片上时,感压膜片发生弯曲变形,且中心处变形最大,通过机械耦合元件,将感压膜片中心处的变形传递给移动板,此处中心柱的尺寸足够小,故可以忽略对感压膜片变形产生的影响。

移动板在中心柱的驱动下向上移动,电容间距变小,电容量发生改变。通过外接电路测得电容变化量ΔC,再经公式推导,便可以求出作用在感压膜片上的压强P,从而实现传感器测量压力的功能。

当外部压强作用在感压膜片上时,感压膜片发生弯曲变形,根据经典的薄板小挠度弯曲理论[10],可得薄板的挠曲线方程为

(1)

式中D=Eδ3/12(1-μ2)。

由于圆形薄板周边为固定边,所以边界条件为

ωρ=a=0,dω/dρ=0

(2)

故可以得到

(3)

圆形薄板中心处变形最大,ρ=0,故

(4)

平行板电容器的电容表达式为

(5)

当移动板由于感压膜片变形而向上移动距离ωmax时,电容变为

(6)

故电容变化量为

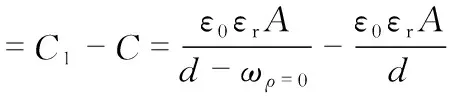
(7)

由此,便可以得到电容式压力传感器的灵敏度表达式为

(8)

2 电容式压力传感器的稳健设计

2.1 设计变量

通过对电容式MEMS压力传感器工作原理的分析[11],得知影响传感器性能的主要参数有：感压膜片半径r1,感压膜片厚度δ,动膜半径r2,平行板间距d以及它们各自的变差,即r1,δ,r2,d,Δr1,Δδ,Δr2,Δd,故设计变量为

X=(r1,δ,r2,d,Δr1,Δδ,Δr2,Δd)T

=(x1,x2,x3,x4,x5,x6,x7,x8)T

(9)

2.2 噪声因素

在实际问题中的随机因素通常分为以下两种基本形式：第一种是在测量或试验某个物理或力学性能时所得到的数据的不确定性；第二种则是由随机过程和偶然因素造成的不确定性。这两种随机性都可以用服从某种特定概率分布的随机变量来表示[12]。

通过对模型的理论分析,可得知影响电容式MEMS压力传感器的噪声因素有：真空介电常数ε0,相对介电常数εr,感应膜片的弹性模量E,感应膜片的泊松比μ,外界压强P以及许用弯曲应力[σ],故噪声因素可表示为

Z=(ε0,εr,E,μ,P,[σ])T

=(z1,z2,z3,z4,z5,z6)T

(10)

2.3 质量特性

质量特性是用来评价一个工业产品质量好坏的性能指标。本文将电容式MEMS压力传感器因受到外部压强而产生的电容变化量ΔC作为MEMS传感器的设计特性,为了提高产品的质量性能,并且使其波动尽可能地小,因此,以电容变化量负值的均值及方差的望小特性作为产品的质量特性[13],并求解最小值,即

(11)

式中w1和w2为加权系数。

(12)

2.4 约束条件

由于感压膜片的材料为多晶硅,具有较大的弯曲刚度,因此感压膜片的挠度将远小于它的厚度,故本文采用小挠度弯曲理论来分析感压膜片的弯曲变形[14],因此

ωmax≤0.2x2

(13)

由于圆形薄板受均布载荷作用,边界固定,故其最大弯矩和最大弯曲应力发生在板边处,其值分别为

(14)

最大弯曲应力应小于许用弯曲应力,即σmax≤[σ]。

综上所述,此稳健设计数学模型的约束函数为

(15)

2.5 随机稳健设计模型

综上,建立随机稳健设计模型

(16)

式中 (Ω,F,P)为概率空间,gj为约束条件,βj为事件发生的概率,此处将βj设为1,即满足约束条件的概率为100 %。

3 随机稳健设计模型求解

3.1 稳健设计算法程序

根据上述所建立的稳健设计数学模型,编写相应的算法程序,将其目标函数和约束条件编写到模块文件的算法程序中,并将设计变量和噪声因素等其他参数编写到数据文件中,运行随机模型算法程序进行求解,其程序模块结构示意图如图2所示。

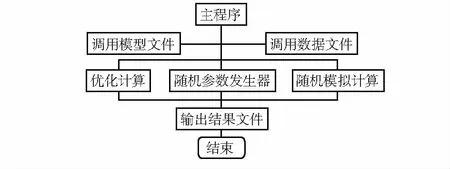
图2 程序模块结构示意

3.2 设计变量及噪声因素

设计变量的初值以及上下界值如表1所示。

表1 设计变量的初值与上、下界值 μm

经查阅文献[15]可知,本文所考虑的噪声因素遵循的概率分布类型和参数如表2所示。

表2 噪声因素所遵循的概率分布类型和参数

3.3 结果分析

运行相应的算法程序,并调试有关参数,便得到了随机模型稳健设计解,将其与原方案进行比较,结果如表3所示。

表3 原方案与随机模型稳健解对比

基于随机模型的稳健设计方案考虑了现有的MEMS加工制造误差,设计合理容差,使得当设计变量产生变差时其设计解依旧可行,保证了传感器的稳健性；同时稳健设计优化后的电容变化量ΔC明显增大,由原方案的27 fF增加到了47 fF,提高了传感器的灵敏度。

4 结 论

1)将稳健设计方法理论应用于MEMS传感器的研究具有一定的可行性。

2)提出的稳健设计方法提高了传感器的灵敏度。根据稳健设计解和式(8)可得到，灵敏度由原方案的2.7 aF/Pa增长到4.7 aF/Pa,提高了大约74 %。

3)由于考虑了传感器尺寸的变差以及噪声因素的影响,使得稳健设计解可以保证产品的质量性能对尺寸参数在生产过程中发生变差不敏感,从而提高了MEMS传感器制造的成品率。

4)将依据稳健设计解制作电容式MEMS压力传感器样品,并对其输出特性进行测试,为其提供了理论依据。