基于GA-BP神经网络的气体传感器湿度补偿研究*

廖有为, 曹伟嘉, 蒋剑锋, 杨留方

(1.云南民族大学 电气信息工程学院,云南 昆明 650031;2.云南省高校无线传感器网络重点实验室,云南 昆明 650031)

0 引 言

气体传感器测量时易受环境湿度的影响[1],不同湿度影响输出精度,因此需要对湿度补偿。湿度补偿一般有硬件补偿和软件补偿两种。硬件补偿存在补偿电路受电子元件漂移和元件焊接的精密度影响、调试困难等缺点,致使整个测量电路的可靠性降低,而且还存在成本较高的问题[2]。软件补偿的方法主要有插值法、最小二乘法、多项式拟合法,但是这些软件补偿方法存在计算量较大、拟合精度低等缺陷[3]。神经网络具有很好的非线性拟合能力,本文提出使用改进反向传播(back propagation,BP)神经网络和利用遗传算法(genetic algorithm,GA)全局搜索优化BP神经网络补偿传感器湿度误差[4]。

1 湿度对传感器的影响

SnO2气敏元件对湿度敏感的根本原因是吸附的H2O分子与SnO2气敏材料发生化学反应所致,当环境相对湿度升高(即空气中水分子浓度增大),加速了分子在气敏材料表面的吸附,自由电子浓度升高,致使传感器气敏电阻减小[5]。相同温度的同一湿度下,随着浓度的升高,传感器的输出电压也随之增大,但是在不同湿度下,输出电压的增长与浓度的增加关系是非线性的。不同湿度下,相同输出电压对应不同的浓度,浓度和输出电压关系非线性,这给浓度测量带来不便。为提高精确度,应采用补偿方式减小湿度干扰。

2 算法原理

2.1 BP神经网络

BP 神经网络一般由输入层、隐含层和输出层三部分构成,如图1所示。训练样本经输入层进入网络,在隐含层和输出层对样本数据进行训练,更新其权阈值。

图1 BP神经网络结构

1)正向传播算法

输入的样本,从输入层经过隐含层逐层进行处理,通过所有的隐含层之后,经由激活函数传向输出层。输出层将实际输出和期望输出进行对比,如果实际输出与期望输出有偏差,则进入反向传播过程。

假设输入层节点为m个,隐含层节点为q个,输出层节点为n个,输入层与隐含层之间的权值为wji,隐含层的激活函数为f1(·),隐含层到输出层之间的权值为wkj,输出层的激活函数为f2(·),则隐含层中节点输出为

(1)

输出层节点输出

(2)

这样BP网络即完成了从m维空间向量对n维空间的近似映射。

2)BP算法

(3)

对于p个样品,全局偏差为

(4)

为减小误差,把误差信号按原来正向传播的路径反向传回,调节隐含层中的各个神经元的权值系数,让全局偏差信号E趋向于最小。

学习过程中,标准BP算法对所有的权值使用一个统一的学习速度,每步的长度与其方向斜率成比例,其权值更新的基本公式[6]为

ΔWkj(n)=η·G(n)

(5)

式中η为步长参数(即学习速率);ΔWkj为第n次权值修正量;G(n)为当前误差函数对权值的梯度,α为动量因子,n为迭代的次数。由于BP只用局部梯度信息,故η值必须很小,从而使该算法跳过极小值,这使得学习收敛速度变慢,为加快收敛速度,常用的方法是加入动量因子,其权值更新式为

ΔWkj(n+1)=α·ΔWkj(n)+α·η·g(n)

(6)

式中α为动量因子,用来作为减小阻尼局部振荡的量,且动量因子一般在0.9附近。

为提高网络训练速率,避开陷于局部的极小值的不利情形,达到拟合标准等要求,提出了改进BP算法的方法:运用Levenberg-Marquardt法作为训练方式,优化标准BP神经网络,适当调节学习速率和动量因子,使改进的BP神经网络收敛更快,均方误差更小。

但是,BP神经网络在进行训练的过程中,存在训练时间过长,易陷入局部最小值等不足之处。针对这一问题,本文使用GA,对BP神经网络训练过程进行优化,以减小迭代次数与训练时间。

2.2 GA优化BP神经网络

GA是一种基于基因遗传学法则和自然选择的全局搜索方法,其本质是选择—交叉—变异算子的循环过程,直到找到最优结果或者满足终止条件。该算法可得出BP神经网络的最合适权阈值,提高模型预测精度。

本文设计的 GA-BP神经网络算法在 MATLAB上实现,算法主要流程如下[7,8]:1)初始网络拓扑结构,初始神经网络权阈值长度,GA对初始化编码,得到初始种群；2)设计适应度函数,用适应度函数计算染色体适应度；3)进行选择、交叉和变异操作产生新的种群；4)达到终止条件,获取全局最优的网络权值和阈值,否则返回上述步骤(3)；5)代入最佳权阈值,进行BP神经网络的训练,从而得到全局最优解。

依据GA的特性设计参数,其中种群大小设置为10;染色体采用二进制形式编码,交叉概率为0.7,变异概率为0.08,进行调节参数[9]。

3 基于气体传感器的神经网络湿度补偿

3.1 基本测试电路

基本测试电路如图 2所示,Vh为加热电压,VC为工作电压,VO为输出电压,RL为负载电阻。

图2 基本测试电路

3.2 气体传感器试验数据标定

利用神经网络拥有复杂的非线性映射、自组织、自学习及推理能力的特性,结合GA对传感器进行湿度补偿。要达到上述目标,首先要对神经网络进行训练,训练样本由实验数据提供。实验所用传感器是二氧化锡(SnO2)为主要材料的异丙醇气体传感器,工作电压为10 V,加热电压为4.5 V,通过控制变量法测试。以60 %RH,24 ℃条件为标准,计算未补偿时与标准值之间的误差百分比如表1所示。

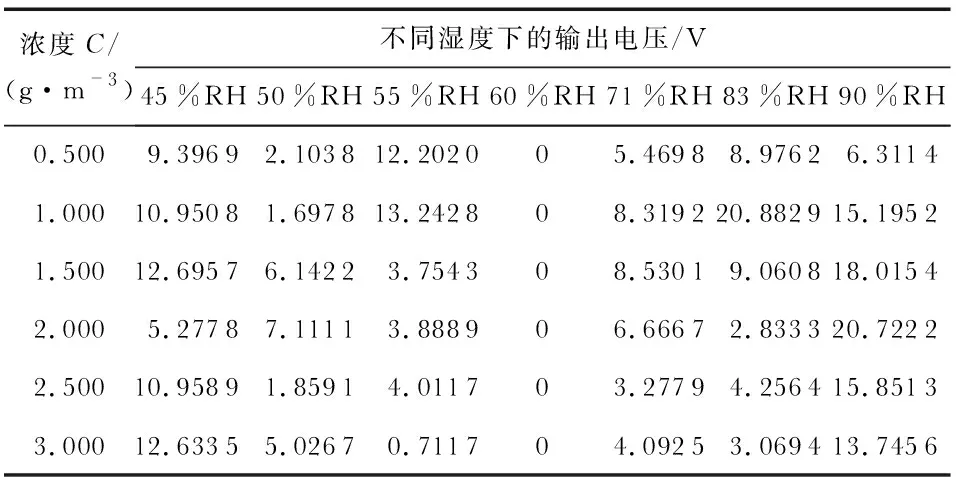
表1 不同相对湿度下气体传感器部分测试结果未补偿时误差百分比

为了使神经网络更好地运算,将样本数据输入网络之前,首先进行归一化处理[10],如下

(7)

(8)

3.3 仿真研究和结果

使用 MATLAB 2017的BP神经网络工具箱及MATLAB自带工具箱对数据进行处理[11]。采用 BP算法对样本进行训练,输入层设1个节点,隐含层选5个节点,隐含层的个数不固定,输出层设为1个节点。输入向量的范围是[0,1],隐含层采用Losig函数,输出层采用 Purelin函数,网络训练函数为Trainlm。设置训练目标误差为0.000 01,最大训练次数设为3 000次,将样本库数据,经过不断调试,训练神经网络得到期望的预测效果。

使用标准BP神经网络训练湿度环境为45 %RH～90 %RH的样本,样本数为600个数据,预测效果及训练误差百分比,如图3所示,其中绝对误差百分比最大为14.3 %,最小接近0,平均绝对误差百分比为5.7 %。

图3 BP神经网络预测绝对误差百分比

通过实验增大训练数据,调节参数改进BP神经网络进行预测,预测结果效果得到改善,样本预测最大绝对误差百分比为13.2 %,平均绝对误差百分比为3.04 %,绝对误差百分比在3 %以下比较集中,大于4 %的部分偏差较大,对整体预测效果有较大影响。

采用GA对BP神经网络优化,预测绝对误差百分比如图4所示,最大绝对误差百分比为7.2 %,平均绝对误差百分比为1.96 %,大部分绝对误差百分比分布在3 %以下,且预测误差小于1 %的比重大,使不同的湿度下输出结果波动减小,提高整体预测准确度。

图4 GA-BP预测绝对误差百分比

3.4 算法补偿效果分析

计算改进BP网络和GA-BP网络的训练数据,可得到表2的数据结果。

表2 神经网络训练结果

由于气体浓度不同时,测量输出电压不同,在输出小电压时小的误差引起的误差百分比较大,使绝对误差百分比分布有波动,使用平均绝对误差百分比作为衡量预测效果的指标,通过实验室测试增大数据和改进BP神经网络提高预测精度。对比表2中的数据可知,使用GA-BP网络算法比使用BP神经网络的平均绝对误差百分比减少65.6 %,比使用改进BP算法的平均绝对误差百分比减少35.3 %,均方根误差为0.035 6波动小。

4 结束语

通过改进BP神经网络和结合GA优化BP神经网络的方法,减小不同环境湿度对传感器输出的影响,得到准确的输出结果。测试结果显示,使用GA优化BP神经网络,平均预测误差百分比降为1.96 %。GA-BP网络算法预测误差百分比与标准BP算法和改进BP神经网络相比,分别减少65.6 %,35.3 %,波动小稳定性更好。使用GA-BP网络算法使传感器的测量准确性和湿度可靠性得到有效的提高,改进算法对传感器输出性能有提高。在后续的研究中,将拓宽温湿度测试范围,并进一步优化算法,提高异丙醇气体浓度检测的精度。