基于超声波传感器阵列的空间感知方法*

陈炳舟, 孙万林, 陈立平,2

(1.塔里木大学 信息工程学院,新疆 阿拉尔 843300；2.塔里木大学自治区教育厅普通高等学校现代农业工程重点实验室,新疆 阿拉尔 843300)

0 引 言

基于多传感器信息融合的空间感知方法研究,具有广阔的应用。例如雷达感知及全球定位系统(global positioning system,GPS)定位技术的空间信息融合感知应用,被广泛应用于机器人导航、自动驾驶、地质勘探等领域。超声波传感器也是一种重要的空间感知手段,相较于视觉空间感知技术而言,超声波感知技术受光线、烟雾、电磁干扰等因素的影响较小。但单个超声波传感器只能测量到物体表面某点的距离,无法快速采集物体表面多个区域的距离信息[1]。针对单个超声波传感器空间感知的不足,启发了利用多个超声波传感器组成超声波传感器阵列采集距离信息,通过坐标变换融合到同一坐标系下形成点云的空间感知方法。

1 相关工作

从应用场景而言：2021年，牛昊东等人[2]运用超声波传感器设计了风速和风向双参数的检测系统,并和ZRQF型铂电阻丝式风速传感器进行了对比测量,验证了其精度。2020年，李明法等人[3]将超声波传感器测距及CCD相机光流法技术融合构建了智能小车障碍物检测系统,为路径规划提供较好的环境感知基础。2017年，王志春等人[,4]以铝合金液位为实验对象,研究了热气流和温度对超声波测距传感器检测铝合金液位的影响,实验结果表明,热气流对带有温度补偿的超声波传感器测量结果影响大。2014年，韦兴平等人[5]总结了超声波传感器的重要应用有测距、自动焊缝跟踪、流量测量、液体浓度检测、零件无损探伤等。

从多超声波传感器测距而言：2021年，王毅等人[6]使用超声波传感器阵列搭建小车跟随系统,通过实验验证了系统具有行驶误差小、实时性高、运行稳定的特点。2019年，朱小会等人[7]使用多超声波传感器设计了一种轴承形廓质量自动检测系统,并通过实验表明了自动检测技术显著提高了轴承形廓质量检测的效率。2017年，辛喆等人[8]采用8只超声波传感器组成超声波传感器阵列对车辆周围目标物进行识别,通过仿真实验结果表明该方法具有一定的可行性。

从点云数据处理而言：2021年，王博等人[9]运用RANSAC算法结合特征线提取算法对点云进行处理三维重建,提高了测量效率。2021年，赵传等人[10]结合区域增长和RANSAC算法对机载激光雷达(LiDAR)采集的屋顶点云数据处理,实验结果说明,该方法可以有效分割不同复杂程度的建筑物屋顶面,为点云精简提供可靠信息。2020年，管郡智[11]利用激光雷达采集空间几何信息形成三维点云，然后运用RANSAC和最小二乘结合的方法来进行地面点云的检测和滤波，为无人驾驶系统提供环境感知能力增加系统的安全性。2020年，吉文来等人[12]提出了一种基于混合整体最小二乘的曲面拟合方法,提高了复杂区域的点云滤波精度。2019年，唐泽宇等人[13]使用加权最小二乘法拟合生成曲面,并计算曲率,实验表明，其可以有效提升曲率计算的准确度,避免孔洞现象。

本文采用多超声波传感器作为点云数据采集装置,运用RANSAC和最小二乘的方法处理点云数据,提出基于超声波阵列的空间感知方法。

2 超声波阵列空间感知整体设计

2.1 总体设计

系统包含两大部分：信息采集部分、上位机部分,其中信息采集部分由空间感知器和旋转载物台组成,上位机包含点云可视化及点云拟合的功能。首先将被测物体放置在旋转载物台上,使用由超声波阵列组成的空间感知器采集到被测物体表面的距离信息；然后使用PC作为上位机接收、处理数据；最后通过点云拟合输出拟合图形和图形参数,据此感知被测物体距离、外形信息。总框图如图1所示。

图1 超声传感阵列空间感知处理框架

2.2 超声波传感器阵列设计与校准

超声波测距精度受声速影响且量程与发射角和发射频率有关,为保证空间感知系统的响应速度及测距精度,要求超声波传感器量程不大于5 m。因此,选择测量范围为0.02～4 m发射频率为40 kHz的US—015型超声波传感器,它测距精度可达0.5 mm,且重复测量一致性高。参考激光雷达的机械扫描和阵列探测的两种工作方式,根据被测物体的外形以及点云成像原理设计了超声波排列方式。

超声波阵列采用延时顺次控制的方式工作,由STM32控制超声波阵列测距周期与时间间隔。US—015型超声波传感器收到激活脉冲时,接收端口产生高电平,当收到回波时停止高电平。STM32单片机要准确获取这一段高电平所持续的时间,通过公式换算成距离,故通过STM32单片机自带的定时器输入捕获通道来检测高电平持续时间。超声波传感器的Echo输出端引脚和单片机设定的定时器输入捕获通道对应的引脚相连接,分别为PD10～PD15。发射端Trig接收到至少10 μs的高电平信号就会工作,故与STM32任一IO口连接都可以,这里选择PC4～PC9。各超声波传感器与STM32控制器的电路连接方式如图2(a)所示。

为防止超声波阵列测量误差较大,需要对各超声波传感器进行校准。将超声波阵列基座嵌入一块MPU6050陀螺仪传感器,通过陀螺仪保持超声波阵列基座处于水平,把各超声波传感器放入阵列基座中,在其下方放置一水平面,使各超声波传感器测量到水面的距离最小后固定各超声波传感器。校准原理示意图如图2(b)所示。校准后的超声波阵列实物图如图2(c)所示。

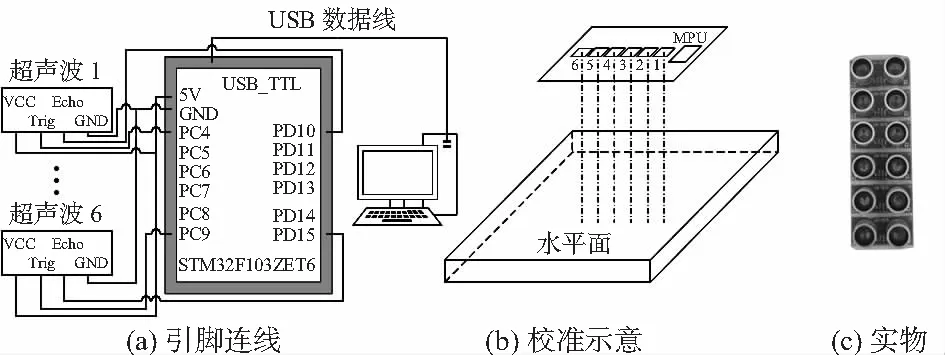
图2 超声波阵列

2.3 超声波传感器阵列数据采集与数据处理

超声波传感器是紧密排布的,存在一定的干扰问题,故采用循环激活的方式让各超声波传感器依次工作,按顺序给每个超声波传感器发送触发命令采集数据来解决各传感器间的干扰问题。使用单片机自带的定时器中断获取时间t,考虑到中断的特殊性,每一个超声波传感器激活函数间要加延迟函数。延迟测量最大距离所用时间,确保上个超声波已经进入了中断,待上个测量完成后才能开启下个超声波的测量。否则两个测量信号都发送出去,外部中断会依次触发执行先收到触发信号的中断服务函数,另一个中断会等到当前中断执行完毕之后才会进入。此时后面信号的高电平时间可能很小或没有,因而收到的数据会显示0或较小的数值。通过当前环境下的声速v,通过公式S=vt/2计算出超声波传感器到被测物的距离。测距原理示意图如图3(a)所示。当STM32核心控制器将采集到的信息转换为距离信息后,通过STM32单片机自带的CH340USB转串口芯片,通过USART串口将距离信息传输给PC。PC接收到距离信息后将其转化为三维坐标,以下为转化原理。

平面测量时,以1#超声波传感器为相对坐标原点。超声波传感器阵列每次采样时,测量距离为各点x坐标,平面相对初始时刻位移距离为y坐标,其他超声波传感器相对于1#超声波传感器的空间距离为各采样点的z坐标。

曲面测量时,以1#超声波传感器为相对坐标原点,将被测物体放旋转载物台上。各采样点的z坐标为其他超声波传感器相对1#超声波传感器的空间距离。超声波传感器阵列每次采样时,测量距离为此时刻各采样点的x坐标,y坐标为0,下一时刻随着旋转载物台的转动,上一时刻的各采样点发生转动,通过坐标变换的方法计算出各采样点的最新坐标(XYZ)。具体计算公式如下

[x′y′ 1]=[xy1]×

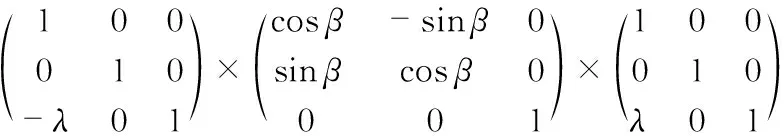
(1)

以1#超声波传感器为相对坐标原点建立如图3(b)所示空间直角坐标系,x′,y′为超声波阵列之前某一时刻各采样点在当前时刻的X,Y坐标,x,y为之前采样点初始的X,Y坐标,β为采样时到当前时刻旋转载物台所转过的角度。

图3 超声波阵列数据处理原理

2.4 点云拟合算法

2.4.1 最小二乘法拟合点云

最小二乘法简单来说就是要求所有点的误差平方和最小,也就是所有测量点到真实面的距离的平方和最小。首先给定欲拟合面的数学模型,求出所有点到此数学模型的距离,将其平方后求和,运用求偏导的方法求解当平方和最小时数学模型的所有参数。具体计算公式如下所示,以平面为例：拟合平面的方程为

z=a0x+a1y+a2

(2)

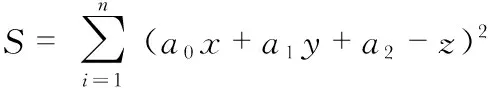
(3)

解上述线性方程组,计算出待定系数a0,a1,a2,可得拟合平面。柱面和球面最小二乘拟合求解同理可得。但是,最小二乘法照顾到了所有的点,若样本点中有过多的坏值就会影响到拟合的结果。

2.4.2 RANSAC算法点云拟合

首先从点集中随机的选出一组样本点,样本点的个数要求要保证能够求解出模型的所有参数,得到一个样本模型。以平面为例,选取3个随机点,P1(x1,y1,z1),P2(x2,y2,z2),p3(x3,y3,z3),代入平面方程z=a0x+a1y+a2,计算出a0,a1,a2,计算其他点到样本模型的距离。如果距离在设定的阈值范围ε内,则认为其是内点,否则为外点,保留内点个数最多的样本模型,并将内点个数最多的样本模型记为最佳模型(best model)。重复以上步骤使最佳模型的内点个数大于等于设定的值或达到设定的最大迭代次数为止,此时最佳模型即为拟合结果。

与最小二乘算法比较,其可以减少超声波传感器采集到的坏值对拟合结果的影响,使得拟合结果更接近实际物体的外形。

3 实 验

3.1 实验设计

为验证基于超声波阵列空间感知方法的可行性及鲁棒性,设计了验证实验,分别用该方法测量平面、柱面、球面,求出距平面的距离、柱面的横截面半径、球面的半径,最终对比手工测量值。选择三个实验对象：一个平板、一个圆桶、一个足球。首先用游标卡尺手工测量圆桶的横截面半径以及球面半径,测得结果：圆桶的横截面半径为50 mm,足球的球面半径为80 mm。

实验时,首先将超声波阵列竖直固定在一处,分别在超声波阵列前20,25,30,300 mm处放置平面并测量,然后把旋转载物台的中心放置在相同的刻度处,将圆桶和足球放在载物台上依次测量,获得不同位置处平面、圆桶、足球的点云数据。使用RANSAC算法和最小二乘算法分别对点云数据进行拟合,求出模型参数,重复上述步骤10次,分析系统的可靠性。实验场景示意图如图4所示。

图4 测量实验场景示意

3.2 实验结果与分析

采用最小二乘法和RANSAC拟合结果如图5所示。

图5 20 mm处测量实验结果

其中,采用最小二乘法拟合平面的平均测量误差为0.6 %,柱面的平均测量误差为2.74 %,球面的平均测量误差为1.713 %；采用RANSAC算法拟合平面的平均误差为15 %,柱面的平均测量误差为2 %,球面的平均误差为4.98 %。

使用RANSAC算法来精简点云提高精度,由图5算法拟合图对比可以看出。RANSAC算法能筛选掉一些误差点然后再进行拟合,但过程中可能会误删一些有用的点,导致拟合结果并没有最小二乘法理想。但随着测量距离的增加,测量误差逐渐增大,RANSAC算法剔除的误差点对精度的提高已经远远超过误删有用点对精度的影响,由表1,表2实验结果可以验证。

表1 两种算法在柱面测量上的效果对比

表2 两种算法在球面测量上的效果对比

实验结果表明:在20 mm处近距离测量时,采用最小二乘算法拟合,三个实验对象的最大测量误差不高于0.6 %,2.74 %,1.713 %。在300 mm到超声波传感器最大量程的距离测量时,可以使用RANSAC算法拟合图形来减小测量误差。

4 结 论

探索了将超声波传感器组合成超声波传感阵列,研究了一种通过超声波传感阵列扫描并构建物体表面轮廓的方法。对物体表面进行密集测距,将采集到的距离信息转换成可视化三维点云；用最小二乘法拟合点云,计算出各实验参数；用RANSAC算法剔除干扰点云并计算实验参数。通过对三个空间实际物体的实验,分析了不同距离、不同拟合方法对实验参数计算的影响,验证了超声波阵列空间感知及其可视化的可行性,同时为视觉测量提供了可验证的物理测量参考。

进一步,将探索超声波传感器阵列空间感知方法与基于双目或多目相机空间感知技术的融合应用。