基于目标识别的机械手定位技术研究*

刘祚时, 穆鸿书, 杨国炜

(1.江西理工大学 机电工程学院,江西 赣州 341000；2.江西理工大学 电气工程与自动化学院,江西 赣州 341000)

0 引 言

单目视觉常常被用于测距、定位识别等,单目视觉定位的方法很多,但如若不借助外在条件很难确定目标的位姿信息。陈金辉等人[1]提出使用单目利用相邻两帧图像进行检测与匹配；祝世平等人[2]采用单目变焦的方法对目标物体进行定位；任沁源等人[3]利用SIFT方位改变但局部不变的特征对连续两幅图像中目标进行匹配,提取目标特征点,并稀疏三维模型来进行定位。

虽然双目视觉定位与人眼最为接近,但是双目没有任何几何约束,两个镜头的误差会造成目标定位不准的不良后果,而且镜头误差的减小带来成本会是几何倍数的增加。因此，展开对单目视觉定位精度和实时性究对机器视觉系统的完善相当有意义。

本文在目标识别方面采用改进后的Harris角点检测,在原有的Harris角点检测程序中额外添加角点本身性质的判别,使得角点的判别条件更加优化,实验结果也证明了其优越性能。

1 桌面机械手数学模型的建立

本文的实验平台由计算机、五自由度桌面机械手、互补金属氧化物半导体(complementary metal oxide semiconductor,CMOS)相机、相机固定连杆、照明光源以及STM32F4开发板组成。

1.1 机械手关节D-H连杆描述

关节式机械手为底座固定,末端为执行机构,中间则由一系列连杆和旋转、平移关节通过串联而形成的开放式链接。为了能够得到相邻连杆之间的联系,由刚体旋转、平移分析所启发,在每个连杆上都固接一个坐标系用来得到机械手运动方程。本文参照Denavit J和Hartenberg R S[4]提出的D-H模型,以4×4齐次变换阵来阐述连杆与连杆之间的关系。使用上述D-H连杆表示法构建本文所用的视觉引导机械手的连杆坐标系关联。

(1)

式中qi为第i个关节变量,对于旋转关节i,qi=θi；对于移动关节i,qi=di。

1.2 蒙特—卡罗法求解机械手关节工作空间

本文采取用随机概率的数值算法—蒙特—卡洛法求解机械手的关节空间。而机械手末端的执行器轨迹规划也是在工作空间内完成[5]。舵机在设计时就确定了关节转角范围,因此,舵机串联后机械手的关节工作空间就确定了。工作空间的规定决定了机械手操作范围。

1)第一步由机械手运动学正解推导机械手末端位置

px=c1a1+d5c1s234+a2c1c2+a3c1c23

py=s1a1+d5s1s234+a2s1c2+a3s1c23

pz=H+d1-d5c234+a2s2+a3s23

(2)

2)在规定的1～4关节限制转角量范围内进行随机取值,随机取值函数由软件自带的rand函数产生

(3)

3)将式(3)中4个关节随机变量取值{θ1,θ2,θ3,θ4}代入式(2)中求出机械手末端位置。

4)设置迭代次数为20 000次,依次在仿真软件中描绘出关节工作空间云图。

图1 视觉引导机械手连杆坐标系

在MATLAB平台设置机械手各关节初始位置

{θ1=π/2,θ2=0,θ3=0,θ4=π/2}

迭代次数设置为20 000次后,形成的机械手关节工作空间云点图如图2 所示,图中,灰点为机械手可到达的位置,机械手未能达到的点称为盲点。程序中未用到关节5和关节6其转角都设置为0。

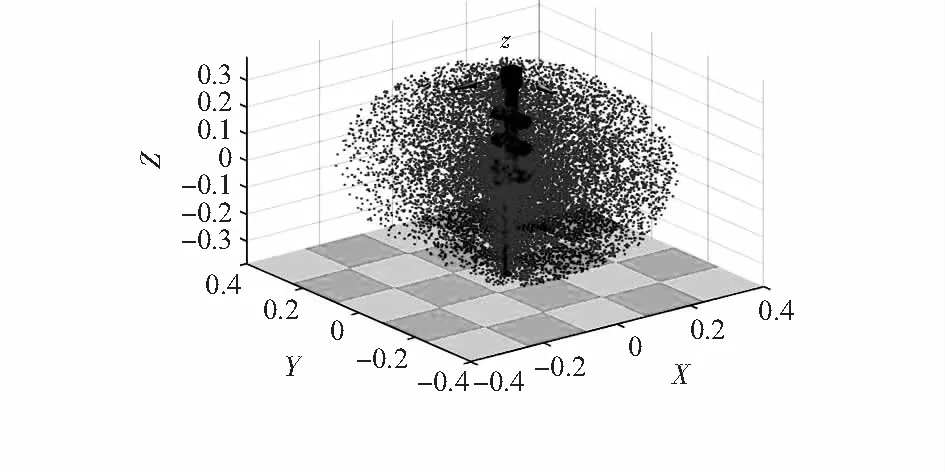
图2 三维空间机械手关节工作空间云点图

1.3 三次多项式插值法的关节空间轨迹规划

三次多项式插值函数包含4个变量约束,即起始关节位置、终止关节位置、起始速度和终止速度[6],根据这四个变量约束来计算轨迹函数系数。经过具体实验验证三次多项式插值法基本能满足机械手运动的稳定性[7]。

设关节角位移相对于时间变化的三次多项式插值函数为

θ(t)=a3t3+a2t2+a1t+a0

(4)

设置初始时刻ts=0,终止时刻为te=3 s,机械手起点位置θs和终点位置分别θe,分别可以得到起止时刻关节的起点速度和终点速度s，e以及起点加速度和终点加速度(ts),(te)得到式(5)

(5)

实际的机械手轨迹规划中是多段点对点运动,此时三次多项式插值法由于没有限制各段之间的衔接条件,所以各点的速度曲线没有平滑地过渡,进而在加速度上没有连续。在实际设计时,应考虑对机械结构的冲击和各个点对速度、加速度的要求选择合适的插值方法。本文就机械手末端点到点的运动采用三次多项式插值方法仿真结果如图3所示。

图3 机械手仿真结果

2 基于单目视觉目标识别与定位

2.1 图像分割

最大类间方差法基于最小二乘法原理推导出来的[8]。其原理是设定一个初始阈值将图像分成两块不同灰度值的目标前景和背景。阈值不断迭代,找到目标前景和背景平均灰度值的标准差最大时,当标准差最大的时就是所要确定的阈值[9]。

设输入图像的矩阵为I(x,y),预设分割阈值设为T,依赖目标前景的像素点的个数占全部分图像的百分比,记作ω0,且前景平均灰度为μ0；属于背景像素点的个数占全部图像的百分,记作ω1,且背景平均灰度为μ1。图像的总体平均灰度记作μ,类间方差记作g。假设图像的整体背景较暗,图像尺寸大小为M×N,灰度值小于T的像素个数记为N0,灰度值大于T的像素个数记为N1,则有

μ=ω0×μ0+ω1×μ1

(6)

g=ω0(μ0-μ)2+ω1(μ0-μ)2

(7)

对于全局自适应阈值和类间方差法对比实验,以冈萨雷斯MATLAB第三版第十章中两幅原图(‘noisy_fingerprin’,‘polymersomes’)为实验对象,原图、灰度直方图、二值化图像如图4所示。

图4 全局阈值处理与类间方差法对比实验

由图4两幅图片的直方图可以看出:在灰度直方图由有明显的分开度时,使用全局阈值处理需要迭代的次数很少,第一幅图仅需2次迭代即可完成图像分割任务。而在“细胞”这幅图片中灰度直方图基本呈高斯分布形态,很难找到合适的分离点进而迭代次数增多,且实验效果对比类间方差法差很多。所以,使用类间方差法能都清晰的分离前景和背景,实现目标提取。

2.2 目标识别

图像识别算法用于从背景中抽取感兴趣的目标,在众多的纹理特征中“角点”信息特征明显,其相对于边缘和平坦区域特征是不同的。Moravec角点检测算法中构造误差函数E(u,v)来比较窗口偏移前后每个像素点灰度的变化值,但这种判断方法还是很不方便

(8)

Harris对Moravec角点检测算子作出改良。其一，改良 Moravec算子检测方向局限性考虑窗口在各个方向上的移动；其二，改良Moravec算子的方形窗口而采用高斯函数作为平滑的窗口。这样使得误差函数E(u,v)的响应不容易受到干扰,根据结构张量的行列式值和矩阵迹平方的插值作为判断条件。图5为积木图片角点检测图,其中角点用“•”标出。

图5 积木图片角点检测效果

可以看出,运用Harris角点检测算法角点基本都能检测出来,但正方形木块和平行四边形木块斜对角有两个角点没有检测出来。因此提出改善策略：根据角点本身的纹理特征,角点在边缘上是连续点,离散点的导数定义为差分,角点在8邻域内类型有如下两种,其他均为图6这两种类型分别旋转45°得到。

图6 带有阴影的角点8邻域类型

由于边缘点和角点都属于边缘灰度值是一样的,故差分结果等于0,而阴影点角点和边缘点都存在灰度插值,故在角点8邻域内只要统计这四个差分值0的个数既可以判断是否为角点。图像附带有阴影对Harris角点判断依据改进后,角点判断的充要条件增加为3个即要满足阈值,同时要满8邻域内极大值点,又要满足8邻域内四个差分值的个数最多不超过一个。如图7为改进角点判断后的Harris角点检测效果图,可以明显看出所有角点均标出,没有漏检。同时,改进后的Harris角点算法对图像的旋转、以及其他噪声的干扰都具有一定的鲁棒性。

图7 改进角点判断后的Harris角点检测效果

2.3 三维目标定位实验

本实验的实验对象在世界坐标系的位置关系如图8所示,左上方正方形积木块和下方正方形积木块以及右上方长方形积木块，分别在表面涂上已知距离关系的标志点替代贴标机动作。

图8 涂上点标志的目标

在图像预处理过程中,提取原图像中通道即可选取长方形的积木块,如图9(a)中是对左上方正方体积木块进行一系列的图像处理技术后形成的二值化图像,其中包含目标物体的边缘直线和四个标志点圆曲线,对于不是圆形的规则物体可以利用特征点为封闭圆弧的特征加以区分,判断条件为每个像素的8邻域内I(xi,yj)-I(xi-1,yj)≠0&I(xi+1,yj)-I(xi,yj)≠0&I(xi,yj)-I(xi,yj-1)≠0&I(xi,yj+1)-I(xi,yj)≠0 共同满足这四个条件即为圆边界,自此可以得到如图9(b)所示的人工标志边缘图。

图9 图像预处理结果

遍历整幅图像可以分别得到每个圆的横轴和纵轴的最小值最大值,任取其中的一点(xk,ym),xmin≤k≤xmax,ymin≤m≤ymax,分别计算圆上每个像素到这个点的距离的平方和,不断迭代求出最大值即为圆的中心点,得到如表1所示的四个人工标志的中心点和目标质心,相机安装高度为470mm。正方体实际边长为29.4mm。

表1 定位数据

由表1中可以验证物体的实际边长为470 mm-443.326 mm=26.674 mm与实际高度相差了3 mm左右,求得目标欧拉角如下

(9)

式中φ,θ,ψ分别为描述物体位姿的RPY角,记为横滚角、俯仰角、偏航角。

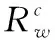
(10)

对左上方正方形积木块进行有序、有目的摆放，得到10组真实目标位置和姿态,利用上述识别定位算法估算目标位置和姿态并与真实位姿相对比。从图10中的误差结果中可以分析得到Z轴方向上的位置平均相对误差7.096%,Φ偏航角姿态估计平均相对误差19.58%。因为摄像头固定安装在正上方,所以，除了Φ角，其他两个姿态角基本都不变。综合实验得到的数据,在非精密制造领域可以实现快速对目标进行识别和定位。

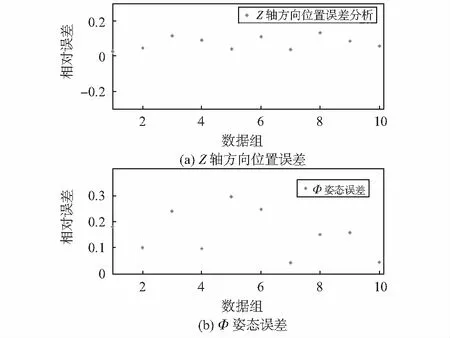
图10 误差结果分析

3 结 论

本文提出了一种采用Eye-to-hand方式固定安装摄像头,并实现单目视觉引导的五自由度机械手定位方法。研究的重点是如何利用单帧图像实现高精度、高时效的定位,进而展开单目视觉在非精密快速准确定位的研究。实验结果表明：目标深度和Φ角度平均相对误差都比较优秀,能够满足机械手非精密定位要求。