多种数值插值算法插值性能分析及优化

张增磊 吕达 赵灯 张强

(1、武汉第二船舶设计研究所,湖北 武汉 430000 2、武汉大学,湖北 武汉 430000)

考虑到强耦合过程的费时、费力、不经济，目前多体或多场之间的耦合多属于弱耦合问题。每一次完成弱耦合都需要对耦合面数据进行插值，达到耦合面数据交互的目的[1]。为了寻求更高的插值精度和插值效率，广大学者提出了大量的插值算法，大致可以分为两类[2]：函数插值法和投影插值法。函数插值法是直接在高维空间构建插值函数来传递耦合数据的一类流固耦合数据传递方法，包括最邻近点插值法[3-4]、加权余量法[5]、基于径向基函数(RBF)的插值法[6-7]、样条函数法[8]等。投影插值法是先将待插值的网格节点以某种方法投影后再构建插值函数传递耦合数据的一类流固耦合数据传递方法，包括映射点插值法[9]、常体积转换方法[10]、载荷面法[11]、定义局部坐标[12]和引入数据降维方法等距映射法ISOMAP[13]。

为了实现耦合面之间压力的准确传递，本文针对最临界点插值法、最小二乘插值法和等距映射法，利用数据计算，分析了网格数目、网格质量和耦合面边界类型对插值精度和插值效率的影响规律，并提出了一种基于网格循环的插值策略，当耦合面采用高阶单元时，可以提高耦合面插值效率，对耦合面总压力的传递具有较高的准确率。

1 三种常见的数据插值算法

1.1 最邻近点插值法(NN)

最邻近点插值法(NN)实现方式较为简单，通过对耦合面网格所有节点进行遍历，将距离最近的节点载荷数据作为待插值节点的载荷数据。

为获取待插值点M(x， y， z)的载荷数据，通过式(1)获取该节点与源耦合面节点M′(xi， yi， zi)的距离

m 为源耦合面最大节点编号。若节点i 的载荷数据为N(xi，yi， zi)，则节点M的载荷数据为N(xi， yi， zi)。

1.2 最小二乘多项式插值法（L2）

通过选取与待插值点M(x， y， z)临近的k 个节点的载荷数据，构建如式(3)所示的多项式进行数据插值，获取待插值点的载荷数据。

首先，依据源耦合面内k 个临近节点构建载荷矩阵方程P=AB，其中

1.3 等距映射法（ISOMAP）

等距映射法是基于多维尺度分析(MDS)的非线性降维算法，可以消除耦合面空间非线性对耦合数据传递的影响。该算法先采用邻域欧式最短距离估计点与点之间的距离，然后应用多为尺度分析计算在和数据的低维插值载荷数据。该过程的实现可分为以下三个步骤。

（1）构造邻域图。若源耦合面内节点总数为N，采用K- 邻域判断源耦合面内任意两节点(i， j)是否相邻，若相邻，则确定节点距离d(i， j)，并最终构建邻域图G。

（3）构建d 维插值。对矩阵Dm应用MDS 算法构建最小化目标函数

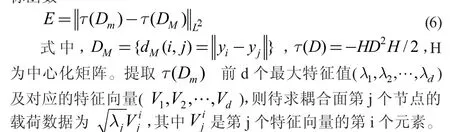
2 三种插值算法的插值性能分析

如图1 所示，本文拟定两个物理场的耦合面尺寸均为100mm×100mm，源耦合面网格节点均匀分布，而待求耦合面的网格节点依据给定的平均单元尺寸均匀分布或自由生成。通过对比最邻近点插值法、最小二乘多项式插值法和等距映射法三种插值算法的插值计算时间、插值误差进行对比，分析了不同耦合面网格尺寸、网格质量和耦合边界类型对三种插值算法的插值效率和插值精度的影响。

图1 耦合面节点分布示意图

2.1 网格尺寸

在分析单元尺寸对插值计算的影响时，本文设置待求耦合面采用网格自由划分方式，更改耦合面单元尺寸，耦合面节点数据如表1 所示。

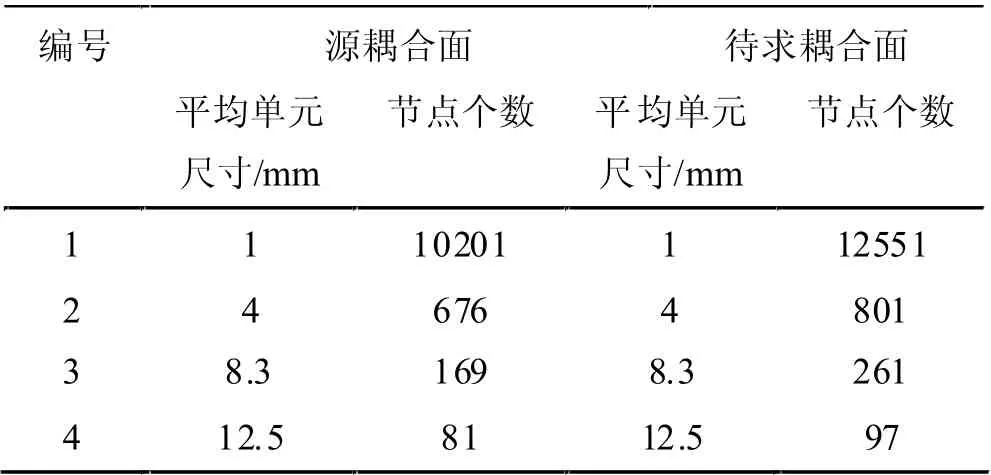
表1 耦合面网格尺寸设置

最邻近点插值法、最小二乘多项式插值法和等距映射法三种插值算法的传递的总压力和插值时间如图2 所示。

图2 网格尺寸对插值效率和插值精度的影响

当两个耦合面单元尺寸相近时，改变网格尺寸，插值时长与耦合面节点在对数坐标系下呈现正相关，即T∝Nk。对于三种插值算法，指数k 分别为1.97，2.05，2.14。最邻近点插值法在整个插值过程中，包含两类循环：一种是对待求耦合面所有节点进行循环，获取每个节点的压力值；另一种是对源耦合面所有节点进行循环，获取源耦合面内待求节点的最邻近节点。而第二种循环中嵌套在第一种循环中，导致了该算法的系数k 接近2。而最小二乘多项式插值法和等距映射法并不仅仅依靠最邻近节点的压力值而确定，会根据临近多个节点进行拟合，获取待插值点附近的更加准确的压力分布，导致插值效率均低于最邻近点插值法。

最邻近点插值法在求解每个节点压力时由较大误差，导致了计算所得的总压力大于源耦合面的总压力，通过折算降低节点数目不等带来的误差后，最大误差仍可达到34.9%。由于该插值算法中耦合面各节点互不干扰，独立计算，当节点个数多于源耦合面节点数时，多出的节点必然会增加耦合面的总压力。最小二乘多项式插值法也存在类似的不足之处。当节点数较少时，源耦合面节点承受的压力远高于节点数多的情形，多出的节点数目对总压力的计算影响较大，导致了传递的总压力随着节点数的增加而呈现先增大或降低的趋势。而等距映射法会构建邻域图，节点之间会相互影响，减弱多出的节点对计算的影响，插值精度也会随着节点数目的增加而缓慢增加，但仍会增大传递的总压强。

若以式(7)获取的待插值点处压力为准确数据，则第三组所有插值点的相对误差如图3 所示。

图3 待插值节点压力误差

由图3 可知，三种插值算法均能保证每个节点的相对误差小于2%，但最邻近点插值法的插值精度明显弱于最小二乘插值法和等距映射法。对于同一套网格，利用三种算法计算的节点压力的相对误差的分布基本一致。由此图可以推断，网格质量或者节点分布均匀性对插值精度具有显著的影响。若降低耦合面节点数目，必然导致源耦合面节点之间梯度变大，会加剧插值点的相对误差，特别是对最临近点插值法。

2.2 网格质量

为了研究耦合面节点的分布对插值过程的影响规律，在耦合面节点数目相同的基础上，选定了三种待求耦合面节点分布，网格质量从左往右依次增加，示意图如图4 所示。在源耦合面上施加式(7)所示的压力，三种插值算法的插值时长和耦合面总压力如图5 所示。提下，等距映射法插值效率最低，最邻近点插值法插值效率最高，高于等距映射法的两倍。

图4 不同网格质量的待求耦合面节点分布

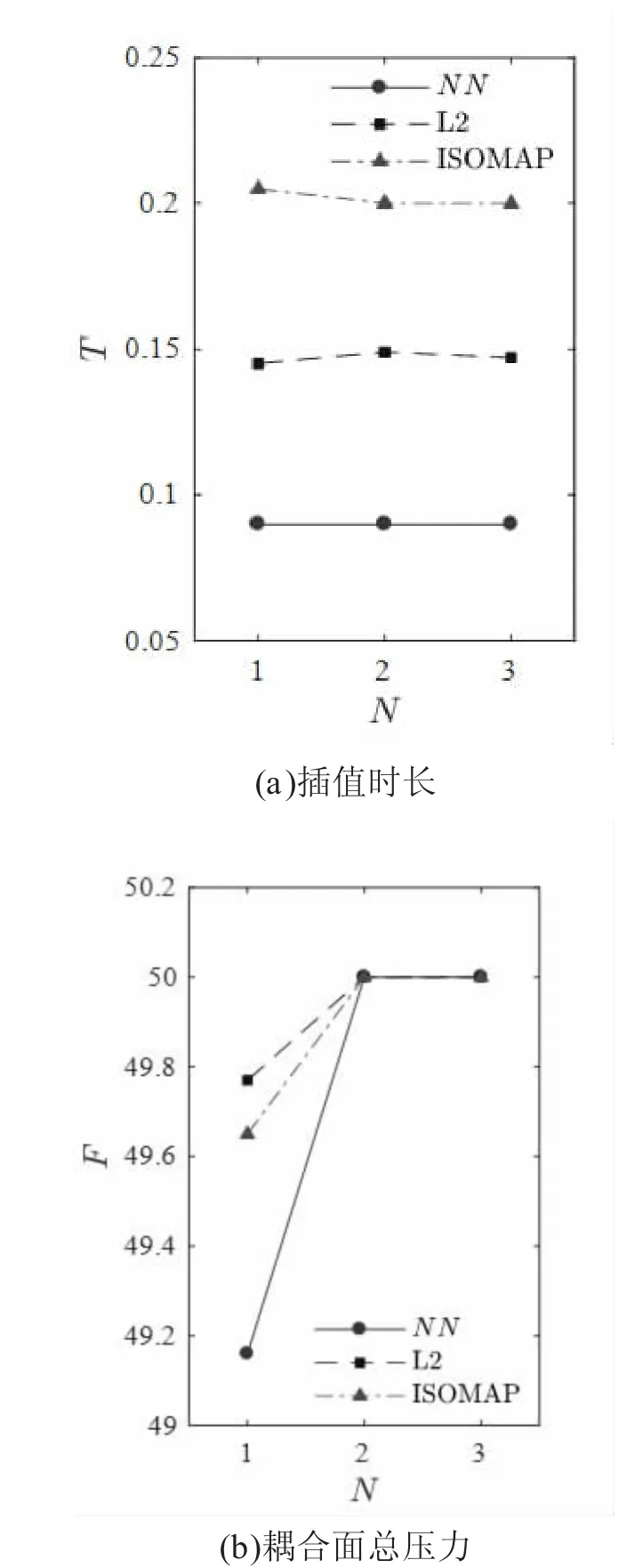
图5 网格质量对插值效率和插值精度的影响

由图5(b)可知，质量较高的网格可以提高插值精度。在提供的三种网格中，三种插值算法仅对网格1 产生较大的插值误差，大小分别为1.68%，0.46%和0.70%，而对网格2 和网格3 的插值误差均低于0.01%。

在不同网格质量下，每个节点压力的相对误差如图6 所示，其中网格3 导致了相对误差均为0，则并未附图进行说明。从左往右分别利用了最临近点插值法、最小二乘插值法和等距映射法进行计算。

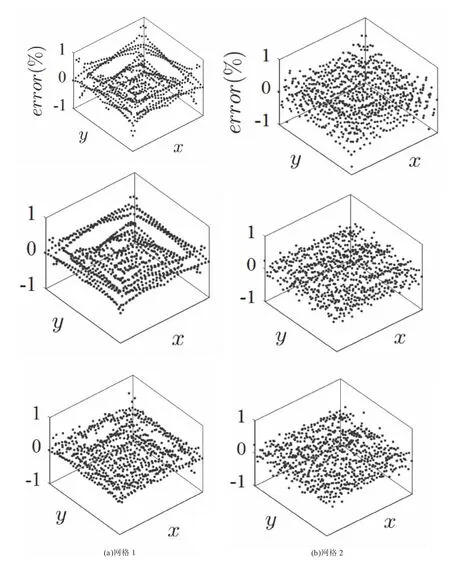
图6 节点插值压力的相对误差

图6 直观地展现了网格质量对插值精度的影响。当网格自由划分时，节点一般会在靠近边界的区域无规律分布，而恰好在该区域，节点的相对误差较大，且变化明显。针对网格2 和网格3，当节点分布较为均匀时，节点的相对误差普遍较小，插值更加准确。

3 结论

本文介绍了三种常见的数据插值算法，分析了网格尺寸、网格质量对插值性能的影响规律，并提出了一种利用网格遍历的插值优化策略，得到如下结论：

3.2 网格尺寸、网格数目对插值精度影响较大，三种插值算法对三种参数的敏感程度也不一致，且三种参数对三种插值算法在插值精度上的影响程度分别是最邻近点插值法、最小二乘插值法和等距映射法。若以压力作为传递参数，耦合面节点数目对传递的总载荷影响较大，待求耦合面节点数大于源耦合面节点数，导致了传递的总载荷增大，增大幅值近似于两耦合面节点数之比。质量高或节点分布均匀的网格，耦合面变化梯度较小均有利于降低整体节点的压力相对误差，提高插值精度。若网格节点数目较少，甚至网格质量不高时，最临界点插值法的插值精度会急剧增高，在本文所计算的数据中，最高可达到34.9%。