基于相对成像时刻编码遗传算法的敏捷成像卫星任务规划
韩 鹏,郭延宁,李传江,李文博,马广富
(1.哈尔滨工业大学控制科学与工程系,哈尔滨 150001;2.北京控制工程研究所,北京 100190;3.空间智能控制技术重点实验室,北京 100190)
0 引 言
敏捷成像卫星是指具有三轴快速姿态机动能力的对地观测卫星,近年来,已成为各国竞相研发的新一代对地观测卫星,目前,已投入使用的型号包括美国的WorldView系列,法国的Pleiades星座以及我国发射的“高景”系列卫星等[1-2]。观测范围广、灵活性强的特点使其获得了比传统的对地观测卫星更高的效率。观测能力的提高也对卫星的管控与任务规划带来了挑战,要想充分发挥敏捷卫星的优势,必须有高效可靠的任务规划与调度系统[3-4]。
相比于非敏捷卫星,敏捷卫星增加了俯仰和偏航两个自由度的姿态机动能力,因此对目标的时间窗口更长,观测、推扫的方式也更加多样。传统成像卫星对目标点的可见时间窗较短,因此其观测时刻固定,而敏捷卫星对点目标进行凝视观测时,由于目标可见时间窗口的增加,不同的成像时刻将对应不同的姿态,在观测序列固定时,成像时刻的变化会导致观测序列对姿态转移时间约束的满足性发生变化,从而导致观测收益和观测能耗的变化。并且,对于时间窗口重合的目标点,观测时刻的变化也会导致观测序列的变化。观测序列与成像时刻的互相影响与耦合为任务规划与调度问题的建模与求解带来了较大困难。
近年来,国内外许多学者都针对敏捷成像卫星的任务规划调度问题展开了相关研究。一些用以描述敏捷卫星任务规划问题的数学模型相继提出,例如基于“逻辑约束”的背包模型[5],整数规划模型[6-7],基于复杂网络理论的规划模型[8],混合整数规划模型[9-10],约束满足模型[11-12]等。以上文献的规划模型中大多只考虑了时间窗口增加而带来的观测序列多样性,却鲜有考虑成像时刻和姿态转移方式对任务收益及卫星资源变化的影响,只将观测序列或每个目标点是否被观测作为决策变量的模型对问题的描述是不够完整的。另外,卫星在对多点目标进行连续观测时,需进行快速姿态转移,不同目标间姿态转移时间约束是任务规划问题中必须考虑的一项关键约束条件[2]。然而,已有研究一般将卫星姿态转移时间约束视为匀速运动,姿态转移要么保守性强,要么可能导致观测任务无法按照规划结果完成。因此,赵琳等[13]基于卫星姿态运动模型,以时间最优为指标,利用高斯伪谱法完成对姿态转移时间约束的检查,但其在规划模型建立时主要基于旅行商问题模型,需保证待观测目标点全部观测,不能对目标点进行选择和取舍。针对该问题,文献[14]基于动态旅行商问题建立了任务规划模型,但仍未考虑长规划周期下,卫星对目标点存在多个可见时间窗口的情况。
元启发式算法是一类多用于复杂优化问题中的智能化算法,近年来也被应用于敏捷卫星任务规划问题的求解中,如禁忌搜索[15]、差分进化算法[16]、蚁群算法[14]、遗传算法(Genetic algorithm,GA)[13-14,17-22]等。其中遗传算法由于流程简单,收敛速度快等特性,应用最为广泛。遗传算法求解时,编码解码方式设计以及有针对性的算法改进措施是影响求解结果的关键因素[4]。已有文献中,大多采用符号编码方法,利用基因型表征卫星对目标点的观测序列完成对决策变量的编码过程。该编码方式具有直观易懂,迭代搜索效率高的特点,但无法完成对观测时刻的搜索优化,在解码时通常通过一定的规则得到目标点的观测时刻,这可能会使得算法在优化过程中丢失优质解。为此,文献[14]设计了一种将观测序列与观测时刻混合的二维编码伪谱遗传算法,能够同时完成对目标观测序列与观测时刻的优化与求解;文献[19]同样设计了一种将观测时间窗和观测时刻结合的二维杂合编码。通过二维编码可以将规划模型中的观测时间窗口与观测时刻两决策变量同时进行优化,能够保证完整的搜索空间。但二维实数编码方式在交叉、变异过程中容易产生不符合取值约束的染色体,需要设计复杂的约束检查和调整规则,或设计全新的遗传算子,容易导致求解效率降低。
本文同样以遗传算法作为敏捷成像卫星任务规划问题的基本求解算法,并尝试针对上述文献中存在的局限性加以改进。文章的主要贡献如下:
1)在任务规划问题构建中,综合考虑对地凝视成像点目标观测收益与卫星姿态转移期间能耗,构建了卫星任务规划优化目标。特别地,在单次姿态转移过程进行了能量最优化求解。
2)在任务规划问题求解中,提出了一种基于相对成像时刻编码的自适应遗传算法(Relative imaging time coding based adaptive genetic algorithm,RITC-AGA)。通过一维实数编码完成对两个决策变量编码,既可保证对决策变量有完整搜索空间,也能保证在遗传算子迭代过程中不产生不符合取值约束的染色体。利用该编码还可解决长观测周期下卫星对目标有多个时间窗口情况下的任务规划问题。同时,设计了参数自适应变化的交叉和变异算子,可提高算法收敛速度,并使其不易陷入局部最优。
1 敏捷成像卫星任务规划问题
1.1 变量定义
首先对建模过程中用到的参数变量进行定义:
C={c1,c2,...,cn}:待规划目标点集合,ci表示第i个目标,n表示目标点的数量。
lgt_ci=[Bi,Li,hi]Τ:ci的经纬高坐标。
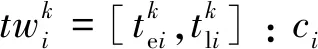
tsi:ci的开始成像时刻。
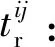
di:ci的观测时长。
wi=Lidi:ci的观测收益,Li为目标观测优先级。
si:ci的观测状态,若si=1代表ci将被观测,si=0表示不被观测。
Q={ci,cj,ck,…}:任务观测序列。
T={tsi,tsj,tsk,…}:任务观测序列Q对应的开始成像时刻,
u=[u1,u2,u3]T:卫星三轴输出力矩。
rs=[rx,ry,rz]T:卫星在地心惯性系的位置矢量。
1.2 任务规划问题构建
任务规划问题构建包含三个元素,分别是:指标函数、约束条件和决策变量。下面进行详述。
1)指标函数
在敏捷卫星执行多目标观测任务过程中,一方面要提升观测收益,另一方面也要降低姿态转移和凝视观测产生的能耗。不失一般性,这里假设cj是ci的后续观测目标。因此,构建如下指标函数:
(1)
指标函数由两部分组成,前一部分表示观测ci所获收益,后一部分表示卫星执行观测任务时的姿态转移能耗,包括卫星由观测ci到cj的姿态转移能耗及卫星跟踪观测目标cj的能耗。κ为能耗代价权重。其中,卫星进行不同目标点之间的姿态转移能耗与各轴输出的姿控力矩及姿态转移时长有关。卫星跟踪观测目标cj过程中的能耗包括卫星姿态凝视跟踪能耗和相机凝视成像的能耗两部分,为简化问题将其设定为与时间相关线性函数。k为其常系数。
2)决策变量
取所有目标点观测状态si及被观测目标点开始成像时刻tsi为决策变量,其中i=1,2,……,n。
3)约束条件
a)卫星轨道动力学约束:
(2)
式中:μ为一常量。考虑卫星轨道固定且已知,在执行观测任务过程中不进行轨道机动。卫星轨道动力学约束通常用于求解卫星在任意时刻的位置。
b)卫星姿态转移控制力矩约束:
|ui|≤um,i=1,2,3
(3)
其中:um为卫星最大控制力矩。
c)卫星姿态转移时间约束:
(4)
该约束由卫星当前位置rs、惯性姿态qs、卫星控制力矩u、cj的经纬高坐标lgt_cj、cj开始成像时刻tsj等因素相关,具体求解方法将在下节详细叙述。
d)相邻任务开始成像时刻约束:
(5)
卫星姿态从指向目标点ci机动至指向cj对cj进行观测时,其姿态转移结束时刻不得晚于预定对sj观测的开始时刻。
e)目标观测时间窗口约束:
(6)
卫星对任意目标点的观测开始时刻必须在其可见时间窗口内。
f)目标观测次数约束:
ci≠cj, ∀ci,cj∈Q,i,j=1,…,n
(7)
上式表示观测序列中任意两个目标点不能相同,亦即每个目标点只需被观测一次。
g)目标观测时长约束:
di≡const,i=1,…,n
(8)
此处考虑每个目标点的凝视观测时长固定,有效观测时长少于预定观测时长则收益为0。
2 目标间姿态转移最小能耗估算
2.1 卫星凝视观测期望姿态确定
考虑卫星在执行观测任务期间无轨道机动,即卫星位置可由约束条件a)唯一确定,同时地球自转角速度恒定,目标点在惯性系的位置[xi,yi,zi]T可通过目标的经纬度坐标lgt_ci经过地心固连系和地心惯性系之间转换得到。因此,由卫星与目标相对位置可得卫星指向目标的期望姿态。
如图1所示,卫星在t0时刻完成对目标点ci的观测,考虑载荷轴沿本体轴z轴指向目标点ci,对应惯性姿态四元数为qs=[q0,q1,q2,q3]T,若获得可行解使得卫星在t1时刻使得本体轴z轴观测目标点cj,因此卫星需在[t0,t1]时段内完成姿态机动。要判断是否能在预定时间完成姿态机动,首先需要确定终端姿态。由于没有观测视角的限制,因此终端姿态只有本体z轴是固定的,x轴与y轴的指向任意,无法唯一确定卫星姿态。因此,以最小化两目标间姿态机动角度为目的,本文设计了一种凝视观测期望姿态确定方法。
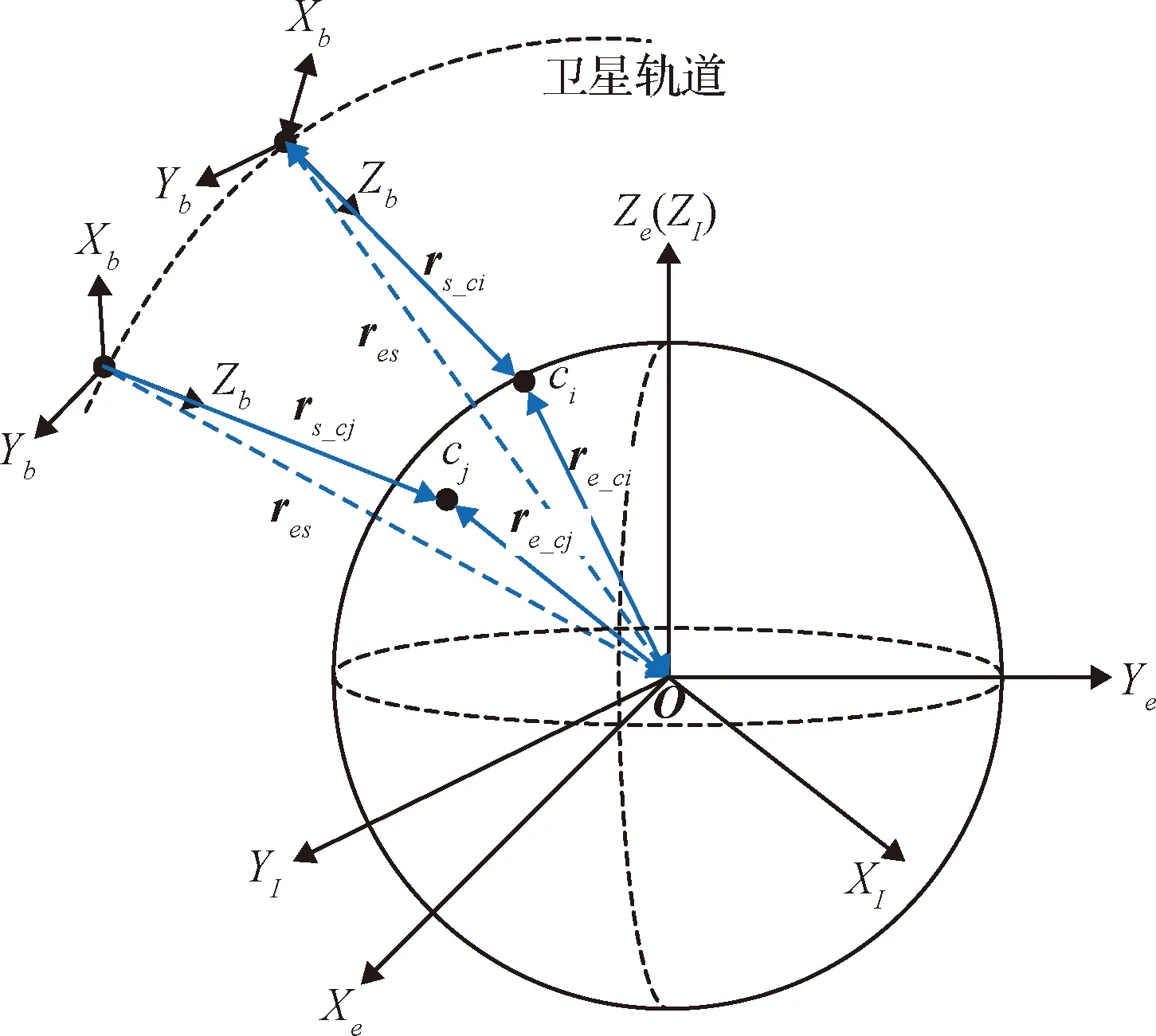
图1 卫星姿态机动示意图Fig.1 Sketch of satellite attitude maneuver
设t1时刻卫星和目标点cj的位置矢量分别为res和re_cj,则卫星指向目标cj的惯性矢量可表示为:
rs_cj=re_cj-res
(9)
为了将rs_cj变换到t0时刻的卫星本体坐标系下,考虑如下由四元数描述的方向余弦矩阵:
(10)
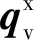
(11)
进而可得t0时刻rs_cj在本体坐标系下的投影:
(12)
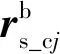
(13)
(14)
进一步,便可得到t1时刻的姿态四元数:
(15)
至此,可建立卫星对目标成像时刻与观测姿态的唯一关系,若给出一组目标观测状态和成像时刻的可行解,便可唯一确定卫星在整个观测过程中的姿态序列。通过调整和优化两决策变量可以改变序列之间的机动角度,进一步可以改变观测收益和目标间姿态机动的能耗。
2.2 能量最优姿态机动
由于在规划模型的指标函数中包含对姿态转移过程能量的优化,因此,需要在两观测目标间满足约束条件d)的情况下确定姿态机动能量最优解。
考虑如下卫星姿态运动学与动力学模型:
(16)
其中:ω=[ω1,ω2,ω3]T表示卫星惯性姿态角速度。I=diag(I1,I2,I3)代表三轴转动惯量。
指标函数:
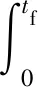
(17)
状态与输出约束:
(18)
式中:q0和qf分别代表卫星在上一目标点观测结束的期望姿态和下一目标点观测开始的期望姿态,tf表示卫星姿态从上一目标转移至下一目标点的转移时间。由于姿态运动方程具有强非线性,上述问题的求解需借助非线性优化算法。考虑非线性优化过程复杂,求解耗时较长,且受初值影响较大等问题,不适于求解本文描述的复杂规划问题的子问题。因此,本文尝试通过将模型线性化,结合传统最优控制的极小值原理进行求解。
考虑将卫星简化为一球体,其绕任意轴旋转的转动惯量均为常值,沿各轴的控制力矩也假定一致。实际任务中,为不失保守性,可令Ir=max{I1,I2,I3}。给定卫星初末姿态下的能量最优姿态机动为绕欧拉轴旋转的过程。基于以上分析,可得到简化后的卫星姿态动力学方程:
(19)
式中:θ,ω,ur分别为沿欧拉轴的角度、角速度和力矩,对应有如下能量最优姿态机动问题。
指标函数:
(20)
状态与输出约束:
ω(0)=0,ω(tf)=0
(21)
θ(0)=0,θ(tf)=θr
(22)
|ur|≤umax
(23)
其中:欧拉轴e=[ex,ey,ez]T,并且有|e|=1以及沿欧拉轴的转角可通过已知的初末姿态四元数唯一确定。沿欧拉轴的最大输出力矩umax
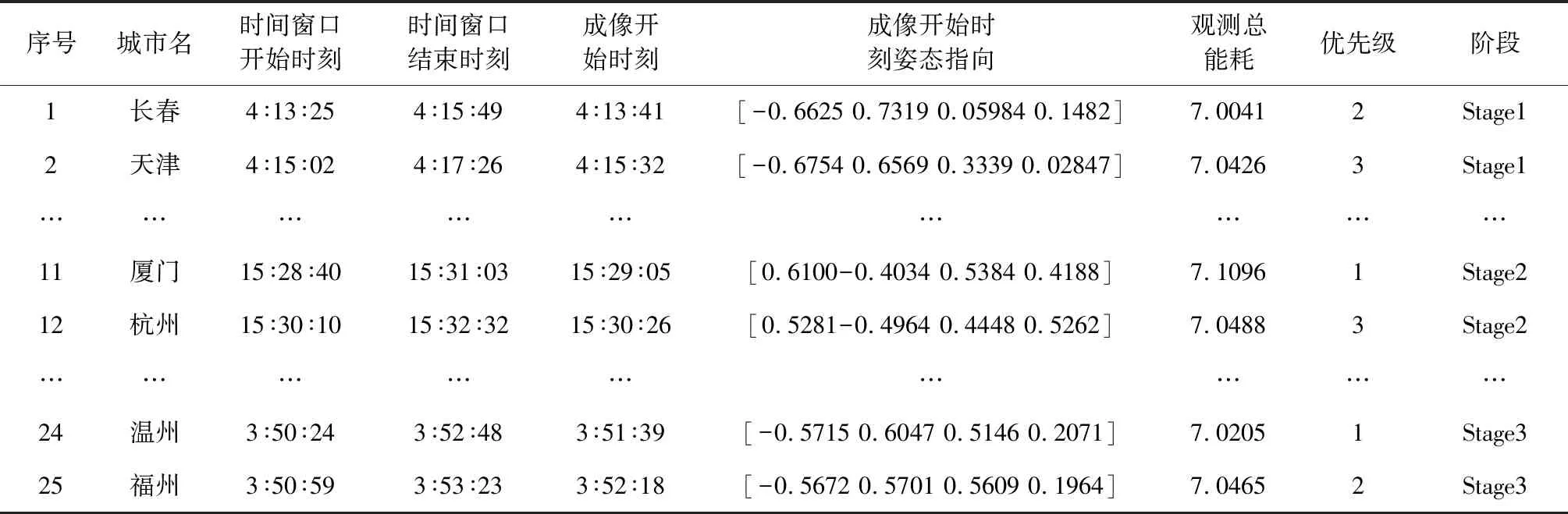
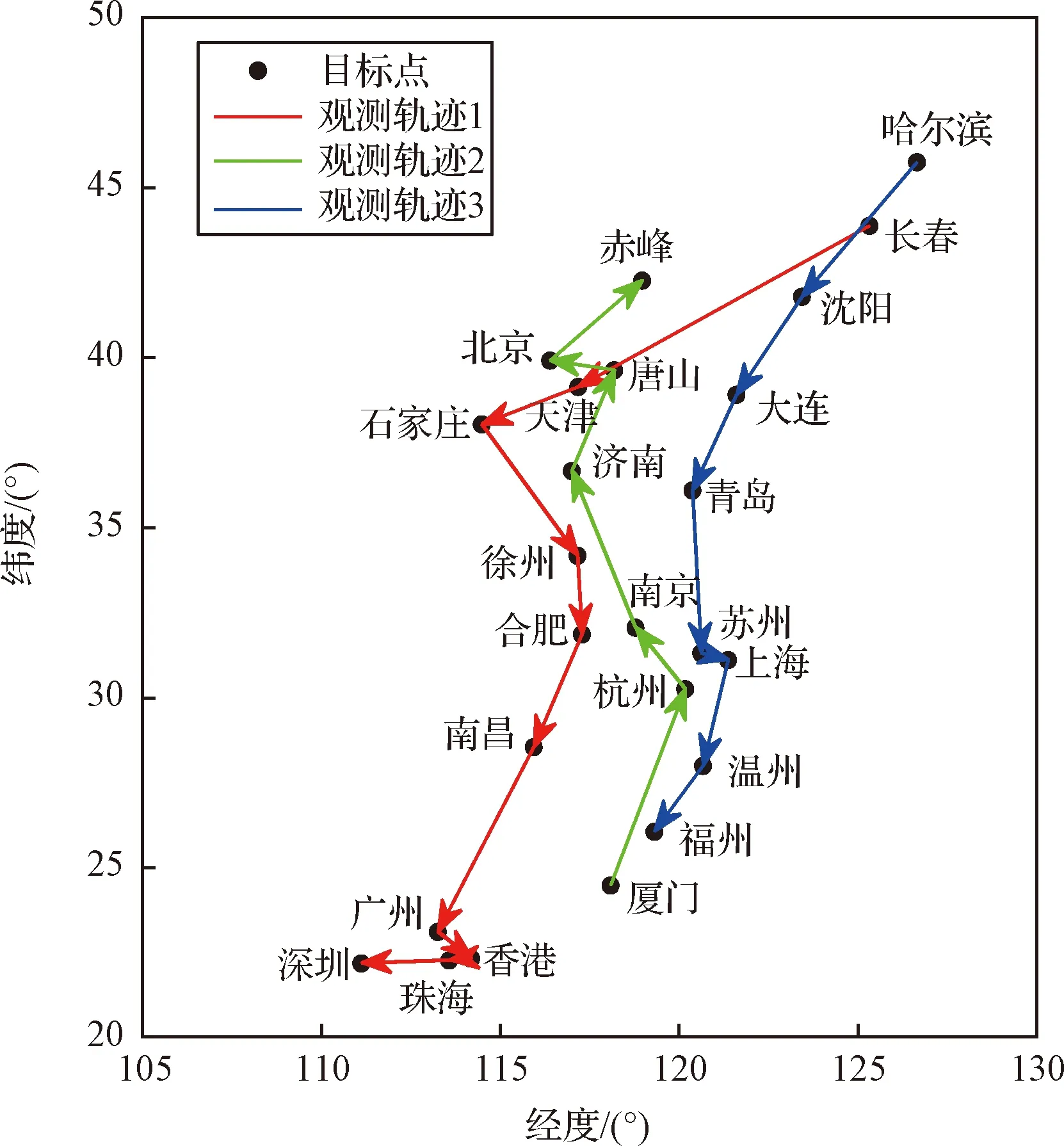
(24)
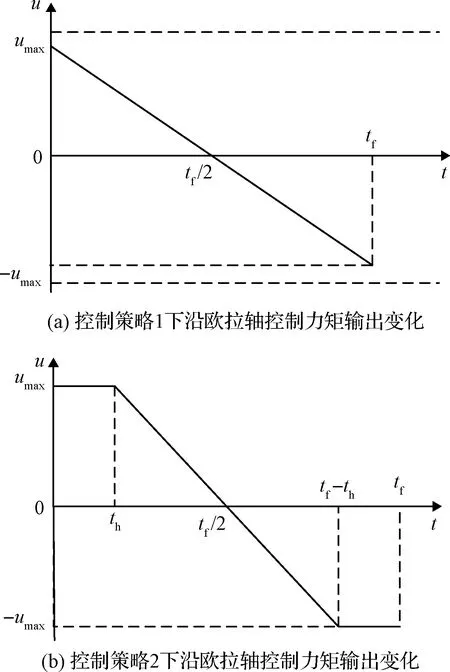
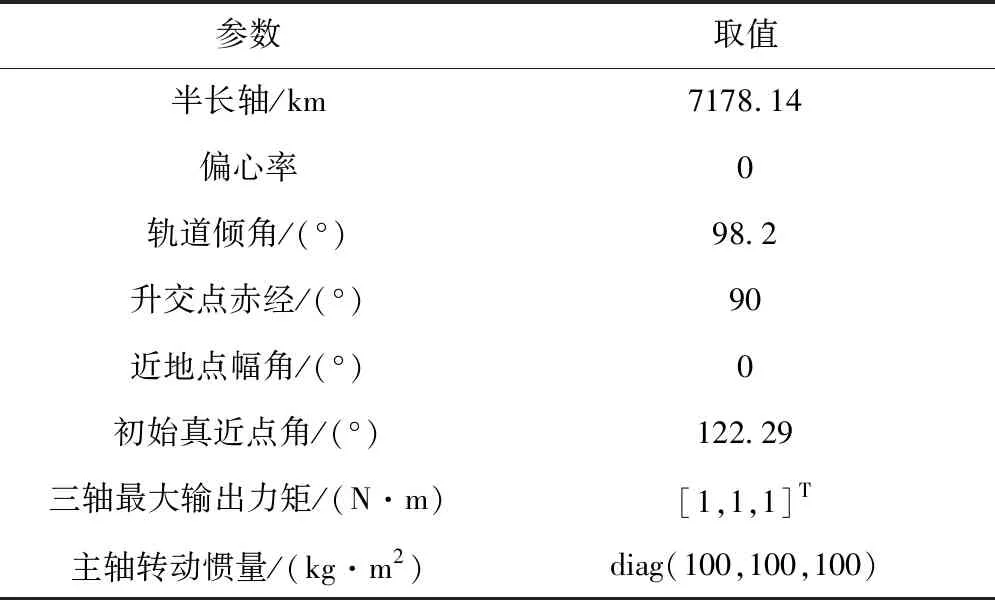
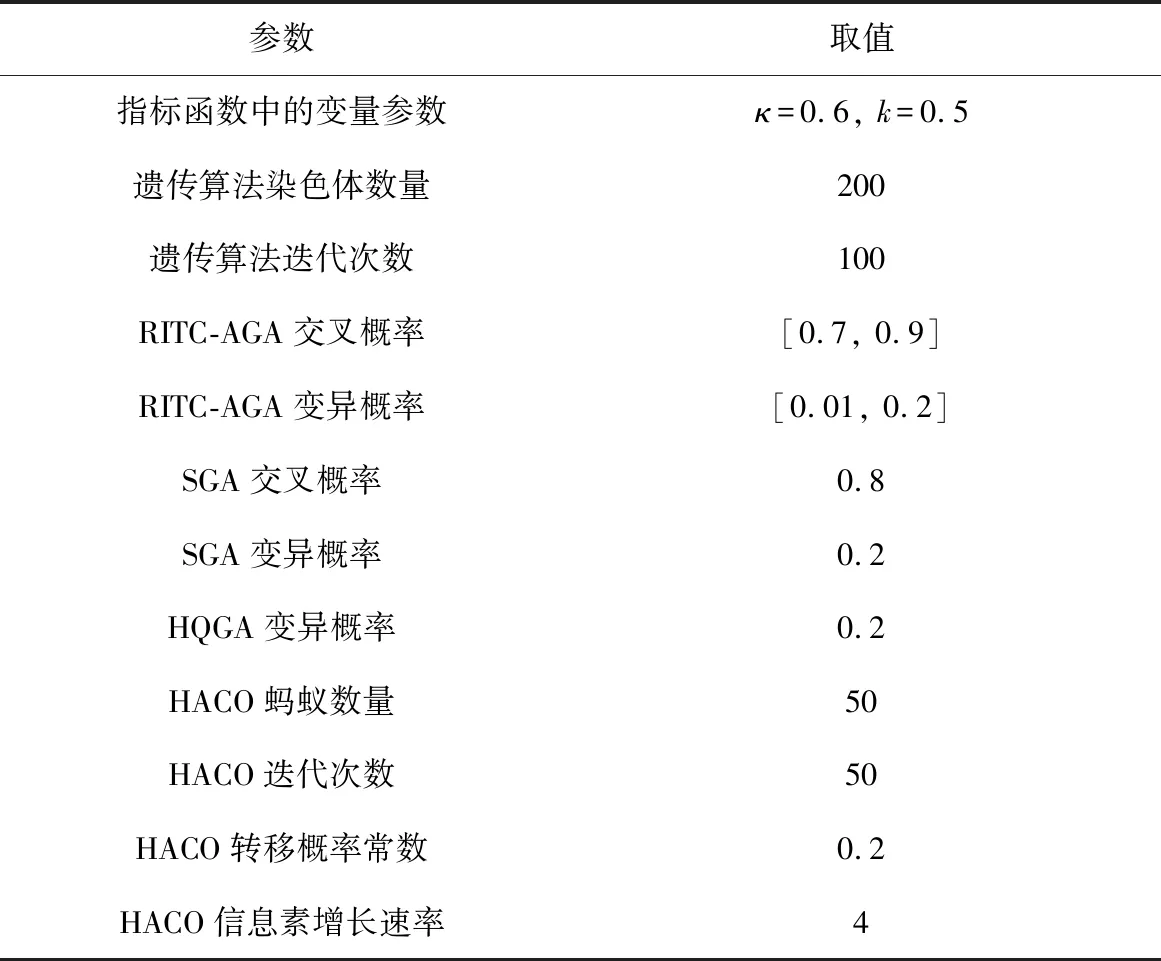
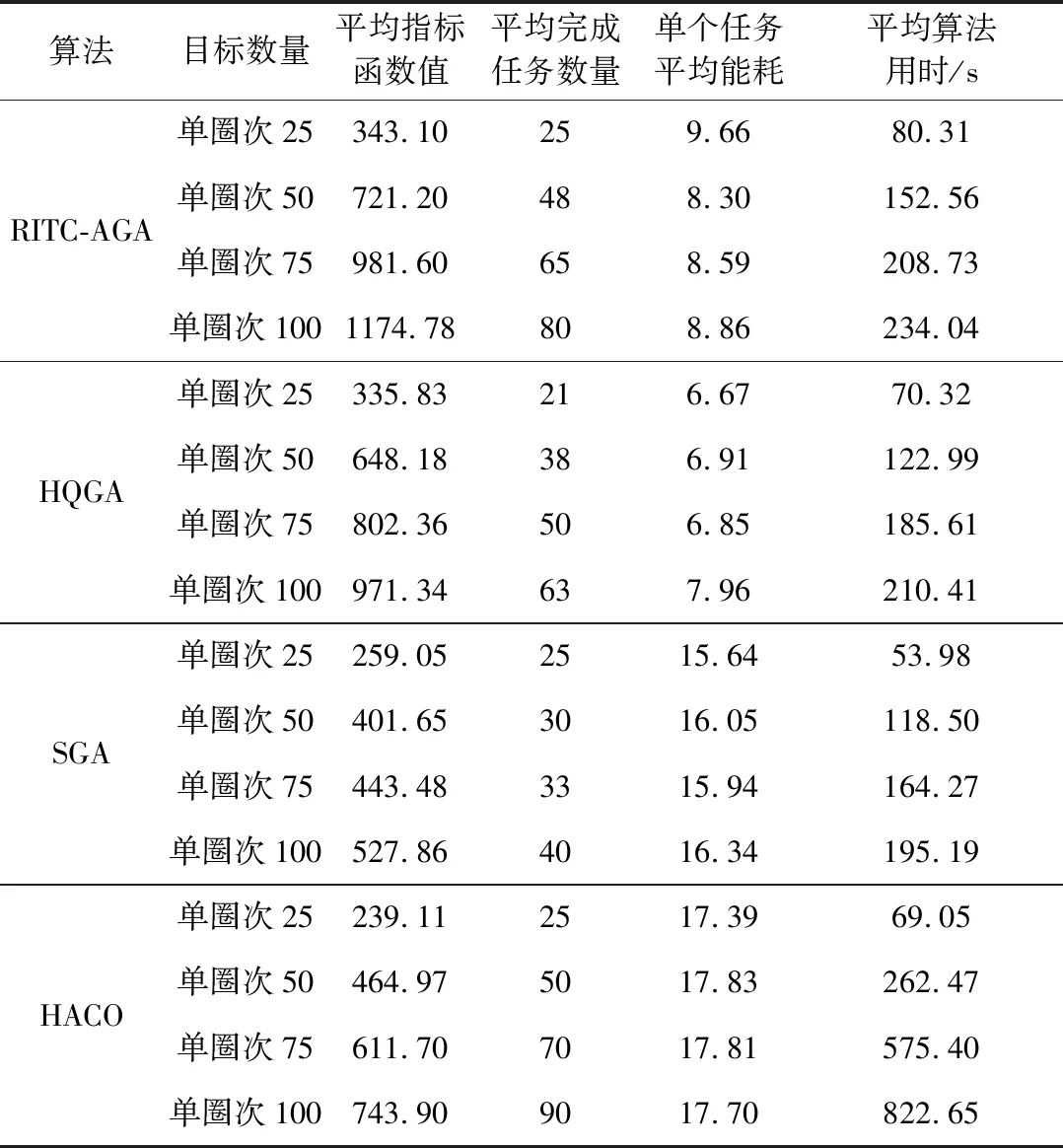
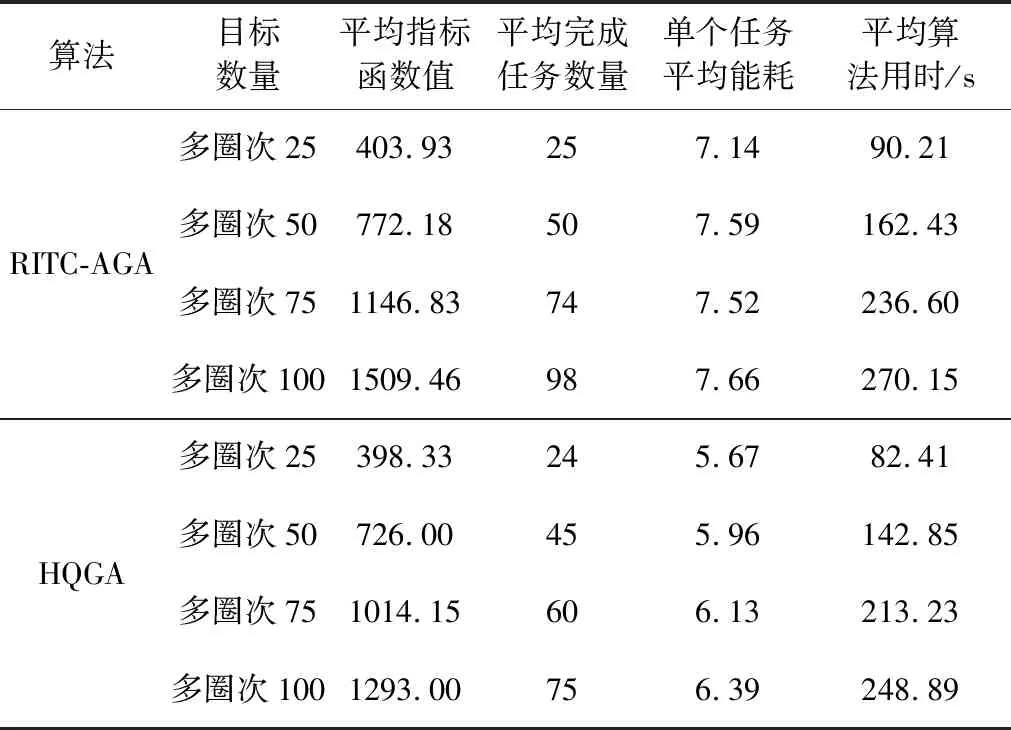
由最优控制理论可知,当初末状态下的角速度均为0时,单次姿态机动对应的tf必须为固定值,否则该能量最优控制问题无解。对于待观测的相邻两目标点ci,cj,假设姿态机动过程完全符合约束条件d),则有0 对于上文描述的最优控制问题,利用极小值原理可以得到能量最优控制 (25) 协态变量 (26) 其中策略1称为线性控制,策略2和3称为“饱和-线性-饱和”控制,两类控制策略中输出力矩随时间变化的示意图如图2所示。 图2 能量最优控制下沿欧拉轴控制力矩输出变化Fig.2 Energy optimal control torque along Euler axis 对于策略1,可得能量最优解为: (27) 其中:终端时刻tf需满足: (28) 以策略2为例,设两次控制切换时刻分别为th,tf-th,可得能量最优解为: (29) 其中: (30) 终端时刻tf需满足的边界条件为: (31) 进一步,当机动角度θr固定,th=tf/2时,有 (32) 此时,控制策略变为“饱和-饱和”控制,中间的线性控制段消失,此时的控制形式为终端时间任意的时间最优控制解,此时能耗为 (33) 根据以上分析,在卫星姿态机动开始时刻姿态与位置已知,目标位置已知,观测时刻固定的情况下,姿态机动角度θr固定,此时姿态机动g耗时存在下界 (34) 此时,约束条件c)被转化为不等式约束。 进一步,根据式(5)可知,在满足约束d)的情况下,允许的时间取值范围为: (35) 根据式(34)~(35),给出的可行解若要同时满足约束条件c)d),则应保证 (36) 其中:θr的求解过程在2.1节中叙述。 遗传算法中,将待求解问题的可行解从其解空间转换到遗传算法所能处理的搜索空间的转换方法称为编码。编码规则的设计对遗传算法的求解效率有至关重要的作用。解码过程与编码过程相对,即将染色体表示的搜索空间通过固定的规则转换为实际优化问题的决策变量,进而通过决策变量完成遗传算法中适应度函数的计算,便于整个遗传算法迭代流程的进行。 本文设计了一种基于相对开始成像时刻的实数编码方式。将每个目标点相对于其时间窗口的开始成像时刻作为基因,对于目标点个数为n的观测任务,可利用n个基因构成一个染色体。这样便保证了遗传算法在迭代过程中产生的可行解始终满足约束条件f)。解码过程基于每个基因点位对应目标点的时间窗口,得到其实际开始成像时刻,若目标点的开始观测时刻导致其观测时长不满足约束条件g),则代表其不进行观测。这样通过一维实数编码方式便可实现对目标观测状态和成像时刻两个决策变量的编码与优化求解。 目标点拥有多个时间窗口时,需要完成对时间窗口的选择,这时,对于每个目标点对应的基因点位,设定其取值范围为所有时间窗持续时间的总和。对于解码过程,首先将基因点位的取值按顺序减去目标时间窗口时长,当得到的结果为负时,此时对应的时间窗口即为目标点的开始成像时刻所在的时间窗口。 基于以上分析,可以得到编码过程的步骤: 2)对每个基因点位,在取值范围内生成随机数作为其初始值,将所有基因点位结合成为一个染色体(个体),此时对某一条染色体的编码完成。 3)反复执行步骤2),直到染色体数量等于设定的最大染色体数量,完成初始染色体的编码。 同样地,也可得到单条染色体解码的基本步骤: 1)对于目标点ci,对应基因点位取值为tri,令j=1,t=tri; 3)判断t的取值,若t≥0,则令循环变量j增1,并返回至步骤2);若t<0,则转到步骤4); 5)反复执行步骤1)~4)直到染色体中每个个体都得到绝对成像时刻; 7)依据得到的每个目标点的绝对开始成像时刻的早晚,对目标点进行排序,得到观测序列,完成解码。 表1给出了一组目标点可见时间窗口的示例数据,根据示例数据可以得到编码解码过程如图3所示,图中阴影的基因点位表示对应目标点不被观测。 表1 目标点时间窗口示例Table 1 Example of time windows of point targets 图3 编码与解码过程示意图Fig.3 Sketch of encoding and decoding process 相比于已有文献[13,14,17-21]中的编码方式,本文所述的编码方式有如下优势: 1)编码方式简单:不同于文献[13,19]中采用的二维编码方式,本文仅通过一维编码即可同时完成对两个决策变量从解空间到搜索空间的完整映射,显著降低了遗传算子设计时的复杂度。 2)迭代效率高:不易产生无效的可行解。对于时间窗口相邻且不存在重叠的目标点,其观测顺序必定是确定的。若采用现有的基于观测序列的符号编码方式,在进行迭代过程中会出现时间窗口靠后的目标点顺序位于时间窗口靠前的目标点,这样就造成了无效的可行解。对于基于相对成像时刻的编码方式便不存在这类问题,在遗传算法执行过程中,其对于观测序列的迭代优化只存在于相互重合的时间窗口对应的目标点之间,对于不重合的时间窗口,只进行成像时刻的优化。 3)适用于长规划周期,卫星多轨道圈次,目标多时间窗口的情况。目标点存在多个时间窗口时,首先需要完成对时间窗的选择,利用本文的编码方式,通过调整基因点位的取值便能完成时间窗口的选择。而基于观测序列的符号编码方式较难完成对时间窗口的选择。 3.2.1选择算子 选择算子采用精英保留策略和轮盘赌转法(Roulette wheel selection,RWS)。 精英保留策略是指保留每一代中染色体适应度函数值最大的,即适应度函数值最高的染色体一定会被选中,遗传至下一代。 对于其他染色体,则采用轮盘堵转法确定其是否被选中。首先计算该染色体在整个中群众被选中的概率和累计概率,表示为: (37) (38) 式中:Pi为第i个染色体被选中的概率;Qi为第1个染色体到第i个染色体的累计概率。N为种群中染色体数量。之后产生一个随机数r∈(0,1),其满足Qi-1 3.2.2自适应交叉算子 交叉算子采用部分映射交叉法(Partial-mapped crossover,PMC)。具体做法为,对于待交叉的两个个体,随机确定两个基因点位,将两个点位之间的基因进行调换,即完成交叉操作,如图4所示。对于种群中相邻的两个染色体,以交叉概率Pc进行交叉操作。Pc的大小基于染色体的适应度值在一定范围内自适应变化,由式(39)确定: (39) 其中,Pc1和Pc2分别代表交叉概率的上界和下界,在算法迭代开始时设定。为进行交叉的两个染色体中的较大的适应度值,Favg和Fmax分别代表种群中的平均适应度值和最大适应度值。式(39)表示对于种群中适应度较小的个体,采用较大的交叉概率,从而增加搜索效率,加快寻优进度。 3.2.3自适应变异算子 变异算子中,首先根据变异概率Pm确定染色体是否发生变异,对于发生变异的染色体,随机选取一个基因点位,然后生成该基因取值范围内随机数进行替代即可,如图5所示。 图5 变异过程Fig.5 Mutation process Pm同样基于染色体的适应度值在一定范围内自适应变化,由式(40)确定: (40) 其中:Pm1和Pm2分别代表交叉概率的上界和下界,在算法迭代开始时设定。式(40)表示,对于适应度较高的个体,采取较高的变异概率,防止其陷入局部最优,使得算法在迭代末期仍具有一定的寻优能力,而由于精英保留策略的存在,较高的变异概率不会破坏已有的最优个体。 通常情况下,遗传算法的优化目标是使适应度函数达到极小值,结合式(1)表征的指标函数,可定义适应度函数如下: (41) 设通过遗传算子迭代得到的染色体解码后得到的可行解对应的观测序列和观测时刻集分别为Q′,T′,根据3.1节可知,可行解Q′,T′满足约束条件(e)(f)(g),但不一定满足其他约束条件,需基于第2节所述的方法,以约束条件(a)(b)为以满足的条件,对约束条件(c)(d)进行检查。对于序列中相邻的两目标点ci,cj若两目标点间的姿态机动时间不满足约束条件(c)(d),则默认删除观测序列Q′中的后序任务,即目标点cj,及其在T′中对应的成像时刻tsj。通过对Q′的遍历完成约束检查,最后得到满足所有约束条件的观测序列与观测时刻Q,T进行适应度函数计算。 综上,可以得到RITC-AGA求解敏捷成像卫星任务规划问题的基本流程如图6所示: 图6 RITC-AGA流程图Fig.6 Flow chart of RITC-AGA 本节主要考虑卫星在较短的任务执行时段,对待观测目标点最多只有一个可见时间窗口下的可行性验证。仿真采用个人PC完成,CPU型号为Intel Core i5-8300H@2.3 GHz,内存为8 GB。 首先选取中国境内的25个城市作为待观测目标点,规定每个目标点固定观测时长为10 s,将目标分成1~3级优先级,划分结果见表2。卫星轨道为太阳同步轨道,卫星的具体参数由表3给出。仿真过程中RITC-AGA的各项参数见表4。仿真结果如图7、表5所示。 表5 对我国境内25个城市进行观测的任务规划结果(部分)Table 5 Task planning results of 25 cities in China (part) 图7 RITC-AGA得到的观测轨迹Fig.7 Observation trajectory obtained by RITC-AGA 表2 各目标点(城市)的优先级Table 2 Priority of each point target(city) 表3 卫星参数Table 3 Satellite parameters 为进一步测试本文算法的性能,继续设计了目标点数量分别为25、50、75、100,四组不同规模下的仿真实验,并与基于序列编码的遗传算法(SGA)、基于混杂编码的量子遗传算法[19](HQGA)、启发式蚁群算法[12](HACO)进行对比。其中,HQGA在处理姿态机动过程相关约束和姿态机动路径采用本文第2节叙述的方法,SGA和HACO采用文献[12]叙述的姿态约束检查与姿态机动路径确定方法。四种算法的参数设定由表4给出。仿真时间设定为24 Dec 2018 04∶00∶00——24 Dec 2018 04∶50∶00,目标点均匀分布在卫星在此段时间的星下点轨迹周围并保证卫星对每个目标都可见,目标点的优先级随机设定为1~3。卫星参数与上述实验相同,每组仿真场景运行50次,选取平均指标函数值、平均任务完成数量、单个任务平均能耗、算法平均运行时间作为评估指标。仿真对比结果见表6。 表4 算法参数Table 4 Algorithm parameters 由表6可知,在问题规模相同的情况下,RITC-AGA相比其他三种方法总能得到更高的收益,验证了本文所设计算法的优越性。进一步,对比三种不同编码方式的遗传算法可知,在种群数量和迭代次数相同的情况下,基于相对观测时刻编码的遗传算法在解决卫星任务规划问题时拥有较好的迭代效率,在完成任务数量和指标函数值上总是优于剩下两者。特别地,SGA在问题规模增加时,指标函数值并未明显增加,但任务完成率急剧下降,这是因为基于序列编码方式在迭代时会产生大量的无效序列,问题规模增加时,无效序列所占比例会大幅增加,降低搜索效率。而RITC-AGA则是直接在时间域上进行搜索,对于时间窗不重叠的目标,其观测的先后顺序固定,此时通过时间域的搜索优化机动能耗;对于时间窗口重合的目标,则是通过对观测时刻的调整而调整前后的观测顺序,因而极大的增加了搜索效率,能够得到更加优质的结果。 表6 单时间窗口下的4种算法优化结果对比Table 6 Comparison of optimization results of four algorithms under single time window scenarios 对比单个任务平均能耗可知,RITC-AGA与HQGA结果相近,明显优于SGA和HACO。这是因为,SGA和HACO中,上层算法仅针对观测序列进行优化,序列确定后,将观测时刻固定在每个目标点的最早可达时刻,并采用“最大加速-最大减速”的方式进行姿态机动,而本文则是通过线性化的姿态动力学方程和能量最优理论对姿态机动约束检查和能耗估计,同时RITC-AGA、HQGA均可对观测时刻进行进一步优化,因此,会得更低的机动能耗。 对比四种算法运行时间可知,SGA算法在各类场景中运行时间均为最短,但问题规模增加时,其解的质量急剧下降。HACO在问题规模较小时运行时间较短,但问题规模增加时,其运行时长也急剧增加,在星载计算机算力受限的环境下难以应用。RITC-AGA在求解质量和运行时间上达到了互相平衡,能较好地适用于实际工程。 相同规模的目标观测问题,若规划时长增加,卫星在规划时段内对目标通常有多个可见时间窗口,则决策变量的解空间也会有所增加。若算法有较强的寻优能力,得到规划结果应优于在单时间窗口下的规划结果。因此,本节将设置与4.1节中相同的任务场景,将任务时间进一步增加,以验证基于相对成像时刻编码的遗传算法在多时间窗口下的适用性。 保持卫星和算法参数不变,将仿真时长设为一天,此时卫星可以对某些目标有多个可见时间窗口。首先以4.1节中观测我国25个城市的仿真场景为例,进行遗传算法在卫星对目标有多个时间窗口情况下的仿真效验,结果如图8、表7所示。需要注意的是,卫星在仿真时段内会多次经过中国上空,相邻两次经过中国上空的时间间隔较大,因此,需要将连续进行的观测任务按照卫星过境的次数划分为不同的阶段执行,划分依据为前后两任务的时间间隔大于卫星运行的轨道周期,本算例中,观测任务被划分为3个阶段,见表7。 图8所示为RITC-AGA得到的观测轨迹,在任务执行时段内,卫星共有三次经过我国上空,目标点的时间窗口数量最多为三个,因此,整个规划结果被分为三个观测阶段完成。表7给出了部分任务规划结果,最终任务完成率为100%,指标函数值为422.7648。三个阶段中观测的目标点数量分别为10、7、8,各阶段内的观测任务数量基本均衡。与图7中卫星对目标只有一个时间窗口的情况相比,任务完成率提高了16%,指标函数收益增加了14%,充分说明了算法在目标具有多时间窗口下的有效性。 表7 目标点有多时间窗口情况下的任务规划结果(部分)Table 7 Task planning results with multiple time windows for point targets (part) 图8 目标点有多时间窗口时RITC-AGA得到的观测轨迹Fig.8 Observation trajectory obtained by RITC-AGA when the point targets have multiple time windows 为衡量在不同问题规模下的算法性能,同样设计了与4.1节中4类问题规模一致的测试场景,并将仿真时长均设定为1天,其他参数保持不变。由于SGA和HACO不具备在目标有多时间窗口下的优化能力,因此只进行RITC-AGA与HQGA的对比实验,最后得到的实验结果见表8。 由表8可知,任务规模相同时,RITC-AGA在指标函数值和任务完成率上均好于HQGA,与在单时间窗口下的仿真结果一致。虽然HQGA具备对目标观测状态和观测时刻两个变量的求解能力,但由于其采用混杂编码方式,将两决策变量进行独立编码,独立迭代优化,并未考虑两变量之间的相互依存和耦合性,因此在迭代结果的最优性上略差于RITC-AGA。以上对比实验结果进一步说明了本文设计的基于遗传算法的求解算法在长规划周期,多时间窗口下的有效性。 表8 多时间窗口场景下两算法优化结果对比Table 8 Comparison of optimization results of the two algorithms under multiple time windows scenarios 本文针对敏捷成像卫星对多点目标连续观测的任务规划问题,将观测收益和姿态能耗两个指标作为优化指标,将目标点观测状态和成像时刻作为决策变量。将卫星在目标姿态机动的能量最优问题看作一个最优控制问题,并基于线性化的姿态动力学模型完成能量最优求解和姿态机动约束检查。设计了基于相对成像时刻编码的自适应遗传算法完成规划问题的求解,基于该编码方式可同时完成对观测序列和成像时刻两个决策变量的求解优化,且适用于长时间,多时间窗口的规划问题。最后分别在单一时间窗口和多时间窗口下的不同规模的仿真对比实验验证了算法的优越性和有效性。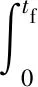
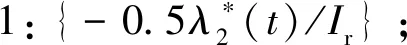
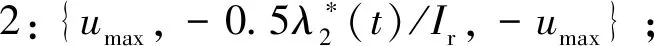
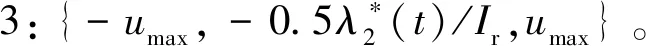
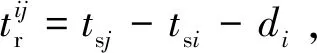
3 基于相对成像时刻编码的自适应遗传算法
3.1 编码与解码规则设计
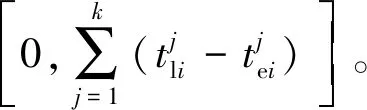
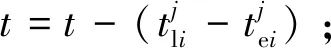
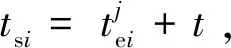
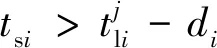
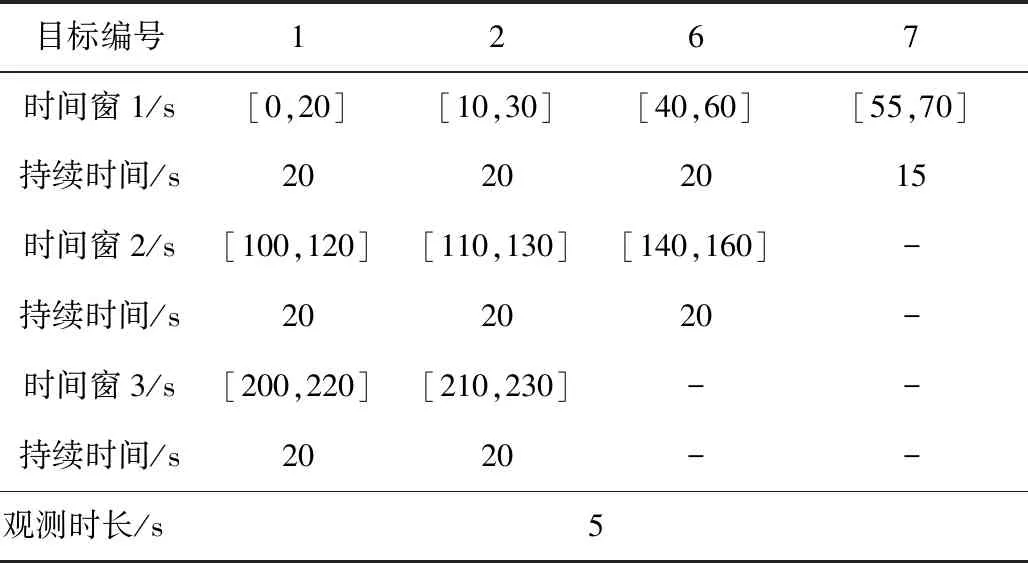
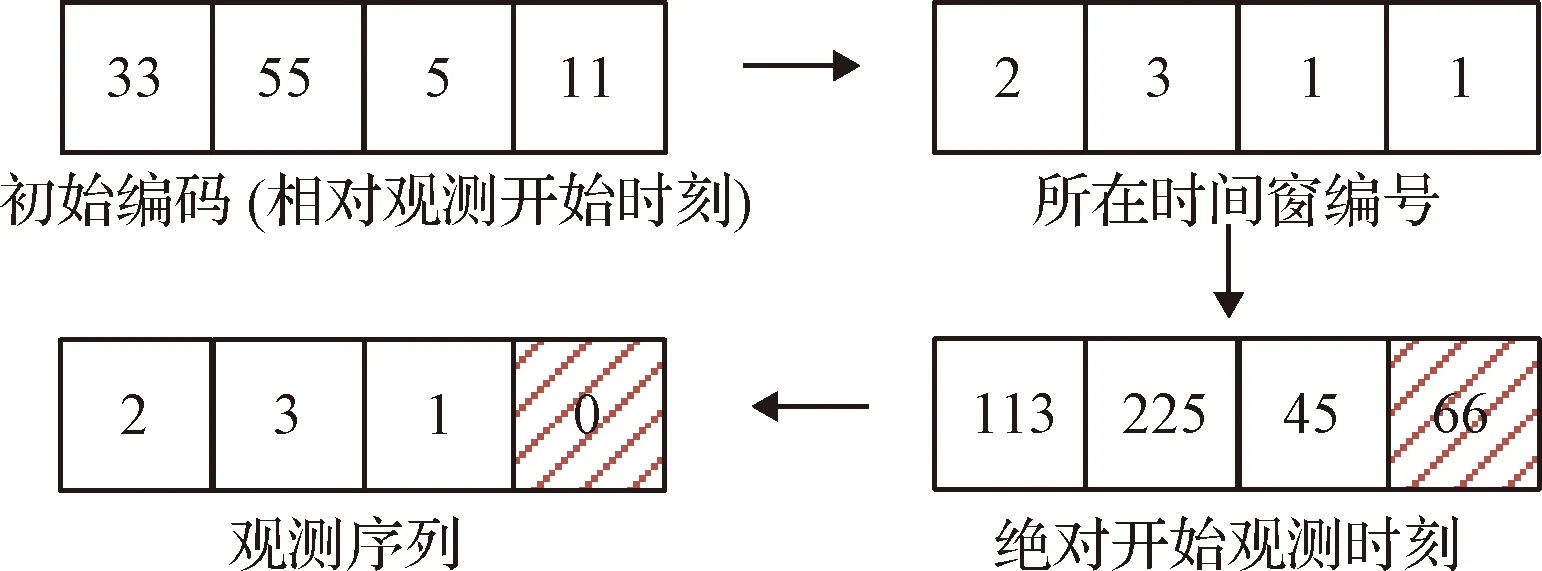
3.2 遗传算子设计

3.3 适应度函数计算
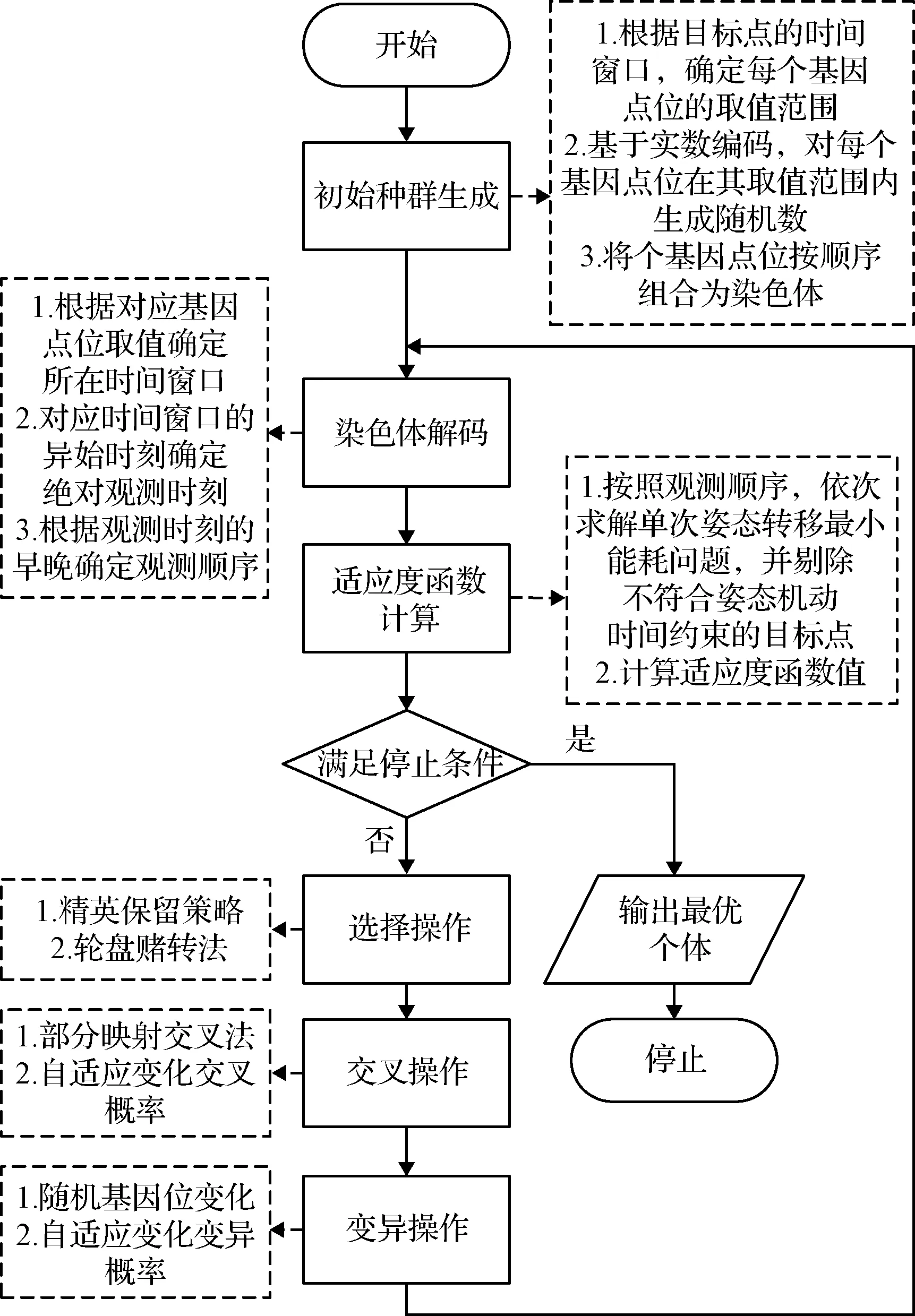
4 任务规划典型算例
4.1 单一时间窗口下的任务规划
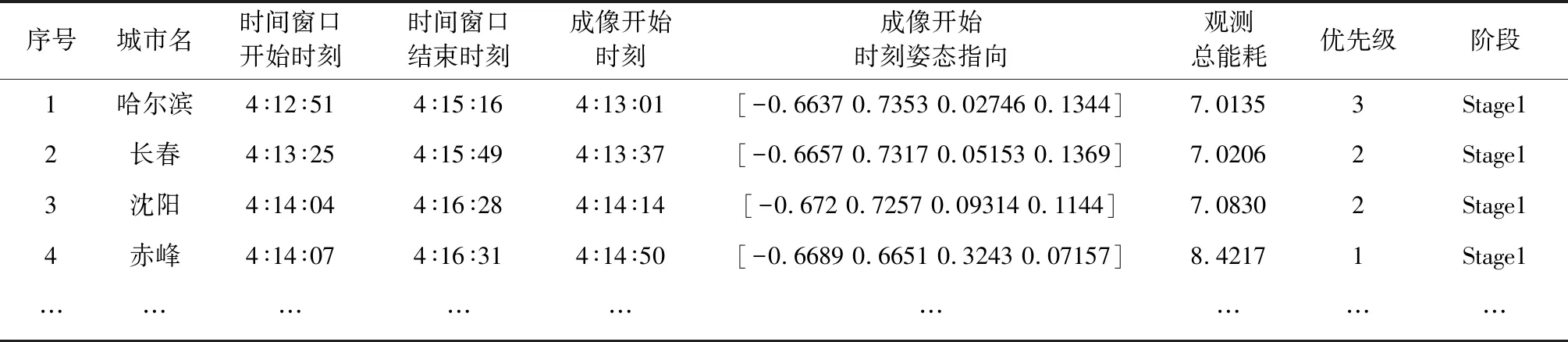
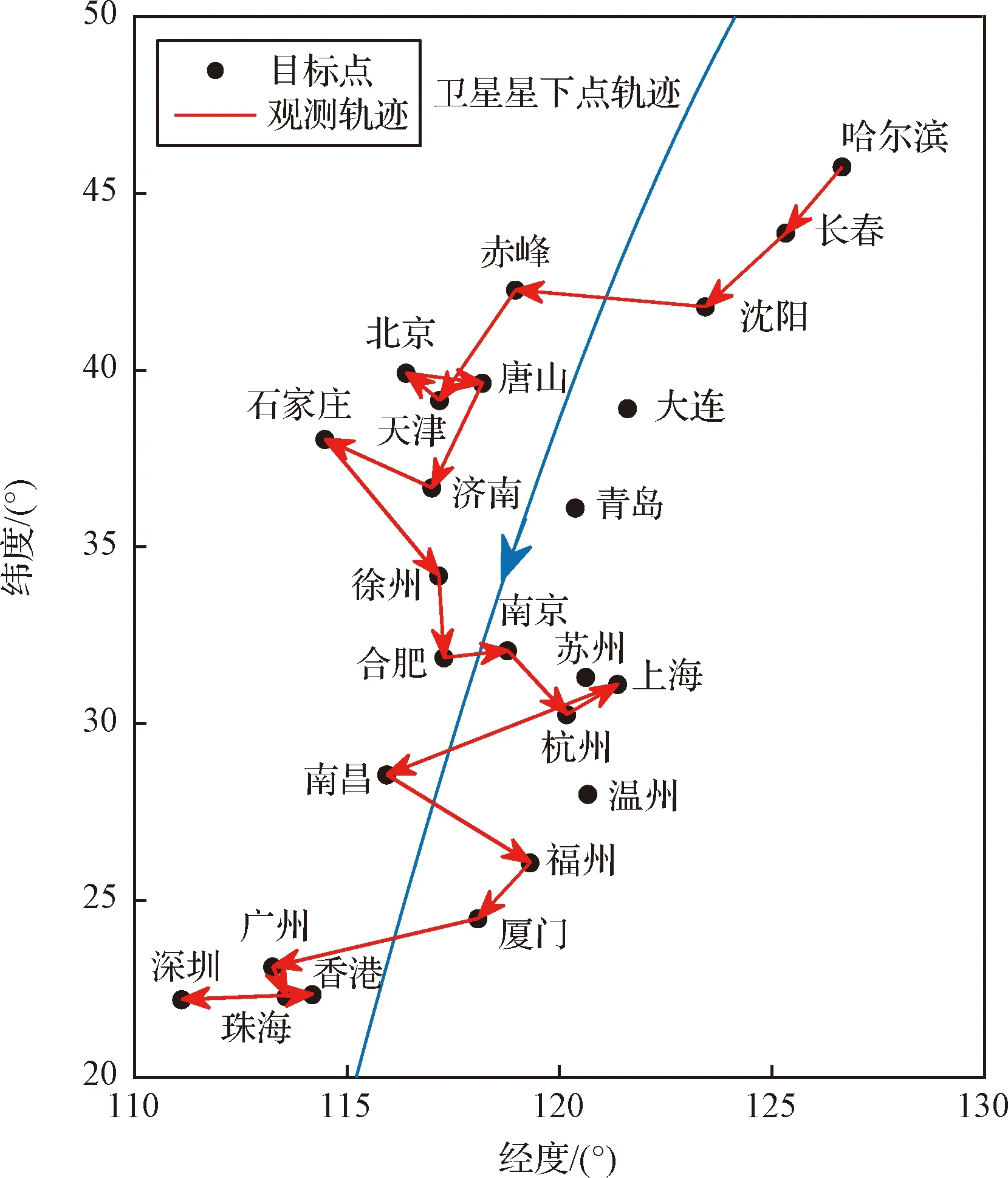

4.2 多时间窗口下的任务规划
5 结 论

