基于ANSYS抽油泵筒-柱塞摩擦副磨损规律分析*

谢文献 苏庆欣 郭立谦 孙 喆 张立军 郭伟健 张 辛

(1.中石化胜利油田分公司胜利采油厂 2.中国石油大学(华东)机电工程学院)

0 引 言

有杆抽油技术因简单方便、适应性强和使用指标良好在国内外油田得到广泛应用[1]。目前国内机械采油井中，有杆泵油井数占总生产井数的80%以上[2]。目前，抽油泵的主要问题是使用寿命较短，影响抽油泵使用寿命的关键因素是泵筒-柱塞摩擦副的磨损[3]。据不完全统计，抽油泵失效问题中70%是因为泵筒-柱塞摩擦副的磨损失效[4]。其中，除产出液的腐蚀性及液体中的砂粒作用之外，泵筒-柱塞的结构工艺参数，如涂覆层性能、抽油杆冲程及配合间隙等都对摩擦副性能造成较大影响，长时间工作会导致泵筒-柱塞摩擦副磨损严重，使泵失效的事故频繁发生。

国内外学者针对抽油泵泵筒-柱塞摩擦副的磨损机理及影响因素进行了相关研究。1998年,白理明等[5]对失效柱塞进行了金相分析和表面形貌分析，探讨了柱塞的失效机理。1999年，刘旭林等[6]在分析抽油泵柱塞失效特征的基础上，推断岀拉伤失效是砂粒在柱塞端部锥面和泵筒内表面之间产生自锁所致，通过试验研究证实了推断的正确性。2002年，娄晖等[7]对摩擦副材料选配进行了试验研究，在综合考虑成本、耐磨性和实际应用条件下，建议选用碳钢镍磷镀/碳钢镀铬作为抽油泵的泵筒/柱塞副配对材料。2004年，王旱祥等[8]用SEM法证实了镍磷镀泵筒与镀铬或喷焊柱塞摩擦副的可行性。2005年，胡桢[9]对有杆抽油泵的失效形式进行了分析，认为抽油泵失效的原因主要为：①失效零件结构不合理；②零件的耐蚀性能差; ③零件的热处理工艺不合理；④井液的矿化度高。2007年，卜凡俭[10]对抽油泵磨损机理进行分析，指明砂粒磨损是抽油泵失效的主要原因。

上述文献主要研究了抽油泵的失效机理，缺少在模拟工况下对抽油泵摩擦副进行优化分析。因此，本文主要研究抽油泵泵筒-柱塞摩擦副在模拟工况下的磨损状态，建立泵筒-柱塞模型，定性、定量地分析影响摩擦副磨损状态的工艺、结构因素和环境因素；设计正交试验研究摩擦副在不同配合间隙下，不同因素水平对其磨损状态的影响程度，并通过综合平衡极差分析法，确定在模拟工况下影响抽油泵摩擦副磨损状态的主要因素水平，确定摩擦副磨损最优的因素水平组合。研究结果可以为抽油泵结构、工艺参数及工作环境的合理选用提供指导，不仅可以减少打捞和更换抽油泵的工作，降低设备投资和维修作业费用，而且还能减少原油开采的停产次数，降低开采成本，对于提高油田的经济效益具有重要现实意义。

1 摩擦副仿真元建立及正交试验设计

1.1 假设条件

本文利用仿真方法分析抽油泵摩擦副的磨损状态。考虑计算方便性，做出如下假设：

(1)抽油泵泵筒-柱塞摩擦副在工作中受到轴向载荷和径向载荷，鉴于本模型研究在径向偏心下摩擦副的磨损状态，故只考虑径向液体压力；

(2)本模型考虑液体润滑，利用摩擦磨损实验仪确定液体在润滑工况下摩擦因数为0.110～0.158范围作为仿真输入数据。不考虑磨粒磨损和冲蚀磨损；

(3)泵筒和柱塞与其涂覆层为一个整体，仅两涂覆层间进行相对运动，分析涂覆层的磨损情况。

1.2 模型建立

抽油泵实际结构复杂，本文仅研究不同结构、环境和工艺参数对泵筒和柱塞摩擦副磨损的影响。柱塞冲次为6 min-1，不考虑阀的工作状态，泵筒和柱塞的模型依据API SPEC 11AX标准建立。本仿真模型泵筒采用B13厚壁泵筒，柱塞选用P23内螺纹柱塞。模型三维图如图1所示。其中：泵径95 mm，泵筒长度2 438 mm，壁厚8 mm；柱塞外径95 mm，柱塞长度1 200 mm。对于泵筒-柱塞的配合间隙，结合相关资料和企业所提供参数，配合间隙选取二级间隙，间隙为0.050～0.113 mm。

1—泵筒；2—泵筒镀层；3—柱塞焊层；4—柱塞。

1.3 网格划分

在网格划分中，需要充分考虑模型的结构特征。该模型在网格划分时，如果按照通常的自动控制网格划分方法，只能够划分为四面体网格，这是因为该模型存在许多不可选取的最小过渡界面，这些界面限制了自动控制网格和扫掠划分。若直接利用扫掠或强制六面体网格划分方法，会产生网格紊乱现象。因此，笔者采用多区域网格划分法进行轴承-棒料的网格划分。将泵筒-柱塞进行整体剖分，减少最小过渡面的数量，可以保障在结果准确的条件下提高收敛速度。网格划分模型如图2所示。

图2 摩擦副自适应网格划分模型

1.4 模型性能参数和边界条件

泵筒-柱塞摩擦副使用寿命在很大程度上取决于材料的力学性能和表面硬化质量。我国目前生产的泵筒表面硬化方法主要是渗硼和镀铬等工艺[11]。这些涂覆层既可以使结构表面光滑平整，也可以提升材料的耐磨性，对于复杂环境(腐蚀、含颗粒时)具有很好的保护作用。本模型采用泵筒镀铬和柱塞喷焊Ni60工艺，其性能参数如表1所示。表1中，ρ为材料密度；E为材料弹性模量；υ为泊松比；σs为材料屈服强度；H为材料硬度。

表1 泵筒柱塞涂覆层材料参数

本模型模拟运动工况为：泵筒及涂覆层保持固定，柱塞往复运动冲次6 min-1，两涂覆层之间存在摩擦接触，接触方式为非对称接触防止渗透[12]；确定泵筒和柱塞间的液体压力为9.9～17.9 MPa[13]。考虑到不同冲程对摩擦副的磨损程度会有较大影响，将抽油杆的冲程作为影响磨损状态的因素之一进行仿真分析。初步确定抽油杆冲程为150～500 mm，运动方式为余弦规律往复运动。

1.5 泵筒-柱塞摩擦副正交试验设计

正交试验设计以“正交表”为工具，表中的元素具有均匀分散性和随机性，因此可以用尽可能少的试验获得典型数据，得到多因素综合作用下的最优组合。根据前文分析的摩擦副的影响因素要求，本模型确定液体润滑摩擦因数、抽油杆冲程、泵筒液体压力及涂覆层硬度为影响因素，每个因素选取3个水平，建立4因素3水平的因素水平表，如表2所示。试验选用L9(34)正交表，确定的试验方案如表3所示。由表3可以看出，只需要9 次试验便可大体上反映34次试验的结果。

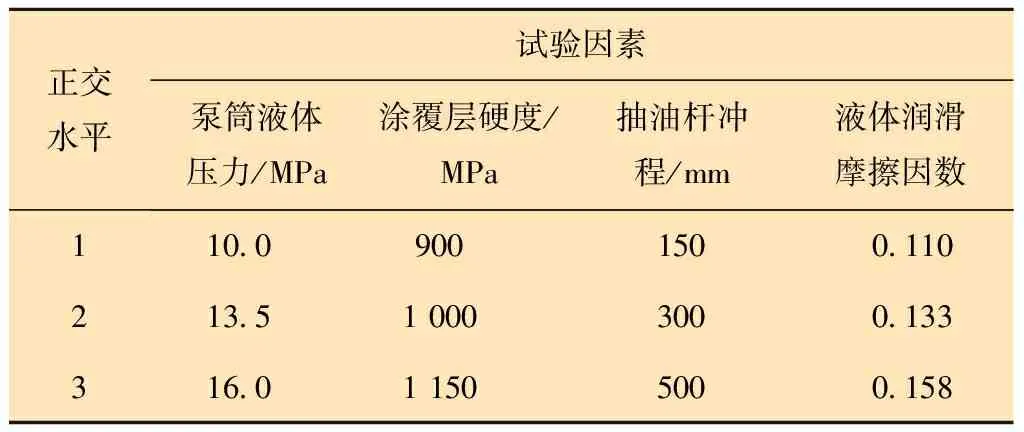
表2 摩擦副影响因素水平

表3 摩擦副L9(34)正交试验因素水平

2 间隙对摩擦副磨损的影响分析

2.1 配合间隙0.08 mm的仿真结果

对间隙0.08 mm的9组正交模型进行有限元仿真，分析结果如表4所示。从表4可见，配合间隙值为0.08 mm时，7号泵筒-柱塞摩擦副摩擦应力云图如图3所示。不同正交试验组摩擦应力曲线如图4所示。由图3和图4可知，在恒定液体压力作用下，由于考虑变形条件，泵筒和柱塞涂覆层的接触状态由刚开始的线接触逐渐变成一段范围内的曲面接触，且7号模型接触面的滑动摩擦应力变化范围为7.902 8～54.345 0 MPa，3个模型的应力变化规律均随着液体压力的变化近似成余弦函数变化，符合对应输入工况。观察60 s时泵筒涂覆层处的滑动摩擦应力，最大值出现在泵筒镀层与柱塞焊层接触的分割线上，并在左右半面内按一定程度均匀分布有摩擦应力梯度，与预期的结果大致符合。但观察图4可知：间隙为0.08 mm时，1号和9号模型的摩擦应力分布均匀且稳定，无应力突变现象；而在25 s左右，7号模型泵筒-柱塞摩擦副的摩擦应力发生了突变，且摩擦应力变动范围较大。由泵筒磨损体积曲线(见图5)可知，正交试验模型摩擦副60 s内的磨损体积变化范围为0.204 72～0.418 51 mm3。其中，7号模型60 s内泵筒涂覆层的磨损体积最大为0.418 51 mm3，1号模型60 s内磨损体积最小为0.204 72 mm3。3个模型磨损体积随着时间的延长线性拟合效果较差，存在磨损状态不均匀的现象，初步判断是输入参数对磨损状态产生了影响。但对9组正交试验模型进行仿真后发现，间隙值为0.08 mm时，9组正交模型的摩擦应力曲线和磨损体积曲线均出现了不同程度的波动，线性拟合效果欠佳，因此考虑选取不同间隙进行正交试验进行对比分析。

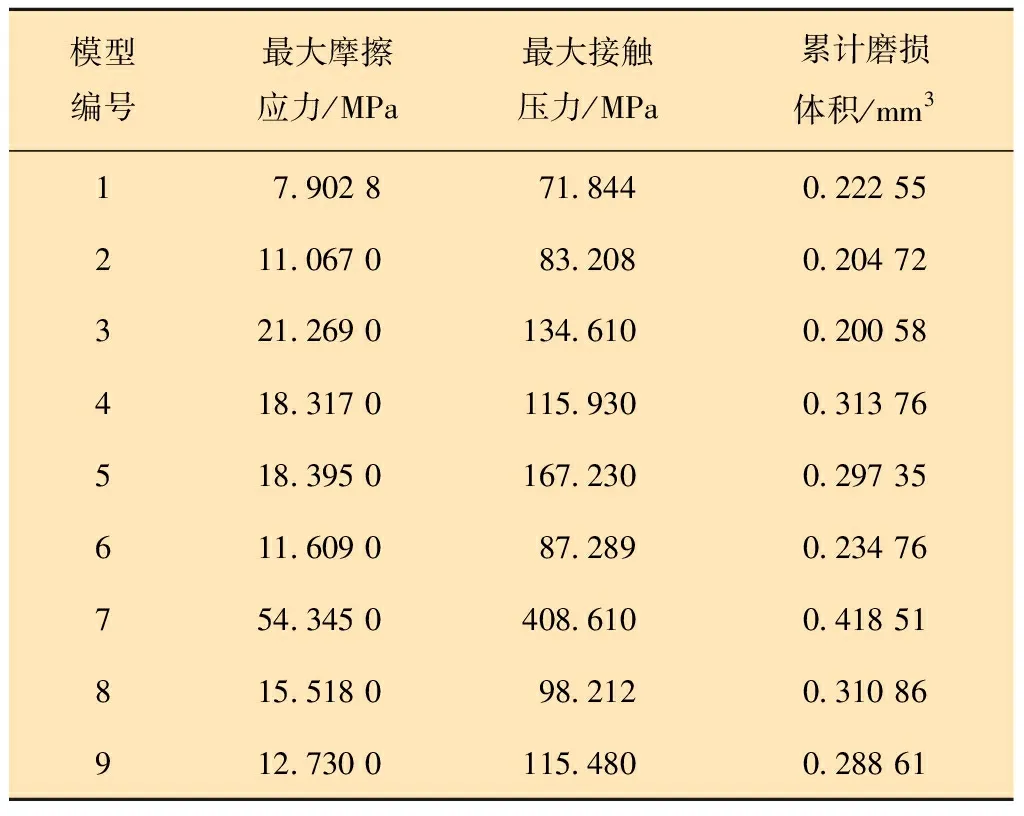
表4 配合间隙为0.08 mm时摩擦副仿真结果

图3 7号模型摩擦应力云图(间隙为0.08 mm)

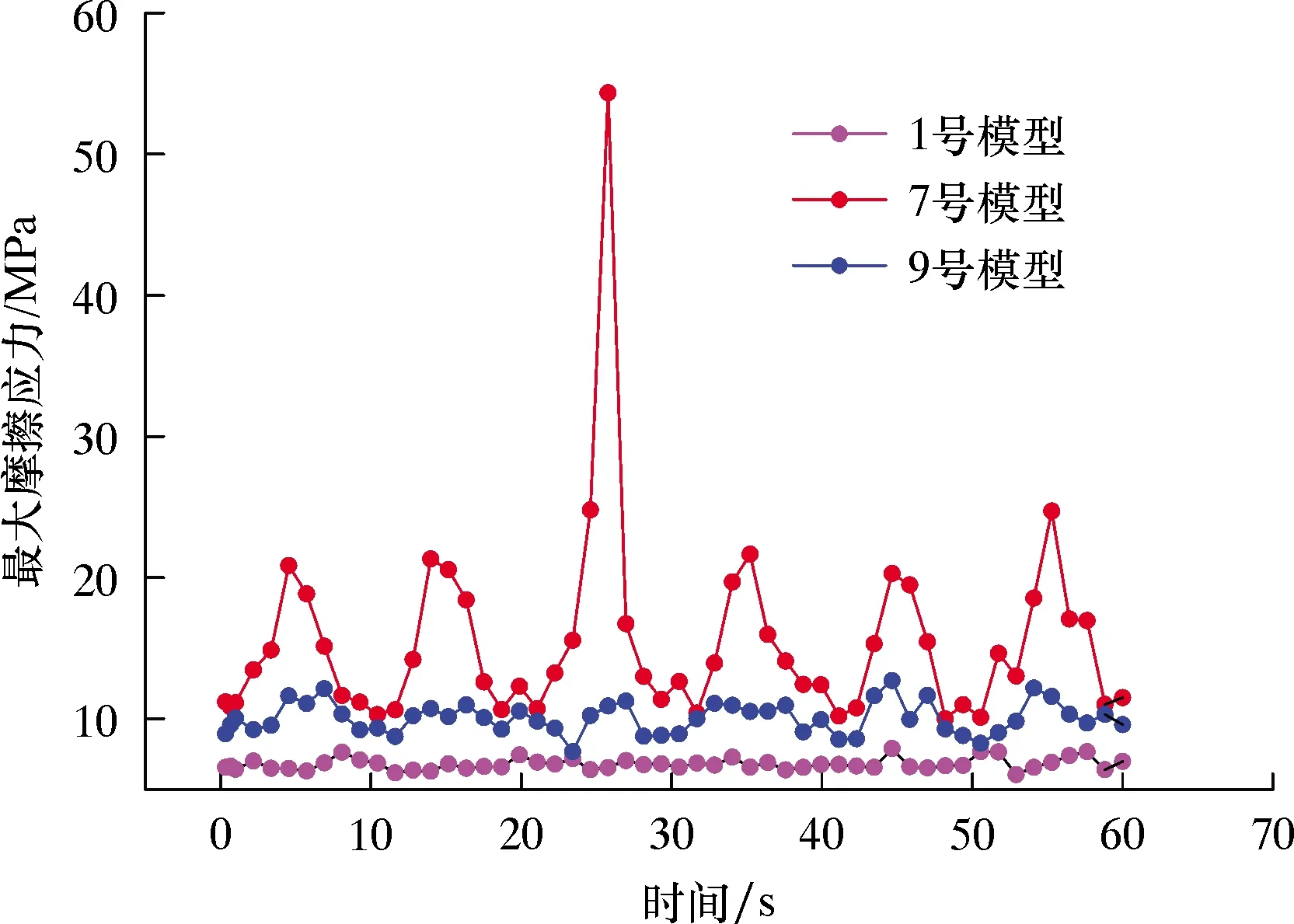
图4 不同模型摩擦应力曲线(间隙为0.08 mm)

图5 不同模型磨损体积曲线(间隙为0.08 mm)

2.2 配合间隙0.05 mm的仿真结果

考虑到间隙为0.08 mm时摩擦应力和磨损体积的线性拟合效果不好，改变配合间隙为0.05 mm后，不同正交试验模型的仿真结果、7号模型摩擦应力云图、不同模型摩擦应力曲线及不同模型磨损体积曲线分别如表5、图6、图7及图8所示。由图6可知，在恒定液体压力作用下，由于考虑变形条件，泵筒和柱塞涂覆层的接触状态由刚开始的线接触逐渐变成一段范围内的曲面接触，且60 s时泵筒涂覆层处的滑动摩擦应力最大值出现在泵筒镀层与柱塞焊层接触的分割线上，并在左、右半面内按一定程度均匀分布有摩擦应力梯度，与预期的结果大致符合，与间隙值为0.08 mm的接触状态相同，但最大摩擦应力值略有减小。由图7和表5可知，3组正交模型摩擦副最大摩擦应力变化范围为6.945 7～14.106 0 MPa，且3个模型的应力变化规律均随着液体压力的变化近似成余弦函数变化，符合对应输入工况。与间隙值为0.08 mm的结果相比，间隙为0.05 mm时，不同正交模型的摩擦应力曲线分布均匀，在一定范围内稳定呈近似周期变化，且无摩擦应力突变现象。

表5 配合间隙为0.05 mm时摩擦副仿真结果

图6 7号模型摩擦应力云图(间隙为0.05 mm)

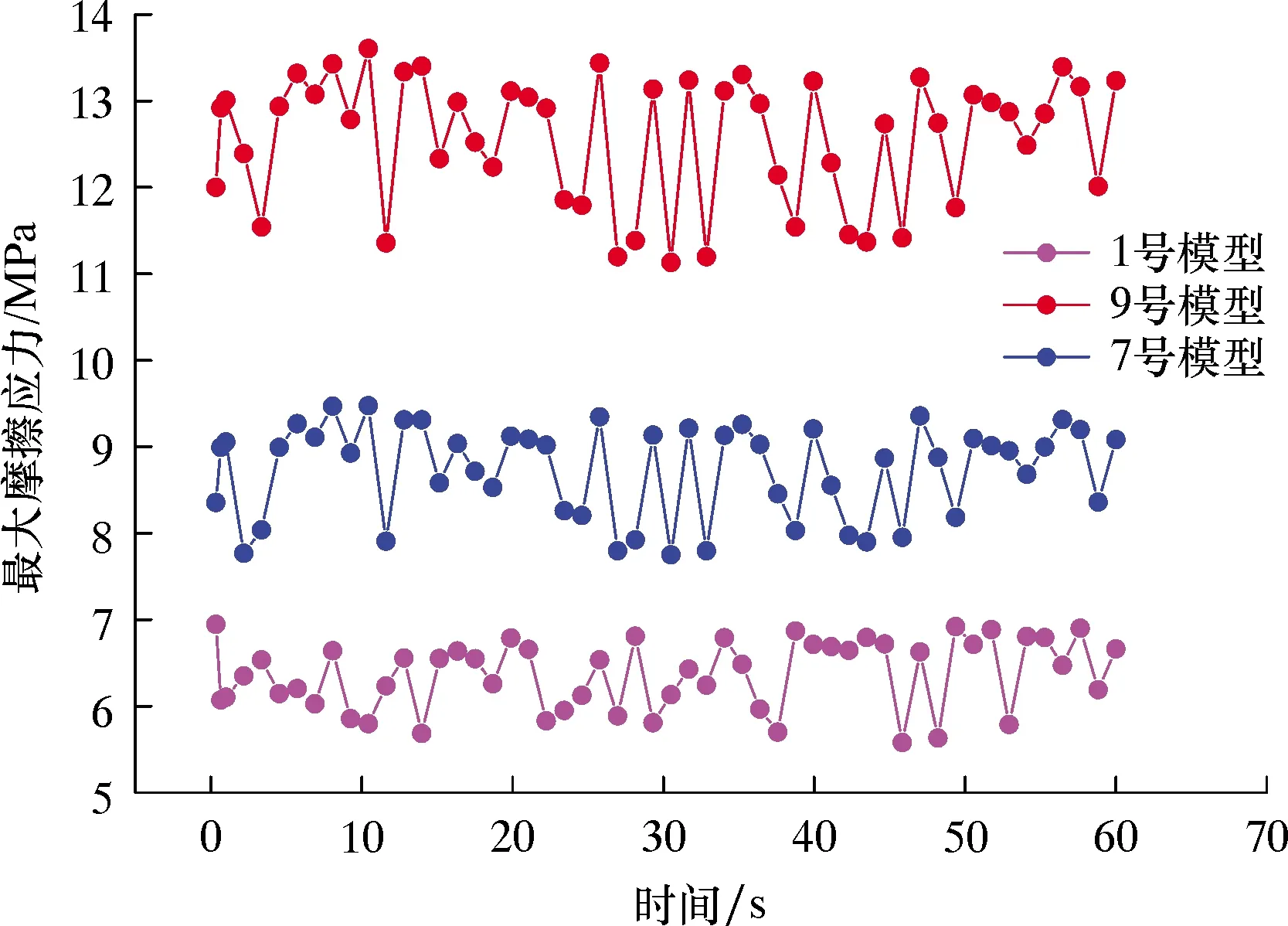
图7 不同模型摩擦应力曲线(间隙为0.05 mm)

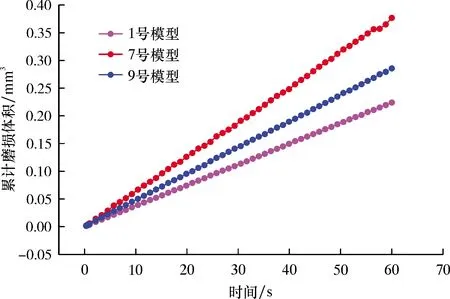
图8 不同模型磨损体积曲线(间隙为0.05 mm)

由图8可知，间隙值为0.05 mm时正交试验模型摩擦副60 s内的磨损体积变化范围为0.184 13～0.376 83 mm3。其中，7号模型60 s内泵筒涂覆层的磨损体积最大为0.376 83 mm3，而60 s内磨损体积最小的模型为3号，其值为0.184 13 mm3，磨损体积整体减小了10.05%。

上述分析说明，改变柱塞-泵筒的配合间隙会很大程度影响摩擦副的磨损状态，进而影响摩擦副的摩擦应力和磨损量。当间隙值为0.05 mm时，3个模型磨损体积曲线随着时间的延长基本呈线性增长，这是因为本仿真利用Archard模型，并设定法向载荷(液体压力)、相对滑行距离、磨损系数和材料硬度均为常数，所以磨损状态应呈均匀线性分布，符合理论模型工况，与间隙为0.08 mm相比，磨损状态均匀且线性拟合效果较好。

3 不同因素影响的正交试验分析

进行正交试验分析需要选取评价目标，对于泵筒-柱塞摩擦副的磨损状态而言，在试验条件下一般选取摩擦因数和磨损量作为正交试验的评价指标，但是本仿真考虑的工况下无法将摩擦因数作为参考评价指标，因此，选取60 s内瞬态动力学仿真中的最大摩擦应力和累计磨损体积作为正交试验的评价指标。

表6为单边间隙为0.05 mm时摩擦副参数优化表。为更直观地反映棒料的摩擦磨损状态，选取60 s内棒料摩擦应力和磨损体积作为正交试验的评价指标。利用综合平衡级差分析法[14]得到较优水平和因素主次，进而得到设计表中的最佳参数组合。表6中A、B、C、D分别代表正交试验的液体压力、涂覆层硬度、抽油杆冲程和液体润滑摩擦因数4个因素，k1、k2及k3分别表示因素的不同水平试验数据的均值，R为各因素对试验指标的极差值。通过极差值的大小分析，确定各因素对试验指标的影响程度，从而得出各因素主次。结合实际工况考虑如下原则：①在一定极差范围内，摩擦应力和磨损体积的值越小越好；②若摩擦应力和磨损体积不一致时，优先考虑因素对两个评价指标的主次关系，再对各水平组合进行合适的选取。

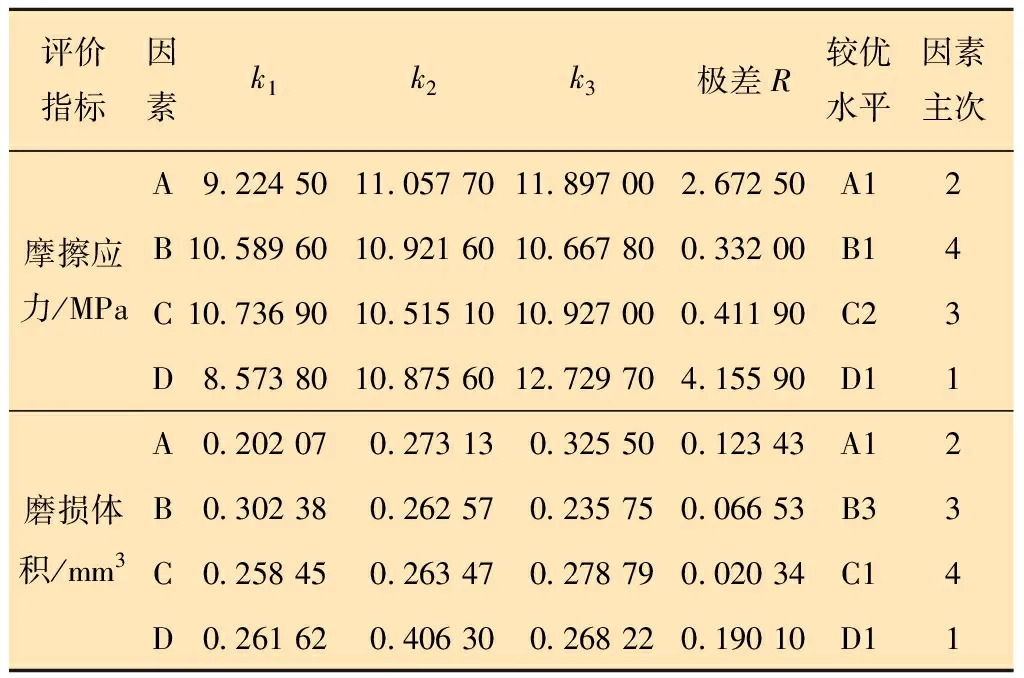
表6 单边间隙为0.05 mm时参数优化值

由表6可知，单边间隙为0.05 mm时，对摩擦副摩擦应力和累计磨损体积影响最大的两个因素为液体润滑摩擦因数和液体压力，其次是抽油杆冲程和涂覆层硬度。在仿真模型中，由于考虑接触变形，两摩擦副的接触表面的液体压力越大，摩擦副的接触面积越大，接触面的摩擦应力会减小，涂层表面磨损量也会增加。关于最大摩擦应力，较优水平一栏的组合为A1B1C2D1；而关于累计磨损体积的结果，较优水平一栏的组合为A1B3C1D1。因此液体压力均以取A1水平最好，液体润滑摩擦因数均以取D1水平最好。涂覆层硬度因素B对应力指标的影响程度排第4位，而对磨损体积的影响程度排第3位，且磨损体积取B3最好，B2次之，对2个指标进行综合考虑，最终涂覆层硬度因素水平B取B3较为合适。冲程因素C对摩擦应力指标的影响程度位居第3，而对磨损体积的影响程度位居第4，且磨损体积取C2差距并不大，综合考虑2个指标，最终冲程因素水平取C2效果较好。因此，当单边间隙为0.05 mm时，9组正交试验模型中最优方案为A1B3C2D1，即当液体压力为10 MPa，涂覆层硬度为1 150 MPa，抽油杆冲程为300 mm，液体润滑摩擦因数为0.11时，摩擦副减摩抗磨效果最好。

当单边间隙为0.08 mm时，正交试验数据分析如表7所示。由表7可以看出，在单边间隙为0.08 mm时，最大摩擦应力的结果在较优水平一栏的组合为 A1B2C1D1，而累计磨损体积的结果在较优水平一栏的组合为A1B3C1D1。与间隙值为0.05 mm的正交试验组比较可知，在累计磨损体积评价指标上，两组正交试验所得结果基本一致。因此，优先考虑磨损体积的影响对泵筒-柱塞摩擦副的磨损状况比较合理。在间隙值为0.08 mm模型中，较优水平一栏仅涂覆层硬度对评价指标存在较大影响。涂覆层硬度因素B对摩擦应力指标的影响程度排第4位，而对磨损体积的影响程度排第2位，且磨损体积取B3最优，且与B2差距很大。对两个指标进行综合考虑，最终涂覆层硬度因素水平B取B3。此处摩擦应力极差值分布不均的原因是正交试验模型7处的仿真结果可能出现了摩擦应力突变的情况，导致摩擦应力评价参数相差过大。因此，相对涂覆层硬度因素，优先考虑磨损体积评价指标。最终，当单边间隙为0.08 mm时，9组正交试验模型中的最优方案为 A1B3C1D1，即液体压力为10 MPa，涂覆层硬度为1 150 MPa，抽油杆冲程为150 mm，液体润滑摩擦因数为0.11时，摩擦副减摩抗磨效果最好。

表7 单边间隙为0.08 mm时正交试验数据分析

4 结 论

(1)改变摩擦副的配合间隙会对摩擦副的磨损状态产生较大影响，配合间隙越大，摩擦副的摩擦应力和磨损体积均显著增大，摩擦副的摩擦应力存在突变问题，磨损体积曲线的线性拟合效果较差。更改为较小配合间隙后，摩擦副整体磨损体积减小了10.05%且磨损状态有所改善，具体表现在摩擦应力无突变且磨损曲线线性拟合效果极佳。

(2)由9组正交试验模型结果分析可知，在单边间隙为 0.05 mm 时，60 s内泵筒涂覆层表面磨损体积为0.184 13～0.376 83 mm3。其中对摩擦副摩擦应力影响最大的因素是液体润滑摩擦因数，影响较大的因素是液体压力；对涂覆层磨损体积影响最大的因素是液体润滑摩擦因数。该间隙下正交试验的最优方案是A1B3C2D1，即当液体压力为10 MPa，涂覆层硬度为1 150 MPa，抽油杆冲程为300 mm，液体润滑摩擦因数为0.11时，摩擦副减摩抗磨效果最好。