海上钻井表层导管表面摩擦力变化机理研究*

胡南丁 杨 进 于 辰 包苏都娜 周健一 王佳康 丁益达

(中国石油大学(北京)安全与海洋工程学院)

0 引 言

表面摩擦力是影响海上钻井表层导管极限承载力的重要因素。表面摩擦力不仅是喷射过程中的阻力，而且是后续作业中井口载荷的支撑[1-3]。因此，国内外学者主要集中于表面摩擦力预测模型的研究[4-7]。但是，在深水钻井过程中仍然存在井口失稳下沉的安全事故，因此现有预测模型仍然存在不足之处。

改善模型不足之处的关键在于弄清表面摩擦力的变化机理。关于土体强度恢复机理方面已经有很多研究。A.E.CUMMINGS等[8]研究发现，隔水导管打桩过程中，初始阶段黏土的不排水剪切强度倾向于严重下降，随后会呈现随时间的延长而缓慢上升的趋势；O.ORRJE等[9]观察到隔水导管打桩过程中孔隙水压力的明显增加。但是，以上模型均建立在隔水导管打桩下入方法的基础上，没有分析喷射法下入隔水导管的过程。鉴于此，本文结合理论分析方法和现场模拟试验，探讨喷射过程中和喷射完成后表层导管表面摩擦力的变化机理，以期为表层导管的现场作业和后续研究提供理论依据。

1 表面摩擦力计算模型

在喷射完成之后，表层导管受到海床土层表面摩擦力的支撑作用，因此表层导管在垂直方向受力满足力学平衡：井口系统的重力与表面摩擦力和端部阻力之和相平衡(见图1)。

图1 表层导管受力分析图

海底土对表层导管的表面摩擦力可表示为：

Fl=fcS

(1)

式中：Fl为表面摩擦力，N；fc为单位面积表面摩擦力，Pa；S为表层导管与土体接触面积，m2。

根据深水区域的地质勘探结果，泥线以下0～100 m的土体主要由黏性土构成。表层导管下入深度一般小于100 m，因此以下推导均以黏性土为例。根据 API RP 2A-WSD(2002)[10]的相关准则，在表层导管任意一点的单位表面摩擦力为：

fc=ατf

(2)

式中：τf为不排水抗剪强度，Pa；α为无量纲系数，可由以下公式得出。

(3)

(4)

式中：ρ为第i层土体密度，kg/m3；g为重力加速度，m/s2；hi为第i层土厚度，m。

不排水抗剪强度τf计算式为：

τf=σ′tanφ+c

(5)

式中：σ′为土体有效应力，Pa；φ为内摩擦角，(°)；c为黏聚力，Pa。

因此，在喷射完成之后，表层导管的表面摩擦力可以表示为：

(6)

式中：D为表层导管直径，m。

根据公式(2)和公式(5)，在黏性土中表层导管表面摩擦力由不排水抗剪强度决定，而不排水抗剪强度与径向应力相关。为了探索表层导管表面摩擦力变化机理，首先要对径向应力的变化规律进行研究。

2 表面摩擦力变化机理分析

表层导管喷射之前土体的初始径向应力可以表示为：

σ=σ′+u0

(7)

式中：σ为土体骨架径向应力，Pa；u0为土体孔隙水压力，Pa。

表层导管喷射完成之后，土体固结过程中将产生过多的孔隙水压力，这将改变土体的径向应力。变化之后的径向应力可表示为：

σ=σ′+u0+Δu

(8)

式中：Δu为超孔隙水压力，即孔隙水压力的增加量，Pa。

将公式(8)代入公式(5)中可以得到土体的抗剪强度：

τf=σ′tanφ+c=(σ-u0-Δu)tanφ+c

(9)

由公式(9)可知超孔隙水压力的形成将使土体不排水抗剪强度减小，最终导致表面摩擦力下降。由于表层导管喷射下入速度对超孔隙水压力影响较小，所以不予考虑。

为了计算超孔隙水压力，应分析土体的应力状态(σ1、σ2、σ3为3个主应力)。在初始条件下，土体微元初始应力状态如图2所示。

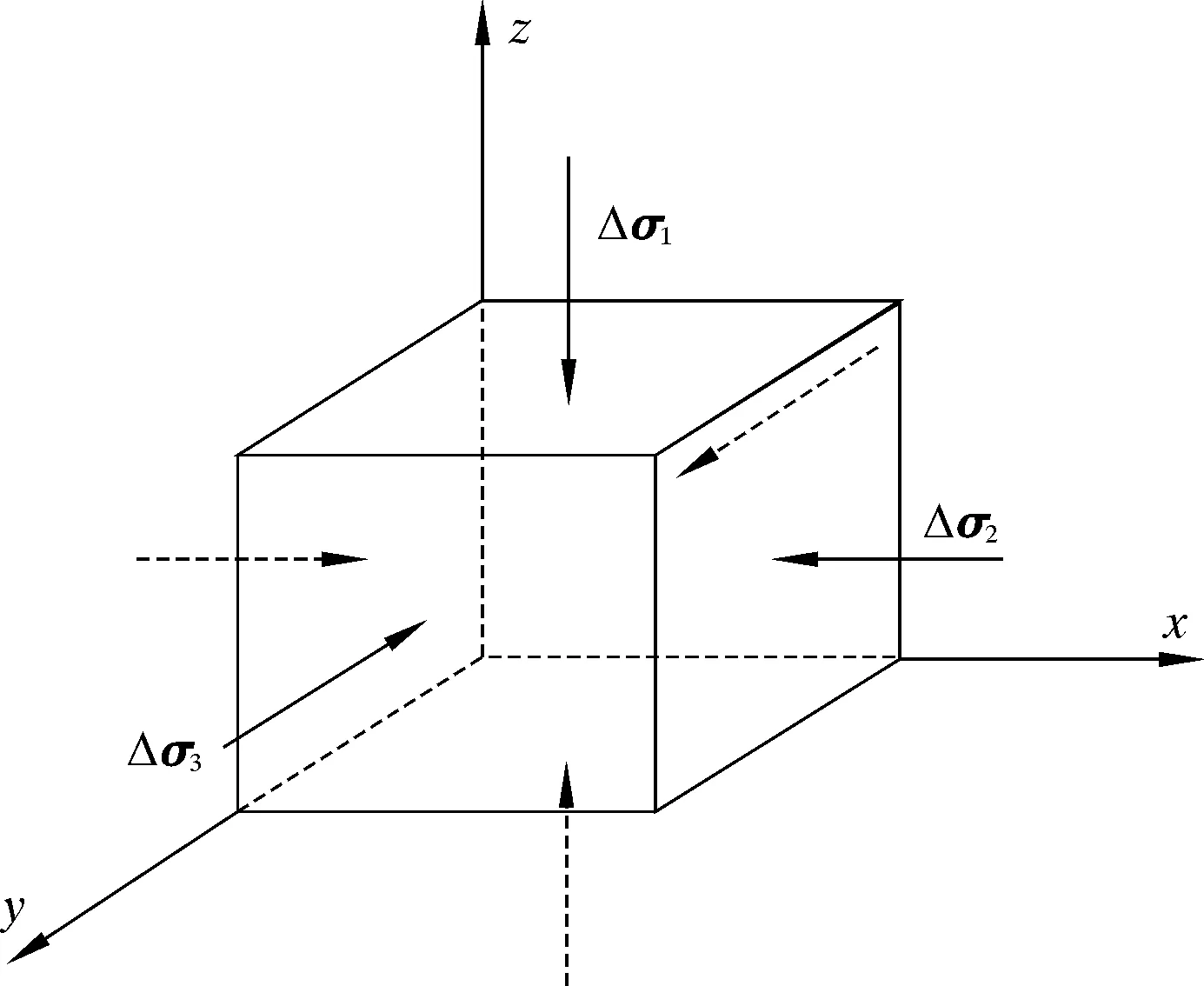
图2 土体单元初始应力

简单和轴向对称应力条件下，未扰动的土体应力状态为σ1>σ2=σ3。为了计算由外载荷引起的超孔隙水压力，将在该载荷下的土壤微元体分为两部分：各向同性应力状态(球应力状态)和偏应力状态。在各向同性应力条件下，土体在3个方向受到相同应力的压缩效应。此种作用在土体中产生过多的孔隙水压力ΔuB。在偏压应力条件下，土体受到偏压应力的压缩而产生过多的孔隙水压力ΔuA。ΔuA和ΔuB之和为喷射过程中外部载荷引起的孔隙水压力增加量Δu，如图3所示。

图3 土体单元各向同性应力与偏应力

对于各向同性应力部分，基于有效应力原理，各向同性压缩引起的有效应力的增加量可写为：

(10)

式中：Δσ1、Δσ2、Δσ3为各向主应力增加量，Pa；Δσ1′、Δσ2′、Δσ3′为变化后的各向主应力增加量，Pa；ΔuA为偏应力引起的超孔隙水压力，Pa；ΔuB为各向同性应力引起的超孔隙水压力，Pa。

ΔVs=εvV0

(11)

式中：ΔVs为土壤微元体体积的变化量，m3；εv为土体微元体总应变，无量纲；V0为土体微元体初始体积，m3。

假设土体的骨架是弹性，根据弹性理论，土体微元体总应变εv可以表示为：

(12)

式中：E为土体微元体弹性模量，Pa；υ为土体微元体泊松比，无量纲。

将式(12)代入式(11)得体积压缩量：

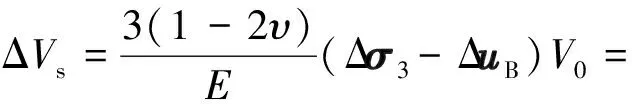
Cs(Δσ3-ΔuB)V0

(13)

式中：Cs为土体压缩系数，无量纲。

由孔隙水压力增加引起的体积变化为：

ΔVv=CfΔuBnV0

(14)

式中：ΔVv为土体孔隙流体体积变化量，m3；Cf为孔隙流体压缩系数，无量纲；n为第n层土体。

在不排水条件下，土体骨架中孔隙体积和孔隙水的体积变化应相等(ΔVv=ΔVs)，结合公式(13)和公式(14)得到孔隙水压力计算公式：

(15)

因海底土已经饱和，孔隙充满了海水，另外孔隙流体的压缩系数远小于土体的压缩系数，所以深水条件下的公式(15)可简化为：

ΔuB=Δσ3

(16)

基于同样的原理，偏应力部分的孔隙水压力增量可以表示为：

(17)

方程(18)根据土体弹性假设而得到，但是实际上土体在承受剪切应力的同时，其会膨胀或压缩。因此，引用A.W.SKEMPTON[11-12]在研究中得到的土体膨胀修正系数改进方程(17)，于是可以得到：

ΔuA=A(Δσ1-Δσ3)

(18)

式中：A为土体膨胀修正系数，无量纲。

因此，由外加载荷引起的超孔隙水压力计算公式为：

Δu=ΔuB+ΔuA=Δσ3+A(Δσ1-Δσ3)

(19)

在表层导管喷射下入过程中，由于海水的压缩性较小，土体固结时孔隙水压力将增大。根据太沙基模型中的有效应力理论：当孔隙水压力增大时，岩石骨架的有效应力将减小，从而导致周围土体对表层导管的表面摩擦力下降；当表层导管喷射完成之后，孔隙中的水将会从孔隙中流出或渗出，形成的超孔隙水压力将会消散。根据有效应力理论，当超孔隙水压力消散时，土体的有效应力将会上升从而导致表面摩擦力增大。

3 现场模拟试验

为了探索和研究表层导管与海底土层之间表面摩擦力的变化机理，设计和制作了一套模拟喷射下入设备。现场模拟试验方案如图4所示。

图4 现场模拟试验方案

试验原理是通过测量喷射完成之后土体径向应力和孔隙水压力，得到表层导管表面径向应力和孔隙水压力的变化规律。试验采用了ø244.5 mm(9in)套管来模拟实际作业中的表层导管。在表层导管侧面对应三种土层的位置焊接9个压力传感器，通过喷射的方式将导管下入海底土层中。土层参数见表1。喷射完成后，持续测量导管周围土体径向应力和孔隙水压力随时间的变化规律。

表1 试验场地土层参数

喷射完成后持续监测土体径向应力和孔隙水压力，土层受力随静置时间的变化曲线如图5～图7所示。

图5 1.80～1.95 m粉土层受力随静置时间的变化曲线

图6 2.80～2.95 m黏土层受力随静置时间的变化曲线

图7 3.80～3.95 m泥质黏土层受力随静置时间的变化曲线

从试验结果中可以看出3种特征：①径向应力传感器测试的结果明显要高于其他传感器压力；②对于孔隙水压力，相同层位的孔隙水压力有着一开始增大随后减小的趋势；③对于有效应力(骨架应力)，随着孔隙水压力的增大而有效应力减小，同时随着孔隙水压力的减小而有效应力开始增大。

4 表面摩擦力随静置时间的变化规律

为了研究喷射完成后表层导管表面摩擦力随静置时间的变化规律，在同样的场地进行了另外一组试验。将表层导管喷射下入至泥线以下5 m的土壤中，并静置不同的时间后上提。当表层导管有明显位移时测量其上提力最大值并计算表面摩擦力，同样静置时间t下表面摩擦力测量3组。试验数据如表2和表3所示。

表2 表面摩擦力测量结果(0.5～6.0 h) kN

表3 表面摩擦力测量结果汇总(8～96 h) kN

在现场试验中，表面摩擦力在两个时间点起到了重要的作用。第一个时间点是没有连接CADA工具(表层导管送入工具)，此时井口压力较低；第二个时间点是表层导管安装过程。在这两个时间点，所有水下井口系统的重力都由表层的侧向摩擦力承担。根据实际钻井过程，表面摩擦力测量数据被分成两组进行分析。

图9 表面摩擦力随静置时间(0～96 h)的变化规律

从图8可以看出，在前12 h内，表面摩擦力随静置时间的延长而增大。但是增大速率从低到高，而不是固定的。这是因为在恢复的初始阶段，土壤压实效果较差，在此基础上形成的超静孔隙水压力和土壤的抗剪强度较低。因此，恢复速率并不明显，随着时间的延长，底层土体开始固结，超静孔隙水压力的消散将导致土体的抗剪强度增大。因此，表面摩擦力的恢复速率将会随着时间的延长而增大。

图8 表面摩擦力随静置时间(0～12 h)的变化规律

表层导管的表面摩擦力也随着时间的延长而增大。这个趋势反映了超静孔隙水压力的消散过程和土体抗剪强度增大的过程。但是附加的表面摩擦力很小，并且在72 h之后变化开始变得平缓。因此，在现场作业中，表层导管喷射到位之后的静置时间至少为72 h。

5 结 论

(1)通过分析喷射过程中土体应力以及测量表层导管喷射过程中径向应力和孔隙水压力的变化情况，揭示了表层导管表面摩擦力的变化规律。

(2)表层导管喷射下入方法中由于土体体积压缩造成的超孔隙水压力的形成和消散是表面摩擦力变化的主要原因。

(3)在喷射过程中形成超孔隙水压力，使得有效应力降低，从而导致表层导管表面摩擦力减小；喷射完成后随着超孔隙水压力的消散，有效应力升高，表层导管表面摩擦力增大。

(4)表层导管喷射完成之后，在最初的12 h，表面摩擦力的恢复与时间呈非线性关系。72 h之后，表面摩擦力增大幅度开始变小，并且趋势变缓。因此，在现场作业中，表层导管喷射到位之后的静置时间至少为72 h。