基于相关系数法的彩色图像立体匹配方法

孔维哲

（1.长江重庆航道局，重庆 401147）

图像匹配是图像信息处理领域中一项极为基本和重要的技术，其应用领域已逐步从原来单纯的军事应用扩展到其他领域，尤其在数字摄影测量、计算机视觉、模式识别中应用更为广泛[1]。数字摄影测量与传统的模拟摄影测量以及解析摄影测量有着明显的不同，主要体现在数字摄影测量不是影像存储设备，而是自动化处理流程，影像匹配是不可忽视的核心技术。实际生活中的图像非常复杂，而且纹理特性十分明显，匹配错误的现象时有发生。精准快速地发现不正确的匹配点、提高匹配结果的精准度是一项重要的工作。当匹配模式不同时，其优势和缺陷也存在很大的区别，当前匹配方法有地形连续控制策略[2]、最小二乘匹配方法、整体松弛匹配方法[3]等多种类型。

本文在研究过程中将相关系数当成匹配测度，对同一个影像的不同波段实施粗匹配，并对相关结果实施对比分析，删除错误的匹配点，在这个初值的基础上，使用最小二乘匹配实施亚像素匹配，从而获取一个精度较高的匹配结果。

1 基本原理

1.1 特征点提取

应用频率较高的点特征提取算子包括Moravec 算子、Harris 算子、Susan 算子等多种类型，Harris 算子的计算流程比较简单、计算内容比较少、计算效率比较高，应用最为广泛，在纹理复杂程度较低的区域中只能提取很少的特征点；稳定性高，就算目标图像出现一些旋转、噪声或者灰度变化，也可以充分有效的提取特征点[4]。本文主要使用Harris 算子，其原理是:首先对影像进行一阶差分进而核算出每个像素的平均平方梯度矩阵M，而梯度矩阵M的特征值就可被认定为自相关函数的曲率。该算子通过对特征值的比较可以做如下分析:①假设2 个特征值的大小存在很大的差距，可以将这些点当成影像中的边界值；②假设2 个特征值的差距不大而且2 个数值都比较小，可以将这个点当成非角点；③假设2 个特征值的差距很大且2 个数值都比较大，意味着影像点在任意方向上的灰度曲率都非常大，可以将这些点当成角点或特征点。

Harris 算子的一般处理过程如下:

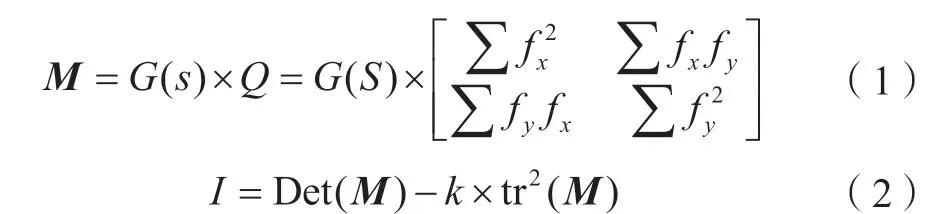
式中，gx指代的是原始影像点沿x方向得出的梯度图；gy指代的是原始影像点沿y方向的计算出的梯度图；G(s)指代的是高斯卷积滤波；Det(M)指代的是矩阵M的行列式，tr(M)指代的是矩阵M的直迹。k指代的是0.1 以下的小值常数。I中的所有元素值对应的原影像的兴趣值，假如该值超出了区间范围，可以将这个影像点看成所求角点。

Harris 算子的步骤:

1）核算影像上的所有像素点在水平以及竖直方向上的一阶导数，并计算出相应的乘积，并以此为基础绘制出图像gx，gy和gxy。

2）借助高斯滤波对步骤1 中的3 个图像实施卷积处理，进而得到原图像所有像素点的兴趣值。

3）选择局部极值点。Harris 表示:特征点是特定区间内的兴趣值极大位置的相应像素点，当获取每个像素点的兴趣值以后，应该将各个局部兴趣值最大的像素点统计下来。在核算过程中，逐个计算出以各个像素为核心的窗口中心点像素的最大值，那么这个点就是特征点。

4）参考实际需求选择特定数量的特征点。局部极值兴趣值的像素点数量非常多，会大大降低核算效率，利用排序方法确定一个区间（通常选取全局最大极值的1/1 000-1/10 000）对所有极值点实施筛选处理，最终得到一些特征点。

1.2 匹配测度

现状的影响匹配测度通常使用以灰度信息为基础的匹配准则。应用频率较高的测度方法有差绝对值和、协方差函数、差平方和等[5]。此外相关系数与相关系数测度存在较强的一致性，实时处理能力十分突出，所以这种测度方法的应用频率非常高[6]。本文在研究过程中将使用相关系数，相关原理如下所示:

相关系数应用过程中，第一步要核算出2 个图像信号的协方差函数；第二步除以2 个图像的方差获取标准协方差函数；影像g（x,y）、g′（x′,y′）的相关系数如下所示:

1.3 单点最小二乘匹配

要想进一步提高亚像素级的匹配精度，需要将粗匹配结果当成初始值并实施最小二乘匹配。这种方法能够综合分析2 个影像之间的几何变形、灰度变形等。在线性化处理之后，获取最小二乘匹配的误差函数。法化后整体平差获取准确的较高的同名点[7]。

正常情况下，影像匹配目标窗口的尺寸非常小，因此在单点最小二乘匹配过程中仅仅考虑一次几何形变就可以了。

式中，未知数dh0,dh1,da0,da1,da2,db0,db1,db2为待定参数的改正值，它们的初值有粗匹配给定。观测值Δg是左右影像相应像素的灰度差。

2 彩色图像的分波段匹配

正常情况下影像匹配处理的都是灰度图像，如果要对彩色图像实施匹配处理，要先进行灰度化处理，应用频率较高的彩色影像灰度化方法有2 种:

1）均值法:将彩色图像中的RGB 3 个分量图像的亮度值进行平均。

2）加权平均法:参考影像的重要等级以及特殊需求，对RGB 3 个分量图像以不一样的权值实施加权平均处理。

在对灰度化图像进行粗匹配后，需要先进行剔除误匹配，传统的剔除误匹配点的方法是采用RANSAC算法[9]，利用改进的RANSAC 算法不仅在效率上有所提高，而且能够剔除更多的误匹配对[10]。但是RANSAC 算法较为复杂，本文利用彩色图像的性质提出了一种新的剔除误匹配的方法:彩色图像的3 个波段分量可以看作3 幅不同的图像，它们各自的灰度信息有差别，空间信息却是完全相同的，同一个特征点在3 个波段影像上的位置应该是完全相同。依次对3 个波段影响实施匹配核算，不同波段的左右影像中的同名点位置也应该是一模一样的。如果某一波段影像出现了误匹配，那么同一点在3 幅影像上的匹配结果会有较大的差异。3 个波段影像在同一点出现误匹配且结果相近的概率非常小，它们的匹配结果仍然会有较大的差异。因此通过对3 个波段分别进行匹配的方法，能够剔除绝大部分的误匹配点。

3 实验结果与分析

本次实验选取的是2 幅800×800 的彩色影像，原始数据如图1。本文实验有如下过程:

图1 原始图像

1）借助Harris 算子获取影像中3 个波段的特征点，兴趣值窗口大小为5×5，特征点计算窗口大小是7×7。

2）用相关系数法对3 个波段影像选取11×11 的目标窗口大小，相关系数阈值取0.95 进行匹配。

3）将3 个波段的匹配结果进行比较，剔除误匹配点。

4）将原始图像灰度化，将约束后的粗匹配结果作为初值用最小二乘法进行精匹配。

实验结果如下:

红光波段粗匹配工作结束之后，得到1 620 对匹配点，具体内容如图2；绿光波段粗匹配工作结束之后，得到1 704 对匹配点，具体内容如图3；蓝光波段粗匹配工作结束之后，得到1 724 对匹配点，具体内容如图4。

图2 红光波段匹配结果

图3 绿光波段匹配结果

图4 蓝光波段匹配结果

3 个波段的粗匹配完成后，需要对匹配结果进行约束。理论上，匹配正确的点位置应该是完全相同的，但是由于图像的复杂性，不可避免会出现一定的偏差，本次实验将3 个波段匹配结果相差在2 个像素内的点都予保留，相差在3 个或者以上的，认为是误匹配点，将其剔除，这样就剩余655 对匹配点，表1 列举了10 对被剔除的点。

表1 剔除的点信息

以余下的655 对匹配点作为初值，对原始彩色图像加权灰度化，进行最小二乘精匹配，余下59 对同名点，匹配结果如图5 所示。

图5 最小二乘匹配结果

4 结 语

影像匹配是数字摄影测量和计算机视觉中不可或缺的核心技术，对两者的自动化水平有着决定性的影响。本文对彩色图像3 个波段分别进行匹配，然后比较它们之间的差值，以此为约束条件，对粗匹配结果进行约束，有效地剔除了误匹配点，为最小二乘精匹配提供了精确的初值，提高了匹配的精度，是一种比较有效的匹配方法。