夹具对高压绝缘电缆热学特性影响的有限元分析
吕安强 李 静 张振鹏 宋 贺 林晓波
夹具对高压绝缘电缆热学特性影响的有限元分析
吕安强1,2李 静3张振鹏4宋 贺1林晓波5
(1. 华北电力大学电子与通信工程系 保定 071003 2. 华北电力大学河北省电力物联网技术重点实验室 保定 071003 3. 华北电力大学计算机系 保定 071003 4. 中国电力科学研究院有限公司 武汉 430074 5. 国网浙江省电力有限公司舟山供电公司 舟山 316021)
夹具是已敷设高压绝缘电缆线路中的必备组件,为了获得夹具对缆体热学特性的影响,以典型220kV交流单芯交联聚乙烯(XLPE)绝缘电缆为对象进行电热耦合有限元分析。按照国内某市电缆的实际敷设情况,建立电缆在五种不同材料夹具下的二维和三维电热耦合有限元模型,通过稳态和暂态热力学计算,获得电缆在不同夹具下的载流量和热时间常数;通过计算不同夹具材料和间隔下的电缆温度,得到导体温度在径向和轴向的分布规律,并获得夹具材料和间隔距离与电缆导体温度的关系函数。结果表明,夹具的材料和间隔距离对电缆的载流量和热时间常数都有影响,夹具的热导率和间隔距离都存在一个临界值,在该值两侧导体温度变化存在较大差异。该文研究可为电缆的施工和运维提供理论和数据支持。
夹具 高压电缆 载流量 热时间常数 有限元
0 引言
高压输电电缆作为城市能源输送的重要通道,在电力系统中起着不可或缺的作用,一旦出现故障,会导致严重的社会和经济损失[1-2]。电缆在输送电力时会因导体损耗而发热,现在普遍使用的交联聚乙烯(Cross-Linked Polyethylene, XLPE)绝缘电缆对导体运行温度有严格要求,为了保证绝缘寿命,电缆长期工作温度不能高于90℃[3-6]。在电缆的实际敷设过程中,需要用夹具固定电缆,使用不同材料的夹具会对夹持部分电缆的内部温度分布产生影响,选择或使用不当会导致电缆内部温升上升严重,成为电缆载流量的瓶颈[7-11]。
目前,国内外学者都对高压电缆进行了电热有限元建模研究。林晓波等对三芯光纤复合海底电缆超负荷运行时的温度变化情况进行了仿真[12]。李昭红对高压直流XLPE绝缘电缆中间接头进行了电热耦合仿真研究,并对稳态载流量进行了计算[13]。张洪麟等利用对分法对直埋单芯电缆的温度场分布和载流量进行了迭代求解[14]。梁永春等利用有限元法对地下排管敷设电缆群的暂态温度场和短时载流量进行了仿真计算[15]。张尧等利用暂态热路模型对空气敷设和直埋敷设单芯电缆的热时间常数进行了计算[16]。P. Oclon等对平行排列的地下输电线路进行了热分析,详细讨论了土层温度影响下热导率的计算方法[17]。吕安强等在建立三芯海缆热路模型的基础上,建立了光纤与导体的温度关系方程,并用有限元求解结果验证了方程的正确性[18-19]。目前,国内外学者还没有研究电缆夹具对电缆载流量、热时间常数和缆体热分布的影响。
本文以220kV交流单芯XLPE绝缘电缆为研究对象,针对不同夹具材料分别进行了电缆电热有限元建模和求解,分析了不同夹具对电缆载流量、热时间常数和缆体温度分布的影响,为充实IEC 60287载流量计算方法、城市大容量输电线路敷设施工与设计提供参考。
1 工程现场情况
陆地电缆的实际敷设情况如图1所示,电缆采用蛇形敷设,垂直排列安装在桥架上,缆体暴露在户外空气中,年极限最高温度为40℃。夹具可选材料包括铝合金、复合材料(不饱和聚酯膜塑料)、玻璃钢、阻燃尼龙、胶木(酚醛聚酯)。
电缆内部结构及各层名称如图2所示,缆体由内到外依次为铜导体、导体屏蔽、XLPE绝缘、绝缘屏蔽、缓冲阻水层、铝护套和PP外披层,铜导体由导电圆单线逐层绞合而成。

图1 工程现场照片

图2 电缆内部结构及各层名称
电缆的尺寸和各层结构的材料参数见表1和表2。
表1 电缆尺寸参数
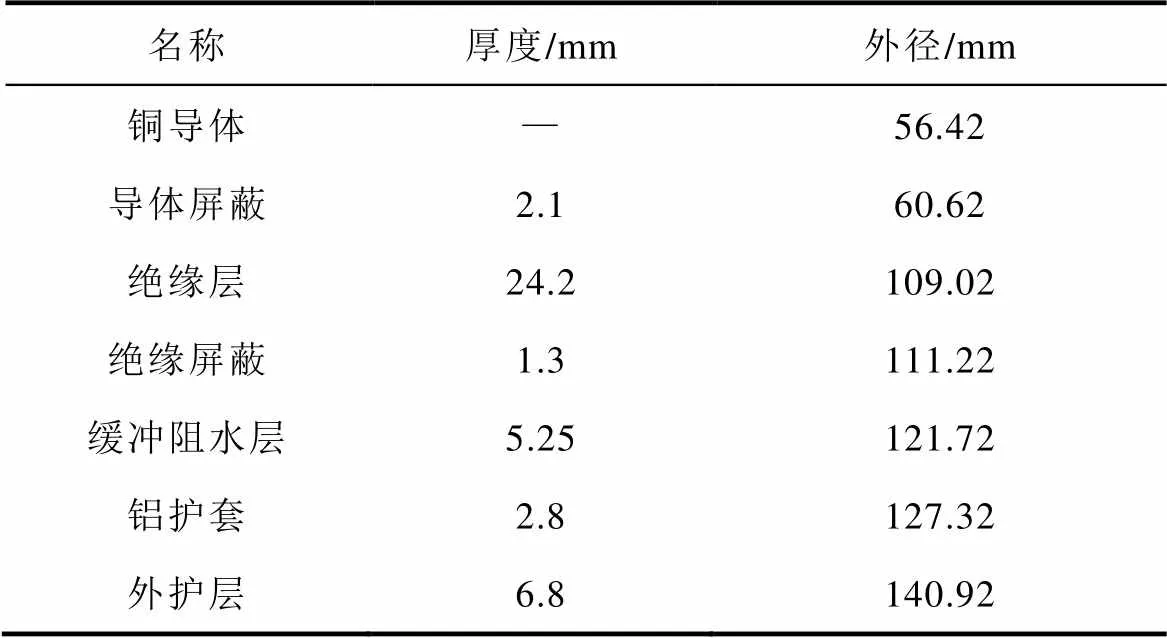
Tab.1 Cable size and parameters
表2 电缆和夹具材料参数

Tab.2 Materials parameters of cable and clamps
2 有限元模型
2.1 几何模型
为了保证模型计算的准确性和效率,减少非电热因素对模型的影响,首先对模型进行简化。构成导体的单丝采用紧压结构,且铜是热的良导体,所以在热力学模型中可将其看作是一个实心圆柱;导体屏蔽、XLPE绝缘和绝缘屏蔽电热特性相似,且导体屏蔽和绝缘屏蔽很薄,故将这3层合并,统称为绝缘层;铝也是热的良导体,将铝护套的波纹结构简化为圆环;电缆夹具一般为上、下两个夹片,实际使用过程中两夹片会贴合到一起,故将其简化为一个整体。根据现场夹具形状,确定简化后的电缆和夹具模型结构如图3所示。

图3 简化后的电缆和夹具模型结构
2.2 有限元设置
实际运行电缆采用三相交叉互联,铝护套上的电流近似为零,因此忽略铝护套发热,只考虑导体损耗发热。本文选择包含电压、温度自由度的三维单元类型SOLID226单元,该单元共有20个节点,每个节点有UX、UY、UZ、TEMP和VOLT 5个自由度,可用于导体的热电耦合分析;选定SOLID90单元构建其他结构层,该单元为20节点热敏元件,每个节点只有温度自由度;以上两种单元类型都可完成稳态和暂态热学分析,满足分析要求。
本文在ANSYS中采用自由网格划分方式,设定智能网格划分等级为6,得到电缆模型网格划分效果如图4所示。由图看见,网格形状规则、密度适中、分布均匀,满足计算精度的要求。
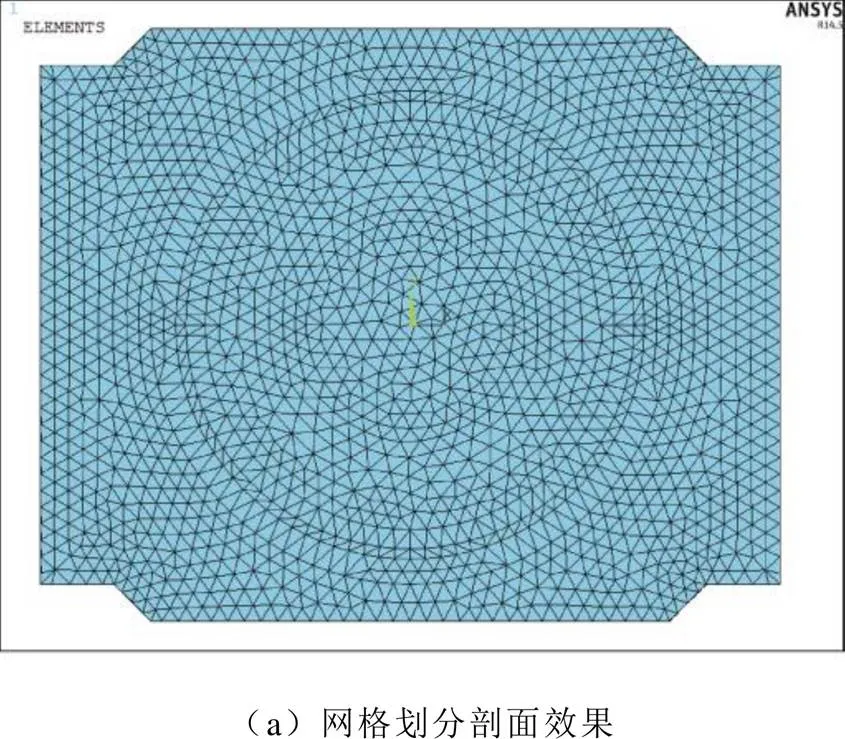
分析电缆的实际敷设情况发现,电缆直接暴露在空气中,上部设有顶棚,电缆外表面与周围的空气存在对流换热和热辐射,电缆的初始温度状态与环境温度相同。夹具材料包括铝合金、玻璃钢、复合材料、阻燃尼龙和胶木五种,电缆与夹具之间存在热传递,夹具与空气存在自然对流换热和热辐射。
设定电缆模型长度为2.1m,夹具在电缆中间。限制导体左端面的电压自由度为0V,并对该截面的中间节点分别施加载流量电流载荷和周期负荷电流载荷。电缆采用三相交叉互联接地形式,铝护套上不施加电流。环境温度设为40℃,空气的对流传热系数设为7W/(m2·℃)。
3 结果分析
3.1 载流量分析
电缆内发热量最大的部件是导体,运行中的电缆,在直径方向由内向外温度递减,最接近导体位置的XLPE绝缘温度最高。IEC 60287标准规定,XLPE绝缘材料长期工作最高允许温度为90℃,并定义该温度下导体电流为电缆的载流量。由于导体屏蔽很薄,可近似认为它和绝缘内侧温度一致,因此,将导体达到90℃时的电流作为电缆的载流量。
载流量受敷设方式、环境因素影响。常规的电缆设计规程中,一般不考虑夹具的影响,只根据电缆结构和环境参数进行计算。本文所研究的蛇形敷设,电缆暴露在空气中,空气最高温度为40℃。夹具间隔最大不超过4m,根据现场情况进行调整。在转弯处和容易移动的位置,有必要连续小间隔放置多个夹具,此处有可能成为温度的瓶颈点。为了获得夹具对载流量的影响,本文分别建立了五种材料夹具下的电缆稳态电热耦合模型,以导体温度达到90℃为基准,计算它们的载流量,得到有限元求解结果如图5所示,载流量数据见表3。

表3 不同材料夹具下电缆的载流量

Tab.3 The ampacity ratings of cables under different material clamps
由图5可知,导体温度为90℃时,缆体各层结构及外层夹具的温度是不同的,铝合金夹具的温度最高,胶木夹具的温度最低,二者相差近10℃。由表3可知,夹具对载流量有一定的影响,胶木和阻燃尼龙使载流量分别下降了150A和120A,而玻璃钢、复合材料和铝合金却使载流量分别上升了20A、70A和270A。可见,夹具对载流量的影响是不可忽视的,胶木和阻燃尼龙夹具有可能成为载流量的瓶颈点。
3.2 热时间常数分析
现场运行的电缆负荷电流是变化的,由于电缆内部热容的影响,缆体温度变化会发生滞后。常用热时间常数来反映电缆导体温度变化的快慢,进而判断负荷变化对绝缘温度的影响,热时间常数是电缆系统的重要特性参数之一[18]。定义热时间常数为电缆通入电流后,导体由初始温度升至总温升量的63.2%所用的时间,导体的最高温度为90℃。
设置两种典型环境温度20℃和40℃,对五种夹具下的电缆进行暂态电热有限元求解,分别施加各自的载流量,使导体温度从环境温度升高至90℃,提取不同时刻的导体温度,绘制导体温度随时间变化的曲线,如图6所示。由图可知,使用不同材料夹具的电缆分别施加各自的载流量负荷电流后,导体的温度最后稳定时都是90℃。对于任意一条曲线来说,它的斜率都是先大后小,说明温度的上升速度都是先快后慢。在纵轴某一温度处(如70℃),使用导热性能好的夹具的电缆,虽然更容易散热,但由于其载流量增加了,所以温度上升地更快,到达某一温度处需要的时间更短;在横轴某一时间处(如第5小时),使用导热性能好的夹具的电缆,虽然更容易散热,但由于其载流量增加了,所以到达的温度更高。由于电缆带上夹具后,其热阻、热容参数发生了变化,所以无夹具电缆的曲线与带夹具的曲线变化趋势有差异,无夹具曲线与其他曲线出现了交叉。综合来看,不同材料夹具对热时间常数的影响存在差异,铝合金、复合材料、玻璃钢、阻燃尼龙和胶木的热时间常数依次增加,这与载流量计算数据是对应的,说明夹具的导热性能越好、载流量越大、热时间常数越小。
根据热时间常数的定义,初始环境温度为20℃和40℃时的热时间常数即导体温度达到64.2℃和71.6℃时所需的时间。从曲线中提取相应的时间,并列于表4中。由表4可知,不同环境温度下,相同夹具的电缆热时间常数相差不大,原因在于热时间常数只与电缆材料和周围环境的热阻和热容有关,与环境温度无关。

图6 各夹具下电缆的热时间常数曲线
表4 设计额定载流量下不同材料夹具内导体的温度

Tab.4 The conductor temperature in different material clamps under designed ampacity ratings
实际工程中,固定电缆的夹具随敷设路由按一定间距布放,在直线敷设时,间距一般较大,在拐弯处间距会变小,间距的变化可能会导致导体温度的更复杂变化。以胶木夹具为例,按照0.01m、0.1m、0.2m、0.3m、0.4m、0.5m、0.6m、1.0m、1.2m间距分别建立三维电热有限元模型,胶木夹具取不同距离时的温度分布如图7所示。由图可知,在3 080A的设计载流量下,随着夹具间距的增加,导体温度逐渐降低,当夹具间距达到1.2m时,导体温度接近90℃,即与无夹具电缆基本一致。这是因为,随着夹具间距的增加,夹具两侧的电缆长度变大,由于电缆各层的热导率高于胶木,所以夹具内的热量会通过夹具两侧电缆散发出去;而当两个夹具的距离太近时,电缆不能有效散热,导致导体温度高于90℃。
为了确定夹具之间的距离和热导率与导体温度的关系,选择具有不同热导率的夹具并在不同的距离处进行有限元模拟,得到关系曲线如图8所示。从图可知,当夹具距离小于0.5m后,随着距离的缩短,夹具内导体温度急剧上升。当夹具热导率为0.5W/(m·℃)时,夹具之间的距离对导体温度基本没有影响;高于0.5W/(m·℃)时,随着夹具之间的距离减小,导体温度逐渐降低;小于0.5W/(m·℃)时,夹具距离减小,导体温度会升高。这说明,0.5W/(m·℃)的热导率是导体温度-夹具距离曲线的转折点,实际工程中应尽量选用热导率大于0.5W/(m·℃)的材料制作夹具。如果夹具的热导率小于0.5W/(m·℃),应注意控制夹具距离。

图7 胶木夹具取不同距离时的温度分布

图8 不同材料夹具距离与温度的关系
以胶木夹具为例,其热导率为0.27W/(m·℃),提取不同间距下夹具内的导体温度,利用最小二乘法拟合曲线,可得到导体温度和夹具间距的关系为

式中,为导体温度(℃);为夹具间距(m)。
实际工程中,可根据式(1)计算夹具的最小距离,以防止导体过热导致的电缆寿命降低。
4 结论
夹具普遍用于陆地高压电缆的敷设工程中,不同材料的夹具对电缆的热特性有影响,夹具材料和间距选择不合适会影响电缆的绝缘寿命,通过研究得出以下结论:
1)铝合金、复合材料和玻璃钢这些热导率高于0.5W/(m·℃)的材料制成的夹具能提高电缆的载流量,阻燃尼龙、胶木等热导率低于0.5W/(m·℃)的材料制成的夹具会降低电缆的载流量;载流量的变化和材料热导率成同相单调关系。
2)电缆热时间常数与环境温度无关,只决定于电缆的热阻和热容,夹具对该参数有影响,夹具材料的热导率越低,电缆的热时间常数越大,越不能快速散热。
3)夹具的间距和热导率对导体温度有影响,在一定负荷电流下,夹具间距越小,热导率越小,夹具内导体温度越高;存在一个距离临界值,当夹具间距小于0.2m,热导率小于0.5W/(m·℃)时,导体温度会大幅上升,工程中应尽量选取热导率较好的夹具,并使夹具间距大于0.2m;若间距确需小于0.2m,应选用热导率大于0.5W/(m2·℃)的夹具。
[1] 谢声益, 杨帆, 黄鑫, 等. 基于太赫兹时域光谱技术的交联聚乙烯电缆绝缘层气隙检测分析[J]. 电工技术学报, 2020, 35(12): 2698-2707.
Xie Shengyi, Yang Fan, Huang Xin, et al. Air gap detection and analysis of XLPE cable insulation based on terahertz time domain spectroscopy[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(12): 2698-2707.
[2] 黄光磊, 李喆, 杨丰源, 等. 直流交联聚乙烯电缆泄漏电流试验特性研究[J]. 电工技术学报, 2019, 34(1): 192-201.
Huang Guanglei, Li Zhe, Yang Fengyuan, et al. Experimental research on leakage current of DC cross linked polyethylene cable[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 192-201.
[3] 王鹤, 李兴宝, 路俊海, 等. 基于叠加原理的光纤复合低压电缆热路模型建模[J]. 电工技术学报, 2019, 34(7): 1381-1391.
Wang He, Li Xingbao, Lu Junhai, et al. Modeling method of OPLC thermal circuit model based on superposition principle[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1381-1391.
[4] 林晨炯, 林珍, 吴雅琳. 电缆接头温度在线监测方法研究综述[J]. 电气技术, 2019, 20(5): 1-4, 9.
Lin Chenjiong, Lin Zhen, Wu Yalin. Summary of research on online monitoring method of cable joint temperature[J]. Electrical Engineering, 2019, 20(5): 1-4, 9.
[5] Benato R, Dambone S S, Forzan M, et al. Core laying pitch-long 3D finite element model of an AC three-core armoured submarine cable with a length of 3 metres[J]. Electric Power Systems Research, 2017, 150: 137-143.
[6] Juan Carlos Del-Pino-López, Hatlo M, Cruz-Romero P. On simplified 3D finite element simulations of three-core armored power cables[J]. Energies, 2018, 11(11): 3018.
[7] Lü Anqiang, Li Jing, Li Yongqian. Research on strain and temperature measurement of OPGW based on BOTDR[C]//International Conference on Optical Instru- ments and Technology: Optical Sensors and Appli- cations, Beijing, China, 2013: 90441H-1-90441H-7.
[8] Vollaro R D L, Fontana L, Vallati A. Thermal analysis of underground electrical power cables buried in non-homogeneous soils[J]. Applied Thermal Engineering, 2011, 31(5): 772-778.
[9] IEC 60287-1-1-1994 Calculation of the current rating of electric cables, part 1: current rating equations (100% load factor) and calculation of losses, section 1: general[S]. London, 1994.
[10] IEC 60287-1-2-1993 Calculation of the current rating of electric cables, part 1: current rating equations (100% load factor) and calculation of losses, section 2: sheath eddy current loss factor for two circuits in flat formation[S]. Switzerland, 1993.
[11] IEC 60287-2-1-1994 Calculation of the current rating of electric cables, part 2: thermal resistance, section 1: calculation of thermal resistance[S]. London, 1994.
[12] 林晓波, 何旭涛, 陈国志, 等. 三芯光纤复合海底电缆超负荷运行有限元建模[J]. 光通信研究, 2018(1): 23-26.
Lin Xiaobo, He Xutao, Chen Guozhi, et al. Finite element modeling of overload operation of three-core fiber composite submarine cable[J]. Study on Optical Communications, 2018(1): 23-26.
[13] 李昭红. 高压直流XLPE绝缘电缆中间接头电热耦合仿真研究和稳态载流量计算[D]. 广州: 华南理工大学, 2016.
[14] 张洪麟, 唐军, 陈伟根, 等. 基于有限元法的地下电缆群温度场及载流量的仿真计算[J]. 高压电器, 2010, 34(3): 42-45,51.
Zhang Honglin, Tang Jun, Chen Weigen, et al. Simulation calculation of temperature field and current carrying capacity of underground cable group based on finite element method[J]. High Voltage Apparatus, 2010, 34(3): 42-45, 51.
[15] 梁永春, 闫彩红, 赵静, 等. 排管敷设电缆群暂态温度场和短时载流量数值计算[J]. 高电压技术, 2011, 37(4): 1002-1007.
Liang Yongchun, Yan Caihong, Zhao Jing, et al. Numerical calculation of transient temperature field and short-time current carrying capacity of cable- laying cable group[J]. High Voltage Engineering, 2011, 37(4): 1002-1007.
[16] 张尧, 周鑫, 牛海清, 等. 单芯电缆热时间常数的理论计算与试验研究[J]. 高电压技术, 2009, 35(11): 2801-2806.
Zhang Yao, Zhou Xin, Niu Haiqing, et al. Theoretical calculation and experimental research on thermal time constant of single-core cables[J]. High Voltage Engineering, 2009, 35(11): 2801-2806.
[17] Ocloń P, Cisek P, Pilarczyk M, et al. Numerical simulation of heat dissipation processes in under- ground power cable system situated in thermal backfill and buried in a multilayered soil[J]. Energy Conversion and Management, 2015, 95: 352-370.
[18] 吕安强, 寇欣, 尹成群, 等. 三芯海底电缆中复合光纤与导体温度关系建模[J]. 电工技术学报, 2016, 31(18): 59-65.
Lü Anqiang, Kou Xin, Yin Chengqun, et al. Modeling of the relationship between composite fiber and conductor temperature in a three-core submarine cable[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 59-65.
[19] Lü Anqiang, Li Jing. On-line monitoring system of 35kV 3-core submarine power cable based onj-OTDR[J]. Sensors & Actuators A Physical, 2018, 273: 134-139.
Finite Element Analysis for the Influence of Clamp on the Thermal Characteristics of High Voltage Insulated Power Cable
1,23415
(1. Department of Electronic and Communication Engineering North China Electric Power University Baoding 071003 China 2. Hebei Key Laboratory of Power Internet of Things Technology North China Electric Power University Baoding 071003 China 3. Department of Computer North China Electric Power University Baoding 071003 China 4. China Electric Power Research Institute Wuhan 430074 China 5. State Grid Zhoushan Electric Power Supply Company of Zhejiang Power Corporation Zhoushan 316021 China)
The clamp is an essential component of the installed high-voltage insulated cable. In order to obtain the influence of clamp on the thermal characteristics of the cable, the electrothermic coupling finite element analysis is carried out on a typical 220kV AC single core XLPE insulated cable. According to the actual situation of cable laying in a certain city in China, the two dimensional and three dimensional electrothermal coupling finite element models of the cable under five different material clamps are established. The ampacity ratings and thermal time constants of the cable under different clamps are obtained through steady-state and transient thermodynamic calculation. The distribution law of conductor temperature in radial and axial directions is obtained by calculating the cable temperature under different clamp materials and intervals, and the relation function of the clamp material and interval with the cable conductor temperature is obtained. The results show that the material and interval of the clamps have an effect on the cable's ampacity ratings and thermal time constant. There is a critical value for the thermal conductivity and interval of the clamp, and the conductor temperature on both sides of this value varies greatly. This paper can provide theoretical and data support for cable construction and operation.
Clamp, high voltage cable, ampacity ratings, thermal time constant, finite element
10.19595/j.cnki.1000-6753.tces.201003
TM247; TN818
国家自然科学基金重点项目(61775057, 51407074)和河北省自然科学基金重点项目(E2015502053)资助。
2020-08-07
2020-11-12
吕安强 男,1979年生,博士,副教授,研究方向为分布式光纤传感及智能电网状态监测。E-mail: lvaqdz@163.com
李 静 女,1979年生,硕士,讲师,研究方向为电力系统有限元建模和信号与信息处理。E-mail: lijing791119@163.com(通信作者)
(编辑 陈诚)

