面向微型能源互联网接入的交直流配电网协同优化调度策略
郑 重 苗世洪 李 超 张 迪 韩 佶
面向微型能源互联网接入的交直流配电网协同优化调度策略
郑 重1,2苗世洪1,2李 超1,2张 迪1,2韩 佶1,2
(1. 华中科技大学电气与电子工程学院强电磁工程与新技术国家重点实验室 武汉 430074 2. 华中科技大学电力安全与高效湖北省重点实验室 武汉 430074)
分布式电源通过微型能源互联网(简称微能网)的方式接入配电网可以充分发挥微能网多能耦合互补的特点,促进可再生能源消纳。该文充分考虑交直流配电网和微能网的技术优势及交互影响,研究了计及动态网络重构和多能源协同的交直流配电网优化调度策略。首先,根据含微能网的交直流配电网系统结构和调度模型特点,研究以配电网节点边际电价和微能网购/售电功率为交互变量的协调运行机制;其次,以交直流配电网和微能网运行成本最低为目标,充分考虑网络运行约束和网络间交互耦合约束,建立交直流配电网协调调度模型;再次,在混合整数二阶锥规划模型的节点边际电价推导基础上,提出基于极限学习机耦合交互的模型快速求解方法;最后,在含微能网的改进IEEE 33节点交直流配电网开展了算例分析。仿真结果表明,所提调度架构能充分降低网络运行成本,促进微能网和交直流配电网间信息交互,同时该文所提求解技术能够在确保计算精度的前提下极大地提高求解效率。
交直流配电网 微型能源互联网 协同优化调度 动态网络重构 极限学习机
0 引言
大力发展清洁能源已经成为世界各国应对环境污染和资源枯竭等问题的重要战略共识[1-2]。随着清洁能源大规模以分布式电源(Distributed Generation, DG)的方式接入配电网,配电网的潮流分布发生了深刻变化,传统的配电网调度模式已经无法满足系统的运行需求[3]。交直流配电网由于具有拓扑结构灵活、潮流可控等优势,成为未来智能配电网的一个重要发展趋势[4-7]。与此同时,由于清洁能源具有随机性、间歇性等特性,清洁能源的大量无序接入为电网安全稳定运行带来了严峻挑战,冷-热-电-气深度耦合的微型能源互联网(简称微能网)的发展与应用为上述问题的解决提供了新的思路[8-11]。因此,如何充分发挥交直流配电网灵活拓扑重构和微能网多能耦合替代的优势,并实现二者的协同优化,已经成为进一步促进清洁能源高效消纳的关键问题之一。
在能源互联网发展背景下,含多能微电网接入的交直流配电网协同优化相关研究近年来渐渐兴起。传统文献建模思路大致可以分为集中式和分布式两大类。针对集中式建模方法,文献[12-13]对冷热电联供型多微网系统的优化配置模型开展研究,同时计及多主体利益关系制定系统最优配置方案,但微电网与微电网间、微电网与配电网间的协同交互作用未能得到充分考虑。针对该问题,文献[14]建立考虑微电网间功率交互和微源出力协调的优化调度模型,该模型既考虑了微电网与配电网、微电网与微电网之间的功率交互,也考虑了微电网之间的功率交互对微电网内部制冷或制热的微源出力的影响,但其本质仍是微电网间的相互影响分析,外接配电网等效为根据分时电价购售电的电能供应商。上述文献利用集中式算法进行统一建模计算,普遍存在迭代次数多、计算复杂、收敛性无法保证等显著缺陷。鉴于此,相关学者进一步提出了分布式建模方法。对于交直流配电网而言,其接入的微能网可类比为微电网,微能网和所接配电网间的协调机制也可以参考配电网和微电网间的协调机制。然而,微能网和配电网的协调关系中,配电网电价会直接影响到微能网中的运行成本和能源生产方案,从而影响微能网对配电网的购售电功率。由此可见,不同于常见配电网与微电网之间交互边界功率的同构协调机制,此时的协调变量是异构的。为了解决这类问题,相关学者提出了异构分解法[15-16],为不同系统之间的协同优化提供了一定基础。针对多主体间信息私密性较差,通信需求较高等问题,文献[17-19]将冷热电联供型多微网和主动配电网作为两个不同的利益主体,采用分布式建模方法,建立考虑电能交互的冷热电联供型多微网系统优化调度模型。文献[20]提出了含综合能源联供型微网的配电网日前鲁棒优化调度模型,但其综合能源微网模型中没有考虑到综合能源用户参与,且模型需要进行多次迭代计算,计算效率较低。文献[21-22]也从含微能网配电网协调调度和扩展规划的角度展开了相关研究,但是优化模型中配电网调度资源较为有限。
综上所述,现有微能网与配电网协同优化模型研究中大多未能充分考虑配电网与微能网间的交互耦合,且未充分挖掘交直流配电网动态网络重构和微能网用户需求响应等灵活调度资源,无法充分发挥配电网和微能网协调调度对可再生能源消纳的促进作用;此外,现有协调调度求解算法普遍存在计算复杂、耗时较长等缺陷,工程应用价值有限。
针对上述问题,本文充分考虑交直流配电网与微能网的交互影响,研究计及动态网络重构和多能源协同的交直流配电网优化调度策略。首先,根据含微能网的交直流配电网系统结构和调度模型特点,以配电网节点边际电价和微能网购/售电功率为交互变量,结合异构分解技术构建了交直流配电网-微能网协调调度框架,进而以系统经济性最优为目标,建立了交直流配电网协调调度模型;然后,通过二阶锥约束等价变形和整数松弛定价,完成了混合整数二阶锥规划模型节点边际电价的数学推导,并提出了一种基于极限学习机(Extreme Learning Machine, ELM)耦合交互的模型快速求解方法;最后,在含微能网的改进IEEE 33节点交直流配电网验证本文所提模型的有效性和求解技术的高效性。
1 交直流配电网-微能网协调调度框架与建模
1.1 交直流配电网-微能网协调调度框架
对于交直流配电网而言,微能网接入后,相当于一个广义负荷,需要重点关注微能网接入节点的边界功率对系统安全经济运行的影响;对于微能网而言,交直流配电网的电能售价会影响微能网的系统运行收益和能源生产方案,不同的电能售价也会导致微能网对交直流配电网有不同的购/售电需求。可见,微能网和交直流配电网之间将会通过边界信息相互影响,实现交直流配电网和微能网的协调调度具有重要意义。本文提出了一种交直流配电网-微能网协调调度框架,其结构图如图1所示。

图1 交直流配电网-微能网协调调度框架
该协调调度框架包括交直流配电网和微能网内部优化过程以及优化模型之间的耦合过程,具体介绍如下:
1)交直流配电网和微能网的内部优化
交直流配电网的内部优化模型以系统运行成本最低为目标,协调调度全网可控开关状态、可控分布式发电(Distributed Generation, DG)出力、电压源换流器(Voltage Source Converter, VSC)调制比、静止无功补偿装置(Static Var Compensator, SVC)补偿电位等调度资源,实现系统的安全经济运行;微能网的内部优化模型以系统能源生产成本最低为目标,根据系统外部电价制定系统内部能源售价和能源生产方案。交直流配电网和微能网的内部优化模型的一般表达形式详见链接(https://pan.baidu. com/s/1-ZNtYd98QThNeqZMQ4s_0w,提取码:1111,后文简称链接)。
2)交直流配电网和微能网优化耦合模型
本文采用极限学习机实现交直流配电网和微能网优化模型之间的耦合,该过程如图2所示。对于交直流配电网优化模型而言,将各个微能网购/售电功率作为极限学习机的输入变量,将配电网的节点边际电价作为极限学习机的输出变量;对于微能网优化模型而言,将节点边际电价作为极限学习机的输入变量,将各个微能网购、售电功率作为极限学习机的输出变量。本文将在2.3节对两个优化模型的耦合模型进行详细说明。
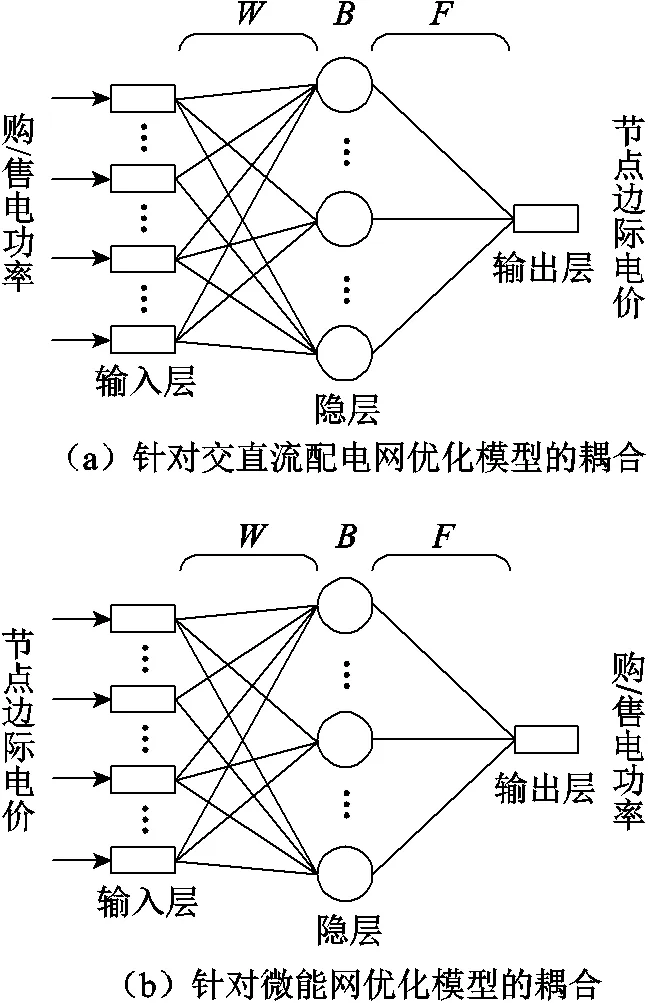
图2 交直流配电网和微能网优化模型的耦合架构
1.2 上层交直流配电网优化调度模型
1.2.1 上层目标函数
上层交直流配电网优化调度模型的目标函数为
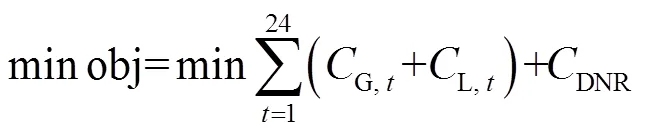
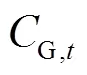
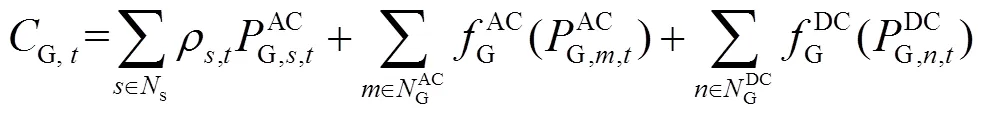

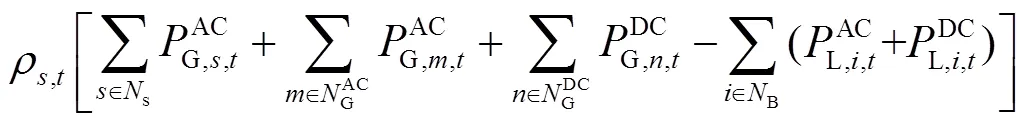

1.2.2 上层约束条件
1)潮流方程约束
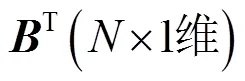
考虑动态网络重构和静止无功补偿器接入后的潮流方程约束为
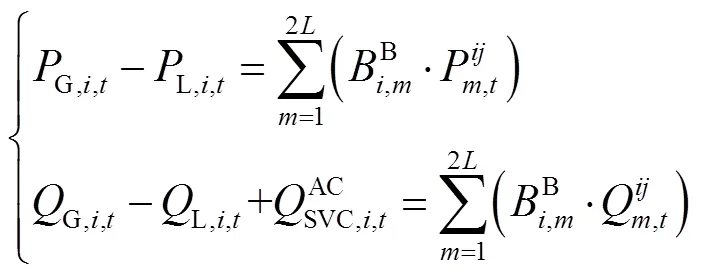

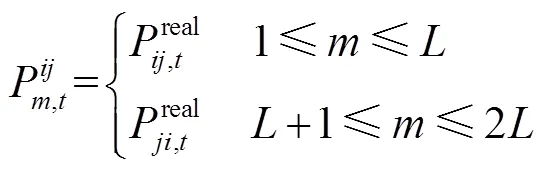
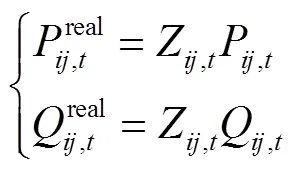
2)网络安全运行约束
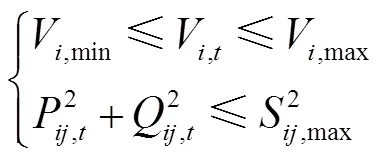
3)换流站容量约束
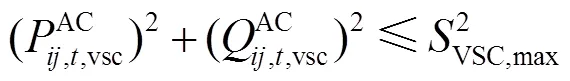
4)无功调节装置约束
由于DG接入,交直流配电网中潮流可能出现反向,导致某些母线出现过电压问题,因此本文考虑交直流配电网中存在以静止无功补偿装置为代表的无功调节装置,静止无功补偿装置的无功调节功率需要满足范围约束,即
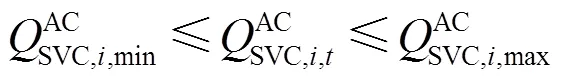
5)电源出力约束
变电站传输功率、交流电网电源和直流电网电源的有功无功出力需要满足出力上、下限约束,即
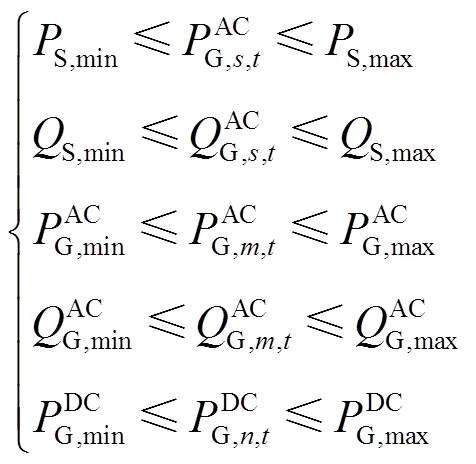
1.3 下层微能网优化调度模型
微能网系统运行商需要根据配电网电价制定系统内部能源生产方案,同时调整系统内部电价,激励微能网中的综合能源用户通过用能替代效应积极参与系统优化。因此,本文以微能网生产成本最低为目标,在满足供需双侧安全运行相关约束条件下构建微能网优化调度模型。
1.3.1 下层目标函数
接入交直流配电网后,微能网面临变化的电价,且被允许在满足安全约束的条件下向配电网倒送功率,目标函数为
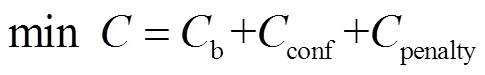
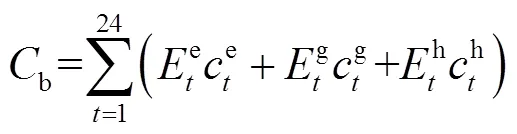
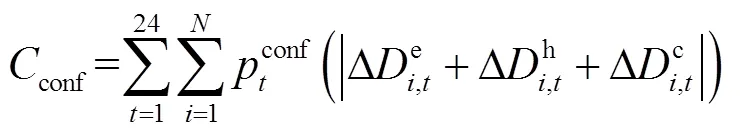
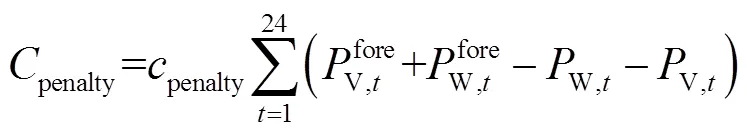
1.3.2 下层约束条件
微能网约束条件可以分为能源供给侧约束和能源需求侧约束。
1)能源供给侧约束
(1)能源平衡约束
系统运营商向上级能源网络购买电力、天然气、热力能源资源,通过系统各类能源转换设备向多能用户供能,各类能源平衡约束为


(2)设备运行参数约束
主要考虑到各类能源转换设备的容量限制,各设备的运行约束为
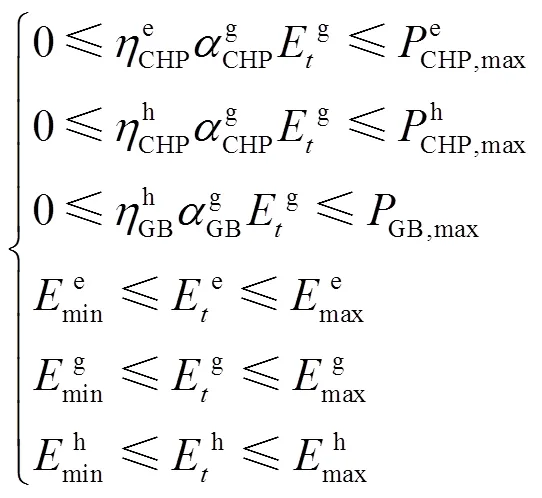
(3)能源价格变化范围约束
系统运营商可以制定向用户出售电能和热能的价格,为了保证系统运营商的运行收益又不造成用户用能成本过高,需要对能源价格变化范围进行限定,即

(4)风光出力约束
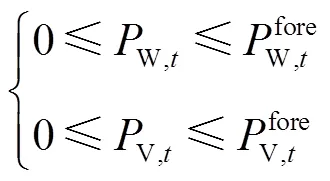
2)能源需求侧约束
需求侧采用考虑用户需求耦合响应特性的综合需求响应模型。在此模型中,认定用户有一个初始冷/热/电需求;采用电价弹性矩阵模型描述用户电负荷响应过程,同时考虑需求之间的耦合响应,假设用户受电负荷影响的相关需求转由热负荷设备供给。由此建立相关约束如下。
(1)需求平衡约束
用户需求可以分为原始用能需求和需求偏移量两个部分,如式(21)所示。其中,原始用能需求见式(22),需求偏移量根据响应情况可由式(23)表示。
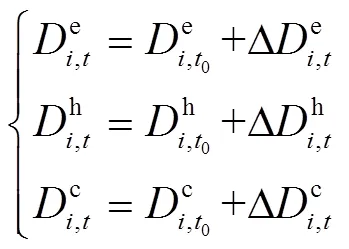
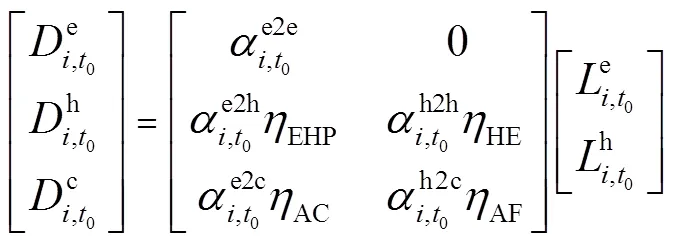

(2)响应量大小约束
在用户自由分配负荷变化量时,需要保证各类需求对应负荷变化量在总负荷响应范围内,表达式为
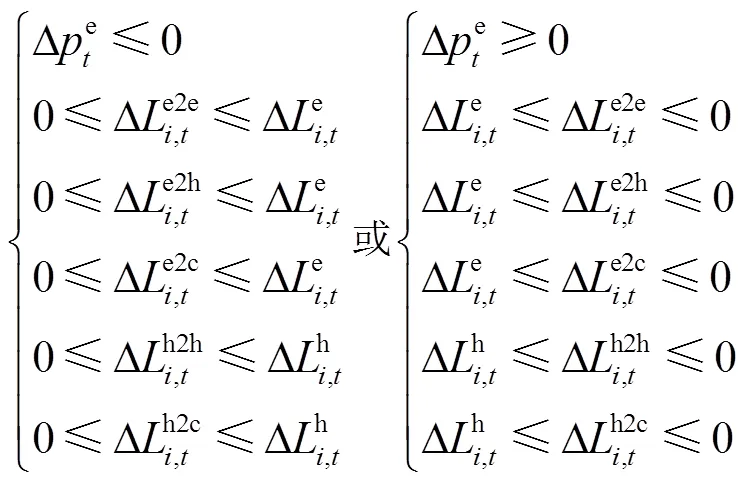
(3)用能成本约束
当用户响应电价变化时,电、热负荷变化将会改变用户的用能成本。为避免用户利益过度受损,需要考虑用能成本约束,即
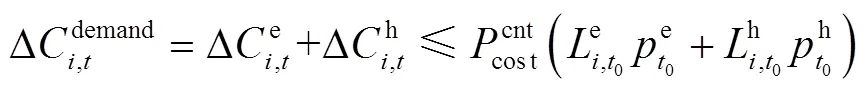
2 基于ELM耦合交互的模型求解方法
本文将交直流配电网的节点边际电价和微能网的购、售电功率作为交互变量,在异构分解框架中,利用极限学习机强大的非线性映射和泛化能力,实现两交互变量的耦合,以提高调度模型的求解效率。下面首先介绍模型求解中的重要概念及计算工具——节点边际电价和极限学习机;并在此基础上,介绍交直流配电网和微能网的极限学习机耦合模型,给出模型快速求解的流程。
2.1 节点边际电价
节点边际电价以每个节点向用户供电的边际成本确定节点电价,通过向用户提供经济信号,利用节点边际电价能够科学衡量能量价值,充分促进市场合理竞争[24]。一般地,节点边际电价是以最优潮流模型为基础进行推导的,但是本文提出的交直流配电网优化调度模型是一个混合整数二阶锥规划问题,其节点边际电价的推导主要面临两个难题:
1)传统方法推导出的二阶锥约束的互补松弛条件将为二次等式,节点边际电价也将以二次形式存在,无法利用成熟的规划方法获取。因此,为了对节点边际电价进行线性化表示,必须对二阶锥约束的互补松弛条件形式等价变形,进而确定二阶锥约束的拉格朗日乘子。
2)传统的节点边际电价推导模型是以连续模型为基础进行推导的,但本文模型是一个混合整数规划问题,其节点边际电价会受到整数变量的影响,传统的推导方式将不再适用[25]。
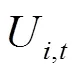
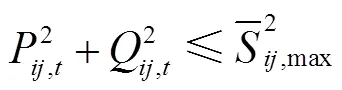
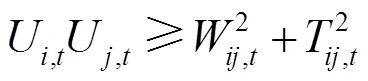
其二阶锥标准表达形式为
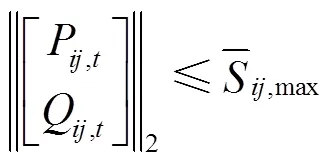
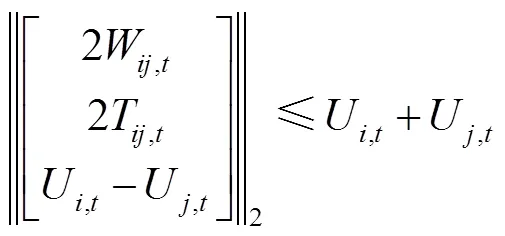
式(29)和式(30)两个约束的互补松弛条件需要匹配于相应的拉格朗日乘子,即式(29)和式(30)两个二阶锥的互补松弛条件形式如式(31)和式(32)所示。
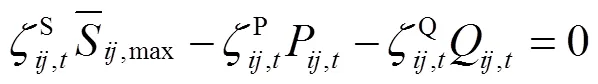
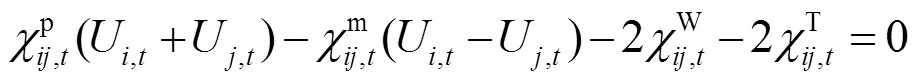
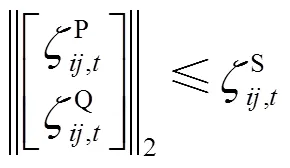

在不考虑整数变量的情况下,本文提出的交直流混合配电网联合优化调度模型是一个连续凸优化模型,其拉格朗日形式为

式中,G为交直流配电网电源集合。
根据稳定性条件可得
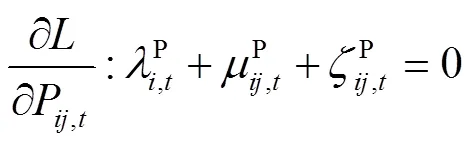

将式(31)和式(32)代入式(36)和式(37)可得
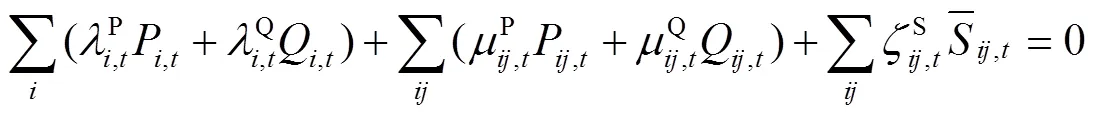
式(38)为该系统的预算平衡式。式中第一项加和代表电力系统生产费用,第三项加和代表为系统拥塞所产生的费用,第二项加和则代表网损和电压降产生的费用。
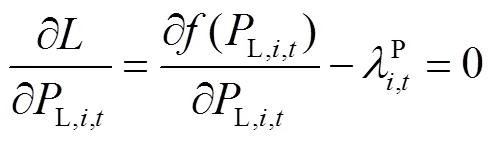
前述模型是对连续模型的节点边际电价进行求解。对于混合整数规划问题,可以采用整数松弛定价的思路[26]。本文借鉴这一思路,先对原交直流混合配电网联合优化调度模型进行整体优化求解,得到整数变量最优值后将其作为参数代入原模型中,进而通过式(27)~式(39)求解松弛后的节点边际电价。
2.2 极限学习机
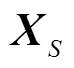
ELM的基本方程为
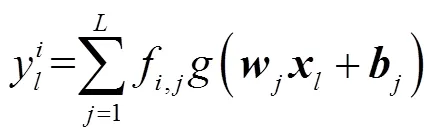
将式(40)写成矩阵形式,即
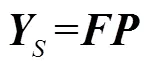
其中


此外,本文采用标准方均根误差[28-29]对ELM拟合误差进行表征,其具体计算公式为
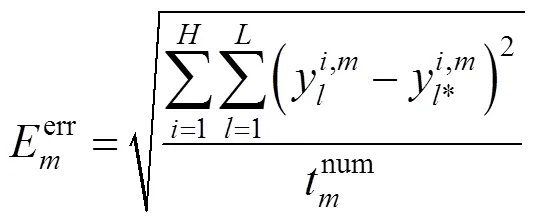
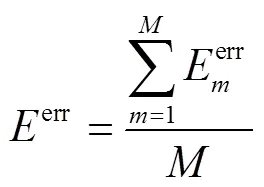
2.3 交直流配电网和微能网优化模型的耦合
对于交直流配电网优化模型而言,各个微能网购售电功率为模型的输入变量,配电网的节点边际电价为模型输出变量。因此交直流配电网优化模型的ELM等效优化模型中输入、输出矩阵分别为
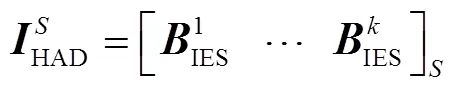
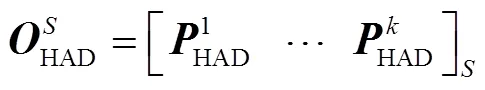
对于微能网优化模型而言,微能网接入节点的节点边际电价为模型输入变量,系统购售电功率为模型输出变量。第个微能网模型的ELM等效优化模型中输入、输出矩阵分别为
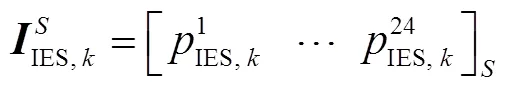
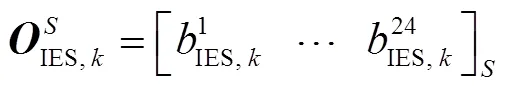
2.4 模型快速求解流程
由图1可知,本文需要分别训练两类ELM。第一类是针对交直流配电网优化模型的耦合,将各个微能网购、售电功率作为ELM的输入变量,将配电网的节点边际电价作为ELM的输出变量;第二类是针对微能网优化模型的耦合,将节点边际电价作为ELM输入变量,将各微能网购、售电功率作为ELM输出变量。两类ELM的输入输出关系详见链接。
由于两类ELM的训练过程完全相同,下面以第一类ELM为例,介绍ELM的训练方法:
(1)随机生成若干组微能网购、售电数据,利用交直流配电网优化调度程序求解节点边际电价,进而将上述数据作为第一类ELM的输入训练数据。
(2)确定隐层节点总数,选择激励函数(⋅)。
(3)随机初始化输入权值和隐层阈值向量。
(4)根据式(42)计算出隐层输出矩阵。
(5)根据式(43)计算出输出权值矩阵。
在完成上述两类ELM的训练后,将其作为交直流配电网和微能网优化模型的耦合交互工具,完成整个优化模型的快速求解。交直流配电网-微能网协调调度模型求解的流程如图3所示。
算法具体步骤如下:
(1)对交直流配电网和微能网中的优化变量进行随机初始化,初始化迭代次数iter=1。
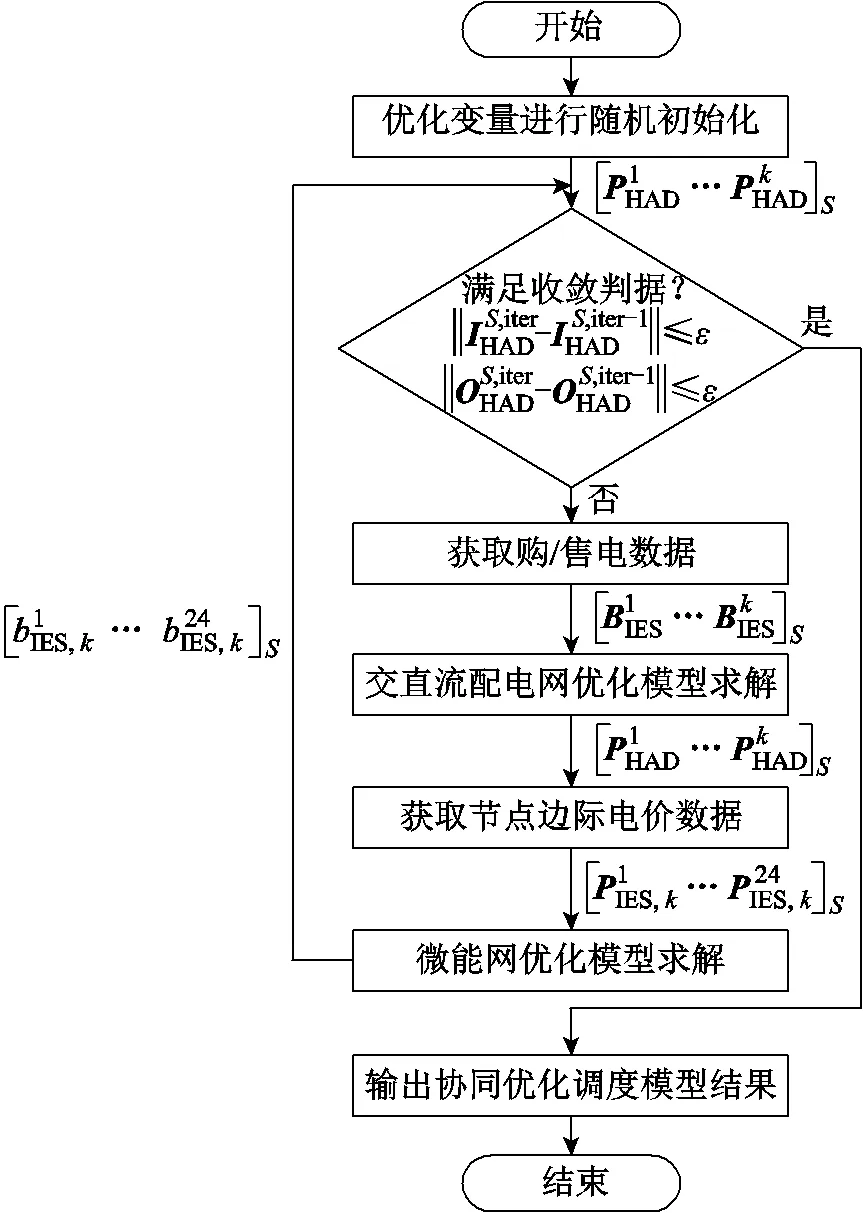
图3 基于ELM的双层模型求解流程
(2)将微能网购、售电数据输入第一类ELM,求解交直流配电网优化模型,获取节点电价。
(3)将电网节点电价数据输入个第二类ELM,依次求解对应个微能网优化模型,获取微能网购、售电数据。
(4)计算第iter次迭代节点边际电价残差及微能网购、售电功率残差,判断是否满足式(50)所示的收敛判据,若满足,输出交直流配电网-微能网协调调度模型优化结果;若不满足,返回步骤(2)。
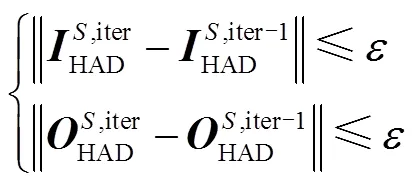
3 算例分析
3.1 算例系统说明
为验证所提计及动态网络重构和多能源协同的交直流配电网优化调度模型的有效性,本文基于一个包含两个微能网的交直流配电系统进行算例分析,算例系统结构如图4所示。所用算例系统中交直流配电网采用改进的IEEE 33节点交直流配电网,微能网1对文献[30]所用多能系统进行改进,微能网2在微能网1的基础上进行改进,使其具备不同的负荷特性、DG出力特性和设备特性。两个微能网分别接于交直流配电网中的交流节点24和交流节点5。
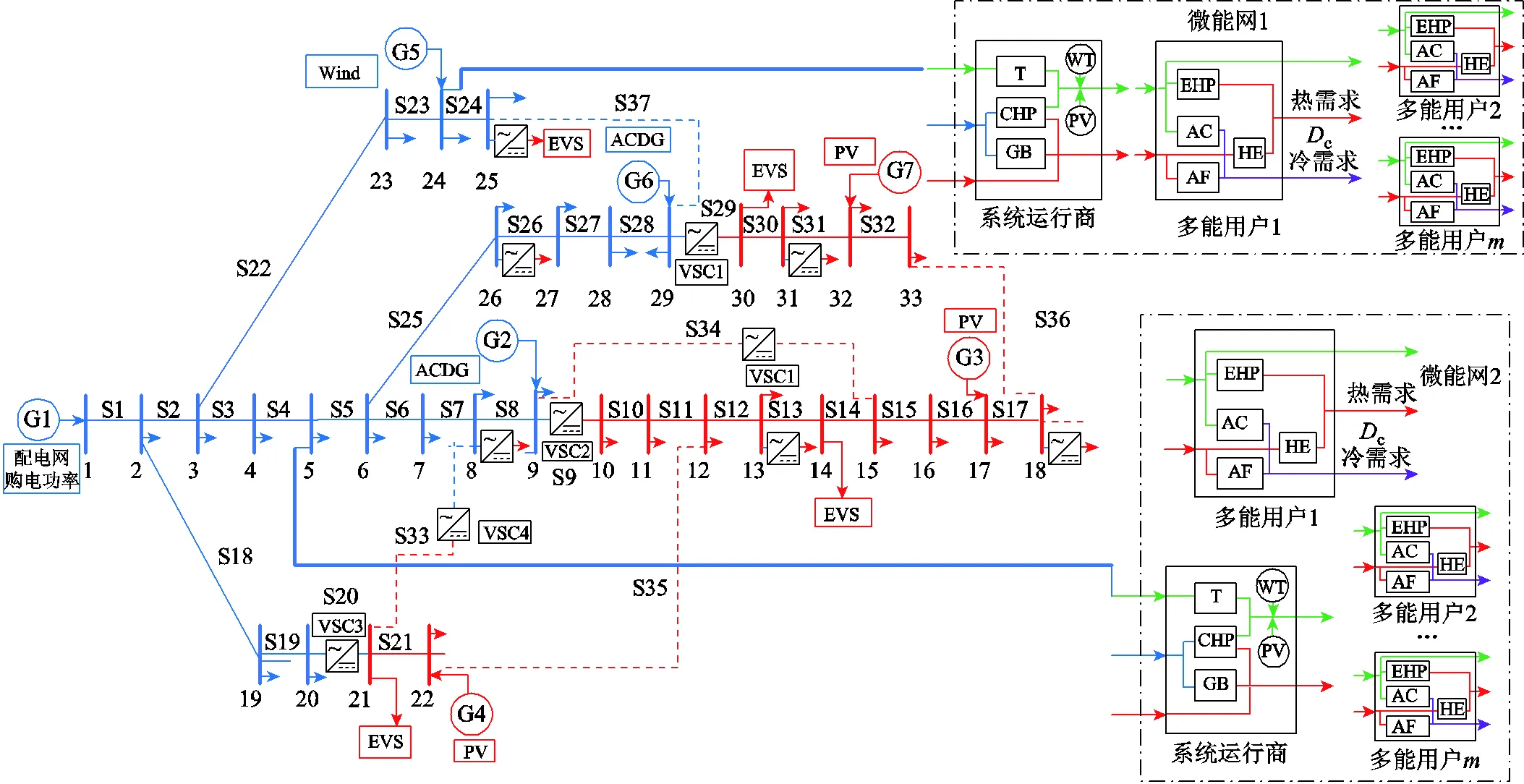
图4 含微能网的交直流配电网结构
3.2 模型参数选取
为了建立足够精度的等效优化模型,需要获得足够多的学习样本。本文在边界变量允许范围内随机设置1 000组变量参数,分别代入两个优化模型中求出相应模型最优时的节点边际电价和最优购售电功率。分别选用100、200、300、400、500、600、700、800和900组数据作为训练样本,分别输入两个ELM模型中进行训练,再用剩余100组数据进行模型准确性测试,其中,ELM拟合误差计算公式详见式(44)和式(45)。不同数量训练数据下ELM的拟合误差见表1。
表1 不同数量训练数据下ELM的拟合误差

Tab.1 Fitting errors of extreme learning machine with different training data
从表1中可以看出,当训练数据为600时,拟合误差趋向于收敛,约为6%。因此,本文选择利用900组训练样本得到的两个ELM模型作为后续优化模型中的耦合工具。
需要说明的是,为了选择合适的ELM核函数,本文分别针对RBF核函数(RBF kernel)、线性核函数(Linear kernel)、多项式核函数(Polynomial kernel)及波核函数(Wave kernel)的拟合误差进行对比分析,利用900组样本进行训练,并利用另外100组数据进行测试,测试结果见表2。
表2 不同核函数下ELM的拟合误差

Tab.2 Fitting errors of extreme learning machine with different kernel functions
由表2可知,采用RBF核函数时,模型的平均标准方均根误差最低,拟合效果最优。因此,本文最终选取RBF核函数进行ELM训练。
3.3 模型求解精度和效率
为了提高求解效率,本文提出了基于ELM的交直流配电网双层协调调度模型,采用ELM算法实现交直流配电网优化模型和微能网优化模型的快速响应,避免每次迭代过程中求解高维子优化问题耗时过长的缺陷,极大地提升了计算效率。本文进一步分析引入ELM对模型求解精度的影响。
首先,本文将未采用ELM的协调调度模型优化结果作为基准值,对比分析采用ELM的优化结果,以验证本文所提模型的精确性。ELM拟合节点边际电价相对误差曲线如图5所示。LMP1和LMP2分别代表两微能网接入节点的节点边际电价。从图5中可以看出,所得到各时段的节点边际电价误差均低于6%。因此,本文基于ELM的交直流配电网优化模型可以通过数据学习的方式建立交互变量与目标函数之间的关系,从而避免了迭代优化中交替进行的优化过程,在允许的误差范围内提高了优化过程的求解效率。
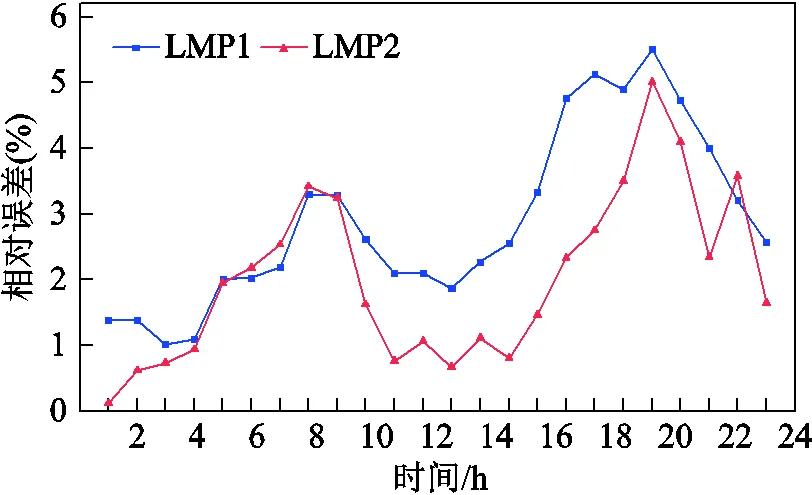
图5 ELM拟合节点边际电价相对误差曲线
为进一步说明本文所提基于ELM耦合交互的模型求解方法在求解精度及计算效率上的优越性,引入传统集中式求解算法及基于异构分解的分布式求解算法[15-16]与本文所提算法进行对比,结果见表3。
表3 模型求解精度及效率对比表
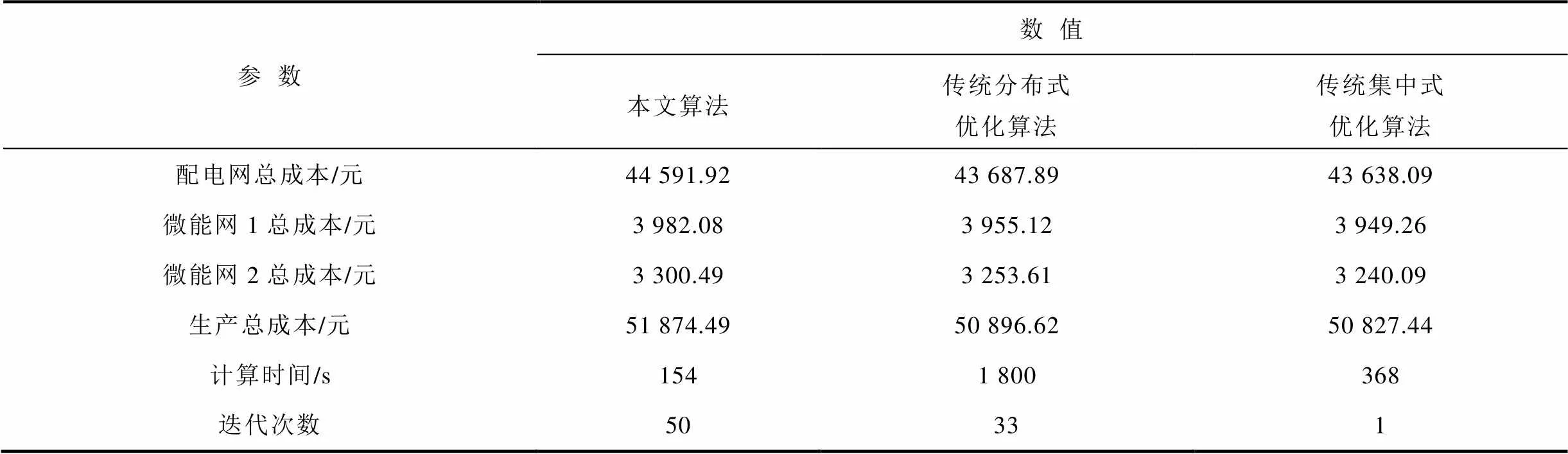
Tab.3 Comparison table of solving efficiency and accuracy
从表3可以看出,本文所提基于ELM耦合交互的模型求解方法的计算精度较高,生产总成本、交直流配电网发电成本及各微能网购能成本误差均保持在3%以内,在工程应用上完全能够接受。与此同时,相较于传统分布式和集中式优化算法,本文所提算法在计算效率层面具有显著优势,整个优化过程在154s内完成。由此可见,基于ELM耦合交互的模型求解方法在允许小范围牺牲最优性的条件下极大地提高了模型的求解效率,既克服了传统分布式优化算法求解子优化问题耗时过长的缺陷,亦避免了传统集中式优化算法在节点数量增加、网络规模扩大时所面临的收敛性问题,为高效求解此类多个主体、调度资源多样、调度模型复杂的协同优化问题提供了坚实基础。
3.4 协调调度和独立调度结果对比
为进一步体现本文所提交直流配电网协调调度模型相较于传统独立调度模型的优势,本文设置如下三种调度方式进行对比分析:
调度方式1(协调调度方式):即本文提出的基于ELM的交直流配电网-微能网协调调度方式,交直流配电网和两个微能网进行协调调度。微能网根据配电网给定电价分别进行自调度,将自身功率需求传递给配电网后,配电网进一步根据两个微能网功率需求进行优化调度,将优化后的配电网节点电价传递给微能网,模型间反复交互迭代直至收敛。
调度方式2(独立调度方式-1):交直流配电网和两个微能网进行独立调度。两个微能网根据交直流配电网给定节点电价进行自调度,并向配电网上传24h功率需求,配电网根据微能网功率需求进行配电网优化。两个微能网接入节点的电价统一参考河北南部电网1~10kV配电网峰谷销售电价。
调度方式3(独立调度方式-2):该调度方式与调度方式2基本相同,唯一的区别之处在于调度方式3中微能网的优化目标调整为向交直流配电网购电功率最少(或者售电功率最多),以分析微能网向交直流配电网提供最小功率需求(或者最大功率支撑)时全系统的运行生产总成本。
需要说明的是,为验证本文协调调度模型及求解算法在计及多微能网接入的交直流配电网系统中的有效性和优越性,本文进一步增加了计及三微能网接入的交直流配电网系统算例分析,详见链接。此外,由于采用的交直流配电网系统和微能网系统参数不同,涉及金额单位的问题,因此本文在迭代优化过程中将美元电价按1:7的汇率转换为人民币进行,这并不会影响到最终调度结果。
1)生产成本优化结果
交直流配电网和微能网的生产成本优化结果见表4。
表4 三种调度方式下交直流配电网和微能网生产成本优化结果
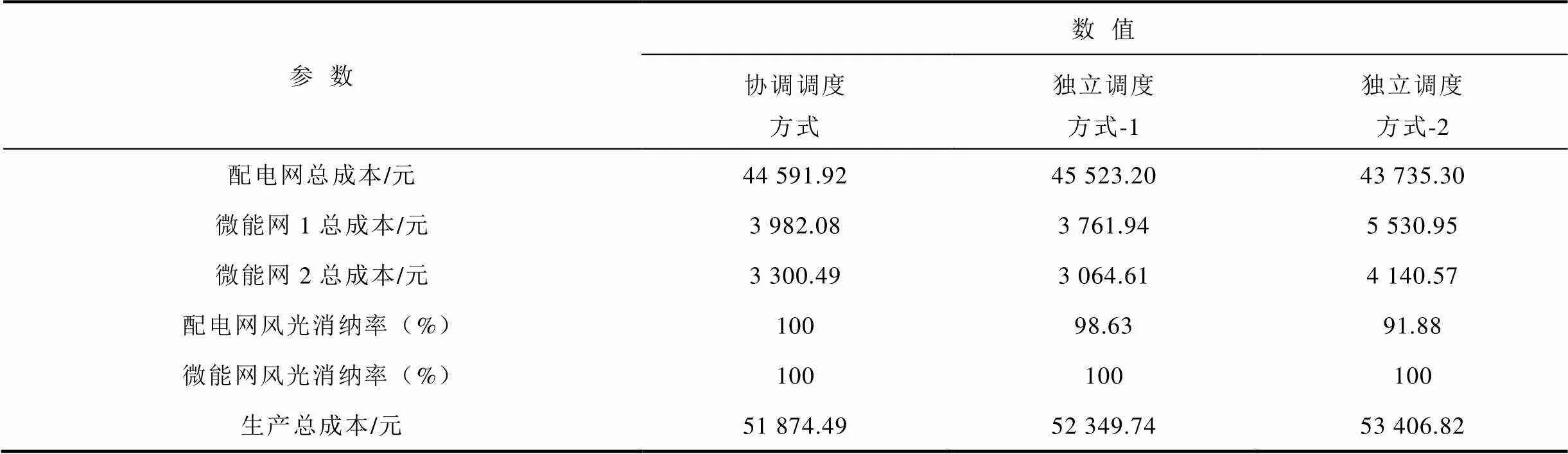
Tab.4 The cost of AC-DC distribution network and micro-energy-internet under 3 dispatching modes
分析表4中数据可看出:
(1)独立调度方式-1下的微能网购能成本最低,发电成本最高,独立调度方式2下的微能网购能成本最高,发电成本最低;协调调度方式下的微能网购能成本和配电网发电成本介于两者之间。这主要是由于在独立调度方式-1下微能网的调度方式为自调度,其以微能网自身的运行成本最小为目标,所以牺牲了部分交直流配电网的运行经济性,以确保微能网运行最优;而独立调度方式-2则恰好相反,其以向交直流配电网提供最大功率支撑(或者最小功率需求)为目标,旨在充分发挥微能网的多能耦合替代特性,使得微能网内部资源利用最大化,所以该调度方式下微能网的购能成本最高、交直流配电网的发电成本最低;而协调调度方式则综合考虑了微能网和交直流配电网的运行经济性。
(2)协调调度方式下的生产总成本最低,其次是独立调度方式-1,独立调度方式-2下的生产总成本最高,协调调度方式下生产总成本相比独立调度方式最高相差1532.33元/天。相较于独立调度方式,协调调度方式能够可观地降低系统总生产成本。
(3)相较于协同调度方式所能够实现配电网风光全额消纳,两种独立调度方式中配电网均出现了不同程度的弃风弃光问题。这主要是由于两种独立调度方式中配电网与微能网间缺乏有效数据信息交互,配电网及微能网在优化过程中仅考虑自身经济性,系统整体资源协同利用效率较为有限;此外,独立调度方式-2以向交直流配电网购电功率最少为优化目标,该优化目标将导致配电网弃风弃光现象进一步加剧。同时,本文所提算法能够通过节点边际电价与微能网购售电功率的迭代交互获取全局最优能源生产方案,进而有效地促进清洁能源消纳。
2)交直流配电网优化调度结果
三种调度方式下,交直流配电网负荷曲线及电源出力情况如图6所示。

图6 三种调度方式下交直流配电网负荷及电源出力曲线
分析图6中信息可以看出,协调调度方式下两个微能网的购售电方案相对更为合理,对交直流配电网起到了一定的削峰填谷的作用。当交直流配电网位于负荷高峰期时,两个微能网向配电网售电,反之则微能网向配电网购电,缓解了配电网调峰压力,避免了配电网电源出力的频繁调节。而两种独立调度方式下微能网由于缺乏与交直流配电网的有效交互机制,其能源生产方案与交直流配电网的实际需求并不匹配,常常会出现负荷低谷期微能网向配电网售电或者是负荷高峰期微能网向配电网购电的现象。因此,从系统层面而言,协调调度方式更有利于发挥不同调度资源的协调互补特性,优化系统的能源利用方式。
3)微能网优化调度结果
三种调度方式下,微能网1和微能网2内部的电能生产方案如图7所示。

分析图7可以发现:无论是协调调度方式还是两种独立调度方式,微能网接入交直流配电网后,由于微能网可以向交直流配电网倒送功率,所以当单独考虑微能网调度时出现的弃风光现象将不再出现;另外,由于微能网2内部的风光资源更加充足,因此微能网2向交直流配电网的售电积极性更高,这也说明微能网是促进风光资源消纳的有效手段之一。进一步纵向对比图7中的相关数据可知,协调调度方式下微能网内部的负荷需求响应趋势与配电网负荷峰谷分布几乎相反,即在配电网负荷高峰期时微能网负荷下降,在配电网负荷低谷期时微能网负荷上升,而两种独立调度方式下的负荷需求响应则无明显特征,说明协调调度方式更有利于发挥微能网的负荷需求响应特性,平滑配电网负荷曲线。
三种调度方式下,微能网1和微能网2内部的电能生产方案见链接,可以发现,协调调度方式对微能网内部的热能生产方案具有较大的影响,其本质是由于用户综合需求响应的影响:不同调度方式下微能网的优化目标不同,对应不同的响应电价,电价将对用户的热负荷需求产生较大影响,进而影响了微能网内部的热能生产方案。与此同时,独立调度方式-2下微能网热负荷仅由CHP机组和储热装置供应,而协调调度方式和独立调度方式-1下均有电热泵参与热负荷供应,且三种调度方式下均无燃气锅炉参与。这主要是由于CHP机组具有热电联产的独特优势,当微能网接入配电网后可以将其内部盈余的风电、光伏甚至是气电倒送至交直流配电网中,使得CHP机组的优势被进一步扩大,热电联产的效益远远高于燃气锅炉以气产热的效益,所以三种调度方式下燃气锅炉都没有被安排热负荷供应计划。另一方面,协调调度方式和独立调度方式-1电热泵承担热负荷的时刻均为轻电重热负荷阶段,此时的节点电价一般也相对较低,所以通过电热泵将电负荷转换成热负荷具备经济性,而独立调度方式-2的优化目标为向交直流配电网供给最大功率,所以调度计划会避免出现电转气的现象,因此独立调度方式-2没有电热泵参与热负荷供应。
综上所述,本文所提出的协调调度模型可以充分发挥不同调度资源的协调互补特性,促进微能网和交直流配电网之间的信息交互,降低社会生产的总成本。
4 结论
为充分发挥交直流配电网和微能网的协调互补特性,本文对计及动态网络重构和多能源协同的交直流配电网优化调度技术开展研究,提出了基于ELM的交直流配电网协同优化调度模型快速求解方法,通过仿真算例对模型进行了验证,结果表明:
1)本文提出了一种含微能网的交直流配电网协调运行框架,该框架能够反映微能网和交直流配电网之间的影响机理,以节点边际电价和购售电功率为交互变量的协调机制能够有效地实现信息交互。
2)本文提出了一种基于ELM的交直流配电网双层协调调度模型求解方法,该求解方法能够在保证求解最优性的前提下,缩短每次迭代计算时间,实现交直流配电网协同优化模型的快速求解。
3)交直流配电网和接入的微能网之间的协调调度,对于提升系统整体经济性,促进可再生能源消纳和能源清洁化转型具有重要意义。
[1] 国家能源局. 能源发展“十三五”规划[EB/OL]. http://www.nea.gov.cn/135989417_14846217874961n.pdf.
[2] 国家发展和改革委员会, 国家能源局. 能源生产和消费革命战略(2016-2030)[EB/OL]. https://www. ndrc.gov.cn/fggz/zcssfz/zcgh/201704/W020190910670685518802.pdf.
[3] 马钊, 周孝信, 尚宇炜, 等. 未来配电系统形态及发展趋势[J]. 中国电机工程学报, 2015, 35(6): 1289-1298.
Ma Zhao, Zhou Xiaoxin, Shang Yuwei, et al. Form and development trend of future distribution system[J]. Proceedings of the CSEE, 2015, 35(6): 1289-1298.
[4] 黄堃, 刘之涵, 付明, 等. 计及电压风险感知的交直流配电网优化调度[J]. 电力系统自动化, 2021, 45(15): 45-54.
Huang Kun, Liu Zhihan, Fu Ming, et al. Optimal dispatch of AC/DC distribution network considering voltage risk perception[J]. Automation of Electric Power Systems, 2021, 45(15): 45-54.
[5] 曾梦隆, 韦钢, 朱兰, 等. 交直流配电网中电动汽车充换储一体站规划[J]. 电力系统自动化, 2021, 45(18): 52-60.
Zeng Menglong, Wei Gang, Zhu Lan, et al. Planning of electric vehicle charging-swapping-storage integrated station in AC/DC distribution network[J]. Automation of Electric Power Systems, 2021, 45(18): 52-60.
[6] 孙峰洲, 刘海涛, 陈庆, 等. 考虑新能源波动区间的交直流配电网下垂斜率鲁棒优化方法[J]. 电力系统自动化, 2020, 44(14): 62-70.
Sun Fengzhou, Liu Haitao, Chen Qing, et al. Robust optimization method for droop slopes in AC/DC distribution network considering fluctuation interval of renewable energy source[J]. Automation of Electric Power Systems, 2020, 44(14): 62-70.
[7] 李幸芝, 韩蓓, 李国杰, 等. 考虑非高斯耦合不确定性的交直流配电网两阶段概率状态估计[J]. 电工技术学报, 2020, 35(23): 4949-4960.
Li Xingzhi, Han Bei, Li Guojie, et al. Two-stage probabilistic state estimation for AC/DC distribution network considering non-Gaussian coupling uncertainties[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4949-4960.
[8] 刁涵彬, 李培强, 王继飞, 等. 考虑电/热储能互补协调的综合能源系统优化调度[J]. 电工技术学报, 2020, 35(21): 4532-4543.
Diao Hanbin, Li Peiqiang, Wang Jifei, et al. Optimal dispatch of integrated energy system considering complementary coordination of electric/thermal energy storage[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4532-4543.
[9] 陈柏翰, 冯伟, 孙凯, 等. 冷热电联供系统多元储能及孤岛运行优化调度方法[J]. 电工技术学报, 2019, 34(15): 3231-3243.
Chen Bohan, Feng Wei, Sun Kai, et al. Multi-energy storage system and islanded optimal dispatch method of CCHP[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3231-3243.
[10] 尹斌鑫, 苗世洪, 李姚旺, 等. 先进绝热压缩空气储能在综合能源系统中的经济性分析方法[J]. 电工技术学报, 2020, 35(19): 4062-4075.
Yin Binxin, Miao Shihong, Li Yaowang, et al. Study on the economic analysis method of advanced adiabatic compressed air energy storage in integrated energy system[J] Transactions of China Electrotechnical Society, 2020, 35(19): 4062-4075.
[11] 杨经纬, 张宁, 王毅, 等. 面向可再生能源消纳的多能源系统: 述评与展望[J]. 电力系统自动化, 2018, 42(4): 11-24.
Yang Jingwei, Zhang Ning, Wang Yi, et al. Multi-energy system towards renewable energy accommodation: review and prospect[J]. Automation of Electric Power Systems, 2018, 42(4): 11-24.
[12] 林顺富, 刘持涛, 李东东, 等. 考虑电能交互的冷热电区域多微网系统双层多场景协同优化配置[J]. 中国电机工程学报, 2020, 40(5): 1409-1421.
Lin Shunfu, Liu Jitao, Li Dongdong, et al. Bi-level multiple scenarios collaborative optimization configuration of CCHP regional multi-microgrid system considering power interaction among microgrids[J]. Proceedings of the CSEE, 2020, 40(5): 1409-1421.
[13] 李鹏, 吴迪凡, 李雨薇, 等. 基于谈判博弈的多微网综合能源系统多目标联合优化配置[J]. 电网技术, 2020, 44(10): 3680-3690.
Li Peng, Wu Difan, Li Yuwei, et al. Multi-objective union optimal configuration strategy for multi-microgrid integrated energy system considering bargaining games[J]. Power System Technology, 2020, 44(10): 3680-3690.
[14] 王守相, 吴志佳, 庄剑. 考虑微网间功率交互和微源出力协调的冷热电联供型区域多微网优化调度模型[J]. 中国电机工程学报, 2017, 37(24): 7185-7194, 7432.
Wang Shouxiang, Wu Zhijia, Zhuang Jian. Optimal dispatching model of CCHP type regional multi-microgrids considering interactive power exchange among microgrids and output coordination among micro-sources[J]. Proceedings of the CSEE, 2017, 37(24): 7185-7194, 7432.
[15] Li Zhengshuo, Guo Qinglai, Sun Hongbin, et al. Coordinated economic dispatch of coupled transmission and distribution systems using heterogeneous decomposition[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4817-4830.
[16] Li Zhengshuo, Guo Qinglai, Sun Hongbin, et al. A new LMP-sensitivity-based heterogeneous decomposition for transmission and distribution coordinated economic dispatch[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 931-941.
[17] 徐青山, 李淋, 盛业宏, 等. 冷热电联供型多微网主动配电系统日前优化经济调度[J]. 电网技术, 2018, 42(6): 1726-1735.
Xu Qingshan, Li Lin, Sheng Yehong, et al. Day-ahead optimized economic dispatch of active distribution power system with combined cooling heating and power-based microgrids[J]. Power System Technology, 2018, 42(6): 1726-1735.
[18] Xu Qingshan, Li Lin, Xi Chen, et al. Optimal economic dispatch of combined cooling, heating and power-type multi-microgrids considering interaction power among microgrids[J]. IET Smart Grid, 2019, 2(3): 391-398.
[19] 徐青山, 李淋, 蔡霁霖, 等. 考虑电能交互的冷热电多微网系统日前优化经济调度[J]. 电力系统自动化, 2018, 42(21): 36-44.
Xu Qingshan, Li Lin, Cai Jilin, et al. Day-ahead optimized economic dispatch of CCHP multi-microgrid system considering power interaction among microgrids[J]. Automation of Electric Power Systems, 2018, 42(21): 36-44.
[20] 周丹, 孙可, 张全明, 等. 含多个综合能源联供型微网的配电网日前鲁棒优化调度[J]. 中国电机工程学报, 2020, 40(14): 4473-4485.
Zhou Dan, Sun Ke, Zhang Quanming, et al. Day-ahead robust dispatch of distribution network with multiple integrated energy system-based micro-grids[J]. Proceedings of the CSEE, 2020, 40(14): 4473-4485.
[21] 熊郁芬, 苏洁莹, 王奖, 等. 含多园区综合能源系统的配电网双层分布式调度[J]. 广东电力, 2019, 32(10): 53-61.
Xiong Yufen, Su Jieying, Wang Jiang, et al. Bi-level distributed scheduling for distribution network with integrated energy system in parks[J]. Guangdong Electric Power, 2019, 32(10): 53-61.
[22] 雷霞, 唐文左, 李逐云, 等. 考虑区域综合能源系统优化运行的配电网扩展规划[J]. 电网技术, 2018, 42(11): 3459-3470.
Lei Xia, Tang Wenzuo, Li Zhuyun, et al. Distribution network expansion planning considering optimal operation of regional integrated energy system[J]. Power System Technology, 2018, 42(11): 3459-3470.
[23] Li Chao, Miao Shihong, Zhang Di, et al. A two-stage reactive power optimization strategy for AC/DC hybrid distribution network[C]//2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 2020: 426-431.
[24] 史新红, 郑亚先, 薛必克, 等. 机组运行约束对机组节点边际电价的影响分析[J]. 电网技术, 2019, 43(8): 2658-2665.
Shi Xinhong, Zheng Yaxian, Xue Bike, et al. The effect analysis of units operation constraints on locational marginal price of unit nodes[J]. Power System Technology, 2019, 43(8): 2658-2665.
[25] Taylor J A. Convex optimization of power systems[M]. Cambridge: Cambridge University Press, 2015.
[26] 王宣元, 高峰, 康重庆, 等. 扩展的节点电价算法研究[J]. 电网技术, 2019, 43(10): 3587-3596.
Wang Xuanyuan, Gao Feng, Kang Chongqing, et al. Analysis of extended locational marginal price[J]. Power System Technology, 2019, 43(10): 3587-3596.
[27] Chen Y Q, Fink O, Sansavini G. Combined fault location and classification for power transmission lines fault diagnosis with integrated feature extraction[J]. IEEE Transactions on Industrial Electronics, 2017, 65(1): 561-569.
[28] 吴忠强, 戚松岐, 尚梦瑶, 等. 基于优化极限学习机的直流微电网并网等效建模[J]. 电力自动化设备, 2020, 40(6): 43-49.
Wu Zhongqiang, Qi Songqi, Shang Mengyao, et al. Grid-connected equivalent modeling of DC microgrid based on optimized extreme learning machine[J]. Electric Power Automation Equipment, 2020, 40(6): 43-49.
[29] 周锋, 孙廷玺, 权少静, 等. 基于集合经验模态分解和极限学习机的变压器油中溶解气体体积分数预测方法[J]. 高电压技术, 2020, 46(10): 3658-3665.
Zhou Feng, Sun Tingxi, Quan Shaojing, et al. Predication of dissolved gases concentration in transformer oil based on ensemble empirical mode decomposition and extreme learning machine[J]. High Voltage Engineering, 2020, 46(10): 3658-3665.
[30] 徐业琰, 廖清芬, 刘涤尘, 等. 基于综合需求响应和博弈的区域综合能源系统多主体日内联合优化调度[J]. 电网技术, 2019, 43(7): 2506-2518.
Xu Yeyan, Liao Qingfen, Liu Dichen, et al. Multi-player intraday optimal dispatch of integrated energy system based on integrated demand response and games[J]. Power System Technology, 2019, 43(7): 2506-2518.
Coordinated Optimal Dispatching Strategy of AC/DC Distribution Network for the Integration of Micro Energy Internet
Zheng Zhong1,2Miao Shihong1,2Li Chao1,2Zhang Di1,2Han Ji1,2
(1. State Key Laboratory of Advanced Electromagnetic Engineering and Technology School of Electrical and Electronic Engineering Huazhong University of Science and Technology Wuhan 430074 China 2. Hubei Electric Power Security and High Efficiency Key Laboratory Huazhong University of Science and Technology Wuhan 430074 China)
By connecting distributed generations (DG) to the distribution network through micro-energy-internet (MEI), it can fully utilize the characteristics of the multi-energy coupling and complementation of MEI to promote the consumption of renewable energy. This paper gave full consideration to the technical advantages of AC/DC distribution network and MEI as well as the interaction between them, and studied the optimal dispatching strategy of AC/DC distribution network considering dynamic network reconfiguration and multi-energy collaboration. Firstly, according to the characteristics of the system structure and dispatching model of AC/DC distribution network containing MEI, the coordinated operation mechanism was studied with the locational marginal price of distribution network and the bought/sold power of MEI as interactive variables. Aiming at minimizing operating cost of AC/DC power distribution network and MEI, a coordinated dispatching model of AC/DC power distribution network was established with full consideration of network operation constraints and interaction coupling constraints. Then, based on the derivation of locational marginal price of the mixed integer second order cone programming model, a fast solving method based on the extreme learning machine coupling interaction model was proposed. Finally, an example analysis was carried out on the improved IEEE 33 node AC/DC distribution network containing MEI. The simulation results showed that the scheduling architecture can fully reduce the network operation cost and promote the information interaction between the micro energy grid and AC/DC distribution network. Meanwhile, the solution technology proposed in this paper can greatly improve the solution efficiency on the premise of ensuring the calculation accuracy.
AC/DC distribution network, micro energy internet, coordinated optimal scheduling, dynamic network reconfiguration, extreme learning machine
10.19595/j.cnki.1000-6753.tces.201374
TM732
2020-10-19
2021-10-09
郑 重 男,1998年生,硕士研究生,研究方向为电网分布式发电及储能规划、电力系统凸优化。E-mail:zzheng@hust. edu. cn
苗世洪 男,1963年生,硕士,教授,博士生导师,研究方向为电力系统保护控制及微电网和主动配电网新技术等。E-mail:shmiao@mail. hust. edu. cn(通信作者)
(编辑 赫蕾)

