基于混合模型的优化低频低压减载方法研究

陈 军,陆 旭，赵子涵，向 博，朱小红

(1.国网四川省电力公司，四川 成都 610041；2.国网四川省电力公司内江供电公司，四川 内江 641003)

0 引 言

近年来，电力系统结构已经发生了巨大的改变，规模逐渐扩大，联系程度也日渐紧密[1-3]。电网公司对常见的单一故障、较严重的故障、罕见的严重故障这三级标准制定了相应的解决措施，称之为保证规模安全稳定运行的三道防线[4-5]。目前，电网公司对第一、第二道防线设备相关的在线监视、数据的信息化管控和数据的应用与分析已经逐渐趋于完善，然而对第三道防线设备数据的信息化管控能力有限[6-8]。低频低压减载属于第三道防线的范畴内。

为了保证电网在受到巨大扰动后仍然能保证电力传输的稳定性，防止频率与电压崩溃事故的出现[9-10]，下面在保证电压稳定的情况下对低频低压减载进行了研究，提出了一个集成遗传算法与人工神经网络的混合模型，在低频低压情况下进行最小化负荷切除。该方法根据潮流雅可比矩阵最小特征值灵敏度选择合适的节点进行负荷切除。

1 目标函数

建立以最小化减载量以及最大化电压稳定性为目标的目标函数[11-12]。所提目标函数F由F1和F2的组合来表示，分别用于最小化减载量与电压不稳定性，如式(1)—式(4)所示。

目标函数：

F=min{f(F1,F2)}

(1)

(2)

(3)

f(F1,F2)=γF1+(1-γ)F2

(4)

式中：f(F1,F2)为待优化的组合目标函数；F1、F2为目标函数；γ为权重因子；PLi为第i个节点的有功功率；Vi为第i个节点的电压值；fi(xmin)和fi(xmax)分别为第i个节点的最小限值和最大限值。同时，为了减少电压崩溃，使用式(3)，使电压变化的总幅度最小化。为了在保证电压稳定的情况下实现最小化减载，因此将权重因子γ设定为0.5。

为了优化上述目标函数，分别使用了等式和不等式约束，如潮流方程、雅可比矩阵的特征值、发电机的有功功率和无功功率、负荷节点的有功功率和无功功率。这些约束由以下等式详细说明。

1)功率约束用于计算当前运行条件下的功率，以及确定负载条件和减载后的功率。各节点处的无功功率平衡潮流方程如式(5)—式(6)所示。

Pi=Vi∑Vj(Gijcosθij+Bijsinθij)

(5)

Qi=Vi∑Vj(Gijsinθij-Bijcosθij)

(6)

式中：Pi和Qi分别为第i个节点的有功功率和无功功率；i=1,2,…,NB，NB为节点数量；j=1,2,…,NPQ，NPQ为PQ节点的数量；Gij和Bij分别为节点导纳矩阵第(i,j)个元素的实部和虚部。

2)在不等式约束下，考虑了发电机和负荷的有功功率和无功功率。因此，优化问题的目标函数可以在更短的收敛时间内达到。不等式约束条件如式(7)—式(10)所示。

PGn_min≤PGn≤PGn_maxn=1,2,…NG

(7)

ΔPGn_min≤ΔPGn≤ΔPGn_max

(8)

QGn_min≤QGn≤QGn_maxn=1,2,…NG

(9)

ΔQGn_min≤ΔQGn≤ΔQGn_max

(10)

式中：NG为发电机数量；PGn为第n个发电机发出的有功功率；ΔPGn为第n个发电机的有功功率变化量；QGn为第n个发电机发出的无功功率；ΔQGn为第n个发电机的无功功率变化量。选择所有节点电压的幅值作为当前状态和减载条件下的不等式约束。

Vi_min≤Vi≤Vi_maxi=1,2,…NB

(11)

3)在潮流雅可比矩阵中，选择矩阵特征值的最小值作为当前运行点和减载条件下的不等式约束。

λinitial_min(i)≥λthreshold_min(i)

(12)

λshed_min(i)≥λthreshold_min(i)

(13)

式中：λinitial_min(i)为第i个节点在正常工作点的初始最小特征值；λthreshold_min(i)为第i个节点的最小特征值阈值；λshed_min(i)为第i个节点在减载点的最小特征值。

因为最小减载量取决于系统视在功率特征值的灵敏度，所以根据潮流雅可比矩阵最小特征值对减载的灵敏度选择合适的减载节点。第i个节点最小特征值的变化Δλmin(即特征值灵敏度)由特征值变化的斜率值和负荷功率的变化计算得出。

Δλmin=xiΔPi+yiΔQi

(14)

式中：xi为相对于特征值和有功功率的斜率特性变化；yi为相对于特征值和无功功率的斜率特性变化。

(15)

(16)

式中：Δλmin_P与Δλmin_Q分别为有功功率和无功功率变化量对应的特征值变化量；ΔPi与ΔQi分别为第i个节点的有功功率和无功功率变化量。从式(14)中可以计算出特征值的变化，特征值的变化表明可以根据发电量的变化来确定最佳减载节点并给出减载量。

2 混合模型

采用遗传算法和人工神经网络相结合的方法进行减载计算。遗传算法分为两个阶段：1)构建优化模型；2)生成减载模型的数据集。遗传算法的第一阶段由式(1)在约束条件下表示。在第二阶段，使用遗传算法生成数据集，并用该数据集训练神经网络模型，进而提高减载模型的性能。根据神经网络模型，对于给定输入特征值进行减载预测。

2.1 遗传算法

遗传算法用于最小化负载有功功率变化和电压变化[13]。为了最大限度地减少负荷切除以及电压变化，遗传算法被应用于两个阶段。在第一阶段，计算雅可比矩阵的最小特征值，得出进行最小负荷切除的目标节点；然后，通过使用遗传算法的第二阶段来减少电压偏差，从而选择负荷切除的数量；最后，从这两个阶段遗传算法的结果中，产生最佳的训练数据集。

遗传算法由种群初始化、适应度评估、交叉、变异和终止5个步骤组成[14]。

1)初始化优化族群。最小特征向量是按照特征值的范围随机初始化，特征值的范围从雅可比矩阵的初始特征值中选择。

λmin=[λmin(1),λmin(2),…,λmin(i)]i=1,2,…n

(17)

式中，λmin(i)为第i个节点的最小特征值。

2)计算初始节点的适应度函数。在遗传算法的第一阶段，使用式(2)计算适应度函数；第二阶段使用式(3)计算适应度函数。

λfit_min=[λfit_min(1),λfit_min(2),…，λfit_min(i)]

(18)

Pfit_shed=[Pfit_shed(1),Pfit_shed(2),…，Pfit_shed(i)]

(19)

式中：λfit_min(i)为第i个节点最小特征值的适应值；Pfit_shed(i)为第i个节点负载功率的适应值。

3)在染色体的适应值和生成的新染色体之间进行交叉操作。在生成新的染色体之后，对新的染色体应用适应函数。

4)在突变中，根据给定的突变率对基因进行随机突变。

5)在终止阶段，根据适应度函数选择最优方案。优化过程的最优值表示为λbest_min(i)和Pbest_shed(i)，分别为第i个节点的最优特征值与第i个节点的最优减载量。然后，将最优拟合值输入于神经网络，以训练减载模型。

2.2 人工神经网络

传统减载预测中，人工神经网络的训练数据集由实际系统生成，这里采用遗传算法生成的数据作为训练数据训练神经网络。神经网络的输入为λbest_min(i)，输出为Pbest_shed(i)。神经网络由输入层、隐含层、输出层组成[15]。网络输入训练数据以及输出训练数据表示为：

λbest_min=[λbest_min(1),λbest_min(2),…，λbest_min(i)]

(20)

Pbest_shed=[Pbest_shed(1),Pbest_shed(2),…，Pbest_shed(i)]

(21)

神经网络中的反向传播训练步骤如下：

1)为每一个神经元初始化输入、输出以及权重。

2)确定输出误差E。

E=Pbest_shed-PN_shed

(22)

式中：Pbest_shed为目标输出；PN_shed为实际输出。

3)网络输出计算。

(23)

(24)

式中，wi为神经元权重。式(23)—式(24)分别为输出层与隐含层的激活函数。

4)根据式(24)改变神经元权重。

wnew=wold+Δw

(25)

Δw=x·PN_shed·E

(26)

式中，x为学习率，变化范围为0.25～0.5。

5)重复步骤2至步骤4，直到输出误差为最小值。

E<0.1

(27)

当训练完成后，神经网络将可以根据任意最小特征值确定减载量PN_shed。

3 仿真验证

将提出的混合模型减载方法在MATLAB工作平台上实现。这里采用低频低压情况下的14节点系统对所提出的混合方法的性能进行测试，评估负载最小特征值、节点电压和负载有功功率。

该14节点系统由1号和2号节点上的两台发电机以及3号、6号和8号节点上的冷凝器组成。节点电压的理想范围为0.95～1.06 pu。此系统中引发减载的原因是发电短缺。

首先，根据雅可比矩阵计算负荷节点的特征值，并根据计算出的特征值及实际功率范围确定这些节点的特征值范围。然后，计算节点的灵敏度，并根据特征值的最大灵敏度选择减载节点。

通过使用柱状图分析了混合算法的性能，并与基本情况和遗传算法的结果进行了比较。图1—图3分别展示了节点的最小特征值、电压幅值和负载功率在使用不同方法下的变化情况。

从图1可以看出，3号、4号和14号节点的特征值灵敏度最大，根据这些特征值的灵敏度，可以解决减载问题。如图3所示，在3号节点上，遗传算法计算的减载量多于混合模型计算的减载量。比较结果表明，与基本情况相比，使用混合方法进行减载可以达到最小化减载的效果。所有结果表明，所提出的混合方法可以实现最小化减载。

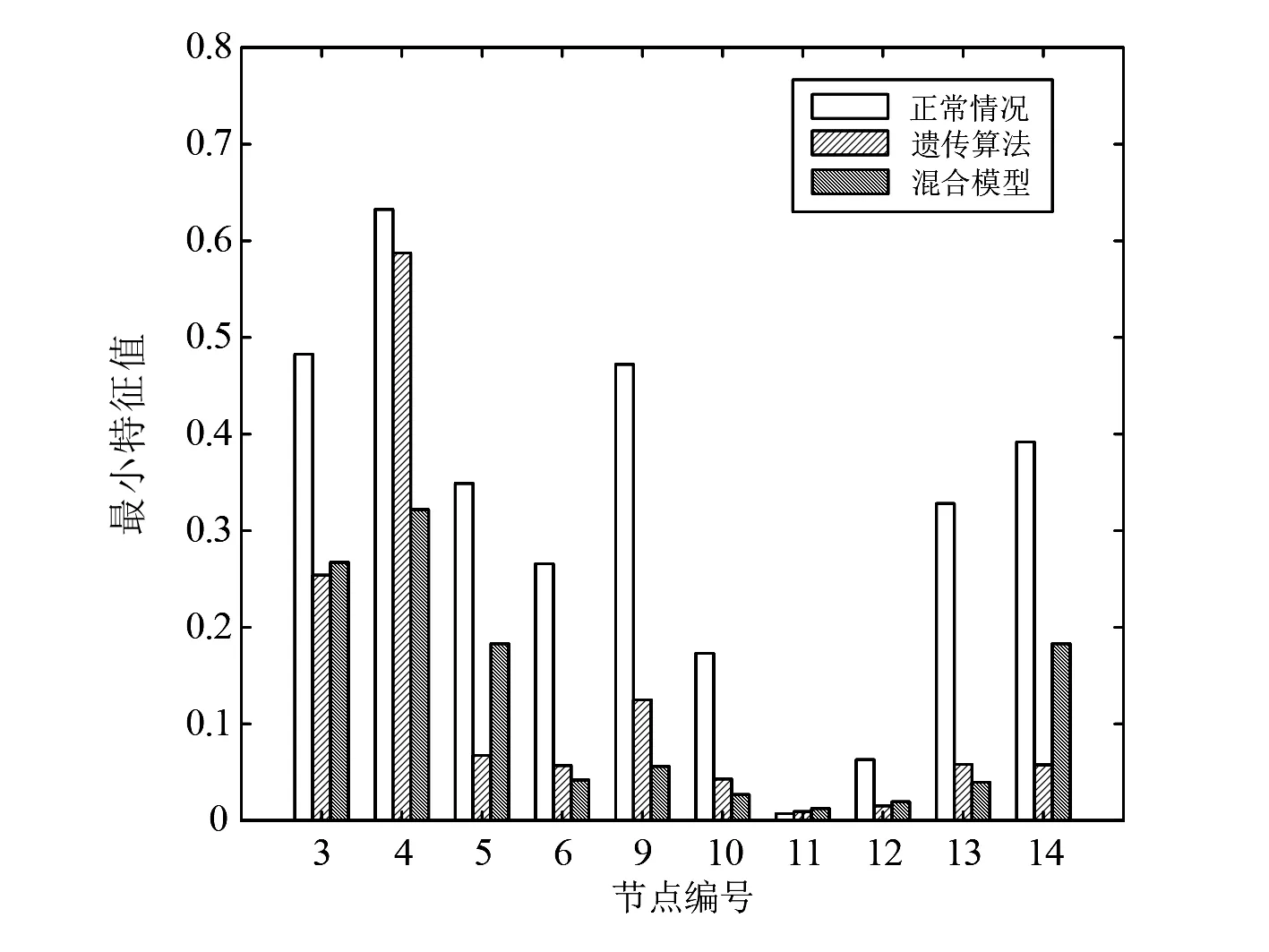
图1 最小特征值比较

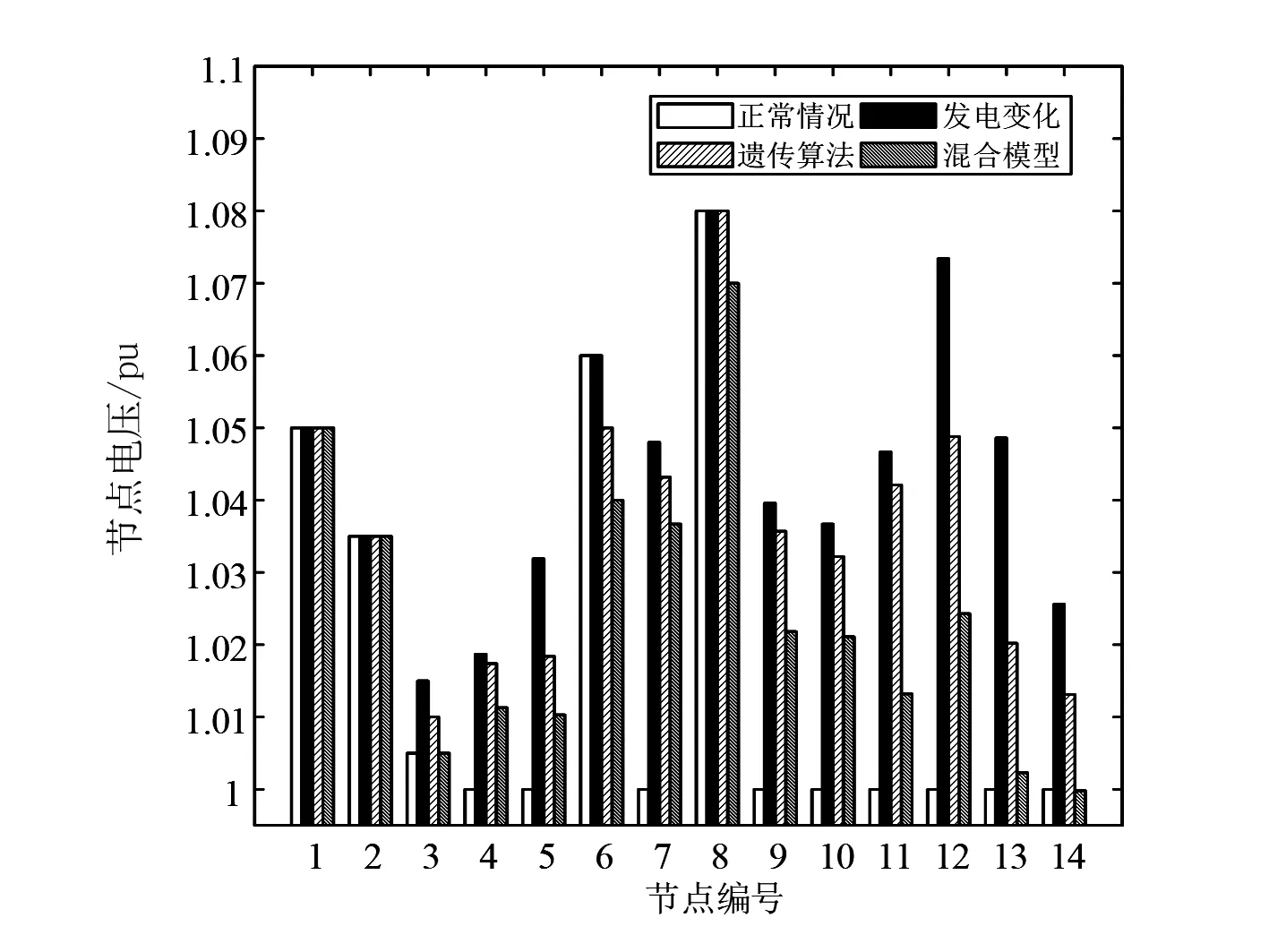
图2 节点电压大小比较

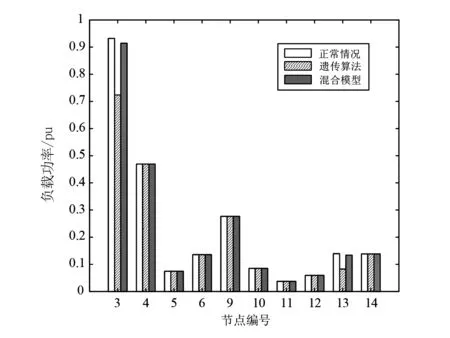
图3 节点功率变化比较

4 结 论

上面提出了一种结合遗传算法与人工神经网络的混合模型，用于在低频低压、保证电压稳定的情况下实现最小化减载的方法。在该混合模型中，遗传算法分两个阶段使用，即构建优化模型和生成用于训练网络的数据集。根据潮流雅可比矩阵最小特征值的灵敏度，选择合适的减载节点。该算法计算简单，适用于非线性问题。将该混合模型在低频低压情况下的14节点系统上进行了测试，并对其有效性进行了验证。结果表明，该方法可以在低频低压情况下实现最小化减载与最小化电压波动。