水泥混凝土路面接缝剥落破坏预测模型开发
马一娟
重庆市设计院有限公司
1 概述
水泥混凝土路面接缝处的剥落破坏可影响行车舒适性,同时由于水分在接缝处渗透,会导致更严重的路基损害。为分析剥落破坏的成因及发展恶化过程,研究人员做了许多力学性、经验性的研究。目前,基于经验数据研究的几个经验预测模型已经被广泛应用。由SHRP—P—394提出的剥落预测模型中,冻融周期和混凝土路面龄期被认为是两个主要变量,用以预测横缝处的剥落破坏。2004年,由NCHRP开发的另一种模式是基于路面龄期进行的预测,而该模型中的龄期与剥落破坏发生的路段、路面设计情况,及天气条件有关。
为了对路面结构的破坏进行预测,本文在某亚热带地区随机抽取了22个路段的监测数据,用以进行剥落破坏模型的开发。监测数据包含路面性质的变化、路面破坏(接缝破坏、裂缝、表面破损等),以及所在地区的天气和气候条件。
本文运用ABAQUS建立三维有限元模型用以模拟这些监测路段的实际路面结构,其在车辆荷载和温度翘曲作用下,通过有限元分析法计算出水泥混凝土路面接缝处的剪切应力,并运用计算出的剪应力来量化不同路段上造成剥落破坏的疲劳作用。在进行三维建模之前,已选用适当的参数作为模型的输入值,包括内部属性(混凝土弹性模量、面板厚度等)和外部因素(车辆荷载、面板温度变化等),这些参数均按照监测路段的统计数据选定。
2 预测模型的开发原理
在本次力学性-经验性预测模型的开发流程中,各监测断面的相关信息被用于三维有限元建模。
首先,三维有限元模型的几何尺寸根据实际路面结构的厚度和接缝间距确定。车辆荷载和温度荷载作为模型加载步骤之一。同时选用具有代表性的混凝土材料特性参数。建立路面结构三维模型后,再运用有限元方法分析该模型的应力响应。由于本研究认为剥落破坏是基于剪切破坏原理形成的,因此有限元分析输出的最大剪应力被用于衡量其对路面结构造成的疲劳损害,该疲劳损害被认为是导致接缝处剥落破坏的原因。
其次,对不同条件下获得的最大剪应力进行累计,以评价某一特定龄期下造成的剥落破坏程度。
最后,对这两组数据进行回归分析,采用回归方程式描述最大剪应力累计值与现场实测的剥落破坏程度间的相关性,由此获得剥落破坏的力学性-经验性预测模型。
3 有限元分析
3.1 有限元三维建模
3.1.1 模型尺寸
在ABAQUS中开发的三维有限元模型是模拟典型普通混凝土路面。该模型模拟的是弹性基础上的多层路面铺装结构系统。其中,混凝土面板、贫混凝土基层、碎石底基层的厚度分别为0.3m、0.15m、0.3m,半有限土路基厚度假设为1.0m。混凝土面板自重、面板底部与贫混凝土基层顶部间的表面摩擦作用均已考虑。混凝土单位重量采用2400kg∕m³。混凝土面板与贫混凝土基层间的摩擦系数取值0.1。
三维有限元模型中混凝土路面结构由九块面板组成。位于正中的面板尺寸为5.8m×3.8m,并由其余八块板包围。横缝和纵缝均宽7㎜,均设置有传力杆和拉杆。其中,传力杆长0.5m,直径0.032m,间距0.3m;拉杆长0.8m,直径0.127m,间距由0.75m~1m不等。单轮均布载荷被施加在面板边缘的中部,接触面积为0.25m×0.25m,荷载强度为0.64MPa,相当于半个标准当量轴次(80kN)荷载。
3.1.2 边界条件及网格划分
三维有限元模型的X坐标定义为横向接缝方向,Y坐标为纵向接缝方向,Z坐标表示路面结构深度方向。三维有限元模型的边界条件为整个系统除半无限土基层允许Z方向位移外,其余方向均固定在X、Y、Z方向上。因此,贫混凝土基层、碎石底基层、土路基均限制其在X和Y方向的位移,而本次研究的正中部面板在X、Y、Z方向均能自由移动。
为平衡计算精度要求与有限元分析复杂耗时的矛盾,模型单元类型选定为C3D8,传力杆及拉杆的单元类型为T3D2。模型中的荷载作用位置以及接缝处附近的单元采用更细的网格划分,该区域的单元尺寸为25mm×25mm×30mm。其余区域采用较粗的网格划分,最大单元尺寸为30cm×31.25cm×20cm。粗细网格间采用适当的尺寸进行过渡。整个三维有限元模型包含191,301个单元及225,116个节点。
3.1.3 材料属性及温度变化
本次研究中路面材料的属性是ABAQUS模型的必要输入参数,表1列出了三维有限元模型中各结构层材料属性的取值。

表1 水泥混凝土路面材料属性
较之车辆重复荷载,温度翘曲被认为是造成剥落破坏更为重要的原因。这一观点可通过在未开放交通的混凝土路面上发现剥落破坏的现象得以证实。
3.2 三维有限元模型数值反应
本次研究运用ABAQUS6.9分两步进行了有限元分析,用以计算模型在车辆荷载和温度变化下的应力响应。基于前述介绍的剪切破坏原理,对三维模型在不同的厚度、不同弹性模量和温度变化下发生剪切运动的应力进行计算。第一步分析考虑面板的初始温度和自重荷载,第二步分析考虑面板最终温度和0.64MPa的车辆均布载荷作用。
通过分析可见,离接缝处较远的单元产生的剪应力小于靠近接缝处的单元。最大剪应力发生在传力杆和拉杆位置。同时,受力一侧接缝处的剪应力大于不受力一侧。由图1可见,最大剪应力发生在面板横向接缝处的各单元上。由剪应力云图可知,面板中部设置传力杆的单元分布有较大的剪应力。结构中所有单元的最大剪应力则发生在纵向接缝附近施加车辆荷载的单元上。
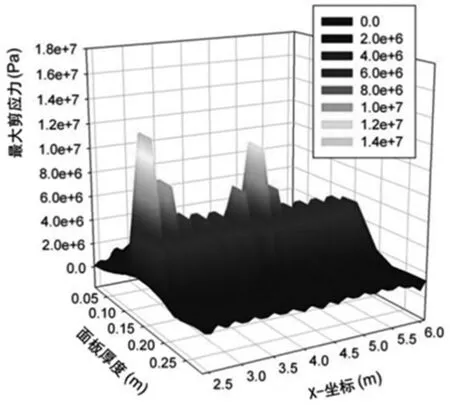
图1 面板内部最大剪应力分布
由于最大剪应力发生在传力杆、拉杆位置,以及车辆荷载施加处,因此这些单元上的剪应力被认为是力学分析中的重要评价指针。通过将混凝土路面在一定龄期范围内的最大剪应力进行累加,将其累计值与相同时间下现场实测到的剥落破坏程度建立相互关系,从而实现对剥落破坏的预测。
4 回归分析
在运用ABAQUS软件对不同路段的路面结构进行三维有限元分析后,希望可通过有限元分析计算出的最大剪应力对普通混凝土接缝处的剥落破坏进行预测。图2绘制了车辆荷载施加处产生的最大剪应力随时间推移的累计值,以及该累计值与相同时间下实测的剥落破坏的对应关系曲线。显而易见,剥落破坏的平均长度(m∕处)随最大剪应力的累计而增加。由于曲线呈指数型增长,本文运用指数曲线方程y=y0+abbx来拟合这两组数据。
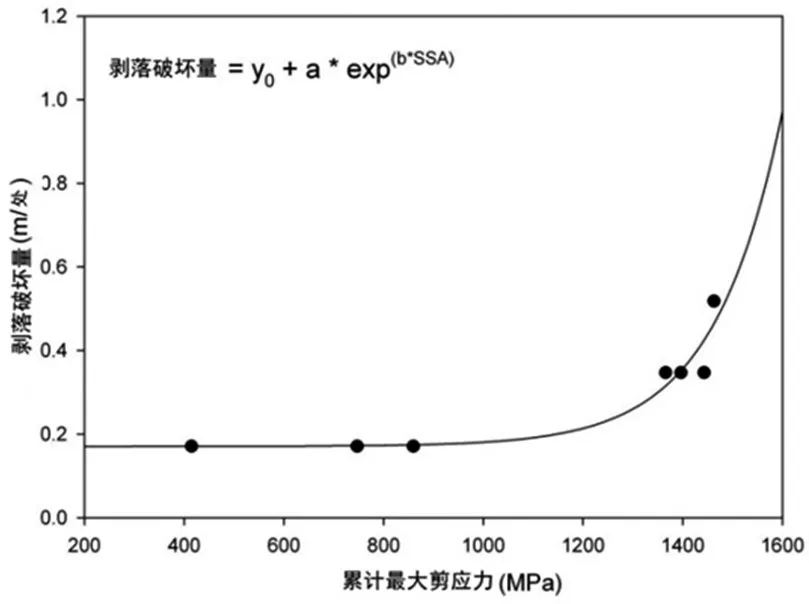
图2 剥落破坏量—累计最大剪应力的回归曲线
方程式(1)为最大剪应力累计值与路面剥落长度间指数增长关系的回归方程。该回归方程R2值为0.904,由此可判断,运用最大剪应力累计值来预测某一特定龄期的普通混凝土路面的剥落破坏程度是可靠的。
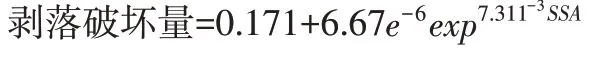
式中SSA为在t年的最大剪应力累计值。
5 结束语
本文提出了普通水泥混凝土路面接缝处剥落破坏的力学性-经验性预测模型。运用ABAQUS软件建立三维有限元模型,分析不同路面结构的剪应力。其中,最大剪应力被认为是造成混凝土板疲劳破坏的主要原因。通过绘制最大剪应力累计值与同一时间下现场实测的剥落破坏间的相互关系曲线可见,剥落破坏随着最大剪应力的累计呈指数增长。然后经回归分析,运用指数方程拟合增长曲线,从而得到预测模型。一旦获得了最大剪应力累计值,混凝土路面接缝处的剥落破坏便可通过文中提出的力学性-经验性模型进行预测。
值得注意的是,本次研究收集的剥落破坏现场数据有限。随着收集数据的增加,需要对回归模型的系数进行校正,指数模型或(和)线性回归模型可能不再适用。因此,对混凝土路面剥落破坏的长期持续监测和理论研究仍是十分必要的。

