不同材料外推模型的闭挤式精冲有限元模拟比较

袁秋 马一龙 孙汇彬

摘要： 为了解决闭挤式精冲有限元仿真准确性的问题，基于板料拉伸试验数据，建立了5种流变应力曲线外推模型。利用Deform-2D有限元软件这一平台，植入到有限元软件的功能模块，基于开发的Deform-2D有限元软件，对直径30mm、厚度14mm圆形件的闭挤式精冲成形过程进行模拟。通过物理实验，对不同流变模型的仿真结果进行比较。研究表明，Ludwik材料外推流变模型适合于闭挤式精密冲裁工艺的有限元模拟仿真，可以有效提高闭挤式精冲有限元模拟的仿真精度。

Abstract： In order to improve the accuracy of the simulation of the closed-extruding fine blanking， select five rheological equation as the closed-extruding fine blanking material stress-strain equation. Through the test data obtained from tension experiment， with the model and then extrapolated to predict the flow stress curve of the closed-extruding fine blanking. Absoft-fortran language was secondarily used to develop Deform-2D software， which combined with the stress model. Numerical simulation of a 30mm in diameter and 14mm thick round part of fine blanking process is carried out by using the software which combined with the established model and finite element method. In physical experiment，， the finite element model of realistic was verified. The results show that Ludwik extrapolation rheological model is suitable for finite element simulation of the closed-extruding fine blanking， and improve the accuracy of this model.

關键词： 闭挤式精冲;流变应力;外推模型;有限元

Key words： closed-extruding fine blanking;flow stress;rheological model;finite element

中图分类号：TG381                                      文献标识码：A                                  文章编号：1674-957X（2022）03-0020-03

0  引言

闭挤式精密冲裁，是通过在变形的过程中使坯料始终被限制在有限的模具型腔内，使得变形区获得比强力压边精冲更强的三向压应力，以此来提高变形区材料的塑形，实现精冲低塑性材料和厚板目的的一种成形工艺[1-3]。利用Deform有限元软件模拟精冲过程，对工艺参数进行优化，是一种有效且经济的方法[4]。闭挤式精冲属于大应变变形，其材料剪切变形真实应变值在4以上。但在Deform材料库中，其材料的流变曲线应变范围较小，一般在2左右[5]。在变形后期，当材料应变值超过其应变范围后，不能有效确定材料应力值大小。因此，对不同材料外推模型进行拟合分析，建立准确的闭挤式精冲有限元模型就显得十分必要。

本文初步选取5种流变模型作为闭挤式精冲材料的实验模型[6]。通过拉伸试验得到了小变形下材料的变形数据，再对初始数据进行拟合，得到了外推流变应力模型。利用Deform-2D有限元软件这一平台，将建立的外推流变应力模型通过编程软件Absoft fortran编译成能够植入到有限元软件的功能模块，即对模拟软件进行二次开发，建立起闭挤式精冲的有限元模型。基于开发的Deform-2D有限元软件，通过对直径30mm、厚度14mm的圆形件进行闭挤式精冲成形过程进行模拟。从静水压应力、断裂带、塌角和行程载荷四个方面对不同流变模型的仿真结果进行比对，并通过物理实验验证，找出了适合于闭挤式精冲的流变外推模型。

1  外推模型建立

1.1 拉伸试验

在万能试验机上面，选取材料为20#，直径d=10mm的圆形截面比例试样进行拉伸试验。拉伸试验过程中，拉伸试样的位移变化是通过应变引伸仪去测量出来的，然后再把测量出来的数据转化为电信号传入到计算机中，然后计算生成材料的真实载荷-位移曲线[7-8]。从计算机中导出材料载荷-位移曲线数据，通过对应的公式换算得到材料的真实应力-应变曲线，如图1。

1.2 曲线拟合

通过拉伸实验测得的真实应力-应变数据，以此来作为建立材料本构方程的初始数据，进行材料流动应力模型的拟合，得到了各模型的小变形流变曲线。再根据拟合数据进行外推，得到了各模型的大变形流变曲线。本文选取了5种材料流动应力模型，分别是H-S、Voce 、Ludwik、Voce++和Hollomon，对它们的函数曲线进行拟合，并得到其拟合的函数方程，如表1所示[9]。

图2为拟合的5种外推流动应力曲线。如图所示，随着应变量的继续增加，H-S、Voce外推流动曲线趋于水平线，属于饱和曲线模型。Ludwik、Voce++和Hollomon这三种外推流动曲线并无应力极值，属于非饱和曲线模型。其中，Voce++、Ludwik模型其流动应力随着应变值增加快速增大，属于强硬化模型;Hollomon模型则属于弱硬化硬化模型。对于闭挤式精冲有限元仿真来说，结合闭挤式精密冲裁过程中材料加工硬化增强，大变形的变形特点，选取合适的材料流变模型进行仿真分析。

2  有限元模型建立

2.1 有限元模拟工艺参数条件确定

采用有限元模拟仿真方法，对闭挤式精冲成形过程进行模拟计算。图3所示为有限元模型和工艺参数，采用DEFORM-2D软件进行分析，模拟进行的实验参数设置如表2所示。

坯料设置为弹塑性材料，模具中的凸模、主凹模、副凹模、反顶板全部设置为刚性體。一共划分了60000个矩形单元网格，针对塑性变形较大的凸、凹模间隙附近材料进行网格局部细化，从成形面到材料内部网格细化比例因子为0.1∶0.3∶1.0[10]。考虑到静水应力对断裂的影响，选用Brozzo断裂准则，可以较好的预测精冲过程中剪切面发生的断裂情况[11-12]。利用Deform-2D有限元软件这一平台，将建立的外推流变应力模型通过编程软件Absoft fortran编译成能够植入到有限元软件的功能模块，建立起闭挤式精冲的有限元模型。

2.2 模拟结果及讨论

通过前面拟合的5种外推流动应力曲线结果，选取Ludwik强硬化外推模型进行估测，同时选择Hollomon弱硬化硬化模型和Deform-2D软件自带的模型作为比较。结合物理实验结果，对这3种材料外推模型下精冲有限元模拟结果进行对比，从中选出适合于闭挤式精冲的材料流变模型。

2.2.1 静水应力分布

对3种模型模拟结果进行对比，可以看到3种模型下所得到的静水应力分布都符合理论静水应力分布趋势，即在开始冲裁阶段，在主、副凹模闭合型腔施加的压力作用下，变形区静水压力较大，随着冲裁行程的继续增加，静水压力值开始逐渐减小。当凸模压入1/3板料厚度时，变形区材料处于压应力状态，但当凸模继续下压到2/3板料厚度时，变形区静水压力逐渐减小，甚至出现了拉应力现象。再加上成形过程中材料出现的冷作硬化现象，造成了材料塑性降低，所以在精冲末期很容易产生裂纹。所以在闭挤式精冲工艺的后期，为了保证所加工的零件具有光洁的冲裁面，对促使裂纹产生的拉应力采取有力的平衡措施是十分必要的。

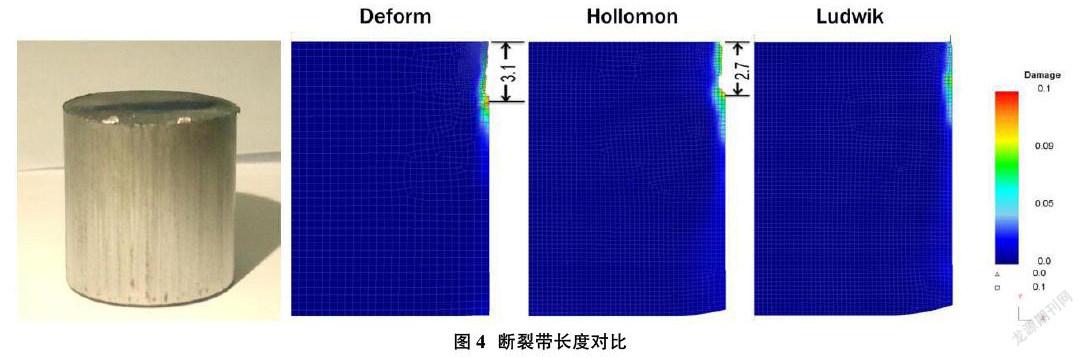
2.2.2 断裂带分布

图4是利用选取的3种流变模型进行模拟仿真所得到的剪切面断裂带长度对比图。从损伤模拟结果上看出，三种流变应力模型都明显模拟出了剪切面损伤的理论变化趋势，即当凸模压入1/5～3/5板料厚度过程中时，它们的损伤值并没有随着凸模的下行而增大;但当凸模压入3/5料厚开始，直至全部压入板厚过程中，其损伤值明显增大，并且越是接近冲裁的末期，其损伤值增长幅度越大[8]。究其原因，问题主要集中在两个方面：一个是在精密冲裁的末期，由于施加的压边力、反顶力不足，使得模具刃口附近材料的静水应力快速减小，甚至转变成为正值，这就加快了材料损伤的发展;二是由于成形过程中材料产生的加工硬化现象，随着精冲过程的持续进行，材料变形程度不断加大，变形区材料本身的硬度和强度不断增大，但材料塑性和韧性却不断降低。特别是在精冲末期材料所受到的加工硬化作用更加明显。

图4左边为物理实验得到的零件真实剪切面，然后对试件表面与模拟成形面结果进行比较。从实验中得到的试件表面其剪切面比较光滑，并且达到了全光亮带。试件的上端面略有毛刺产生，下端面有很小的塌角产生。试件表面有一条条印痕，这是由于凹模的“复印效应”产生的[8]。比较三种模型的剪切面模拟结果，Deform模型和Hollomon模型均产生断裂，断裂带长度分别达到3.1mm和2.7mm，Ludwik模型剪切面达到全光亮带，且在成形面上端有少量毛刺产生。从图中可以明显看出，Ludwik模型得到的模拟结果与物理实验结果更为接近。

2.2.3 行程载荷比对

图5为利用选择的3种流变模型进行模拟所得到的负载曲线。从图中可以明显看出，三条负载曲线形状都呈现出了先增加后减小的总体趋势。即在精冲开始阶段，其承受的负载迅速增大，当达到一个峰值后，逐渐递减，直至出现断裂。这是由于在冲裁刚刚开始的时候，材料变形量较大，材料硬化作用对负载的影响较大，造成负载短时间内急剧增大。当随着精冲过程的继续进行，零件剪切面积逐渐减小，负载力则开始慢慢降低。对三种流变模型得到的行程载荷曲线与实际物理实验载荷曲线结果进行比较，从成形力变化趋势这个方面来看，Ludwik模型与实际成形力值变化更为一致。物理实验得到的实际冲裁力为445kN，Ludwik模型得到的最大冲裁力为441kN，更加接近于实际冲裁力。因此，选用Ludwik模型进行闭挤式精冲成形仿真，其模拟结果更加符合实际情况。

3  结论

①对三种模型计算结果与物理实验结果进行比较，发现选取Ludwik流变应力模型进行计算，其模拟仿真结果更加符合闭挤式精冲物理实验结果。

②选取Ludwik、Hollomon和Deform自带流变模型进行计算，其模拟结果相差很大，说明不同的流变应力外推模型对有限元模拟仿真结果还是有比较大的影响。因此，在进行有限元建模时，应该根据材料实际变形情况，进行材料流变应力模型的选取。

参考文献：

[1]邓明，张会杰，吕琳，等.闭挤式精冲工艺及其材料流动机理[J].锻压技术，2009，34（6）：38-40.

[2]邓明，张会杰，吕琳，等.基于物理实验的闭挤式精冲工艺研究[J].锻压技术，2010，35（2）：69-72.

[3]邓明，孙成亮.低塑性厚板的精密轮廓对向凹模冲裁技术及应用[J].中国机械工程，2006，17（20）：2179-2182.

[4]邓明，张会杰，吕琳，王正立.闭挤式精冲工艺及其成形规律[J].锻压技术，2009（6）：43-46.

[5]王少阳，陈文琳，李志杰.不同材料外推模型的精冲有限元模拟对比[J].精密成形工程，2011（5）：9-13.

[6]李宏烨，庄新村，赵震.材料常用流动应力模型研究[J].模具技术，2009（5）：1-4.

[7]J. Kleemola H， A. Nieminen M. On the strain-hardening parameters of metals[J]. Metallurgical & Materials Transactions B， 1974， 5（8）：1863-1866.

[8]马一龙.闭挤式精冲成形力学分析及有限元建模[D].重庆：重庆理工大学，2015.

[9]邓明，马一龙，刘潞周，吕琳，袁秋.基于正交方案的闭挤式精冲直齿轮工艺参数优化[J].重庆理工大学学报（自然科学）》，2014.

[10]邓明，王正立，吕琳.闭挤式精冲变形区应力状态对断裂损伤的影响[J].塑性工程学报，2011，18（001）：67-71.

[11]方刚，雷丽萍，曾攀.金属塑性成形过程延性断裂的准则及其数值模拟[J].机械工程学报，2002，12（38）：21-25.

[12]张会杰，吕琳，邓明.闭挤式精冲工艺过程的数值模拟及参数优化[J].《锻压装备与制造技术》，2010，45（2）：73-76.