泄洪雾化水滴分档随机喷溅数学模型及其验证
张 华,何贵成
(华北电力大学水利与水电工程学院,北京 102206)
水利工程在挑流泄洪时,产生的高速水舌与空气掺混[1],两股水舌碰撞,以及水舌和下游水面的撞击,都会形成大小不一的雾源。雾源处喷溅的水滴,在坝下游沉降,产生强度远大于自然降雨的泄洪雾化降雨[2-3]。严重的泄洪雾化会影响电站电气设备的正常运行、冲蚀地表,影响岸坡稳定和厂区交通等[4-5]。研究泄洪雾化的产生机理、雾源强度、扩散规律、以及降雨强度,对采取合理措施减轻泄洪雾化的危害具有重要价值[6]。
泄洪雾化降雨范围和大小的计算,常用原型观测[7]、理论分析[8]、模型试验[9]和数值模拟[10-11]等方法。梁在潮[12]详细描述了泄洪雾化现象,推导出了水舌掺气量、溅水影响区域和雾流扩散的理论计算公式。刘宣烈等[1]采用立体摄影和电阻式掺气仪两种测量方法,试验得到了水舌断面掺气浓度、沿程变化与参数的关系。张华等[13]在观测与试验数据的基础上,提出了水滴随机喷溅数学模型,应用较为广泛[14-16]。水滴随机喷溅数学模型在初始条件中采用多个随机变量以模拟水滴在雾源喷出时的随机特性,随机变量包括喷溅水滴的直径、速度和偏移角等。
在水滴随机喷溅数学模型基础上,学者进行了模型的适用性验证,以及改进工作。如在双江口水电站数学模型喷溅试验[17]的数值计算中,水面以上的下垫面为自然地形,验证了水滴随机喷溅数学模型在复杂地形情况下的适应能力。两河口水电站的泄洪雾化计算中[18],引入水舌风的作用,在数学模型中增加考虑了水舌风对喷溅水滴运动的影响。
水滴随机喷溅数学模型,通常采用蒙特卡洛方法[19]进行求解,即生成大量符合假设随机变量分布的随机水滴,最后统计水滴停止运动后的分布情况,由此获得雾化降雨大小。由于雾化降雨大小由随机水滴统计产生,因此受到水滴样本数量的影响较大。为得到较准确的雾化降雨数值,水滴随机喷溅数学模型常需要生成几百万的水滴作为样本,计算量大、效率低。
云物理学理论[20]为计算云滴谱随时间和高度的演变情况[21],采用的方法是将云滴按照大小划分为若干档[22],然后随着时间步的增加,云滴自然凝结生长,云滴大小越出原档,各档云滴数量也随之增减,从而计算出云滴谱的演变情况。在燃油喷雾数值模拟[23]中,离散液滴数学模型[24]并不会计算所有油滴的运动,而是选取计算若干具有代表性的样本油滴的运动轨迹[25],提高了计算效率。在模拟流化床[26]的颗粒流动算法中,如OpenFOAM的DPMFoam求解器[27],采用了颗粒微团,即多个颗粒的集合,并假定集合中的颗粒具有相同的尺寸和速度。上述方法的目的都在于减少计算雾滴、油滴和颗粒的数量,以降低对内存和计算能力的需求。
因此,本文基于云滴分档、代表性油滴和颗粒微团等降低计算量的思想,提出分档水滴的概念,建立挑流泄洪雾化的水滴分档随机喷溅数学模型,并在假定条件下对模型进行对比验证。
1 水滴运动微分方程及其解析解
1.1 水滴运动微分方程
如图1所示,假设在直角坐标系Oxyz的O点处,抛出N个水滴,初始速度为v,速度与Oxy面的夹角为出射角β,速度与Oxz面的夹角为偏移角φ。从原点处抛出的水滴做斜抛运动,当水滴接触Oxy面时,则停止下来。在某个时间间隔内,通过统计水滴在水平面上的质量分布情况,即可求得雾化降雨的数值。

图1 水滴喷溅示意图
考虑水滴在运动过程中受到浮力、重力和空气阻力的作用,则水滴的运动微分方程[13]为
式中:Cf为空气阻力系数;d为水滴直径;ρ为水滴密度;ρa为空气密度;vw为水滴速度;va为环境风速(vax、vay、vaz分别是3个坐标轴上的投影);g为重力加速度。
水滴运动微分方程的初始条件为

(2)
式中:v为水滴的初始速度;β、φ分别为水滴的出射角和偏移角。
1.2 水滴运动微分方程的解析解
式(1)是一个二阶非线性微分方程组,不能得到其解析解。对其做解耦合线性化的处理,转变为二阶线性微分方程组,得到:
(3)
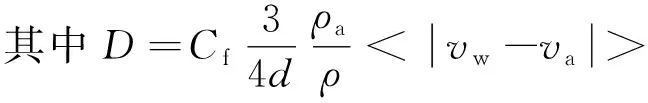
式中:<|vw-va|>为水滴速度与环境风速差值的系综平均。
由初始条件(2),并假设环境风速va为常数,可以得到式(3)的解析解:
(4)
令z(ta)=0,可以获得水滴接触Oxy平面的时间ta的计算公式如式(5)所示,然后可以得到水滴停留在Oxy平面上的位置为(x(ta),y(ta))。
(5)
若假定v、β和φ为随机变量,并服从联合概率密度分布f(v,β,φ),则由连续型随机变量的函数的分布理论[28],式(4)的多元函数所对应的概率密度分布为
fp(x(t),y(t),z(t))=f(v(x(t),y(t),z(t)),
β(x(t),y(t),z(t)),φ(x(t),y(t),z(t)))|J|
(6)

2 水滴分档随机喷溅数学模型
在水滴随机喷溅数学模型[13]中,水滴的初始速度v、出射角β和偏移角φ,均为随机变量,模型通常采用蒙特卡洛方法进行求解。
为了改进蒙特卡洛方法计算量大、效率低的缺点,基于云滴分档[22]、代表性油滴[25]和颗粒微团[27]等学术思想,提出水滴分档随机喷溅数学模型。主要改进内容为,根据水滴初始参数相空间进行分档化处理,由此形成分档水滴,并让一个分档水滴携带概率信息,以代表多个水滴,最终减少实际的计算量,提高计算效率。
2.1 水滴初始物理参数的相空间
将水滴的初始参数v、β和φ所构成的物理空间,称为水滴运动初始物理参数的相空间,记为Γ(v,β,φ),如图2所示。相空间中的一个相点表示单个水滴的初始状态,整体表示水滴所有可能的初始状态。

图2 水滴初始物理参数的相空间示意图
2.2 相空间分档方法
水滴初始物理参数相空间的分档方法如下:
a.水滴初始速度的分档。对v做均匀分布的分档化处理[22],这里划分为I档,每档的大小为a,则每个档的速度vi为
vi=ai(i=1,2,…,I)
(7)
b.水滴出射角的分档。对β也同样做均匀分布的分档化处理:分为J档,每档的大小为b,则出射角βj为
βj=bj(j=1,2,…,J)
(8)
c.水滴偏移角的分档。对φ也做均匀分布的分档化处理:在其定义域内均匀分为K档,每档的大小为c,则偏移角φk为
φk=ck(k=1,2,…,K)
(9)
2.3 分档水滴及其概率值计算
水滴运动初始物理参数相空间通过分档之后,形成相格(图2中长方形线框)。一个相格中包含了多个相点,即内含多个水滴的初始状态信息。用一个代表性相点,来表征整个相格中所有相点,称这个代表性相点对应的水滴为分档水滴。分档水滴所对应的概率密度为
Pijk=f(vi,βj,φk)
(10)
3 微分方程和数学模型的求解
为了获得水滴运动微分方程组的解析解,并以此为基准,评价水滴随机喷溅数学模型和水滴分档随机喷溅数学模型的数值解的精确度,从而验证水滴分档随机喷溅数学模型的求解精度。
在不改变微分方程组本质的情况下,为对公式(1)进行简化,提出如下两个假定条件:①忽略空气阻力和浮力作用;②随机变量v和β取为定值,φ的概率密度函数fφ满足正态分布:
(11)
3.1 水滴运动线性微分方程的解析解
在假定条件下,得到下列参数的数值:阻力系数Cf=0,空气密度ρa=0 kg/m3。代入式(3),得到水滴位置随时间的函数关系为
(12)
令z(ta)=0,则水滴经过一段时间ta,因接触Oxy面而停止运动,可以得到水滴停止运动时的位置与φ的函数关系为
(13)
由于fφ为正态分布,绝大部分水滴位于(-3σ,3σ)范围内,因此可取φ的定义域为C=(-π/3,π/3)。

y(φ)的反函数为
(14)
由假设条件②,已知φ的概率密度函数,以及式(6),可得到水滴在y轴上投影的概率密度函数为
为便于解析解与数学模型的数值解进行对比,对解析解进行离散化处理。将值域S均匀分为M个数量的组,组距为h,即第m组的取值范围是[hm-1,hm),分组形式记为集合A={[hm-1,hm)|m=1,2,…,M}。则水滴处于第m组内的概率密度的解析解为
(16)
3.2 水滴随机喷溅数学模型的数值解
水滴随机喷溅数学模型采用蒙特卡洛方法求解,生成的水滴为随机产生,现生成N个水滴,其中的偏移角使用随机数发生器产生,记为φn,r(n=1,2,…,N),它满足概率密度函数fφ。
根据式(13),可以计算水滴偏移角为φn,r时,相应在y轴上的运动距离为yn,r。依据分组集合A,统计yn,r在第m个分组范围内的水滴的个数,记为qm,r,计算公式为
(17)

得到水滴处于第m组的概率密度为
(18)
3.3 水滴分档随机喷溅数学模型的数值解
水滴分档随机喷溅数学模型,生成的分档水滴,在定义域内均匀分布,并且包含概率信息,具体的计算步骤如下:
步骤1由假定条件②,只需要对φ进行分档处理,因此在其定义域内,产生N个分档水滴,每个分档水滴的偏移角由式(9)计算,记为φn,g(n=1,2,…,N)。
步骤2根据概率密度函数fφ,以及式(10),计算得到偏移角为φn,g的分档水滴所对应携带的概率pn,g为
pn,g=fφ(φn,g)c
(19)
步骤3由式(13)计算出分档水滴在偏移角为φn,g时,在y轴上的运动距离yn,g。
步骤4依据分组集合A对分档水滴在y轴的距离进行分组,得到处于第m组范围水滴的概率qm,g为
(20)
步骤5得到水滴处于第m组范围的概率密度为
(21)
4 案例计算与结果分析
式(1)是非线性微分方程组,一般情况下,只能采用数值模型进行求解。若不进行参数简化,仅能得到两个数学模型的数值解。没有解析解的准确值作为基准,无法判别两种数值模型的计算结果的误差大小。案例是在两个假设条件下,对微分方程组中的参数进行简化,获得解析解式(15),并以此作为后续两个数值解计算误差的对比基准。
在两个假定条件下,选取v=10 m/s,g=9.81 m/s2,β=π/5,M=100。根据上述3种求解方法,可以分别得到解析解和两个模型的数值解,并对计算结果进行对比和误差分析。
水滴随机喷溅数学模型生成的100个水滴的偏移角φ的分布如图3(a)所示,在概率密度较小的区域,生成的水滴个数过于稀少,甚至为0。图3(b)为水滴分档随机喷溅数学模型产生的100个分档水滴的偏移角分布情况,在定义域内非常均匀。

图3 两个数学模型所产生水滴的偏移角分布
4.1 水滴随机喷溅数学模型的数值解
当水滴总数分别为1 000、1万、10万和100万时,采用水滴随机喷溅数学模型的求解结果如图4所示。
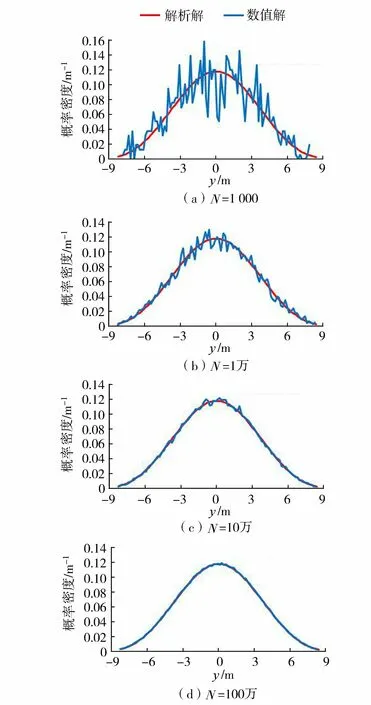
图4 水滴随机喷溅模型的数值解与解析解
当水滴总数为1 000时,水滴随机喷溅数学模型的数值解相比解析解有较大的误差,误差的波动幅度也很大(图4(a))。水滴个数达到1万时,数值解虽然局部与解析解仍然有较大偏差,但误差明显减小,误差的波动幅度也缩小(图4(b))。随着水滴个数继续增加,水滴随机喷溅数学模型的求解误差依然比较为明显,但继续减小(图4(c)(d))。
4.2 水滴分档随机喷溅数学模型的数值解
分档水滴总数分别为1 000、1万、10万和100万时,采用水滴分档随机喷溅数学模型的数值解结果如图5所示。

图5 水滴分档随机喷溅模型的数值解与解析解
分档水滴总数为1 000时,结果如图5(a)所示,水滴分档随机喷溅数学模型的数值解与解析解的差异较大,但相比图4(a)要小许多,波动幅度相比也更小,呈现相对规律的锯齿状。当分档水滴个数增加10倍达到1万时的结果如图5(b)所示,整体误差已经较小,已看不出数值解与解析解有明显差异。再继续增加分档水滴的个数(图5(c)(d)),对计算精度的改善作用已经很小。
对比图5(b)和图4(d)可见,1万个分档水滴的误差,已能达到水滴随机喷溅数学模型使用100万个水滴求解时的水平。
4.3 误差分析
为量化水滴随机喷溅数学模型和水滴分档随机喷溅数学模型数值解的求解精度,评估数值解与解析解之间的误差大小。这里采用最大误差η和平均误差ε两个指标进行评价,计算公式如下:
(22)
(23)
式中:pm,a为第m个分组的解析解;pm,s为第m个分组的数值解。
误差分析结果如表1所示。随着水滴个数的增加,水滴随机喷溅数学模型和水滴分档随机喷溅数学模型的误差均逐渐减小。在水滴总数为1万时,平均误差指标已比较小,分别为11.46%和3.86%;最大误差也迅速降低,水滴随机喷溅数学模型的误差从143.81%降至63.58%,水滴分档随机喷溅数学模型的误差从19.42%下降至12.94%。

表1 两个数学模型的数值解误差和计算所需时间对比
随水滴总数的变化,在两个模型的水滴个数相同,甚至较少的条件下,水滴分档随机喷溅数学模型的最大误差会更小。如在水滴总数为1万时,水滴分档随机喷溅数学模型的最大误差为12.94%,已经比水滴随机喷溅数学模型在水滴总数为100万时的15.26%更小。
进一步对两个模型的平均误差,也显示出水滴分档随机喷溅数学模型的精度更高。当水滴分档随机喷溅数学模型在水滴总数为1万时,平均误差已经下降到3.86%,而水滴随机喷溅数学模型在总数达到100万时,平均误差才下降为3.66%,两者误差十分接近。
最后从收敛趋势来看,水滴随机喷溅数学模型,水滴总数从1 000增加到100万时,最大误差从143.81%,降低为15.26%,一直在逐渐下降。而水滴分档随机喷溅数学模型在水滴总数从1 000增加到1万后,继续增加水滴个数,误差变化不大。表明了水滴分档随机喷溅数学模型的误差收敛速度更快。
4.4 两个数学模型计算所需时间分析
在i7-3 770处理器、24GB内存的计算机配置,以及Win7系统、Python 3.5.2编程环境的条件下,两个数学模型计算所需时间如表1所示。水滴总数从1 000到100万,水滴随机喷溅模型的计算所需时间,从0.002 8 s增加到0.405 4 s;相对应的,水滴分档随机喷溅模型计算所需时间从0.002 1 s增加到0.362 6 s。同一个数学模型,水滴总数越大,计算所需时间越长,呈现线性关系。
在相同水滴总数情况下,两个数学模型计算所需时间的相对差异并不是很大,处于同一个数量级,但水滴分档随机喷溅模型所需时间更少。在水滴总数为1 000时,计算所需时间分别为0.002 8 s和0.002 1 s;而在水滴总数为100万时,计算所需时间分别为0.405 4 s和0.362 6 s。
随着水滴总数的增加,两个数学模型计算所需时间相差会更大。在水滴总数为1 000时,两个数学模型计算所需时间相差0.000 7 s;而在水滴总数为100万时,两个数学模型计算所需时间相差0.042 8 s。
参与计算的水滴总数越大,两个数学模型的数值解与解析解的误差越小。在水滴总数相同的条件下,水滴分档随机喷溅数学模型的误差明显更小,模型的计算所需时间也更少。水滴分档随机喷溅数学模型可以采用更小的水滴总数,减少所需计算时间,同时保证计算的准确度,从而提高了计算效率。
5 结 论
a.针对水滴随机喷溅数学模型计算量大,效率较低的问题,提出了分档水滴的新概念,建立了挑流泄洪雾化的水滴分档随机喷溅数学模型。
b.在两个假定条件下,对水滴分档随机喷溅数学模型进行了验证计算,结果显示该模型具有更好的求解精度。其中1万个水滴的分档随机喷溅数学模型的求解结果,非常接近100万个水滴的随机喷溅数学模型的求解精度。
c.在水滴总数相同的情况下,水滴分档随机喷溅数学模型计算所需时间更少,同时其数值解的误差也更小,表明水滴分档随机喷溅数学模型的计算效率更高。

