基于卷积神经网络的板形缺陷识别*

胡 鹰 孙绍宁 乔磊明

（太原科技大学计算机科学与技术学院 太原 030024）

1 引言

随着时代的进步发展，板材在我们日常生活中的应用越发广泛，然而板材的生产不是一个完美的过程，外部原因可能导致板材有许多不同类别的缺陷。板材质量不合格不仅影响矫直机作业的速度和质量，严重的甚至会造成机械报废［2］。

传统的板形缺陷识别大多依靠人的经验［5］，不仅工作效率低下，而且容易受到人力因素的干扰。有经验的工人毕竟是少数，一旦工作量较大时往往会因人手不够导致工作无法进行下去。随着时代的发展，人力操作逐渐被人工智能所取代。板形仪作为当代测量板形数据常用的仪器［5］，在国外的应用较为广泛，在国内还没有普及。国内大多是利用径向基（Radial Basis Function，RBF）神经网络和BP（Back Propagation）神经网络进行板形缺陷的识别［10］。但现有的方法只能纠正简单的板形缺陷，不能识别稍复杂的缺陷。

为了解决板形缺陷识别精度不高、操作复杂和成本过高等问题，提出了一种基于卷积神经网络的板形缺陷识别模型（OP-AlexNet）。

2 相关工作

目前，很多学者针对板形缺陷识别问题做了许多研究。冯晓华等将遗传算法与BP算法相结合，让网络结构能随着板宽的变化而变化，使得网络结构灵活多变［17］，减少了训练所需样本，提高了神经网络的学习能力和收敛性。解相朋等利用粒子群优化算法优化了径向基神经网络的结构，增强了网络的泛化能力，提高了板形识别的精度［11］。张秀玲等通过对聚类算法的优化，提出了SOM聚类方法，对RBF和BP神经网络进行混合优化从而提高了板形识别的精度，同时相比之前的方法计算量减少，网络模型的鲁棒性也更强［10］。但不论是RBF还是BP神经网络模型都需要精密仪器测量数据，操作复杂且成本过高。

自LeNet-5诞生后陆续诞生了AlexNet、VGGNet、Inception等经典卷积网络模型相继问世并得到广泛应用［13］。严飞等改进了CNN图像语义分割方法并应用于木材缺陷识别。但由于结构相对简单效果并不出众［8］。姜洪全等改进了卷积神经网络模型结构建立池化模型并应用于焊缝缺陷识别，通过对池化层的改进提升了模型的特征提取能力，从而提高了焊缝缺陷识别的精度［20］。陈立潮等改进了经典的AlexNet模型并应用于不锈钢焊缝缺陷分类中，通过冻结网络的前三层减小网络对输入数据量的限制，之后采用BN层代替原模型的LRN层以提高网络训练速度，并使用LeakyReLU函数对抑制神经元进行重新激活，从而提出一种融合迁移学习的AlexNet神经网络不锈钢焊缝缺陷分类模型并达到了较好的效果。但是上述方法均在不同于板形识别的领域且不同程度的存在一定不足，例如BP神经网络的连接权值、节点数以及网络层数等参数过多，工作量庞大。不同领域的模型参数不同，且受材料、加工等多方面因素影响，因此不能直接用于板形缺陷识别当中。

综上，为使板形缺陷识别的操作更为简单、成本更低以及识别更加准确，本文提出OP-AlexNet模型对各种板形缺陷进行识别。

3 准备工作

3.1 卷积神经网络

卷积神经网络于1987年被提出并应用，当时的神经网络存在内存和内部参数占用过多的问题，卷积神经网络的出现很好地解决了这些问题［1］。整个网络主要包含卷积层、池化层、全连接层这三个部分［18］。图1为卷积神经网络的结构。

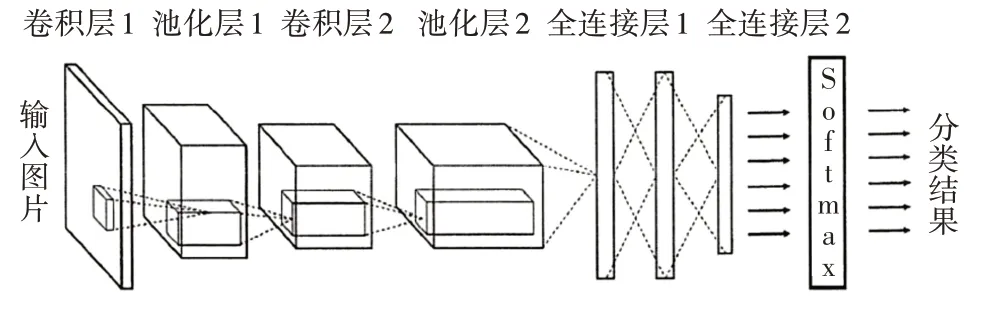
图1 卷积神经网络结构

卷积层的正向传播映射为

偏置项的偏导数为

定义误差项为

则有：

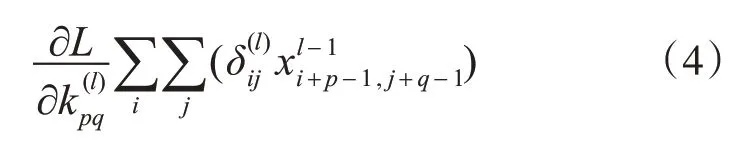
在卷积层后的是池化层，它的作用是将提取的特征进行分割。假设池化层输入为x(l-1)，输出为x(l)那么将有以下定义：

上式为下采样操作，同理可得上采样计算误差项为

最后是全连接层，它的作用是将提取到的特征信息组合在一起，识别出种类。

3.2 AlexNet模型

AlexNet由Alex Krizhevsky于2012年提出［21］。AlexNet提出后深度学习开始迅速发展。图2为AlexNet模型的网络结构示意图。

图2 AlexNet网络结构示意图

由图2可以看出AlexNet模型具有5层卷积层、3层池化层以及3层全连接层［15］。激活函数采用ReLU进行运算，ReLU函数的公式为

AlexNet是多GPU并行运算，其输出大小为

其中n为输入图片的大小，p为填充像素，f为过滤器，s为步长。

AlexNet在图像处理方面有着广泛的应用且相较其它网络模型效果出众，因此本文选择AlexNet作为基础模型进行改进。

3.3 板形模式识别的基本模式

板形缺陷识别就是判断板材中存在的缺陷类型，而板形缺陷种类繁多且有单一和复合型缺陷之分。生活中常见的板形缺陷模式有左边浪、右边浪、中间浪、双边浪、四分浪和边中浪［10］。如图3所示。

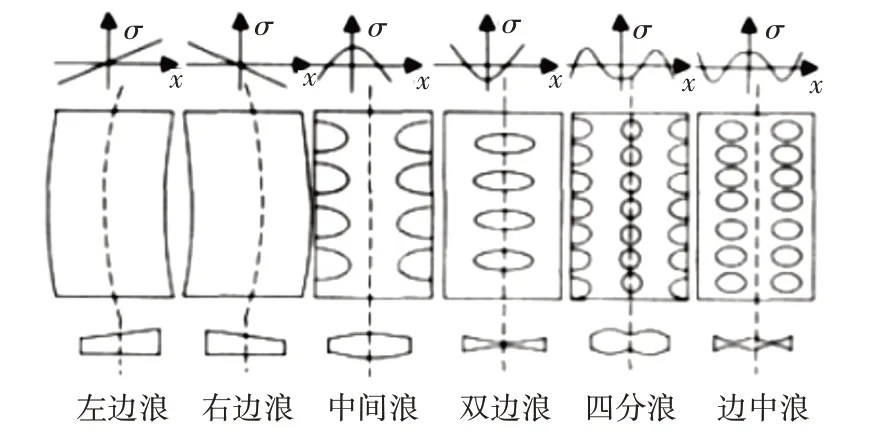
图3 6种板形缺陷模式

勒让德多项式为判断板形模式的常用方法，因为目前板形内部的残余应力用勒让德多项式表达最为准确［10］。几种常见的板形缺陷归一化方程如式（9）~（14）所示：

左边浪：

右边浪：

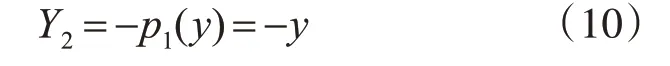
中间浪：

双边浪：

四分浪：

边中浪：

4 基于卷积神经网络的板形缺陷识别

4.1 双立方插值算法

因为数据集中的图片采集自不同的环境、设备，例如光照、拍摄角度等因素，所以极容易对图片产生干扰噪声，因此需要对图片进行预处理。

本文使用双立方插值算法对数据集中的图片进行尺寸的统一。其算法函数公式为

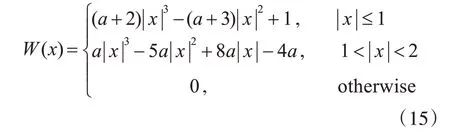
取a=-0.5，即：

假设原图片大小为m×n，像素坐标为(x，y)，目标图片大小为M×N，目标图片的像素坐标为( X，Y)，转换成原图片像素坐标为( x+μ，y+ν)：

双立方插值算法考虑参考点周围的灰度值变化，在图像缩放过程中可以更多地保留图像的细节，且放大后的图像不会带有锯齿。

本文另选择最近邻插值算法、线性插值算法与双立方插值算法进行比较，效果均不如双立方插值算法。最近邻插值算法采集的信息过于片面，只采集最近的信息，没有考虑周围信息的影响，尽管算法的速度较快但处理后的图片连续性不强，断层现象严重。线性插值算法虽然图片的连续性相较前者增强，但在图像边缘会出现模糊问题。因此本文对图片的预处理选择双立方插值算法。

4.2 板形缺陷识别模型（OP-AlexNet）网络结构设计

本文采用传统的AlexNet模型作为基础实验，在此基础上对AlexNet模型结构进行改进，因为本文数据集中的图片尺寸偏小，原结构的卷积核大小并不适用于处理本文数据集中的图片，为了更好地提取板形特征，本文将卷积核调小并只保留3层卷积层，卷积核大小分别为5×5，3×3，5×5。由于本文数据集庞大且板形缺陷较为复杂，为避免参数过多使得整个网络复杂度偏高，本文在原结构基础上减少1层全连接层。此外，将原结构的LRN层用BN层代替，BN层的计算方法是先求出数据x的均值和方差，接着将每一层地数据标准化，引入两个变量γ和β，最后输出。具体操作步骤如式（18）~（21）所示。

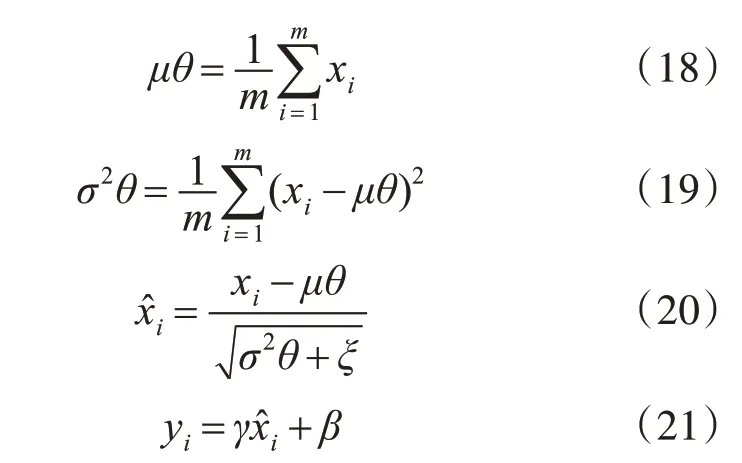
其中θ={ x1…m}，γ，β为待学习变量，xi为输入，yi为输出。因BN较LRN在数据处理上有着更好的包容性，因此在原结构上使用BN层代替LRN层。

综上，改进后的网络模型减少了训练时间，对图片特征提取的能力增强，使网络能够更好地适于板形缺陷识别。如图4所示为改进后的网络结构。

图4 OP-AlexNet模型网络结构

5 实验与结果分析

5.1 实验环境以及数据集

本文使用PyCharm2019.3.1实现板形缺陷识别系统，并进行实验，同时所使用的系统参数如表1所示。

表1 系统参数表

本实验选择kaggle比赛中的板材缺陷检测竞赛的实验数据作为板形缺陷识别模型的原始数据，以此来验证所提出模型的有效性。实验数据集中每一张图片都是带有缺陷的板材。图片共18074张，按照2∶1的比例划分，12050张为训练集，6024张为测试集。

5.2 实验过程

5.2.1 模型效果验证

本文实验在PyCharm2019.3.1中进行，首先按照前一节所述搭建好板形缺陷识别模型（OP-AlexNet），然后将图片输入进行训练实验。为了验证模型的性能，本文选择AlexNet做基础实验，并将两者的实验结果进行对比。每迭代100次记录当前验证精度，由此得到迭代次数与验证精度变化曲线图如图5所示。

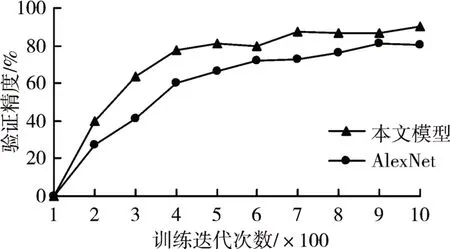
图5 AlexNet与板形缺陷识别模型验证精度对比

从图5中可以看出，在训练初期，两种模型的验证精度都存在波动，这是因为初始化权重不同对训练结果的影响较大。随着训练的进行，两种模型的验证精度都在提高并趋于稳定，收敛速度也在提高。但板形缺陷识别模型较经典AlexNet神经网络模型识别精度提高16.2%，并且收敛速度和鲁棒性都有了提升。

5.2.2 激活函数的改进对模型效果的影响

本文在OP-AlexNet模型基础上采用LeakyRe-LU激活函数与原本的ReLU激活函数进行对比实验，对比结果如图6所示。

图6 不同激活函数验证精度对比

由图可以看出，两种模型在迭代1000次后均已基本收敛，改进后的模型相较传统的AlexNet模型在验证精度上提高了1.25%。这是因为ReLU激活函数在作用时可能导致一部分神经元静默，从而导致这部分参数更新停滞。而LeakyReLU可以改善这个问题，因为LeakyReLU在负半轴不会出现导数为0的情况，可以使得这些被静默的神经元重新被激活，因此本文激活函数采用LeakyReLU。

5.3 实验结果分析

本文使用4.1节配置的实验环境进行训练，结束训练的迭代次数设置为1000次，本文统计了6种板形缺陷的识别精度、召回率和F1值来评价模型的性能，实验结果如表2所示。

表2 模型性能评价

从表2可以看出，左边浪和右边浪的识别效果最好，中间浪和双边浪的识别效果次之，四边浪和边中浪的识别效果较差。原因在于它们分别属于一次、二次和四次板形［10］，缺陷复杂度依次增高，识别的困难程度依次增大，因此识别效果依次降低。

为了使实验结果更具有说服力，将本文模型与未经预训练的VGGNet模型和Inception模型进行对比，并统计实验进行至1000次的精度变化。对比结果如表3和图6所示。

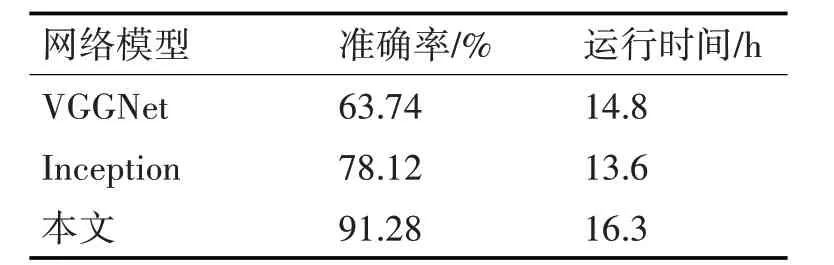
表3 不同模型性能对比

由图7可以看出，VGGNet和Inception模型的运行时间分别为14.8h和13.6h，本文模型在迭代1000次时的时间约为16.3h，分别是VGGnet和Inception模型的1.1倍和1.2倍。这主要是因为板形缺陷较为复杂导致参数过多，计算量较大，因而达到相同迭代次数的时间较长。然而本文实验模型准确率达到了91.3%，相较于VGGNet和Inception模型分别提高了27.5%和13.2%。VGGNet模型因其网络的深度与广度不高，随着迭代次数地增加效果会变差，错误率会提高。而Inception属于大型的深度提取网络，对数据集有着较为严格的标准，而本文的数据集还存在一定不足，因为实验结果较差。

图7 不同模型验证精度对比

6 结语

本文针对现有的板形缺陷识别操作复杂、成本高等问题，采用双立法插值算法统一数据集中的图片尺寸，以AlexNet为基础对网络模型结构进行改进，使其特征提取能力增强，并使用LeakyReLU激活函数替换ReLU激活函数对抑制的神经元进行重新激活，提出了OP-AlexNet模型。本文模型的识别准确率最终达到91.3%。相较传统的AlexNet模型提高了16.2%，相较于VGGNet和Inception模型分别提高了27.5%和13.2%，由此验证了该模型的有效性。但该模型相较于现有模型，训练时间相对较长，今后还需继续研究，缩短训练时间，以适应现代化工业生产。