Ocean Response to a Climate Change Heat-Flux Perturbation in an Ocean Model and Its Corresponding Coupled Model
Jiangbo JIN, Xiao DONG, Juanxiong HE, Yi YU, Hailong LIU, Minghua ZHANG, Qingcun ZENG,He ZHANG, Xin GAO, Guangqing ZHOU, and Yaqi WANG
1International Center for climate and Environment Sciences (ICCES), Institute of Atmospheric Physics,Chinese Academy of Sciences, Beijing 100049, China
2State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography,Ministry of Natural Resources, Hangzhou 310012, China
3State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics (LASG),Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100049, China
4College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
5School of Marine and Atmospheric Sciences, Stony Brook University, Stony Brook, New York, NY 11790, USA
(Received 4 May 2021; revised 11 August 2021; accepted 17 August 2021)
ABSTRACT State-of-the-art coupled general circulation models (CGCMs) are used to predict ocean heat uptake (OHU) and sealevel change under global warming. However, the projections of different models vary, resulting in high uncertainty. Much of the inter-model spread is driven by responses to surface heat perturbations. This study mainly focuses on the response of the ocean to a surface heat flux perturbation F, as prescribed by the Flux-Anomaly-Forced Model Intercomparison Project(FAFMIP). The results of ocean model were compared with those of a CGCM with the same ocean component. On the global scale, the changes in global mean temperature, ocean heat content (OHC), and steric sea level (SSL) simulated in the OGCM are generally consistent with CGCM simulations. Differences in changes in ocean temperature, OHC, and SSL between the two models primarily occur in the Arctic and Atlantic Oceans (AA) and the Southern Ocean (SO) basins. In addition to the differences in surface heat flux anomalies between the two models, differences in heat exchange between basins also play an important role in the inconsistencies in ocean climate changes in the AA and SO basins. These discrepancies are largely due to both the larger initial value and the greater weakening change of the Atlantic meridional overturning circulation (AMOC) in CGCM. The greater weakening of the AMOC in the CGCM is associated with the atmosphere-ocean feedback and the lack of a restoring salinity boundary condition. Furthermore, differences in surface salinity boundary conditions between the two models contribute to discrepancies in SSL changes.
Key words: ocean heat uptake, Atlantic meridional overturning circulation, ocean general circulation model, coupled general circulation model
1. Introduction
Ocean heat uptake (OHU), which refers to the change in ocean heat content (OHC), leads to the thermal expansion of seawater and thus contributes to sea level rise (Kuhlbrodt and Gregory, 2012; Church et al., 2013). However,gaps in observational data in the deep ocean and the Southern Ocean (SO) make it difficult to estimate OHU (Garuba and Klinger, 2016). Therefore, atmosphere-ocean coupled models are widely used to investigate ocean climate changes (including changes in OHC, sea level, and ocean circulation) in response to increases in anthropogenic CO2.Increases in atmospheric CO2result in perturbations in heat,freshwater, and momentum fluxes at the oceanic surface,which can further cause changes to OHC through both thermodynamic and dynamic processes (Rahmstorf and Ganapolski, 1999; Gregory et al., 2005, 2016; Bouttes and Gregory,2014).
Recently, Huber and Zanna (2017) showed that perturbations in surface flux are major sources of spread among model estimates of OHU, especially surface heat flux perturbations. To reduce errors resulting from coupled models in the simulation and projection of OHU and sea-level rise in response to a doubled CO2concentration, the Coupled Model Intercomparison Project Phase 6 (CMIP6) launched the Flux-Anomaly-Forced Model Intercomparison Project(FAFMIP) to compare the responses of different models to the same surface flux perturbations (Gregory et al., 2016).Surface flux perturbations (including surface heat, freshwater, and momentum perturbations) in FAFMIP are derived from the ensemble mean differences between years 61 and 80 of the 13 CMIP5 atmosphere-ocean coupled models of a 1pctCO2 scenario experiments (corresponding to doubled CO2concentration) and from all years of piControl simulations and fixed seasonal cycles. FAFMIP experiments can be carried out with both Coupled General Circulation Models (CGCMs) and stand-alone Ocean General Circulation Models (OGCMs). However, few papers have focused on differences in results between OGCMs and CGCMs besides Todd et al. (2020).
Stand-alone OGCMs have been employed in the past to investigate ocean climate changes in response to increases in atmospheric CO2. Xie and Vallis (2012) used a simplified OGCM to show the importance of the redistributive effect of heat due to the weakening of the Atlantic Meridional Overturning Circulation (AMOC) in determining the spatial pattern of OHU. Garuba and Klinger (2016) designed different methods to isolate and quantify the contribution of the redistributive component to the total amount of OHU in a stand-alone ocean model. They found that most of the heat uptake in the North Atlantic is due to the weakening of the AMOC. Garuba and Klinger (2018) used an ocean model to isolate the impacts of each surface flux perturbation (including the heat flux, wind stress, and freshwater) on the OHU.Their model assumes that the total ocean circulation response due to all surface flux perturbations can be regarded as the sum of changes caused by each surface perturbation. Marshall et al. (2014) employed an OGCM to show that changes in surface temperature due to global warming in a simplified ocean-only model are similar to the ensemble mean changes of 15 coupled climate models from CMIP5. All of the experiments above show similar results to those reported by FAFMIP (Gregory et al., 2016), but they used different methods to separate the effect of the ocean dynamics and different forcing fluxes at the surface.Therefore, it is also necessary to understand the similarities and differences in FAFMIP experiments between OGCM and CGCM simulations in the projections of ocean climate changes. Previous studies have shown that ocean climate changes in response to CO2forcing are primarily determined by the uptake of surface heat flux perturbations(Garuba and Klinger, 2018; Gregory et al., 2016; Jin et al.,2021). Furthermore, much of the inter-model spread is also driven by the response to surface heat perturbations (Todd et al., 2020). Therefore, in this study, we investigated the similarities and differences in the projections of ocean climate changes between coupled and uncoupled models by using the FAFMIP heat flux perturbation experimental protocol and dataset. To quantify the contribution of ocean circulation, the decomposition method of Gregory et al. (2016)was adopted.
The paper proceeds as follows. The methods and experimental design are described in section 2. The results are presented in section 3, followed by a summary and discussions in section 4.
2. Models, experiments, and methods
2.1. Models
The simulations in this paper were performed using a stand-alone OGCM and a CGCM with the same oceanic component. Here, the OGCM is the second revised version of the LASG/IAP (State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics/Institute of Atmospheric Physics) Climate System Ocean Model (LICOM2.0) (Liu et al., 2012; Dong et al.,2021a). The model domain is global with approximately 1°horizontal resolution, with a 0.5° meridional resolution between 10°S and 10°N. There are 30 levels in the vertical direction, with 10 m per layer in the upper 150 m. The second-order vertical turbulent mixing scheme is applied(Canuto et al., 2001, 2002). The scheme of Gent and Mc-Williams (1990), which uses a diffusion coefficient of 1000 m2s-1for both the bolus and Redi parts, is used for the isopycnal mixing. Convection is parameterized by convective adjustment (Pacanowski, 1995). The sea surface salinity boundary condition in the OGCM is the combination of new well-posed boundary conditions (Jin et al., 2017) and restoring boundary conditions. This well-posed boundary condition uses the virtual salt flux that includes the proper correlations between the freshwater flux Fw and sea surface salinity, and the real salt flux is generally parameterized through 10-m wind speedU10,which can conserve total ocean salinity, the details can be found in Jin et al. (2017). Here, the sea-ice concentration is prescribed by its observed value from the National Snow and Ice Data Center (NSIDC)(Walsh et al., 2015).
The CGCM is the current version of the Chinese Academy of Sciences’ Earth System Model (CAS-ESM),which consists of IAP4.0 (Zhang et al., 2013) for the atmosphere, revised LICOM2.0 for the ocean, CoLM ((Dai et al.,2004; Ji et al., 2014) for the land surface, and CICE4.0(Hunke and Lipscomb, 2008) for sea ice. The atmospheric model uses a finite-difference scheme with a terrain-following coordinate and a latitude-longitude grid with a horizontal resolution of 1.4° × 1.4°. Arakawa’s staggered C grid is used for horizontal discretization. Furthermore, the top of the atmospheric model is about 2.2 hPa, and there are 30 layers in the vertical. CoLM and CICE4.0 share the same horizontal grid as the atmospheric and ocean models, respectively. The ecosystem and chemistry of CAS-ESM are closed in our study. A series of CAS-ESM versions (including its predecessor and component models) have been widely adopted in previous studies and applications, including, atmospheric circulation in middle-to-high latitudes(Dong et al., 2014), decadal variations of the East Asian summer monsoon (Dong and Xue, 2016; Lin et al., 2016),ENSO (Su et al., 2015), ocean assimilation in a coupled model framework (Dong et al., 2016, 2021b; Du et al.,2020), and short-term climate predictions for China (Lin et al., 2019). Although CAS-ESM is a newcomer in the community, since this is the first time that it is contributing to CMIP6 simulations, it has a good ability to reproduce the basic performances of the radiation budget of the atmosphere and ocean, precipitation, circulations, variabilities,the twentieth-century warming, and so on (Zhang et al.,2020).
2.2. Experiments
We designed two groups of experiments, one used the stand-alone revised LICOM2.0, and the other used CASESM. Each group included two experiments, one control and one perturbation experiment. For the control experiments, the OGCM and CGCM was spun up to reach a quasi-equilibrium state. For the OGCM, the Coordinated Ocean-ice Reference Experiments-I (CORE I) protocol proposed by Griffies et al. (2009) was employed, the repeating annual cycle of atmospheric forcing from Large and Yeager(2004) was used, and the model was spun up for 300 years.For the CGCM, the model was integrated for 1000 years under the pre-industrial scenario. Two additional 100-year simulations for both the coupled and uncoupled models were conducted by using the spin-up experiments as initial conditions. The OGCM and CGCM experiments are called OCTRL and CCTRL, respectively, and are listed in Table 1.
For the two perturbation simulations, both experiments started from the quasi-equilibrium state of the spin-up experiments, but the prescribed surface heat flux perturbation (F)of FAFMIP was bilinearly interpolated onto the OGCM's native grid and added to the sea surface heat flux which was used to calculate the temperature equation, which is from one of the FAFMIP experiments (denoted by FAF-heat in FAFMIP). Bilinear interpolation has been adopted in FAFMIP experiments (Todd et al., 2020).Fwas not directly applied to the sea-ice heat budget in order to eliminate the effects of sea ice. The turbulent heat fluxes for both the OGCM and CGCM were computed using the same bulk formulae. All other settings were the same as their control runs. We refer to the two OGCM and CGCM perturbation experiments as “OExp1” and “CExp1” in Table 1, respectively. To calculate the mean values for the basins, the ocean was divided into three parts: the Indo-Pacific Ocean (IP,22°-134°E and 35°S-65°N), the Arctic and Atlantic Ocean(AA, 35°S-90°N). and the Southern Ocean (SO,78°S-35°N).
Table 1. The configurations and the global mean values of ocean temperature anomaly (T′ ) , the added temperature change (), and the redistributive temperature anomaly ( for all OGCM and CGCM experiments, as well as changes in the maximum AMOC transport.

Table 1. The configurations and the global mean values of ocean temperature anomaly (T′ ) , the added temperature change (), and the redistributive temperature anomaly ( for all OGCM and CGCM experiments, as well as changes in the maximum AMOC transport.
?
2.3. Passive tracer method
Here, the passive tracer approach recommended by FAFMIP was adopted to separate the contributions of changes in ocean circulation and anomalous surface heat flux from temperature (Gregory et al., 2016). This method divides the temperature change into the added and redistributed components in the perturbation experiments.
In the following, the subscripts “c” and “p” denote values in the control and perturbation experiments, respectively, and primes denote the difference between the perturbation experiment and the control. The temperature equation for the control experiment can be schematically expressed as follows:

The equation sets the volumetric heat capacity to unity for convenience.Qcis the surface heat flux and applies only to the ocean surface, and ∇·(vcTc)represents all heat transport processes in the ocean, including large-scale and eddyinduced advection, diffusion due to sub-grid processes and deep convection, etc.
For perturbation experiments, the corresponding equa-tion for the temperature change with the addition of heat flux (F) and atmosphere-ocean heat fluxQpis as follows:

A passive tracerTris introduced and used to calculateQpin order to maximize the effect ofFon the sea surface.Tris not forced by the heat flux perturbationFand is only affected by changes in velocities and diffusivities due to the effects ofF. The seawater density is computed usingTpinstead ofTr, which means that the change inTrcannot affect ocean circulation. The equation for the passive tracerTris as follows:

TpandTrare both initialized toTc, so we can writeTp= Tc+T′ andandvpare split intoandvp=vc+v′, respectively.
According to the above decomposition, the equation for the temperature anomaly can be derived through Eqs. (1)and (2) as follows:
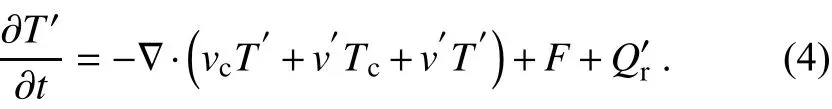
The difference betweenTcandTris the temperature anomaly due to the circulation changev′and redistributed heat flux anomalywhich is defined as the redistributive temperature anomalyc an be derived according to Eq.(3) - Eq. (1):

According to previous studies (Garuba and Klinger,2016, 2018), we can attribute the added temperature anomalyto the absorption of the prescribed perturbation in surface heat fluxF, which can be obtained by Eqs. (4) - (5).The corresponding equation is as follows:

Thus, the redistributive temperature perturbationmainly results from both the redistributed transport term (v′Tc) due to the circulation change and the initial current (or background current) transport termdue to the redistributive temperature change on the right side of Eq. (5).The added heat anomaly mainly results from the initial current transport termdue to added heat temperature change on the right side of Eq. (6). The total temperature anomaly can be regarded as the sum of the redistributive temperature anomalyand the added heat anomalywhich are the focus of the present study.
3. Results
The surface heat flux perturbation plays a predominant role in the weakening of the AMOC and increases the OHU among surface flux perturbations (Rahmstorf and Ganapolski, 1999; Gregory et al., 2005, 2016; Bouttes and Gregory,2014). Figure 1 shows the patterns of the prescribed surface heat flux anomalyFand the redistributed heat flux anomalyduring the final decade of both the OGCM and CGCM. The evident heating of the surface heat flux anomalyFprimarily occurs in the North Atlantic and the SO(Figs. 1a and 1c). The values ofFare almost identical between the OGCM and CGCM, and the ocean areal meanFin both simulations are 1.87 W m-2and 1.81 W m-2,which is consistent with the value (1.86 W m-2) provided by Gregory et al. (2016). In the OGCM,Fexhibits slightly more heat input in the Labrador Sea and Bering Strait (Fig.1e), which is caused by a greater concentration of sea ice in the OGCM compared to that in the CGCM. The sea ice concentration in the OGCM is a prescribed observation and uses simulated values by the sea-ice model CICE4.0 in the CGCM.
Q′r A predominant feature of in both simulations is that it is relatively large and positive in the North Atlantic and negative in the low latitudes of the Atlantic (Figs. 1b and 1d),which is related to the weakening of the AMOC due to the heat flux perturbation,F.Due to strong positive feedback,the AMOC weakening leads to the cooling of redistributed sea surface temperature (SSTr), the freshening of the sea surface salinity in the North Atlantic, and SSTr warming in the low latitudes of the Atlantic due to a reduced northward transport of warm and salty water, which enhances the local heat input to the North Atlantic and further exaggerates the weakening of the AMOC.

Fig. 1. The prescribed heat flux anomaly (F) from FAFMIP for (a) OExp1, (c) CExp1, and (e) their differences(OExp1 - CExp1). (b), (d), (f), describe the same results as (a), (c), (e), but for the heat flux anomaly due to the redistribution of the SST () (units: W m-2), the positive value indicates downward.

Fig. 2. The Atlantic Meridional Overturning Circulation (AMOC) for the OGCM (a) control run (OCTRL), (b)perturbation run (OExp1), and (c) their difference (OExp1 - OCTRL). (d), (e), (f), show the same results as (a), (b), (c),but for CGCM (units: Sv).
The simulated AMOC, ocean heat content, and sealevel change which are essential measures in predicting future climate change, are discussed in the following. The prescribed heat flux perturbation,F, into the Atlantic mainly occurs in the North Atlantic region, which enhances the ocean stratification stability, and the subsequent reduction in subduction results in the weakening of AMOC.Figure 2 shows the AMOC and its changes for the OGCM and CGCM. In both the OGCM and CGCM, the AMOC declines in response to the imposed heat flux anomaly,F.Compared with the OGCM, the stronger initial AMOC and larger reduction in transport due to warming in the coupled model leads to greater cooling in the Atlantic (Fig. 2, Winton et al., 2013), which can explain the difference in the redistributed heat flux anomalyin the AA between the OGCM and CGCM. The corresponding maximum values of the AMOC simulated in the CCTRL and OCTRL are 19.7 Sv and 13.2 Sv, respectively, while changes in the maximum AMOC for the OGCM and CGCM are 7.3 Sv and 8.5 Sv (Figs. 2c and 2f). The larger reduction in the AMOC in the CGCM is consistent with the results of Todd et al.(2020). This difference is largely due to lower salinity in the North Atlantic in the CGCM relative to that in the OGCM(Fig. S2) since the OGCM combines the restoring and wellposed salinity boundary conditions, and the CGCM only uses the well-posed salinity boundary condition.


The large discrepancies between the OGCM and CGCM occurring in the AA basin are also due to the redistributed temperatureFigs. 3g-i), as reflected in the basin mean values and OHU. The large positive values can be found in the Gulf Stream region and South Atlantic. Compared with the OGCM, the stronger initial AMOC and larger reduction in transport in the coupled model leads to stronger cooling in the Atlantic (Fig. 4, Winton et al., 2013).This can explain the difference in the redistributed heat flux anomaly in the AA between the OGCM and CGCM.

Fig. 3. The total ocean heat content change due to (a) the ocean temperature anomaly (T), (b) added temperature change (),and (c) the redistributive temperature anomaly () during the final decade of the experiments for OGCM. (d,) (e), (f), show the same results as (a), (b), (c), but for CGCM. (g), (h), (i), are the differences in T′, between the OGCM and CGCM, respectively (units: 109 J m-2).
Long-term variations are fundamental metrics for assessing the performance of the model. Figure 4 shows the time seriesofthemeanoceantemperatureanomalyT′,andatthe global and basinscalessimulatedby boththe OGCM and CGCM. The temperature changes show a similar linear rising trend in both experiments. The warming trends are mainly caused by the added heat anomaly,which contributes to approximately 90% of the increase inT′, while the contribution ofis about 10%.
The global mean temperature changeT’for the OGCM is about 5% greater than that for the CGCM (Fig. 4a). The values of global meanT′in the 100th year for the OGCM and CGCM are 0.443°C and 0.419°C, respectively (Table 1).The added and redistributed heat tracers both have positive contributions to the difference inT′between the OGCM and CGCM (Fig. 4a): 0.015°C (0.386°C - 0.371°C) and 0.009°C(0.057°C - 0.048°C), respectively (Table 1). Similar to the temperature change, the OHU (24.1 × 1023J,in the OGCM is also slightly larger than that (22.8 × 1023J)in the CGCM (Table 2). In general, the differences inT′and OHU between the two models are attributed more toFand heatinputsofFandare21.0 ×1023Jand3.1×1023Jininthe OGCMthanthose in theCGCM(Fig.5a). The the OGCM and 20.2 × 1023J and 2.6 × 1023J in the CGCM,respectively (Table 2). In addition, the magnitude of interannual variability in surface heat fluxes for the CGCM is much larger than that for the OGCM due to the stronger intrinsic variability, but we do not discuss this issue here.

Fig. 4. The global and basin mean changes in ocean temperature anomaly (T), added temperature change (), and redistributive temperature anomaly () simulated by the OGCM and CGCM for (a) global, (b) the Indo-Pacific (IP),(c) the Arctic-Atlantic (AA), and (d) Southern (SO) Oceans (units: °C).

Table2.Time-integratedtotal surfaceheat flux anomaly?,prescribed heat fluxanomaly(F), redistributedheatfluxanomaly ?andOHU?addedOHUa ?andredistributedOHUr ?inthe OGCMand CGCMexperiments.
The basin heat flux anomaly input and the tendency of OHU are not balanced, which is mainly because of the heat exchange between the basins, especially between the AA and SO. For instance, in the SO, the prescribed heat flux,F,in the OGCM is almost the same as that in the CGCM, and the redistributed heatinput (0.2 × 1023J) in the OGCM is larger than that (-0.9 × 1023J) in the CGCM (Fig. 5d and Table 2). The basin meanand OHUa for the SO in the OGCM is larger than that in the CGCM, and the basin meanand OHUr in the OGCM are less than that in the CGCM(Fig. 4d and Table 2). The former is mainly related to a greater change in northward meridional heat transport for(the main contributor to theterm; see Eq. 6) in the CGCM (2.0 × 1023J) than that in the OGCM (1.3 × 1023J),which is due to the larger initial strength of the AMOC in the CCTRL (Fig. 2d), and the latter is largely a result of a greater change in southward meridional heat transport from the AA to SO in the CGCM (main contributor to thecterm) due to a larger reduction in the AMOC (Table 3).
Table 3. Time-integrated meridional heat transport of total temperature change (T′), redistributed temperature change (), and added temperature change () simulated by the OGCM and CGCM. A positive value denotes northward meridional heat transport (MHT).

Table 3. Time-integrated meridional heat transport of total temperature change (T′), redistributed temperature change (), and added temperature change () simulated by the OGCM and CGCM. A positive value denotes northward meridional heat transport (MHT).
?
We further examined the effects of thermal expansion on sea-level rise. Here, the spatial distribution of the changes in the SSL [steric sea level,the TSSL [thermosteric sea level,and the HSSL [halosteric sea level,for the OGCM and CGCM, as well as their differences, are shown in Fig. 6. Similar to the spatial pattern of changes in the vertically integrated OHC, the spatial patterns of changes in SSL, TSSL,and HSSL are also almost similar between the two models.The changes in SSL in both models are mainly determined by the change in TSSL. HSSL is of regional importance in the AA and SO basins. Compared to the CGCM, a larger rise in TSSL in the OGCM is observed in the Gulf Stream region and South Atlantic, which are similar to the difference in the vertically integrated OHC change between the two models. The discrepancies between the OGCM and CGCM occur in the AA and SO basins due to the combined effects of TSSL and HSSL (Figs. 6g-i). The difference in HSSL in the Arctic Ocean and SO between the OGCM and CGCM are also mainly due to the different sea salinity boundary conditions between the two models.

Fig. 5. The global and the basin means time series of the heat flux anomaly (F) from FAFMIP, the heat flux anomalyresulting from the redistribution of SST and the total surface heat flux anomaly (F + simulated by the OGCM and CGCM for the (a) global, (b) the Indo-Pacific (IP), (c) the Arctic-Atlantic (AA), and (d) the Southern(SO) Oceans (units: W m-2).
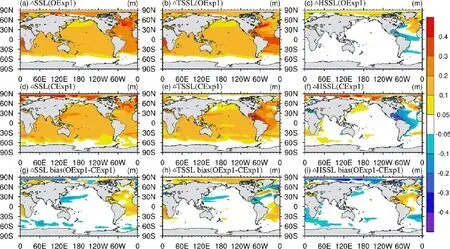
Fig.6. Thespatialdistributionof changesinSSL[stericsealevel, for(a)OGCM,(d)CGCM, and(g) theirdifferences(OGCM -CGCM);(b), (e), (h), and(c), (f),(i),showthesame results as(a),(d),(g),but forTSSL [thermosteric sea level, and HSSL[halostericsealevel,
4. Summary and discussion
In this study, the differences in the simulated response to global warming between a stand-alone ocean model and a fully-coupled model were investigated using heat flux anomaly experiments according to the FAFMIP protocol(Gregory et al., 2016). We found that global mean warming trends are mainly caused by anomalous surface heating (F)which contributes approximately 90% to the increase inT′.An important finding is that the global mean temperature changes (T’,and), ocean heat content changes (OHU,OHUa, and OHUr), and the spatial patterns of SSL and TSSL changes are generally consistent between the standalone OGCM and CGCM simulations, indicating that the ocean model alone can also be used to approximate ocean heat uptake processes and changes in SSL.
This study also reveals slight differences in ocean climate changes between the OGCM and CGCM. For the global mean variables, the magnitudes of the global temperature changeT′and OHU in the OGCM are about 5% greater than those in the CGCM, which is the result of the combined effect of the added temperature changedue to the added heat flux perturbation (F) and the redistributed temperaturechangedue totheredistributedheatfluxanomaly.Alargerweakeningof theAMOCoccurredinthe CGCM which was largely attributed to lower salinity values in the North Atlantic relative to that in the OGCM, this is because the restoring salinity boundary condition is applied in the OGCM and absent in the CGCM. Consistent with previous studies (Gregory et al., 2016), we found that the greater AMOC weakening in coupled models causes an increased input from the redistributed heat flux anomalyin the AA region compared to stand-alone models.However, the global meanin the coupled model is lower than that in the OGCM; this difference is attributed to a lack of air-sea interaction in the OGCM because the shortwave flux and surface air temperature are prescribed in the standalone model and simulated by AGCM in the CGCM (Fig. S1 in the ESM).
For the basin-scale results, we find that for the IP basin,the mean temperature and ocean heat content changes in the OGCM are almost identical to those in the CGCM. In contrast, there is a warmer basin mean temperature changeT′and a larger OHU in the SO and AA in the OGCM relative to those in the CGCM. The smaller changes in added heat temperatureand the OHUa of the SO in the CGCM are largely due to the initial greater strength of the AMOC,which exhibits a greater northward meridional heat transport forfrom the SO to AA. The differences inin the SO and AA between the two models are mainly due to the different degrees of weakening of the AMOC in response to global warming. Since the greater weakening of the AMOC is accompanied by a larger North Atlantic SST cooling in a CGCM, it will have the effect of not only amplifying theinput relative to the OGCM (especially for the North Atlantic) but will also provide for a greater southward meridional heat transport change from the AA to the SO. Besides,the atmosphere-ocean feedbacks that are present in CGCM and absent in OGCM tend to enhance the pattern of the North Atlantic OHC and TSSL changes, exhibiting relatively stronger increases in the tropics and decreases in the extratropics. The above processes are schematically described in Fig. 7.

Fig. 7. Diagram describing the difference in T′ (corresponding to OHU),(corresponding to OHUa), and(corresponding to OHUr) between the OGCM and CGCM. The figures show whether they exhibit warming(red) or cooling (blue) in the OGCM compared to CGCM. MHTa is the northward meridional heat transport for , and MHTr is the northward meridional heat transport for
Both the CGCM and OGCM show that the SSL is mainly determined by the change in TSSL. Changes in the TSSL and HSSL largely cancel out, but both terms contribute to the overall SSL change in the SO and AA basins. The main discrepancies in SSL between the CGCM and OGCM over the Atlantic and SO are due to differences in the HSSL change, which are also related to the difference in sea surface salinity boundary conditions between the models.
The SO is a key region for the absorption and storage of anthropogenic heat. This study only focused on the effects ofFregarding ocean climate change. While the SO ocean heat uptake is also closely related to the magnitudes of the wind and gyre boundary poleward shifts (Sen Gupta et al., 2009; Lyu et al., 2020), it is worth investigating what role the wind stress change plays in the ocean heat uptake and redistribution by analyzing wind stress perturbation experiments (FAF-stress) in FAFMIP.
In this study, we only compared the output from the OGCM and CGCM using one Earth system model (CASESM2) and its ocean component. Although the differences between the OGCM and CGCM are explained reasonably well, we cannot confirm whether the results are model dependent. FAFMIP provides an opportunity to investigate inter-model differences, such as Todd et al. (2020) who examined the ocean's response (especially for ocean heat uptake and dynamic sea-level change) to surface momentum and buoyancy flux perturbations provided by FAFMIP in an ensemble of five OGCMs and two CGCMs.Besides, more physical meaning should be considered, for instance, if climate models have a initially cold bias over the SO and are also accompanied by an eddy-driven jet equatorward bias in the mid-latitudes, and more cloud cover and sea ice, which tends to enhance the effects of global warming (Kajtar et al., 2021).
Finally, adopting method B of FAFMIP will result in the same order of magnitude for the calculatedand the prescribed heat flux perturbationF, in the North Atlantic,which means that the effect ofFis accounted for twice, resulting in a further reduction in AMOC intensity compared to the scenario of doubled CO2concentration. Currently, to eliminate the effects of the doubled contribution ofF,FAFMIP has provided a new experiment, in which the added heat flux perturbationF, is multiplied by 0.5 for part of the North Atlantic. The results of the new experiment and the calculation of heat flux in high-latitude regions in the North Atlantic remain issues that are worthy of investigation in the future.
Acknowledgements. The constructive suggestions and comments from the two anonymous reviewers and Editor are highly appreciated. This work is jointly supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA19020202), Key Research Program of Frontier Sciences,the Chinese Academy of Sciences (Grant No. ZDBS-LYDQC010), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB42000000) and the open fund of State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography (Grant No.QNHX2017). Xiao DONG was supported by the National Natural Science Foundation of China (Grant No. 41706028). The simulations were performed on the supercomputers provided by Earth System Science Numerical Simulator Facility (EarthLab).
Electronic supplementary material:Supplementary material is available in the online version of this article at https://doi.org/10.1007/s00376-021-1167-y.
 Advances in Atmospheric Sciences2022年1期
Advances in Atmospheric Sciences2022年1期
- Advances in Atmospheric Sciences的其它文章
- Erratum to: Implications from Subseasonal Prediction Skills of the Prolonged Heavy Snow Event over Southern China in Early 2008
- The Surface Energy Budget and Its Impact on the Freeze-thaw Processes of Active Layer in Permafrost Regions of the Qinghai-Tibetan Plateau
- Lightning Nowcasting with an Algorithm of Thunderstorm Tracking Based on Lightning Location Data over the Beijing Area
- Forecasting Zonda Wind Occurrence with Vertical Sounding Data
- Three-Dimensional Wind Field Retrieved from Dual-Doppler Radar Based on a Variational Method: Refinement of Vertical Velocity Estimates
- Atmospheric Disturbance Characteristics in the Lower-middle Stratosphere Inferred from Observations by the Round-Trip Intelligent Sounding System (RTISS) in China
