前体尾流对降落伞工作性能的影响
吴卓恒,余莉,2,*,赵晓舜,聂舜臣
(1.南京航空航天大学飞行器环境控制与生命保障工业和信息化部实验室,南京 210016;2.南京航空航天大学航空学院,南京 210016)
降落伞由于其良好的减速性能和稳定性能,被广泛用于各类飞行物体的减速回收。但是,在物伞系统的减速飞行过程中,降落伞均处于物体后面,前体尾流对降落伞的气动性能有极其重要的影响。为了减小前体尾流对伞衣气动性能的影响,在设计物伞系统结构时,通常需要将降落伞置于前体尾流区外。笔者将物伞的相对距离与前体直径的比值称为拖曳比。拖曳比过大虽然能克服尾流影响,但是会导致物伞系统质量增加、柔性加强、受环境影响加大。为了获得合适的拖曳比,需要对前体尾流开展深入的研究。
前体尾流对降落伞工作性能的影响一直都是国内外物伞系统设计的研究重点。一部分学者通过风洞试验开展研究,如Steinberg等[1]发现前体阻挡来流进入伞衣,随速度增加前体尾流区范围增大、动压减小,伞衣阻力损失也会随之增加。韩晋阳等[2]发现前置体的尾流效应会导致伞衣外形变化、伞衣收缩、投影直径减小从而导致阻力系数减小。还有一部分学者通过数值模拟开展研究,主要有2种思路:一种是计算流体力学(Computational Fluid Dynamics,CFD)方法,该方法主要对物伞系统的流场分布规律及伞衣气动特性进行研究,常用于伞衣外形变化不大的稳降阶段,如Sengupta等[3-5]对超声速降落伞进行CFD数值模拟,发现前体尾流改变了伞前激波形状,进入伞衣内的气流质量减少,伞衣阻力系数减小。贾贺等[6]发现伞前激波与前体亚音速尾流存在周期性的相互影响,在伞内高压区的作用下伞前激波逐渐向前推进与前体激波相融合,而前体尾流又会导致伞前激波的扩散不稳定。另一种思路是流固耦合(Fluid-Structure Interaction,FSI)方法,该方法反映了非定常流场和柔性伞衣相互作用机制[7-10],能直观得到前体尾流对伞衣的气动干扰情况,但数值模型复杂、耦合难度高和计算消耗大,通常用于外形变化比较剧烈的场合,如余莉和杨雪等[11-13]对超声速盘缝带伞进行了FSI数值研究,得到了以前体尾流和伞前激波为主的流场结构,分析了尾流作用下伞衣的激波振荡和呼吸现象。Lingard和Xue等[14-17]对超声速降落伞复杂的流场结构进行研究,发现前体尾流动压减小会造成伞衣阻力损失,影响伞衣充气过程的稳定性[15],拖曳比过小前体尾流对伞衣气动干扰强烈[16],伞衣出现严重的收缩现象[17]。上述工作从不同角度均发现前体尾流对降落伞存在或多或少的影响,但是并没有对前体尾涡结构及影响机制开展深入的研究。
本文基于Realizable k-ε湍流模型,采用PISO算法对稳降阶段的物伞系统进行了非定常数值模拟,研究了不同拖曳比下前体尾流对流场分布和旋涡演变的非定常影响,分析了不同拖曳比下降落伞气动特性的变化,为物伞系统的拖曳比设计提供一定参考。
1 数值计算方法
1.1 湍流模型及数值方法
在非定常计算中,湍流模型对流场结构(旋涡、压力等)的捕捉和计算精度的影响很大,k-ε两方程湍流模型被广泛用于壁面绕流问题,其中Standard k-ε湍流模型考虑了速度和湍动能长度比例尺的分布,具备较好的计算精度和计算效率,但是忽略了气流的黏性作用;Realizable k-ε模型增加了曲率和旋转的影响,计算消耗增加但提高了计算精度。为获得准确、精细的前体尾涡结构,本文基于Realizable k-ε湍流模型,采用标准壁面函数法(Standard Wall Functions)开展非定常绕流数值计算,湍流模型控制方程如下:


本文基于有限体积法采用MUSCL三阶格式进行流场方程离散,为了提高瞬态计算精度并加速收敛过程采用PISO算法,其中压力插值选择Standard格式,为了能有效处理非定常计算的伪扩散问题选择Green-Gauss Node-based进行梯度插值。边界条件采用速度进口和压力出口,采用了远场边界条件,伞衣面及前体为无滑移边界条件。
1.2 方法验证
为了验证本文方法的有效性,采用文献[18]中的平面圆形伞开展非定常数值计算。图1为伞衣平面结构,当伞衣面积Ac=40 m2、名义直径D0=7.1 m、伞顶孔直径Dd=0.4 m时,风洞试验得到该伞的阻力系数为0.82。
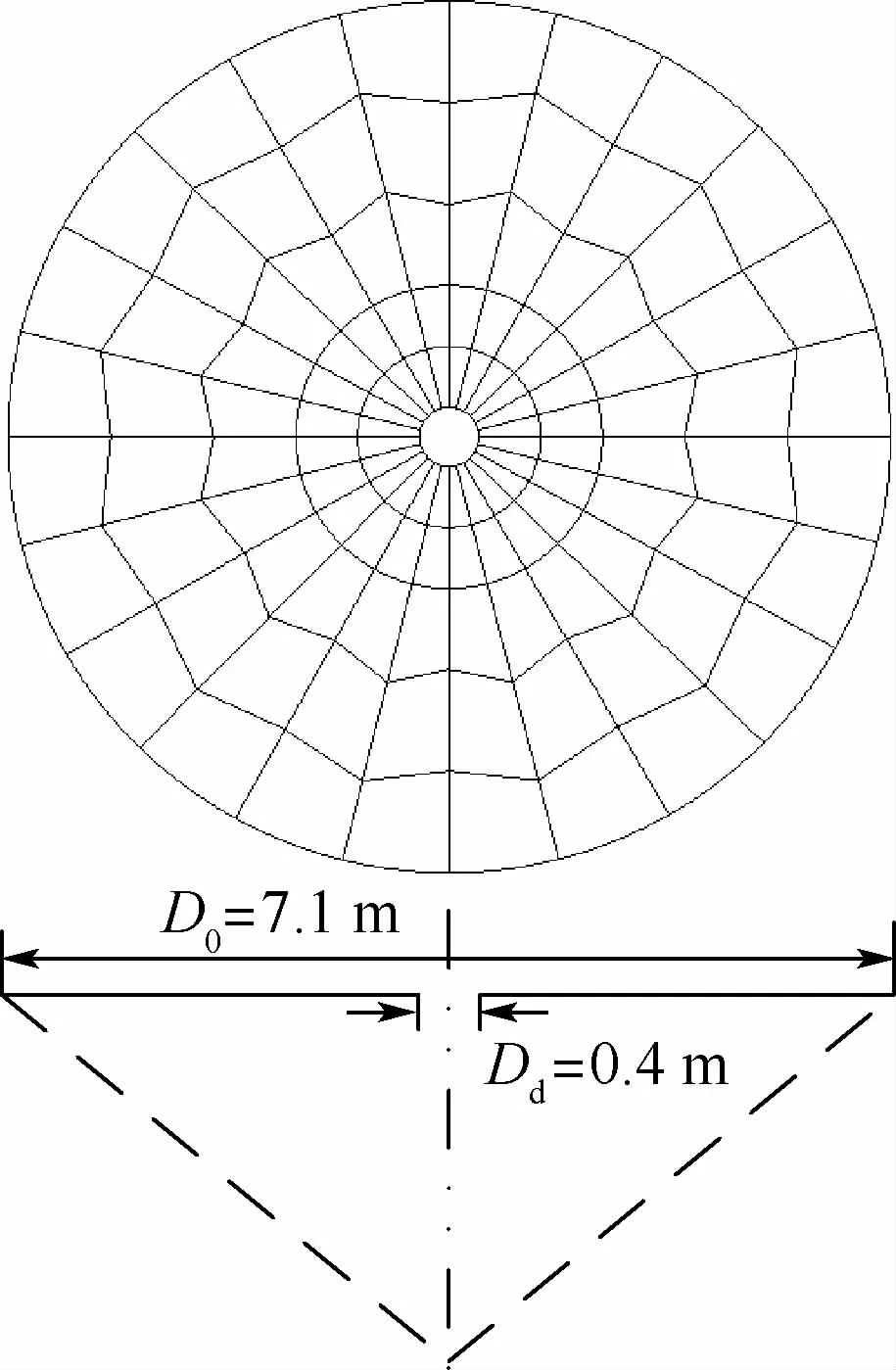
图1 伞衣平面结构参数[18]Fig.1 Planar structure parameters of canopy[18]
本文针对降落伞稳降阶段的非定常绕流流场展开数值研究,做如下假设:
1)不考虑前体和伞绳对流场的影响。
2)降落伞处于匀速稳定下降阶段,伞衣外形不变,不考虑伞衣织物透气性[19]。
3)伞衣充满外形为半球形,投影直径Dt和名义直径D0的比取经验值0.7[20]。
4)流场计算域为围绕伞衣轴对称的圆柱形,计算域直径为6 Dt、高为8.6 Dt。
根据上述假设,本文建立如图2所示的伞衣充满外形和流场网格模型,D、hj分别为伞衣充满下的伞顶孔直径、伞衣高度,其中,在伞衣附近及尾涡区进行了网格局部加密,以增加计算精度和捕捉尾涡细节,网格总数为121万。计算工况为:计算高度为H=400 m,来流速度v=15 m/s,大气压力p0=95 kPa。


图2 伞衣充满外形和计算网格Fig.2 Full shape of canopy and computational grid

图3 降落伞尾涡结构Fig.3 Parachute wake vortex structure

表1 数值计算结果Table 1 Numerical calculation results
2 研究对象及工况
本文针对1.2节的降落伞加附圆锥形前体,开展不同拖曳比下物伞系统的绕流流场计算,物伞系统三维模型如图4所示。前体直径d=2.4 m、高h=2.5 m;α为前体锥角;拖曳比λ分别取2、4、6、9、12;大气条件为离地高度H=200 m,来流速度v=15 m/s。

图4 物伞系统三维模型Fig.4 3-D model of capsule-parachute system
非定常固壁绕流问题中,网格对流场结构影响很大,为获得准确的尾涡结构变化,本文采用求解固壁绕流适应性好的三角形网格,同时对尾涡区的流场网格进行加密,物伞网格数为11 631个,流场网格数为143万个,数值模型如图5所示。

图5 物伞系统数值模型Fig.5 Numerical model of capsule-parachute system
3 计算结果及分析
3.1 旋涡演变分析
图6为计算稳定之后的流场旋涡分布。可以看出,在稳降阶段,前体和伞衣表面仍不断出现旋涡的生成与脱离,当λ≤6时,伞衣受前体尾涡影响严重,伞衣入口的涡量大小和方向时刻发生变化,这可能是造成伞衣摆动的重要原因;随着拖曳比增加,前体尾涡的黏性耗散增加、涡量逐渐减少,当λ≥9时,伞衣入口开始形成稳定的负涡量区,物伞系统的绕流流场相对稳定,前体尾涡对伞衣的影响逐渐减弱。

图6 流场旋涡演变规律Fig.6 Variation rule of flow field vortex


3.2 流场分布规律

图7 物伞尾涡脱离周期和平均涡核涡量Fig.7 Wake vortex departure period and average vorticity magnitude of capsule-parachute system

图8 伞衣入口处旋涡强度变化Fig.8 Variation of vorticity magnitude at the entrance of canopy
图9为不同拖曳比下趋于稳定时物伞系统的流场分布。可以看出,拖曳比改变着物伞系统的绕流流场分布,当拖曳比过小时(如λ=2),前体阻挡了自由来流进入伞衣,前体和伞衣形成闭式流动,流域P气流动压极低,伞衣阻力损失严重;随着拖曳比增加逐渐转变为开式流动,前体尾流区的压力和气流速度具备恢复的过程,物伞系统的流场速度分布和压力分布更为对称,伞衣底部形成稳定的正压区。

图9 物伞系统流场图(t=15 s)Fig.9 Flow field of capsule-parachute system(t=15 s)
为探究拖曳比对前体和伞衣附近流场影响的强弱,在对称轴前体后方0.5 m处(A点)和伞衣入口前方0.5 m处(B点)进行流场压力监测,得到2个特征点的压力变化情况(见图10)。从图中可以看出,稳定后前体尾流区前端(A点)的压力变化幅度远小于后端(B点),拖曳比对后端(B点)流场压力的影响远大于前端(A点)。随拖曳比增加,A点的流场压力逐渐减小,而伞衣入口B点的流场压力明显增大。当λ=2时,伞衣入口和前体后方流场压力的变化趋势和大小几乎一致,此时伞衣位于前体尾流负压区内,伞衣完全处于闭式流动中。

图10 流场压力变化Fig.10 Variation of flow field pressure
3.3 气动特性分析
图11为不同拖曳比下伞衣沿子午线上的内外压力及压强系数Cp分布。可以看出,伞衣完全处于闭式流动时(λ=2),伞衣内外侧压力大小接近,压强系数较小且存在负值的情况,降落伞正常的工作性能受到影响;而当伞衣处于开式流动时(λ≥2),伞衣内侧压力均明显大于外侧压力,具有较好的减速能力,随着拖曳比增加,伞衣内外侧压力和压强系数均逐渐增加,气动阻力增加;当λ≥9时,尾流对伞衣面压强系数的影响减小。

图11 伞衣沿子午线上的内外压力及压强系数分布Fig.11 Internal and external pressure and pressure intensity coefficient distribution along the meridian of canopy


图13 平均阻力系数随拖曳比的变化Fig.13 Variation of average drag coefficient with drag ratio

4 结 论
为研究前体尾流对降落伞工作性能的非定常影响,本文开展了不同拖曳比下物伞系统的数值研究,得出如下结论:
1)拖曳比对前体尾涡脱离周期几乎没有影响,但对伞衣影响很大。随拖曳比增加,前体尾涡到达伞衣入口处的时间增加,受涡量黏性耗散影响,进入伞衣的旋涡强度减弱,伞衣底部形成稳定负涡量区,伞衣尾涡脱离周期随之延长。
2)当拖曳比过小时,伞衣完全处于尾流区内,形成闭式流动。随着拖曳比增加逐渐转变为开式流动,物伞系统的流场速度和压力分布更为对称,伞衣底部形成稳定的正压区。
3)拖曳比对伞衣入口处流场压力的影响远大于前体后方。随拖曳比增加,稳定时的流场压力明显增加,伞衣内外压差增加,但当λ≥9时,前体尾流对降落伞阻力系数和伞衣面压强系数的影响减小。

