抗控制饱和的鲁棒非线性飞行控制方法
孙冰,陈伟
(1.吉林化工学院信息与控制工程学院,吉林 132022; 2.中国工程物理研究院总体工程研究所,绵阳 621900)
目前,飞行器的种类越来越多,某些类型飞行器可以胜任多种类型的飞行任务,具有较大的飞行包线范围,可在较大的速度、升限范围内执行飞行任务,甚至可进行高动态机动飞行。对于大部分飞行器来说,都是采用舵机作为执行机构控制其飞行姿态,舵面会受到物理偏转的限制,对于指令的精确跟踪十分不利,甚至会导致飞行控制闭环系统不稳定[1-2]。另外,对于螺旋桨类飞行器来说,其飞行动力由螺旋桨旋转提供,飞行器在加速和高机动飞行过程中,发动机的转速很可能会达到上限,该现象不仅会影响控制精度,而且会大大缩短发动机的使用寿命[3-4]。
针对该问题,大量学者开展了抗饱和控制方法研究[5-6]。吴跃飞等[7]针对火箭炮控制输入受限问题,将一种辅助分析系统与反步方法相结合,对自适应控制量进行相应的调整,并通过李雅普诺夫稳定性理论证明了所设计控制系统的稳定性。周洪波等[8]针对小型无人直升机状态受限问题,引入二阶滤波器对中间虚拟控制信号的幅值和变化速率进行限幅,对受限状态设计补偿系统,并证明了直升机补偿跟踪误差全局指数稳定。Herrmann等[9]针对一类输入受限可反馈线性化的非线性系统,设计了一种抗饱和补偿系统,Guillaume[10]将这种抗饱和补偿系统应用到一种小型无人机控制律设计中,有效地抑制了积分器的饱和。孙超娇等[11]针对多操纵面飞行器易陷入舵面饱和的问题,基于权系数空间优化,提出了2类最优抗饱和控制分配策略,仿真表明,该方法在保证控制精度的同时,较好地实现了抗饱和控制。成高等[12]针对再入飞行器,设计了一种在方向舵失效情况下的抗饱和姿态控制方法,结果表明,该方法在大迎角飞行造成偏航舵失效的情况下,具有良好的抗饱和姿态控制能力。
飞行器在进行高机动飞行过程中,纵向和横侧向相互耦合,各控制通道相互交联,导致其模型具有较强的时变性和不确定性,很难用精确的数学模型进行描述。本文将模型参数分为已知的标称模型参数和未知的建模误差两部分,建模误差和外界干扰合并称为模型不确定项,建立了某飞行器的严格反馈非线性模型[13]。鉴于自适应反步法能够充分利用非线性系统本身固有的非线性特性,在处理非线性问题时具有其独特的优越性,设计了一种抗饱和自适应反步非线性飞行控制方法。由径向基函数(RBF)网络对建模误差和外界干扰进行逼近。针对升降舵偏转和发动机转速受限问题,分别设计相应的抗饱和动态补偿系统,输出补偿信号对控制输入饱和起到抑制作用,可帮助系统在较短时间内脱离饱和,恢复到正常控制。仿真结果表明,所设计的飞行控制系统具有较高的鲁棒性,状态跟踪误差能够快速收敛。
1 纵向运动系统与问题描述
为了便于分析纵向运动,利用水平无侧滑飞行条件将某飞行器运动方程进行解耦,得到如下纵向运动方程[14]:

其中:Q为动压;Sw为机翼参考面积;δe为升降舵偏角;CL0为零迎角升力系数;CLα和CLδe分别为升力系数对α和δe的导数;CD0为零升阻力系数;CDα和CDα2分别为阻力系数对α和α2的导数;Cm0为零迎角俯仰力矩系数;Cmα为俯仰力矩系数对α的导数;Cmδe为俯仰力矩系数对δe的导数;Cmq为俯仰力矩系数对q的导数;cA为平均气动弦长。
考虑外界干扰,将式(1)写成如下形式:

2 RBF网络逼近
RBF网络为一种单隐层神经网络,学习收敛速度快。分别使用单输出RBF网络在线逼近

3 抗饱和非线性飞行控制系统
在起飞爬升过程中,通过控制航迹倾斜角来控制飞行器按照一定爬升率进行爬升,航迹倾斜角的控制过程如下所示。
其次,根据式(5)中迎角微分方程˙α=f30(x)+q+Δ3(t),由RBF网络在线逼近不确定项Δ3(x),采用反步方法设计俯仰角速度虚拟控制信号qd为

式中:Mδe为限幅最大幅值;τδe为时间常数。
在升降舵出现饱和时,上述反步控制信号已无法保证闭环控制系统的稳定性。这里根据所需升降舵偏角和实际升降舵偏角设计抗舵偏饱和动态补偿系统,对前级俯仰角速度虚拟控制信号进行修正,以期解决该问题。
设计抗舵偏饱和动态补偿系统为
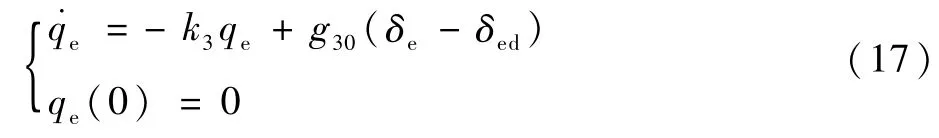

利用补偿信号qe对俯仰角速度虚拟控制信号进行修正:
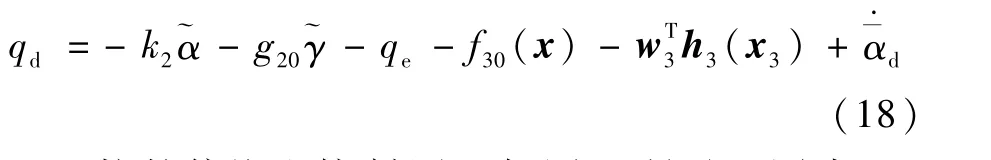
抗舵偏饱和控制原理如图1所示。图中:kfq为一阶滤波器参数[15]。当舵面出现饱和现象时,通过上述抗饱和动态补偿系统即可得到补偿信号qe,对俯仰角速度虚拟控制信号进行动态修正,帮助系统快速脱离饱和,恢复到正常控制。

图1 抗舵偏饱和控制原理Fig.1 Schematic diagram of control against rudder deflection saturation


抗发动机转速饱和控制原理如图2所示。当发动机转速出现饱和时,抗饱和动态补偿系统输出的信号Ve被反馈到速度控制系统的前馈通道中。通过设计合适的控制参数kp和kI,可帮助系统在较短时间内脱离饱和,直至Ve恢复为零。

图2 抗发动机转速饱和控制原理Fig.2 Schematic diagram of control against engine speed saturation
4 闭环控制系统稳定性分析
本节对航迹倾斜角控制系统和飞行速度控制系统的稳定性进行分析。
分别定义李雅普诺夫函数V1和V2:

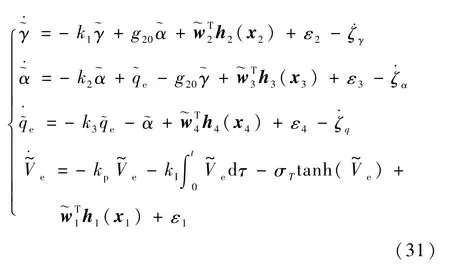
根据αd和qd的表达式,且γd为二阶指令滤波器[16]获得的足够光滑的指令信号,并利用假设1可得如下不等式:

对式(28)进行求导,将式(31)和式(32)代入其中,整理化简后可得

式中:σ4>0为设计参数。


综上所述,以上所设计的升降舵偏角控制信号、发动机转速控制信号和RBF网络自适应律可确保航迹倾斜角和飞行速度跟踪误差稳定收敛。
5 仿真分析
被控对象:飞行器质量28 kg、平均气动弦长0.5 m、翼展3.5 m、机翼参考面积1.7 m2,升力系数对迎角的导数为4.7,阻力系数对迎角的导数为0.11,俯仰力矩系数对迎角的导数为-2.2,俯仰力矩系数对俯仰角速度的导数为-20.5。通过如下仿真对所设计的抗饱和飞行控制系统的有效性进行验证。
1)仿真1。飞行器初始水平飞行,初始飞行速度为30 m/s,爬升角指令为20°,飞行速度保持,升降舵偏角限制在±15°,加入15%的建模误差。图3给出了加舵偏饱和补偿系统和不加补偿系统的对比曲线。可以看出,加入补偿系统后,在舵偏出现饱和时,抗饱和动态补偿系统输出补偿信号,如图3(d)所示,其可对前级指令信号进行修正,帮助系统快速恢复到正常控制,避免过长时间的舵控饱和,整个过程能够对给定指令进行稳定跟踪。
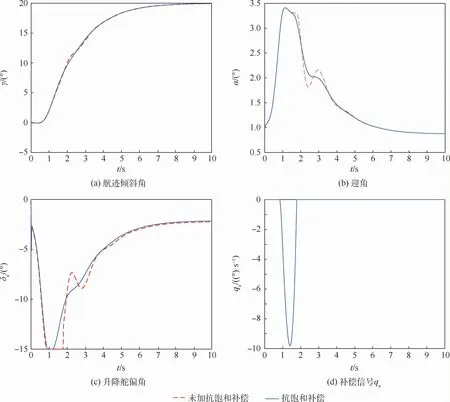
图3 仿真1曲线Fig.3 Curves of simulation 1
2)仿真2。飞行器初始水平飞行,初始飞行速度为25 m/s,在仿真初始时刻让飞行速度增加到50 m/s,发动机转速限制在99 r/s。图4给出了加发动机转速饱和补偿系统和不加补偿系统的对比曲线。可以看到,在加速的过程中,发动机的转速达到饱和。在没有加补偿系统时,发动机转速饱和时间较长,在发动机转速饱和时间内飞行速度跟踪误差较大。由于在加入补偿系统后补偿信号在发动机转速饱和时间内值不等于零,对发动机转速饱和起到一定的抑制作用,使得系统在较短的时间内脱离饱和,缩短了发动机转速饱和时间,飞行速度能够较快地跟踪指令信号。通过上述仿真结果可知所设计的抗饱和补偿系统基本满足设计要求,飞行控制系统可行有效,具有较高的鲁棒性。
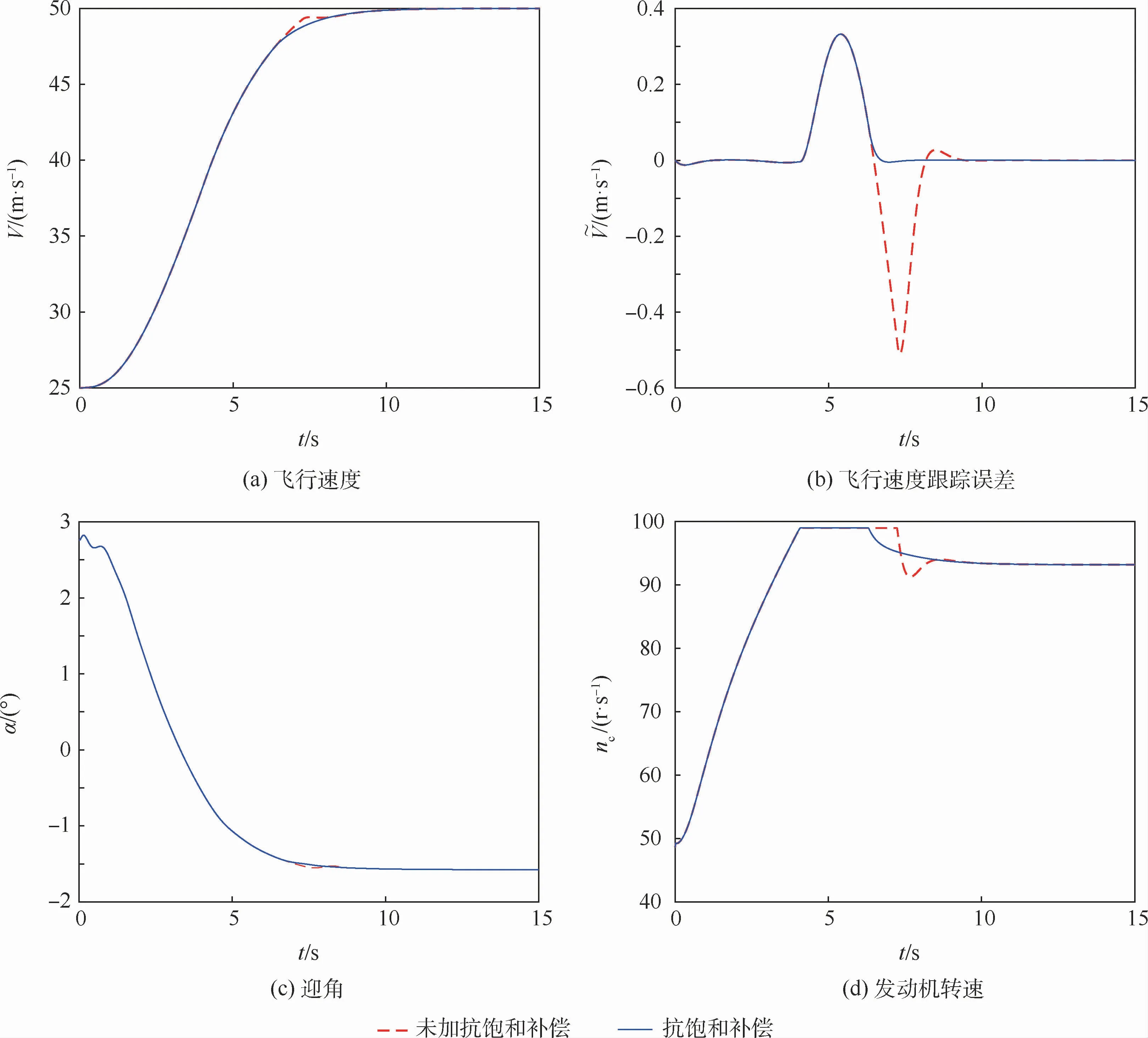
图4 仿真2曲线Fig.4 Curves of simulation 2
6 结 论
针对飞行器在机动飞行过程中控制机构易出现饱和的问题,本文设计了一种抗饱和非线性鲁棒控制方法。通过仿真结果可以看出:
1)在舵偏和发动机转速达到饱和时,对指令的跟踪精度较差,跟踪误差要大于未饱和时的跟踪误差。
2)在控制系统出现饱和时,相应的抗饱和动态补偿系统输出补偿信号,补偿信号对舵偏和发动机转速饱和起到一定的抑制作用,直至系统恢复到正常控制。
3)动态抗饱和补偿系统可使控制系统在较短时间内消除饱和。加入抗饱和补偿系统后,控制系统的饱和时间缩短了约30% ~60%。
本文方法具有一定实用性和普适性,可推广应用于其他抗饱和控制系统设计中。

