石墨烯改性沥青界面力学性能的分子动力学模拟*

周 昆，黄 君，邓雅丹，黄立新，2

(1.广西大学 土木建筑工程学院，南宁 530004；2.广西大学 工程防灾与结构安全教育部重点实验室，南宁 530004)

0 引 言

沥青作为工程领域常用的材料之一，广泛应用于道路铺装、桥面铺装等。因其工作环境长期处于室外暴露环境下，极易受到温度、日照、水损等多方面的影响。因此常添加其他材料对沥青进行改性，以改善沥青的路用性能。改性沥青是向沥青基体加入改性剂或其他外掺剂的方法，常用的沥青改性剂包括橡胶、树脂、碳纳米材料、各类聚合物等。改性剂的加入可以提高沥青弹性、软化点等多种特性。石墨烯作为近几年来热门的碳纳米材料，其优异的力学、热学、电学性能获得了研究者的广泛关注[1]。但是由于石墨烯为二维材料，并且其弯曲刚度极小，这使得它极易产生褶皱和缺陷等问题。因此单独将其作为结构材料具有较大困难。而石墨烯比表面积大的特点使得其能与其他材料充分结合，故近年来学者们开始研究石墨烯在复合材料中的运用[2]。研究发现，石墨烯对沥青的改性能够有效提高沥青在高温、低温、抗老化方面的表现[3]，并且能够提高沥青路面的耐变形性能、减少车辆动荷载下的车辙效应[4]。但石墨烯作为单纯沥青改性剂，在微观层面的稳定取决于石墨烯与沥青之间的界面关系。界面的缺陷会严重影响沥青的力学性能和破坏强度[5]，因此在改性沥青的众多性能中，界面力学性能的研究显得尤为关键。

在沥青复合材料界面性能实验研究方面已经取得了许多成果。文献[6-7]利用光学与电子显微镜对多孔沥青混凝土微观界面形状进行了直接观察。Liu[8]使用扫描电镜、红外光谱等方法研究了沥青与钢渣骨料的黏附、界面微观结构等界面相关性能，从物理吸附和化学反应两方面分析了沥青与钢渣骨料的黏附机理。Yin[9]使用动态剪切流变仪测试了沥青与花岗岩的剪切流变性能，并利用X射线光电子能谱分析了二者之间的黏附性能。此外，文献[10-11]采用通用试验机和气动黏附拉力试验机进行改性沥青的拉拔实验，研究沥青与集料在水分存在下的界面张力破坏。

虽然实验能给出宏观状态下沥青与沥青混合料的相关粘结强度，但实验费时费力，并且所测量到的界面行为受到了增强材料性质的影响，如孔隙率、水分、纯度等。并且沥青与骨料之间的界面黏附行为依赖于不同分子基团之间的分子相互作用[12]。因此近年来，文献[13-14]采用分子动力学模拟(molecular dynamic，简称MD)计算结构的性质。

因此，本文采用MD模拟方法研究石墨烯改性沥青的分离行为，旨在探讨不同因素对石墨烯改性沥青的界面力学性质影响。首先通过MD得到沥青的物理性质，并与其他实验进行对比确认模型的正确性。之后通过对模型施加速度来达到拉拔实验的目的，进而得到界面应力分离曲线。并与宏观实验下得到的内聚区模型进行比较。最后分析了加载速率对石墨烯改性沥青界面破坏的影响。

1 分子动力学模拟方法

1.1 模 型

沥青是一种高度复杂的材料，包含105～106种不同的分子[15]。因此选取能够体现沥青物理化学性质的分子模型是MD模拟的基础。Li[16]选择了美国战略公路研究计划(strategic highway research program)的3种沥青体系：AAA-1、AAK-1、AAM-1。它们分别代表来自Canadian/Lloydminster(AAA-1), Venezuelan/Boscan(AAK-1)和 USA/West Texas(AAM-1)的原油来源。在对这3种沥青系统进行元素分析、分子类别选取、以及各组分质量分数适配后，确定了沥青的4组分模型。4个组分分别为：沥青质(asphaltene)、饱和烃(saturates)、环烷芳烃(Naphthene aromatics)、极性芳烃(Polar aromatics)。这4个组分总共包含12个分子，单个分子结构如图1所示。因为该模型在研究沥青结合料内聚性能和粘合性能上具有明显优势[17]，所以本文选用该模型进行石墨烯/沥青界面力学性能的研究。沥青模型各个分子的信息列于表1。

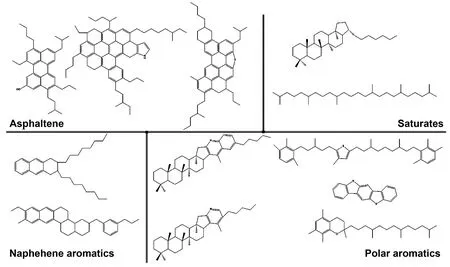
图1 沥青四组分模型

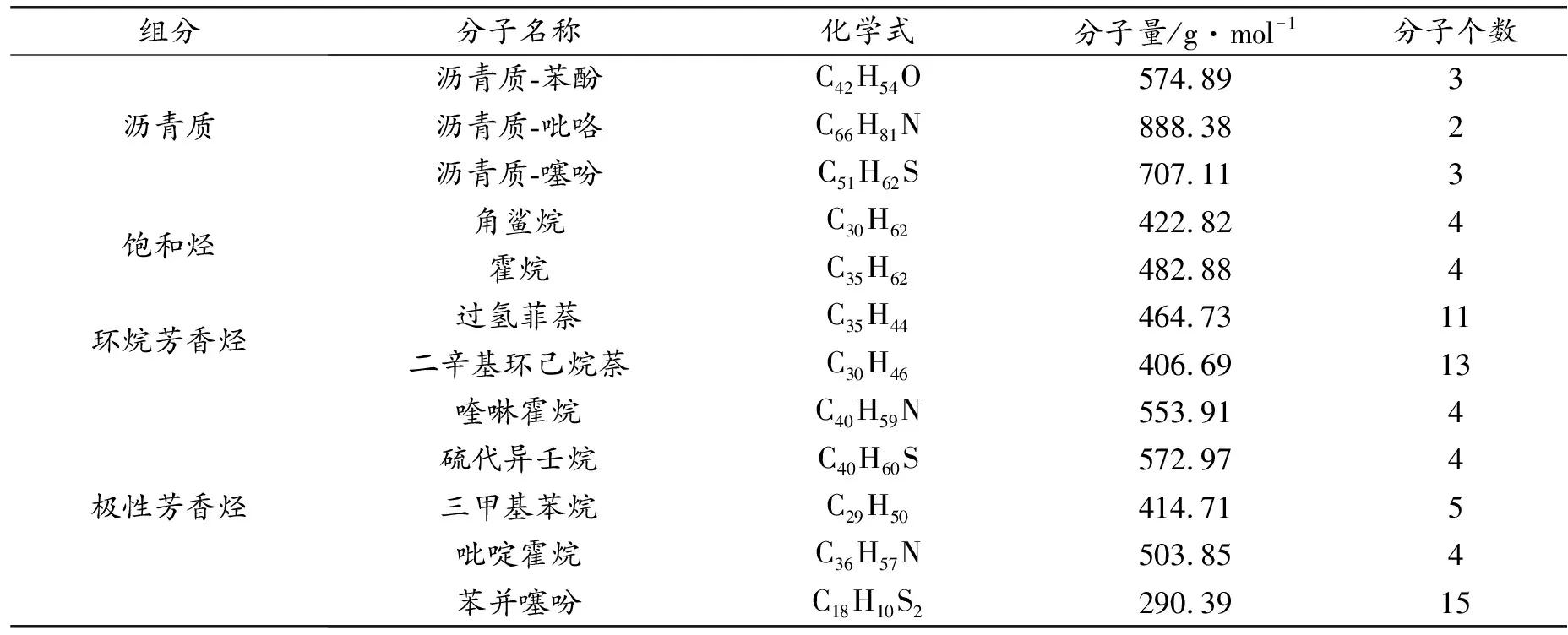
表1 沥青四组分模型参数

石墨烯单胞尺寸为a=0.246 nm，b=0.426 nm，c=3 nm，α=β=γ=90°，如图2(a)所示。为建立石墨烯/沥青复合材料界面模型，石墨烯片尺寸须同沥青尺寸相近。因此，导入石墨烯单胞模型后，以A=16，B=10，C=1的超晶胞范围(supercell range)建立超晶胞。并以(0 0 1)为切割面法向量进行切割，从而得到所需要的单片石墨烯表面，如图2(b)所示。二维石墨烯片尺寸为u=3.935 nm，v=4.256 nm，θ=90°。然后添加1.0 nm真空层将石墨烯片从二维变为三维。最后联合石墨烯与沥青建立界面模型。

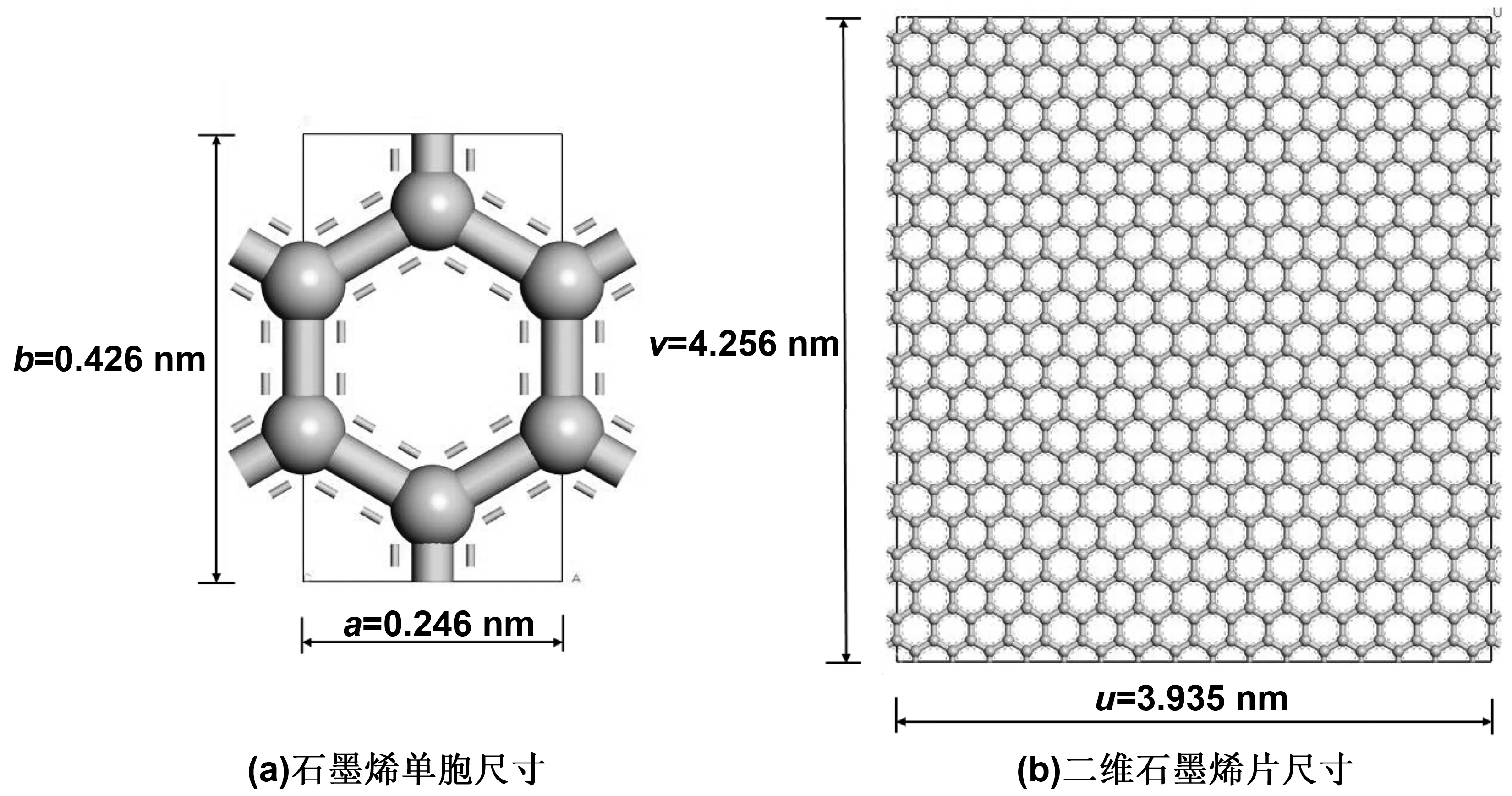
图2 模拟采用的石墨烯片参数

1.2 力场

石墨烯与沥青之间的作用力通过力场来定义。本研究采用OPLS-AA力场(Optimized Potentials for Liquid Simulations all-atom)。该力场对有机液体、生物大分子等物质有更为精确的拟合效果[18-20]。OPLS-AA力场包含了价态项和非键作用。价态项主要包括键伸缩、角弯曲、二面角扭转。非键作用由静电相互作用和van der Waals相互作用组成。OPLS-AA力场各种相互作用的势函数形式为：

Etotal=Ebonds+Eangles+Edihedral+Enon-bonds

(1)

(2)

(3)

(4)

(5)

式中，Kr、Kθ、Vn和φ分别表示与键长、键角、二面角有关的经验参数。共价键伸缩势Ebonds和键角弯曲势Eangles采用谐振子势函数，二面角扭曲势Edihedral取Fourier展开式前4项。van der Waals相互作用采用Lennard-Jones 12-6势函数，采用Lorentz-Berthelot混合规则计算交叉项参数。静电相互作用采用库伦势函数，当i，j为1，4时，fij=0.5(表示分子间和分子内1，4相互作用)，否则取1.0。本文中van der Waals相互作用与静电相互作用的截断半径均取1.0 nm，超出10 Å的库仑力使用PPPM(particle-particle particle-mesh)方法进行计算。

1.3 模拟设置

宏观状态下，石墨烯改性沥青处于非均匀状态，石墨烯随机分布在沥青基体当中，如图3(a)所示。石墨烯/沥青复合材料界面的复杂性主要是由于沥青无定形性质的结果，并且没有特定的模型来描述微观状态下沥青与石墨烯平衡时的界面状态。对这样的体系进行分析时，不可能将所有夹杂结构进行分析。为降低模拟复杂程度，因此须取一个如图3(b)所示的代表体积单元(representative volume element,简称RVE)。该微元界面处的分离行为可以看作复合材料下有效的界面本构关系，实际上是以均匀的微元来替代宏观状态下非均匀状态。在本项工作中，因仅研究石墨烯改性沥青界面分离响应，无关其他物理化学性质，因此实验假定石墨烯是平坦无缺陷的。并且石墨烯与沥青基体之间不存在化学键，最终所取RVE如图4所示。

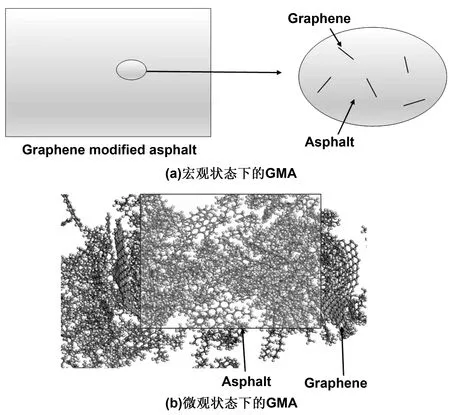
图3 代表体积单元的选取

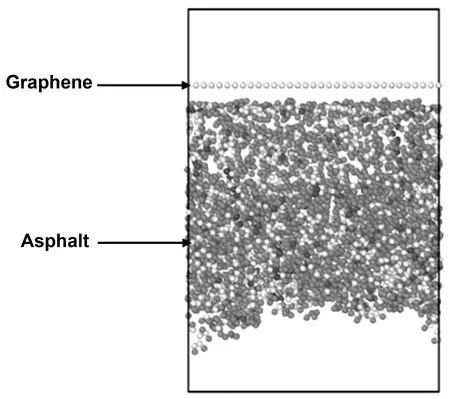
图4 石墨烯改性沥青代表体积单元

复合材料界面粘结强度主要由拉拔实验确定，通过石墨烯与沥青分离的过程可以确定材料破坏机制。因此，在基于RVE的基础上，使用MD模拟方法模拟拉拔实验，以研究原子尺度上石墨烯与沥青分离的机制。确定RVE以后，为了考虑除RVE外的其他地方的影响，模拟时在xyz3个方向均为周期性条件。运用周期性边界条件的缺点是没有足够距离实现界面脱离，因此需要在拉伸方向添加足够的真空层，本文中在拉伸方向添加了2.0 nm真空层。

建立好模型后，使用CG(conjugate gradient)方法进行能量最小化处理。然后对模型进行足够的弛豫，弛豫时间取500 ps。为了得到模拟温度下的构型，在NVT系综下使用Nose-Hoover恒温器进行500 ps的弛豫。拉拔模拟时忽略石墨烯变形，因此将其设置为刚体。为避免石墨烯同沥青一同运动，需要将底部一定范围内的沥青进行固定。给石墨烯设置一个恒定速度向上移动，从而实现分离界面分离。整个分离过程记录石墨烯所受到的牵引力。通过将该牵引力除以石墨烯面积得到所需要的拉拔应力。

MD模拟中，过小的时间步长会导致计算资源的浪费，过大则会导致积分计算不稳定。文献[21]指出，最合适的时间步长是通过NVE的能量波动来选定的。因此在拉拔模拟过程中，以1 fs的时间步长对运动方程进行积分，并选择使用阻尼系数为10 fs的langevin恒温器控制体系温度。阻尼系数以时间为单位，决定着体系松弛速度。本研究选取10 fs作为阻尼系数，这代表着体系温度每10 fs松弛一次，这样能很好地控制温度。

沥青与石墨烯建模均在Material Studio中进行，并结合LigParGen[22]在线网站确定沥青在OPLS-AA力场下的参数。另外，石墨烯力场参数取自文献[23]。之后采用自行开发的MATLAB程序进行文件改写，并输入至LAMMPS(large-scale atomic/molecular massively parallel simulator)进行运算。模型与整个界面脱离过程使用可视化软件OVITO进行观察。

2 沥青的物理性质

界面拉拔测试的首要前提是确定模型的正确性，因此首先确定模型密度是否与真实沥青接近。首先以0.1 g/cm3的初始密度构建沥青无定形模型。之后使用NPT系综(p=1 atm，T=298 K)对该模型进行弛豫。弛豫过程中，随着模拟时间的增长，沥青晶胞体积缩小，分子间间隙逐渐减小，密度也因此上升。密度变化如图5所示。SHRP给出的AAA-1沥青的密度在常温常压下为1.03～1.04 g/cm3。本研究所得密度为1.006 g/cm3。沥青模型与真实模型密度上的差距，是由于MD模拟中仅考虑了12种分子类型，与真实沥青相比少了许多其他组分。密度仅相差0.024～0.034 g/cm3，属于合理范围内。

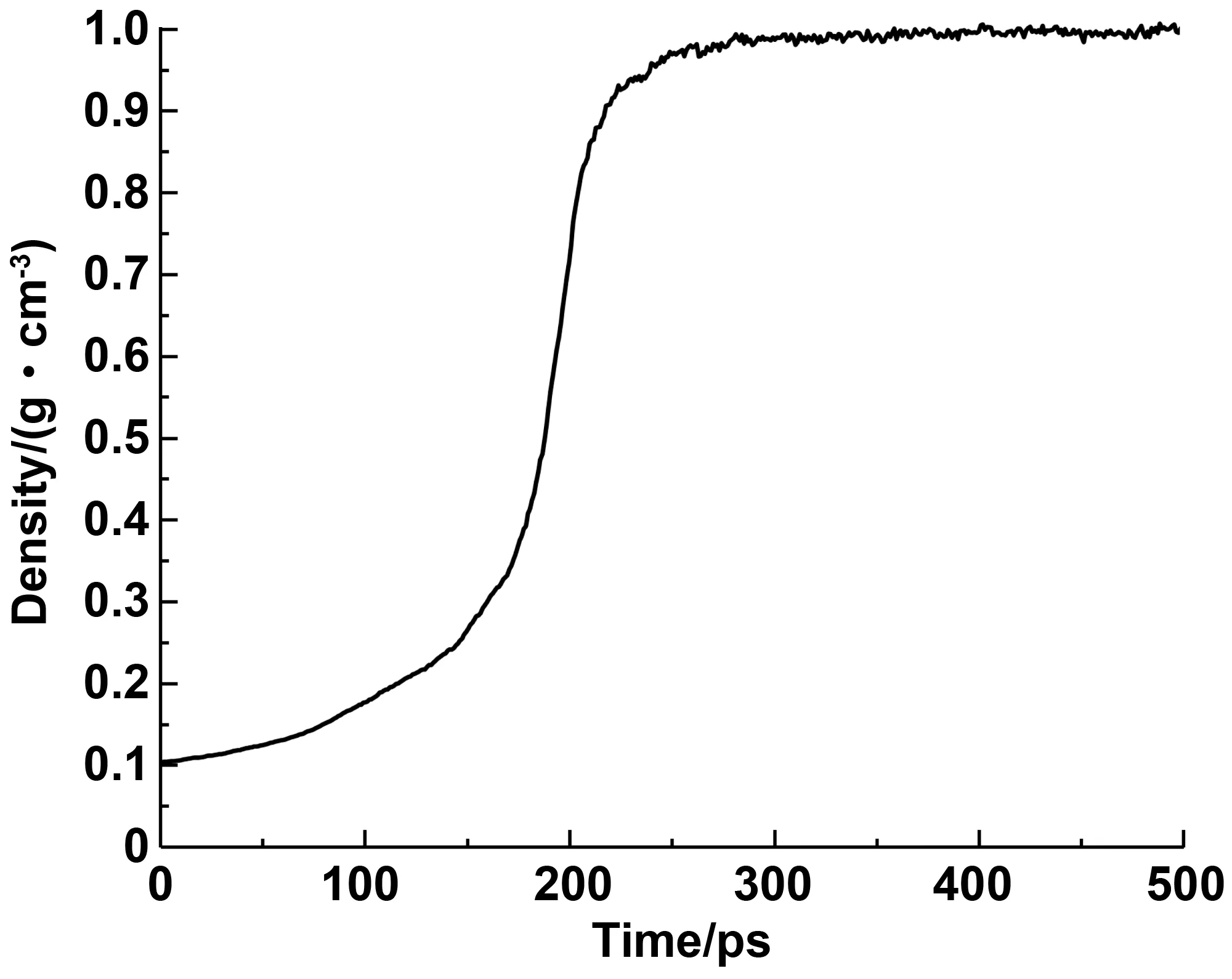
图5 NPT系综(T=298 K，p=1atm)下沥青密度

采用比体积曲线方法确定沥青玻璃化转换温度Tg。首先对体系进行能量最小化处理，而后使用NPT系综分别得到不同温度下的稳定构型。取208～478 K的温度区间，以10 K为间隔记录了10个温度下的沥青比体积，并根据不同温度下绘制比体积散点图，如图6所示。利用最小二乘法确定两条斜率不同的回归方程，两条回归方程交点即为所求Tg。计算得到的Tg为299 K，该温度将温度-比体积曲线划分为两个区间，左侧区域内比体积变化较缓，右侧区域内则变大。本文计算得到的Tg与文献的结果比较情况列于表2。从表中可以发现文献[24]使用弯曲梁流变仪测得的Tg为223～303 K，说明Tg属于一个温度范围，而不仅仅是一个特定的点，这主要取决于原油来源和测量方法。只要所测得的结果在该范围内，都是正确的。综合模拟所得密度与Tg，并与实验值对比后，验证了沥青模型的正确性以及OPLS-AA力场的适用性。

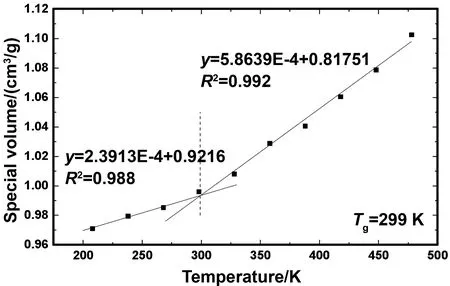
图6 GMA玻璃化转换温度的确定

表2 沥青玻璃化转换温度的文献对比

3 拉拔过程中的界面行为

3.1 界面分离过程

拉拔模拟的结果如图7所示，横坐标定义为石墨烯片向上移动的距离，纵坐标定义为石墨烯的分离应力。采用移动平均滤波法进行应力数据的收集，每100步(即100 fs)统计一次应力数据，每5个数据进行一次数据平均。该例子记录了温度为298 K时的分离情况，石墨烯片移动速率为10 m/s。记录了20万步的分离情况，这意味着石墨烯一共移动2.0 nm的距离。拉拔2.0 nm后，石墨烯与沥青已完全分离破坏。a点为初始状态，此时石墨烯片应力大于0，这是石墨烯与沥青之间相互粘结产生的吸引力控制的。而后随着基底向上移动，应力显著增加。曲线到b点(x=0.09 nm)后，达到峰值应力，随后在[0.09 nm，0.2 nm]区间内开始振荡。可以观察到此时沥青还未发生破坏，沥青间的作用力仍保持着沥青的完整性。随着位移增大，沥青与石墨烯片之间相互作用力减弱(c点)，界面应力迅速减小，开始振荡并最终减小为0(d点)。

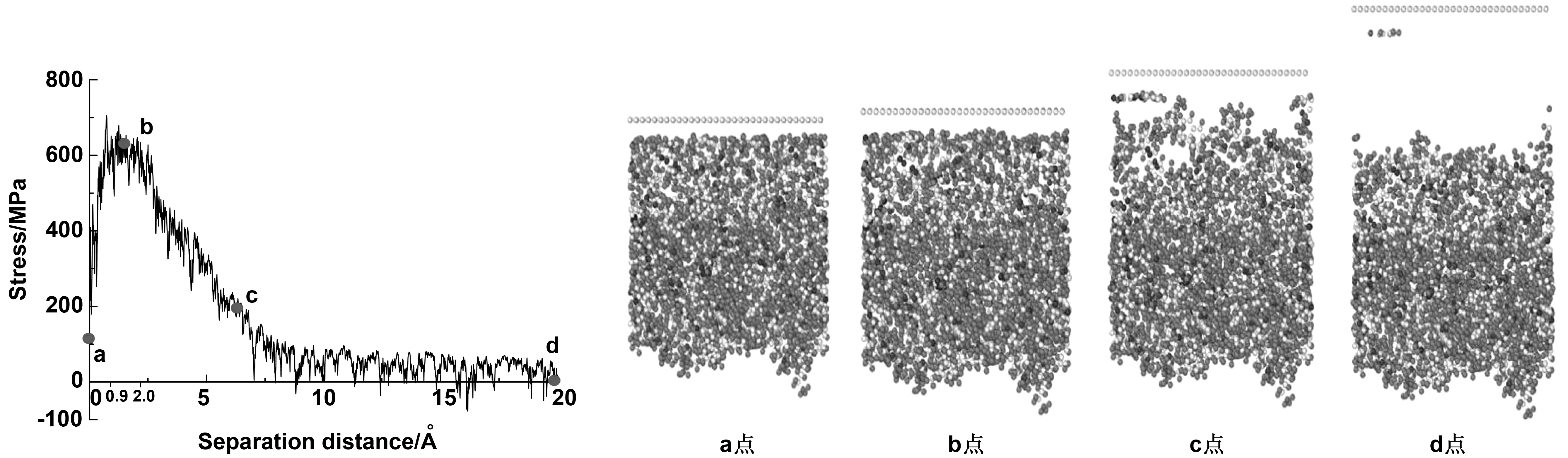
图7 石墨烯改性沥青的界面分离响应

当温度为常温，加载速率为10 m/s时，可以发现当石墨烯开始脱离沥青基体时，沥青首先是被拉伸，之后内部出现微小空隙，但这些空隙并未引起沥青基体内部结构失效。随着石墨烯片远离沥青，而不对其产生作用力时，此时定义为复合材料的破坏。因此10 m/s加载下，沥青与石墨烯界面破坏的机制是界面粘结破坏，而非内聚破坏。

3.2 内聚规律

模拟得到的应力-位移曲线与准脆性材料的内聚区模型(cohesive zone model，简称CZM)所给出的粘结规律相似。CZM是对沥青破坏机制参数化的一种模型，对于描述沥青的破坏机制给出了详细解释[29-30]。理想的CZM将材料断裂限制在两个零厚度的界面之间，其余区域内是没有破坏的。作用在裂纹上的牵引力随界面的分离距离而产生非线性变化，这与本研究所得结果一致。因此可以将MD所得规律同跨尺度模型结合在一起进行考虑。

CZM可以采用线性、双线性、梯形、光滑梯形、指数等不同的方法来描述[30]。本研究选取指数模型进行非线性拟合，因为这一模型与实验数据贴合较好，且能更好地反映峰值点过后软化过程。以应力最大值点σc，以及发生最大应力时的分离距离xc作为参数进行设置。函数模型如下：

图8给出了常温常压下(p=1 atm,T=298 K)使用MD模拟所得出的结果，以及使用指数内聚区模型拟合所得的曲线。拟合后得到应力在分离距离为0.1662 nm时达到最大值，即647.95 MPa。可以发现，指数内聚区模型与MD模拟所得数据吻合较好，内聚规律认为界面破坏发生在界面应力达粘结强度时。在达到峰值后，沥青进入软化状态。随着损伤的累积，界面应力逐渐降低，并减小至0。

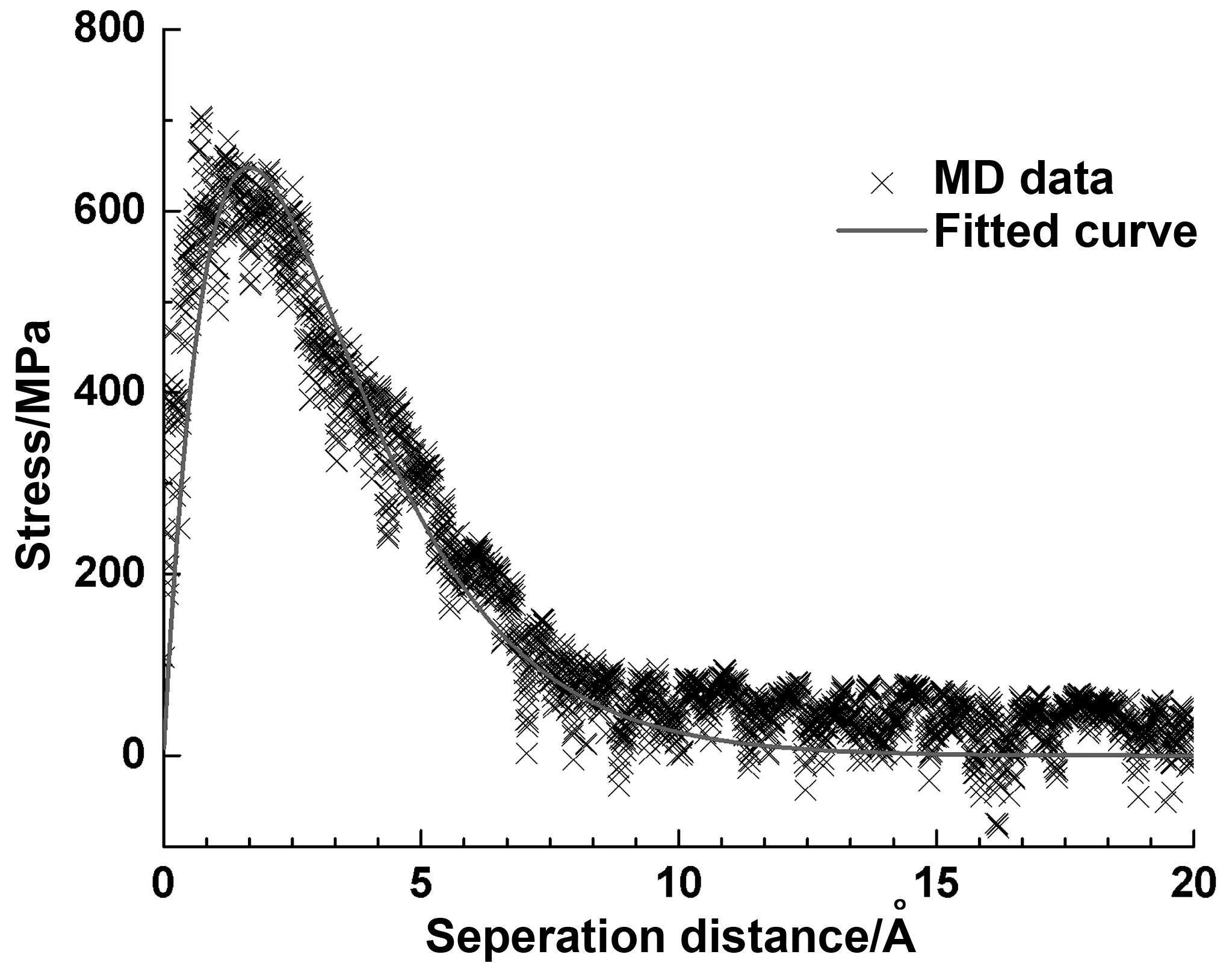
图8 拟合MD数据得到的内聚区模型

特别地，内聚规律其实是一种不可逆的规律。这一不可逆规律表现在加载-卸载-再加载这一过程中，再加载后所达到的界面应力值无法达到初次加载时的界面应力。这一过程用MD模拟所得结果如图9所示。图9(a)给出了在未达到界面峰值应力之前进行卸载的过程，可以看到再加载时峰值应力与初加载时的应力相近。图9(b)展示在达到界面峰值应力之后进行卸载的过程，可以发现再加载后无法达到原有的峰值应力。这意味着在界面应力达到粘结强度后发生了损伤，沥青内部结构的损伤导致其无法再保持原有强度。当然，这里需要指出，MD模拟因时间尺度和模型尺度上的限制，加载速率高于实验所能达到的速率，所以得到的界面应力远远超出实验值[31]。因此MD模拟仅能从微观角度解释沥青界面破坏机制，之后如要进行跨尺度研究，需要将微观机制与实验测量结合起来才能深入了解沥青的软化过程。

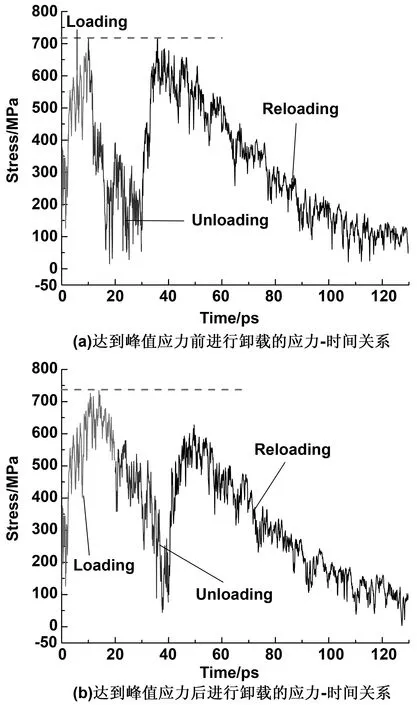
图9 内聚规律

3.3 不同加载速率下的界面行为

对于宏观状态下的沥青路面，工作过程中所受力的大小不一样，因此本小节讨论不同加载速率对破坏机制的影响。考察10、20、30 m/s等3种加载速率的影响，即每一步(t=1 fs)石墨烯片分别移动1×10-5、2×10-5、3×10-5nm的情况下，石墨烯改性沥青的破坏过程。图10给出了不同加载速率下的应力-位移曲线图。结果表明，低速率下(10 m/s)，即使在对数据进行移动平均处理后，曲线振荡仍然较为明显。主要是因为低速率拉拔时，仍然有部分沥青粘结在石墨烯上。并且应力达到峰值后，有较长一段的分离过程，属于延性破坏。而在高速率(20和30 m/s)下，曲线基本没有波动，到达一定位置界面应力就下降为0，这意味着界面的彻底破坏，属于界面粘结破坏。其次，30 m/s的破坏位置相较于20 m/s的破坏位置更为提前，并且到达峰值点的速度更快，应力峰值更大。这一趋势与宏观尺度下的实验得到的内聚规律一致[32]。以上3种速率加载时，均为界面粘结破坏，即破坏时是石墨烯与沥青的分离。

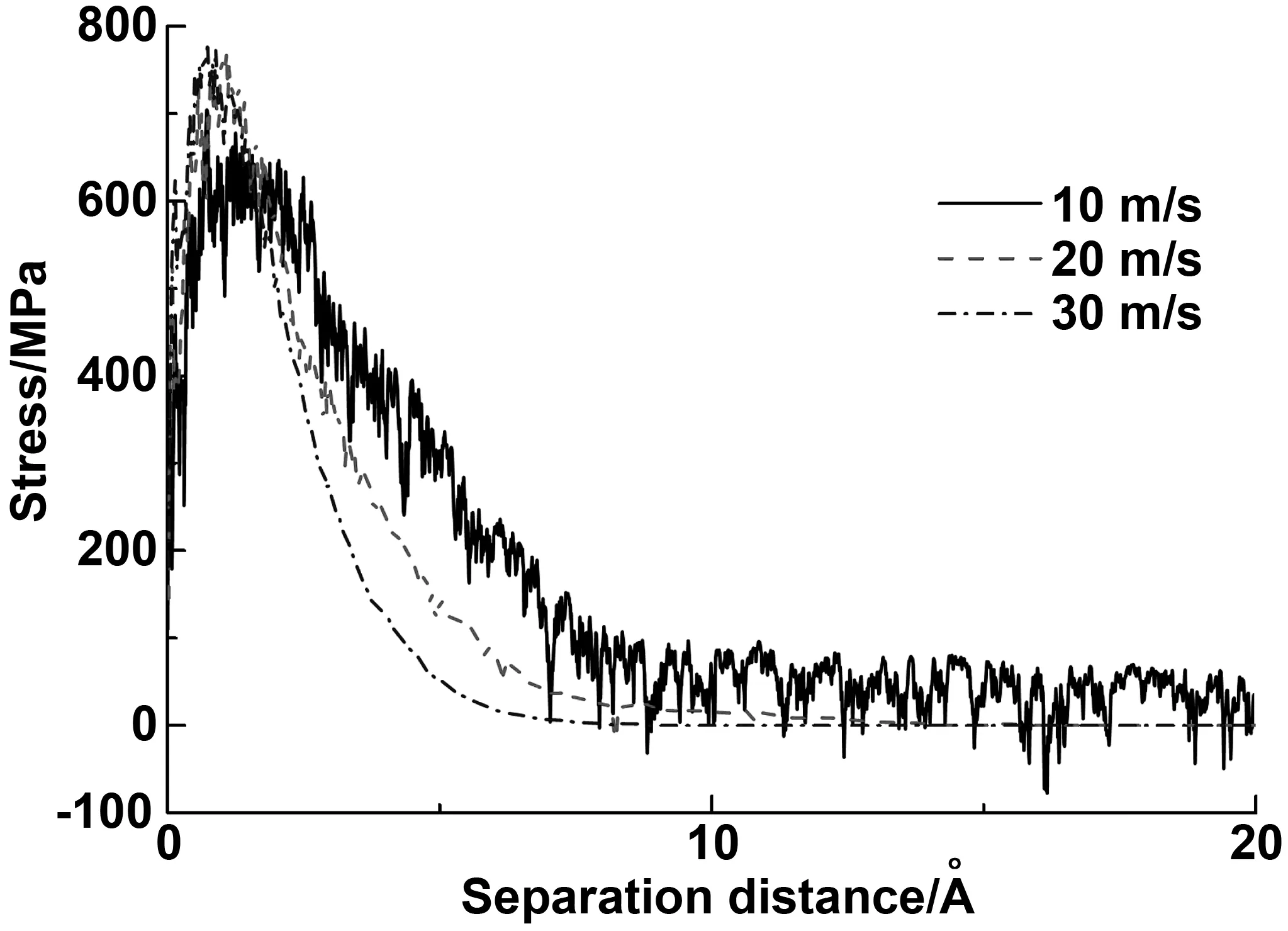
图10 不同加载速率下的拉拔过程

进一步考虑更低加载速率时石墨烯改性沥青的破坏情况，取5 m/s的加载速率。图11展示了石墨烯改性沥青的破坏过程，从图中可以看到低速率下所测得的最大拉伸应力会降低，且应力-位移曲线振荡幅度更加显著。这是由于石墨烯位移的增加使得沥青内部空隙逐渐增多，其余未破坏部分的沥青热运动就更加显著，从而大部分沥青产生较大的蠕变变形，并且黏附在石墨烯片上的沥青比高速率下黏附的要更多。不同于高速率下的界面粘结破坏，低速率下的拉拔破坏则为更严重的内聚破坏。

图11 低加载速率下(5 m/s)的应力分离响应

4 结 论

采用分子动力学模拟方法对石墨烯改性沥青的界面力学性能进行了研究。首先通过模拟得到常温常压(p=1 atm,T=298 K)下AAA-1沥青密度为1.006 g/cm3，与实验值相差不大。并通过计算不同温度下的比体积，使用最小二乘法进行线性拟合得到沥青玻璃化转换温度Tg=299 K。与实验值对比，Tg=299 K在正确的范围之内，验证了沥青模型的正确性。在此基础上，开展了石墨烯改性沥青分子动力学模拟的拉拔实验，得到如下结论：

(1)通过MD模拟得到10 m/s速率下的应力-位移关系，发现沥青与石墨烯的破坏属于界面粘结破坏，并且这一关系同宏观实验下得到的内聚规律趋势一致，应力先随位移增大而迅速上升，当达到峰值应力后则开始缓慢下降。而这一缓慢下降过程(软化过程)与指数型内聚区模型吻合最好。

(2)在达到界面粘结强度之前进行卸载时，石墨烯改性沥青保持弹性状态，此时的变形可逆。但在达到界面粘结强度之后卸载时，因沥青内部出现损伤，导致沥青变形不可逆，无法达到之前的粘结强度。

(3)通过对不同速率的拉拔实验得知，高加载速率下石墨烯改性沥青的界面破坏属于界面粘结破坏。而当加载速率下降到一定程度时，沥青在拉拔过程中出现大块空隙，形成孔洞，属于内聚破坏。

从上述方面可以确定，MD模拟所得结果与实验值偏差属于容许范围内，并且可以与更大高尺度模型相结合，为全面分析石墨烯改性沥青的界面力学性能提供更加全面的解释。