基于XGBoost和改进灰狼优化算法的催化裂化汽油精制装置的辛烷值损失模型分析
陈延展,胡 浩,任紫畅,成艾国
(湖南大学 机械与运载工程学院,湖南 长沙 410000)
汽油是小型车辆的主要燃料,其燃烧产生的尾气排放对大气环境有重要影响。为此,世界各国都制定了日益严格的汽油质量标准。研究法辛烷值(RON)是反映汽油燃烧性能的最重要指标,并作为汽油的商品牌号(例如89#、92#、95#)。现有技术在对催化裂化汽油进行脱硫和降烯烃过程中,普遍降低了汽油辛烷值[1]。辛烷值每降低1个单位,相当于损失约150 CNY/t[2]。以一个1000 kt/a催化裂化汽油精制装置为例,若能降低RON损失0.3个单位,其经济效益将达到45×106CNY。因此,研究汽油的辛烷值,对于保护大气环境和提高工厂经济效益具有重要意义。
实验测定是目前获取汽油辛烷值数据的最有效方法。根据ASTM D2699[3]和ASTM D2700[4]的规定,辛烷值分为研究法辛烷值(RON)和马达法辛烷值(MON)2种。通过实验测定来改善调试汽油样品的辛烷值从而确定其最佳配比,不仅需要昂贵的实验仪器及设备,还需要花费大量的时间及试剂样品[5]。因此,有必要开展汽油辛烷值的理论预测研究,建立可靠的理论预测模型,弥补实验方法的缺陷与不足。
目前,分析化学法是文献中预测汽油辛烷值的常见方法。Ghosh等[6]通过色谱分析法来预测汽油辛烷值,平均误差值约为4~7个单位。Kardamakis等[7]则通过近红外光谱法对汽油辛烷值进行预测研究。分析化学法的缺陷在于同样需要用到相应分析测试仪器,其运转、维护费用较高,且耗时耗力。因此,采用各种理论算法来建立汽油辛烷值的预测模型受到广泛关注。
目前为止,基于各种理论方法的汽油辛烷值的化工过程建模一般是通过数据关联或机理建模的方法来实现的,取得了一定的成果。但是由于炼油工艺过程的复杂性以及设备的多样性,它们的操作变量(控制变量)之间具有高度非线性和相互强耦联的关系,而且传统的数据关联模型中变量相对较少、机理建模对原料的分析要求较高,对过程优化的响应不及时,所以效果并不理想。基于此,笔者利用某石化企业催化裂化汽油精制装置采集的大量历史数据,通过机器学习技术建立汽油研究法辛烷值(RON)损失预测模型,揭示相应的操作变量及其影响规律;并提出一种改进的差分灰狼优化算法对影响汽油辛烷值损失的操作变量进行优化,以尽量减少汽油精制过程中的辛烷值损失,为石化企业和运营商提供决策分析。
1 模型及算法介绍
XGBoost(Extreme gradient boosting)是由Zhou等[8]提出的一种支持并行计算的梯度提升树模型,近些年该模型凭借突出的效率和较高的预测精度被广泛应用于Kaggle机器学习竞赛中。实际上XGBoost是一种改进的GBDT(Gradient boosting decision tree)算法[9],两者本质上均由许多用于回归和分类的决策树组成,但是XGBoost在以下方面对GBDT算法进行了改进:(1)对于损失函数,GBDT算法只使用了一阶泰勒展开,而XGBoost则增加了二阶泰勒展开;(2)XGBoost在目标函数中构造了正则惩罚项[8]以降低模型复杂度,从而防止模型过拟合。XGBoost模型的结构如图1所示。

图1 XGBoost算法示意图Fig.1 Schematic of XGBoost algorithm
对于一个给定的有n个样本的数据集D={(xi,yi)}(i=1,2…,n),其中xi表示第i个样本的特征值集合,yi表示第i个样本的标签值,则基于数据集D训练出的具有K个基学习器的XGBoost预测模型为:
(1)
F={f(x)=ωq(x)}
(2)

(3)
在对训练数据进行学习时,每次在保留原有模型不变的基础上,加入一个新函数ft,观察对应的目标函数J(ft),若加入的新函数能使目标函数尽可能减到最小,则把该函数加到模型中。此时目标函数表示为:
(4)
(5)
式中:L代表损失函数;Ω(ft)则表示模型的复杂度;T表示叶节点数;γ和λ表示惩罚项的权重系数。之后对目标函数进行二阶泰勒展开得到如下近似目标函数:Tt为t次迭代后的叶节点数。

(6)
(7)
(8)
式中:gi和hi是关于损失函数L的一阶导数和二阶导数。综上所述,最终求得的目标函数形式如下:
(9)

(10)
(11)
2 特征工程
实验数据集来源于某石化企业催化裂化汽油精制装置运行4年所采集到的325个样本数据,其中每个数据样本都包含7个原料性质、2个待生吸附剂性质、2个再生吸附剂性质、2个产品性质等变量以及另外354个操作变量,共计367个特征变量。表1中仅列出367个变量中的前30个具体信息(由于变量太多,此次降为30个)。由于367个特征变量中存在大量的冗余变量,不利于汽油辛烷值损失值预测模型的建立和求解,所以利用特征工程筛选出建模的主要变量,特征工程的总体流程如图2所示。

表1 影响汽油辛烷值损失的特征变量Table 1 Characteristic variables affecting octane loss in gasoline

MIC—Maximum mutual information coefficient method图2 特征工程的主要变量选取流程图Fig.2 Flow chart for selection of key variables
由图2可知:首先需要对数据集进行归一化处理,由于各特征的数值量纲之间存在较大差异,数据归一化可以使所有特征具有零均值和同一阶数上的方差,以方便后续的机器学习模型训练;然后运用方差阈值法的思想进行特征的粗略筛选,计算数据特征的方差值,剔除方差较低的特征,得到剔除后的前100个变量特征;然后分别利用Pearson相关系数法、最大互信息系数(MIC)法和基于随机森林的特征选择法对各特征进行重要度计算;最终利用3种特征选择方法的融合进行变量特征的精确筛选。Pearson系数法仅反映不同变量之间的线性关系,最大互信息法能同时反映变量间的线性和非线性关系,基于随机森林的特征重要度排序方法以包裹式的特征选取方式进行特征重要度计算。考虑到选取的特征应具有独立性、代表性的要求,因此,按照Pearson系数法权重∶最大互信息系数法权重∶随机森林法权重比为2∶3∶5进行特征重要度的融合。各类方法对于特征变量的重要度排序如图3所示。

图3 各方法的特征重要度排序Fig.3 Feature importance ranking sequence of each method(a)Pearson method;(b)Maxmium mutual information coefficient method;(c)Random forest method;(d)Weight coefficient method
基于权重法融合结果的前25项特征的重要度之和占所有特征重要度之和的95%以上,故从得到的前100个特征中选取前25个特征作为建模的主要特征,其特征变量如表2所示。

表2 建模选取的主要特征变量Table 2 Main characteristic variables
3 模型应用与结果分析
以特征工程后的催化裂化汽油精制装置历史运行数据为训练集,分别采用多个机器学习模型建立汽油辛烷值损失值与25个主要特征变量之间的映射函数,并在测试集上利用各种评价指标进行模型对比,从而验证XGBoost模型的预测性能。
3.1 模型评价指标

(12)
(13)
(14)
3.2 实验分析与模型对比
基于催化裂化汽油精制装置历史运行数据分别训练了XGBoost汽油辛烷值损失值预测模型和其他机器学习模型,如线性回归模型[10]、K近邻模型[11]、支持向量机(SVM)[12]、决策树(DT)[13]和随机森林(RF)[14]等。实验平台为AMD Ryzen 74800H with Radeon Graphics(2.90 GHz),配置了16.0 GB的RAM内存和8 GB的GTX 1070Ti显卡。其中SVM、DT和RF等模型均在python的第三方库scikit-learn中实现。表3给出了上述10个机器学习模型对于汽油辛烷值(RON)损失值的预测精度、训练时间和测试时间。
由表3可见,后6个模型的R2均超过0.97而具有很高的预测精度,并且其中模型RF和XGBoost的R2均高达0.99以上,远超其他模型。表现最为突出的XGBoost模型R2值更是高达0.9981,并且MAE和RMSE均处在所有模型的最低值。然而2种线性模型LR和Linear-SVM的预测精度都很差,其R2均在0.95左右,证明了汽油RON损失值与25 个特征变量之间存在明显的非线性关系。其他模型DT和KNN的预测精度则处于中等水平。

表3 不同汽油辛烷值(RON)损失值预测模型的对比Table 3 Comparison of different RON loss value prediction models
XGBoost模型预测的汽油辛烷值损失值与真实值的对比曲线如图4所示。由图4可以看出XGBoost模型的拟合效果很好,两条曲线几乎完全重合。为了进一步说明XGBoost模型的拟合效果,图5绘制了测试集数据中汽油辛烷值损失的真实值与XGBoost模型预测值之间的散点分布,散点越接近直线则表示模型的预测能力越强[15]。从图5可以直观看出该模型具有良好的汽油辛烷值预测能力。
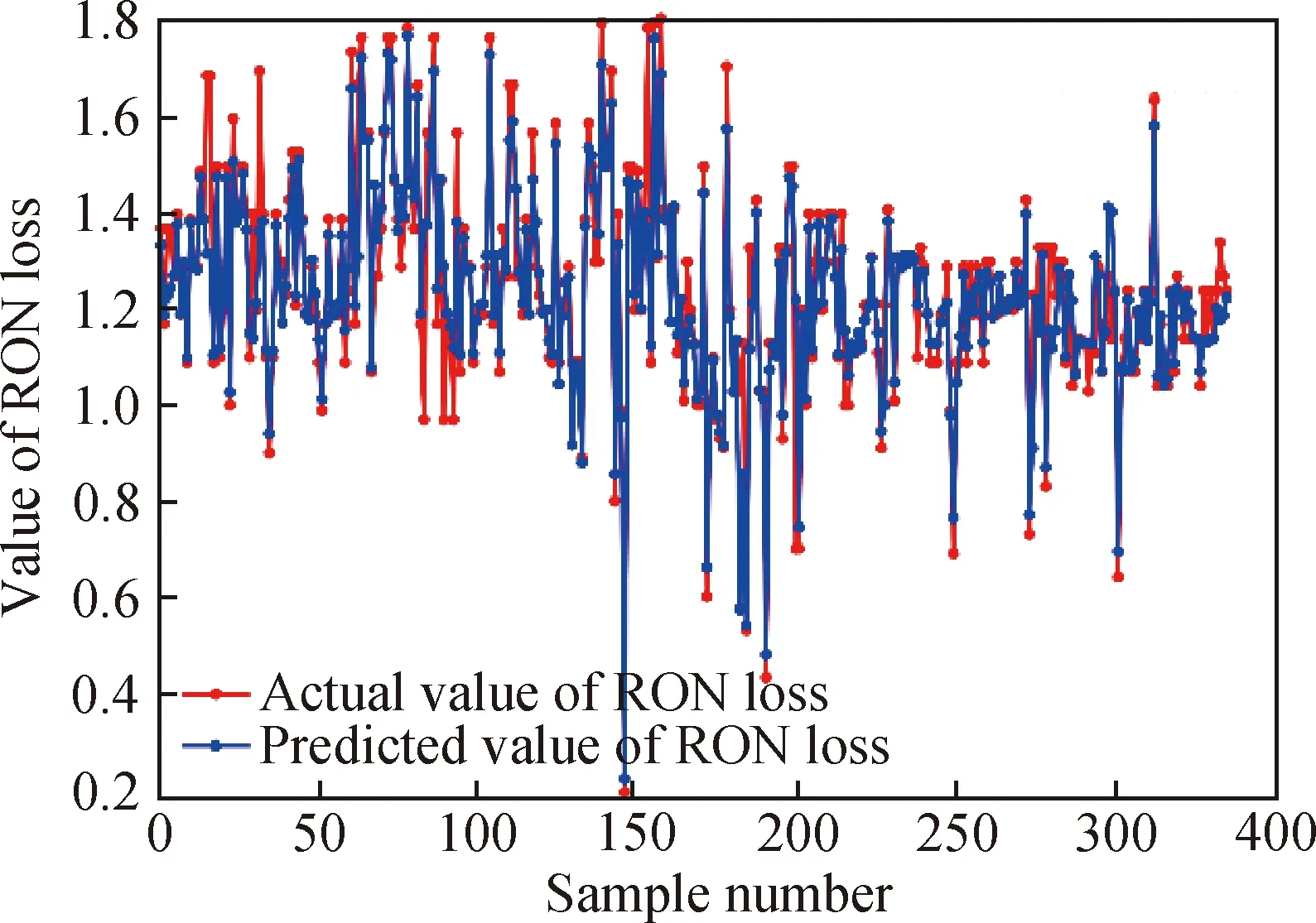
图4 XGBoost模型汽油辛烷值(RON)损失预测值与真实值对比Fig.4 Comparison of RON loss predicted values by XGBoost model and actual values

图5 XGBoost模型汽油辛烷值(RON)预测值与真实值的散点分布Fig.5 Distribution of RON loss predicted values by XGBoost model and actual values
综上所述,XGBoost模型的R2最高,并且训练时间、预测时间、MAE以及RMSE均相对较小。所以XGBoost模型在预测汽油辛烷值损失值的问题上比其他模型更加有效,笔者最终采用XGBoost模型预测汽油辛烷值的损失值。
4 基于改进差分灰狼算法的汽油辛烷值损失优化模型
为尽可能降低汽油辛烷值损失,同时由于国六车用汽油标准要求硫质量分数不大于5 μg/g,为了保证汽油产品脱硫效果,对数据样本的25个特征变量进行优化,建立了一种单目标优化模型。约束条件包括硫含量、操作变量的取值范围等。为了建立硫质量分数不大于5 μg/g的约束条件,同样采用XGBoost建立了硫含量与这些操作变量的映射函数关系,并作为限制条件求解。由于该优化模型的变量有25个,维度较高,笔者提出了一种改进的差分灰狼优化算法进行求解,可以较大提高模型的求解精度和效率。结果表明模型的建立与求解过程是合理的。具体的求解思路如图6所示。

图6 基于改进的差分灰狼优化算法的汽油辛烷值(RON)损失优化模型的建立与求解过程Fig.6 Establishment and solution of RON loss optimization model
4.1 模型建立
由数据可知,大多数样本的汽油辛烷值损失还是偏大的,有必要对其特征变量进行优化来减少其损失值。因此,建立了一个优化模型,并在保证硫质量分数不大于5 μg/g的条件下,分别对这325个样本对应的操作条件进行优化求解。具体的建模过程如下:
目标函数:使辛烷值损失最小,采用XGBoost的汽油辛烷值损失与主要操作变量的映射函数,用f(X)来表示,其中X=[X1,X2,X3,…,XM](M=25),代表影响汽油辛烷值损失的25个主要操作变量,并且下标与表2中的排序一一对应。
min(f(X))
(15)
硫含量的约束条件:利用XGBoost建立硫含量与25个主要操作变量的映射函数,即利用主要操作变量预测硫含量,用g(X)表示,并使得其质量分数不大于5 μg/g。
操作变量的约束条件:每个操作变量的取值范围如表4所示。于是,最终的优化模型如下:

表4 影响汽油辛烷值损失的25个主要操作变量的取值范围Table 4 25 main operational variables affecting RON loss
min(f(X))
(16)
4.2 改进的差分灰狼优化算法设计
对于优化问题,传统的数学规划方法在求解过程中难以实现全局最优,且收敛性差。目前,基于种群迭代的智能优化算法由于其较快的求解速率在工程上得到了广泛应用。灰狼优化(Gray Wolf Optimizer,GWO)[16]算法作为一种较新的智能优化算法,凭借其结构简单、需要调节的参数较少和较好的鲁棒性的特点,也得到了许多学者的关注。但是,与其他智能优化算法类似,基本的灰狼优化算法也存在着一些缺点,比如对于高维问题容易陷入局部最优、求解精度不高等。针对此问题,笔者提出了一种改进的差分灰狼优化算法来对模型进行求解。
4.2.1 基本灰狼优化算法
GWO算法是借鉴大自然中狼群捕食行为和社会领导阶层分工的思想而提出的一种新型智能优化算法。在一个小型灰狼群体中,有3个最优的个体,分别为α狼、β狼和δ狼,它们处于金字塔的上层,其他狼听从这些狼的指挥。
这些灰狼在追逐和包围猎物过程可以抽象为一个数学模型,提出了以下公式:
(17)
(18)
(19)

(20)
(21)
(22)
(23)
(24)
式中:umax为最大迭代次数;其他灰狼个体根据α、β和δ的位置分别更新各自的位置。
4.2.2 灰狼算法的改进策略
(1)基于sigmoid函数的收敛因子调整
根据前面灰狼算法的机理分析可知,A值的大小代表灰狼包围猎物时的范围,A越大说明包围圈越大,反之包围圈越小,即代表了灰狼的全局勘探和局部精细搜索的能力。而A的取值是随收敛因子a变化的。也就说明了收敛因子影响着灰狼算法的全局搜索和局部搜索能力。然而,在基本的GWO中,收敛因子是线性递减的,这种搜索策略在实际寻优过程难以适应实际情况。为了使得灰狼在开始阶段搜索的范围较广,并在结束阶段能够在很小的范围内进行精细搜索,采用sigmod函数来控制收敛因子的取值,可以使算法的全局勘探和局部搜索能力更强,其收敛因子的更新策略如公式(25)所示,采用这种策略,既有利于加快收敛速率,又能使算法在迭代末期获得最优值。
(25)
(2)基于差分变异策略的个体更新
在基本的GWO算法中,由式(24)可以看出,群体中其他灰狼个体的更新是由α狼、β狼和δ狼这3种狼的位置决定的。如果这3种狼陷入了局部最优解的周围,会导致其他狼的个体的多样性减少,从而使得算法出现早熟现象,无法跳出局部最优的包围圈,求解效果会变得较差。为了解决这一问题,可以引入变异操作算子,使得算法避免这种陷入局部最优的状况。常见的变异算子有高斯变异、柯西变异等。
受到差分进化算法的启发,笔者采用差分变异算子来对其他狼的位置进行调整。即利用当前灰狼个体、最优灰狼个体和随机选择的灰狼个体进行随机差分选择进行位置更新,其表达式如下:
(26)

4.2.3 改进差分灰狼优化算法的步骤

4.3 模型求解与结果分析
根据325个样本数据的操作变量的原始值,分别对改进的差分灰狼优化算法进行初始化,通过优化算法的不断迭代可以求解每个数据样本对应的主要变量优化后的操作条件。表5列出了第1个样本优化前后的操作变量和汽油辛烷值损失值的数据,同时还给出了硫含量的值。由表5可以发现硫质量分数在5 μg/g以下,满足国六车用汽油标准要求的硫含量取值范围。

表5 第1个样本操作变量和汽油辛烷值损失优化前后结果Table 5 Operation variables of the first sample and RON loss before and after optimization
为了进一步验证改进差分灰狼优化算法的效果,对数据集前325个样本优化前后的辛烷值损失值大小进行了可视化,如图7所示。由图7可知,325个样本中辛烷值损失值的初始值都较大,大部分超过了1,而优化后的值却在0.4上下波动,证明了改进的差分灰狼算法很大程度上降低了汽油辛烷值损失值,这进一步说明了所建立的模型和设计的算法的有效性。

图7 325个样本辛烷值损失值优化前后结果对比Fig.7 Result comparison before and after optimization of RON loss of 325 samples
除此之外,笔者还计算了优化后的汽油辛烷值损失值的降幅,其计算公式为:

采用上述公式对图7中所有样本的降幅进行了计算,表6给出了汽油辛烷值损失值降幅的区间范围。由表6可以看出,辛烷值损失降幅在30%以下的只有3个样本,大多数样本的损失降幅在60%~80%之间,这也证明优化的效果很好

表6 优化后的汽油辛烷值(RON)损失降幅分布Table 6 RON loss range after optimization
4.4 算法有效性分析
为了验证所提出的改进差分灰狼优化算法的有效性,分别与差分算法(Differential Evolution Algorithm,DE)和灰狼算法进行了对比,结果见图8。
本实验采用python编程实现,电脑的处理器为:AMD Ryzen 74800H with Radeon Graphics(2.90 GHz),内存(RAM)为16 GB,优化1个训练样本所花费的时间为28 s,效率比较高。
由图8可知,所提出的改进算法在收敛速率和求解精度上均是最优的,这进一步验证了算法的有效性。

GWO—Gray wolf optimizer;DE—Differential evolution algorithm图8 3种优化算法的迭代曲线Fig.8 Iterative curve diagrams of three optimization algorithms
5 结 论
基于机器学习算法XGBoost建立汽油辛烷值损失值与主要特征变量之间的映射函数,并提出一种改进的差分灰狼算法建立关于汽油辛烷值损失值最小的单目标优化模型,最终得出的结论如下:
(1)分别采用Pearson系数、最大互信息系数和随机森林特征选择法计算来筛选主要特征变量,并利用权重法对各特征重要度进行融合,有效避免了单一特征评价方法的局限性;
(2)采用XGBoost和多种流行的机器学习模型分别预测汽油辛烷值损失,其中XGBoost算法的RMSE值、MAE值和R2系数分别为1.3197、0.3581和0.9981,通过对比分析证明XGBoost算法的预测性能最佳;
(3)针对具有高维变量的优化问题,提出了一种改进的差分灰狼优化算法,利用该算法可以将数据样本的辛烷值损失降低至0.4左右。分别与差分进化算法和基本灰狼优化算法进行对比,发现改进的算法在求解速率和精度上有了一定的提升。
建立的降低汽油辛烷值损失模型可以尽量减少汽油精制过程中的辛烷值损失,为化工企业和运营商提供决策分析。但是此研究没有考虑到实际工业生产过程中汽油辛烷值损失预测的实时性,未来的研究可以围绕在线极限学习机模型对汽油辛烷值进行预测,以提高汽油的生产质量与效率。

