基于全生命周期与组合模型的蒸汽辅助重力泄油产油量与可采储量预测
余 洋,刘尚奇*,刘 洋,梁光跃,谢 佳
(1.中国石油勘探开发研究院,北京 100083;2.中国石油辽河油田分公司,盘锦 124010)
蒸汽辅助重力泄油(steam assisted gravity drain,SAGD)技术是一种用于开采超稠油油藏与油砂的行之有效的热采技术,通常情况下其采收率较蒸汽吞吐、蒸汽驱等常规热力采油方法更高,在中外已经实现了大规模的商业化应用[1-5]。在油藏开发方案优化与生产调控过程中,相应开采技术条件下的产油量及可采储量是十分关键的参数[6],而SAGD开发产油量主要通过产能公式[7-10]、油藏数值模拟等手段[9-10]进行预测,SAGD开发方式下的可采储量预测更是少见报道。
关于产能公式的研究中,Reis[7]基于线性几何的思路提出了一种计算SAGD产油量的解析公式,可用于预测SAGD开发方式下的峰值产油;Shi等[8]基于前人关于蒸汽腔形状为倒三角形的假设,推导出了考虑蒸汽腔前缘温度变化的SAGD产能公式;Igbokwe等[9]假设蒸汽腔形状为抛物线形,推导出SAGD产油量预测公式;王大为等[10]考虑油藏各向异性的影响,修正了前人推导出的产能公式。前人通过对假设条件的不断修正,使产能公式法预测出的产油量更为接近真实值。然而,虽然利用产能公式计算SAGD开发产油量较为简单,但相应计算参数,如蒸汽腔前缘移动速度等[11],通常难以取全、取准,且大部分产能公式为SAGD开发过程中的高峰产能公式,仅能预测某阶段的瞬态产能值,无法捕捉SAGD项目全生命周期的产量特征。
卢川等[12-13]利用油藏数值模拟方法分别预测了储层中存在高含水层或泥砾岩层时的SAGD产油量;Liu等[14]利用油藏数值模拟方法预测了注汽井采用多分支井型时的SAGD产油量;段永刚等[15]利用油藏数值模拟方法预测了不同EBIP厚度变化模式下的SAGD产油量。通过数值模拟方法预测SAGD的产量变化时可以考虑更贴合油藏实际的情况,且能刻画SAGD项目全生命周期的产油量变化特征,但研究结果的精度很大程度上依赖于油藏地质与流体参数测取的准确性及历史拟合的质量,且模拟计算通常耗时耗力,计算成本较高。此外,在预测SAGD开发方式下的可采储量方面,陈元千等[16]提出了递减常数法与截距除斜率法,这两种方法简单实用,但仅利用到产量递减阶段的数据,在此与所提出方法计算出的可采储量进行对比验证。
为研究多种全生命周期模型在SAGD开发方式下产油量及可采储量预测方面的适用性,提出了一种利用SAGD分段产能公式回归预测产油量及可采储量的新方法,并在上述研究的基础上提出了利用组合预测模型提高预测精度的思路,最后通过SAGD开发油藏的实际案例来验证每种方法的有效性与实用性。
1 全生命周期模型
典型SAGD开发油藏的产油量变化曲线如图1所示。可以看出,SAGD开发油藏的产油量变化可分为如下阶段[16-17]:①产量上升阶段:在该阶段中蒸汽腔以纵向扩展为主,但未到达油层顶部,产量快速上升;②相对稳定阶段与产量递减阶段:当蒸汽腔扩展到油藏顶部时,原油产量达到峰值,此时蒸汽腔从油藏上部开始向两侧横向扩展,该阶段原油产量相对平稳;③蒸汽腔继续沿横向扩展,当蒸汽腔在水平方向上延伸到一定程度后,蒸汽腔底部明显开始向下扩展,最终与相邻井对的蒸汽腔聚并、融合,在该阶段产量不断下降。
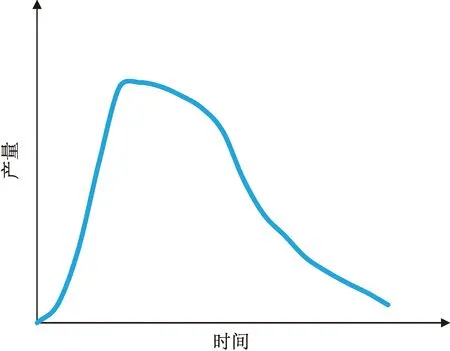
图1 典型SAGD开发油藏产油量变化示意图Fig.1 Schematic diagram of oil production change in a typical reservoir developed by SAGD process
SAGD开发油藏的产量变化与全生命周期模型中所描述的事物兴起、成熟至衰退的变化过程类似[18-20],因此考虑用广义翁氏模型与其他全生命周期模型来预测SAGD开发油藏的产油量与可采储量。这些方法可预测SAGD开发不同阶段的产油量变化,具有快速、准确及能拟合多种曲线形态等优点,并可预测SAGD开发油藏的可采储量。同时提出了一种利用SAGD分段产能公式回归的全生命周期模型来预测SAGD开发油藏的产油量与可采储量。
1.1 广义翁氏模型
翁氏模型描述的是事物从兴起、成长、成熟到衰退的全过程,与SAGD开发油藏的产油量变化十分相似,因此将广义翁氏模型应用于预测SAGD开发油藏的产油量及可采储量在理论上是可行的。根据广义翁氏模型[20-21],可推导出产量与时间的关系式以及可采储量的计算公式为
Q=a1tb1e-(t/c1)
(1)
式(1)中:Q为油藏年产油量,104m3/a;t为生产时间,a;a1、b1、c1为广义翁氏模型的模型常数。
NR=a1c1b1+1Γ(b1+1)
(2)
式(2)中:NR为可采储量,104m3;Γ(b1+1)为Gamma函数。
1.2 Rayleigh模型
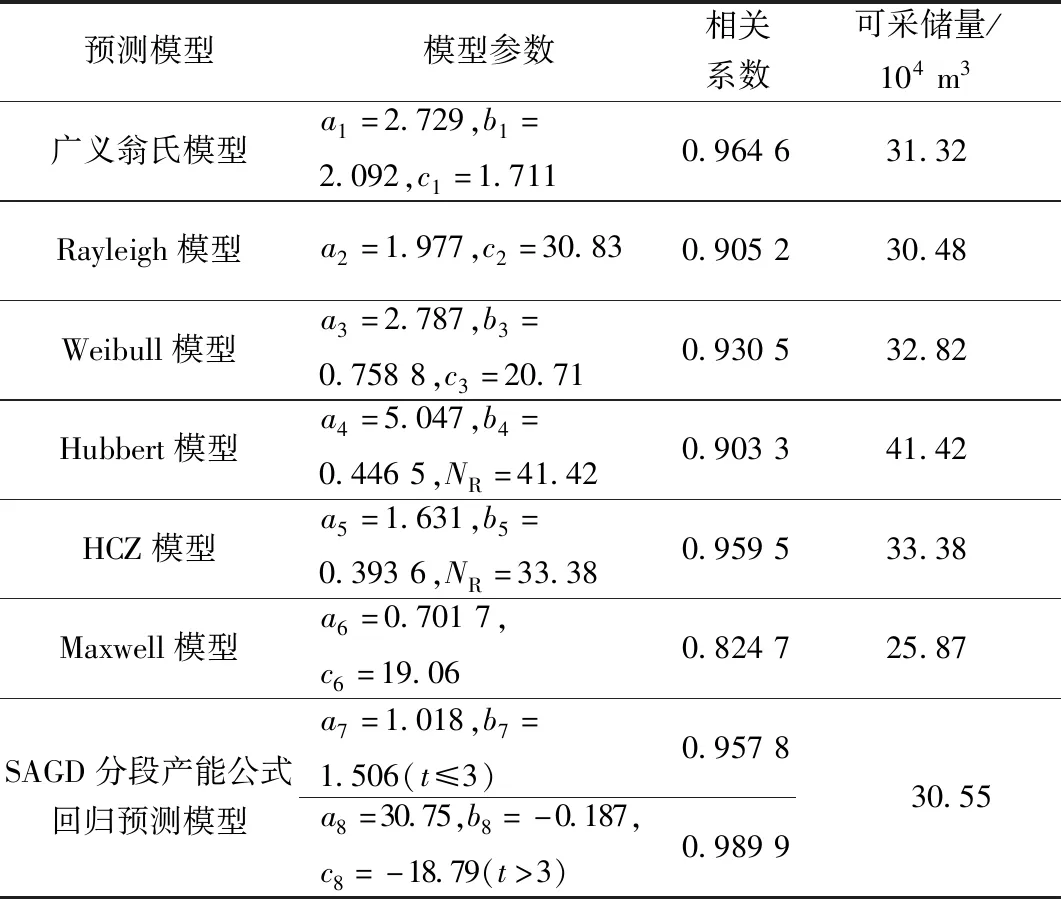
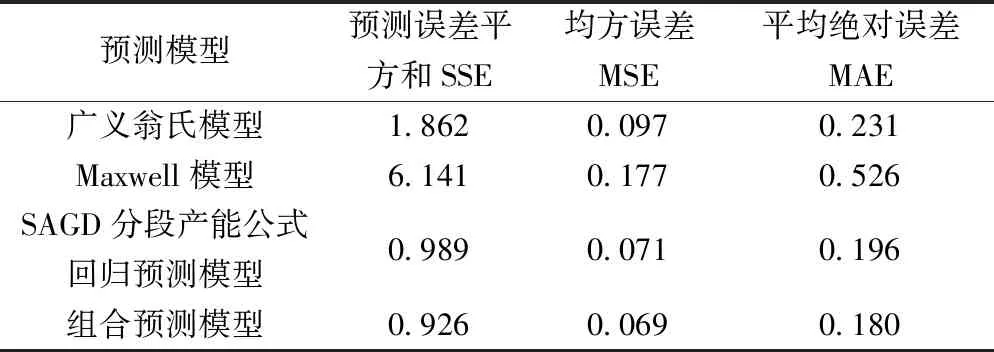
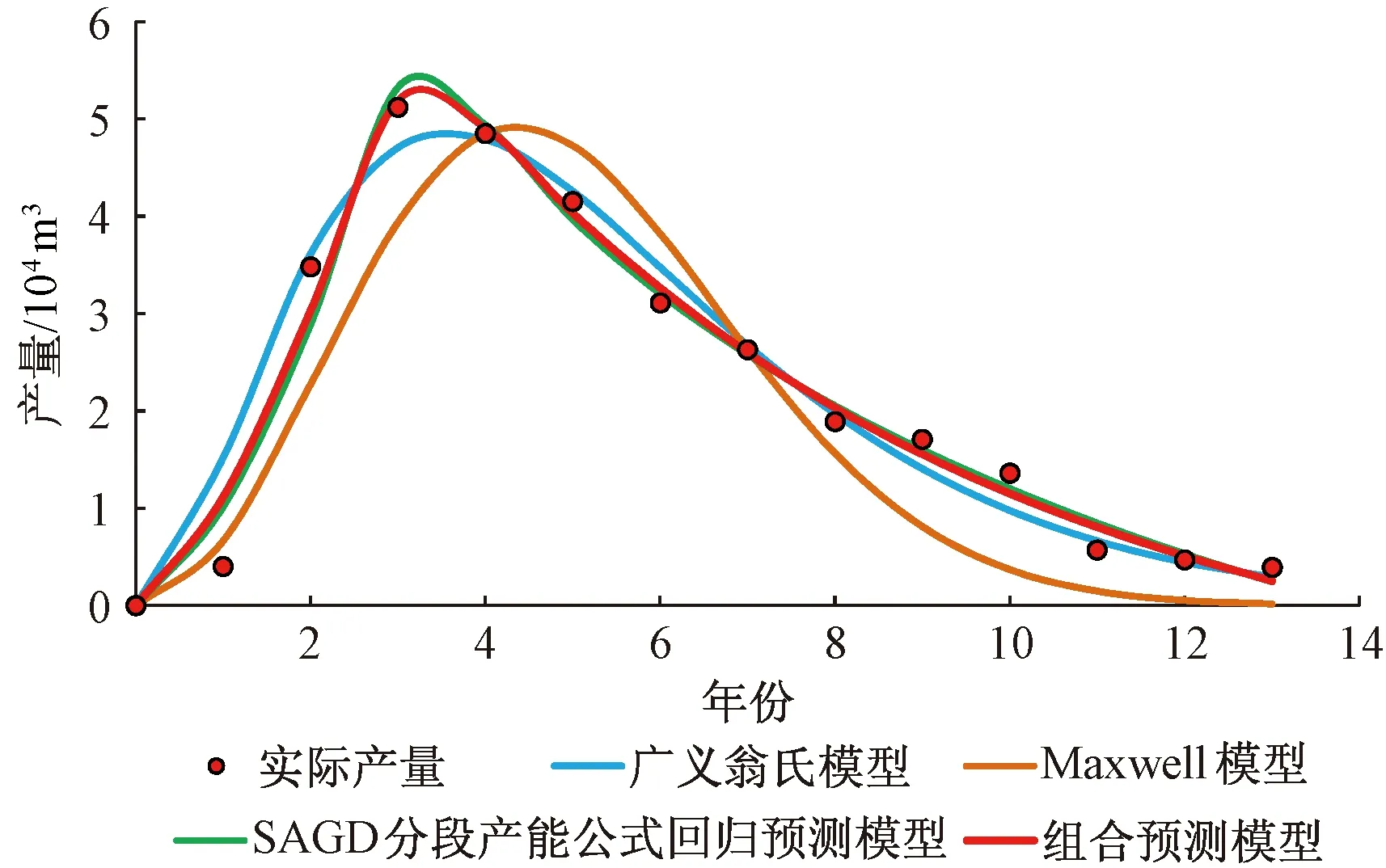
Rayleigh分布函数在随机变量0 Q=a2te-(t2/c2) (3) NR=0.5a2c2 (4) 式中:a2、c2为Rayleigh模型的模型常数。 Weibull分布是Weibull提出的统计分布模型,根据Weibull模型[23-25],可推导出产量与时间的关系式以及可采储量的计算公式为 Q=a3tb3e-(tb3+1/c3) (5) NR=a3c3/(b3+1) (6) 式中:a3、b3、c3为Weibull模型的模型常数。 Hubbert模型是一个随时间增长的模型,将其引入油气田开发,经推导后可以用来预测油藏产油量与可采储量等多项开发指标,根据Hubbert模型[21,26],可推导出产量与时间、可采储量的关系式为 Q=a4b4NRe-b4t/(1+a4e-b4t)2 (7) 式(7)中:a4、b4为Hubbert模型的模型常数。 HCZ模型为陈元千等[27-28]基于累积产油量随时间递增的信息特征,结合大量油气田的统计研究成果,推导建立的预测模型。根据HCZ模型,可推导出产量与时间、可采储量的关系式为 Q=a5NRe[-(a5/b5)e-b5t-b5t] (8) 式(8)中:a5、b5为HCZ模型的模型常数。 王昕等[29]基于概率统计中的Maxwell分布,建立了两参数的石油产量预测模型,根据Maxwell模型,可推导出产量与时间的关系式以及可采储量的计算公式为 Q=a6t2e-(t2/c6) (9) (10) 式(9)中:a6、c6为Maxwell模型的模型常数。 基于Miao等[30]的研究考虑水力压裂的低渗气藏产量递减预测时的思路,先找到能够描述SAGD开发油藏产量随时间变化的产能公式,再将其转换为可用于历史数据回归的关系式,该方法能在某种程度上捕捉SAGD开发过程中的物理特征,并且仅利用到生产数据,参数易于获取,简单实用。利用SAGD技术开发油藏时,不同开发阶段的产能计算公式不同,先推导出SAGD开发时不同开发阶段的产能公式[31-32],再将其转换为经验关系式,可表示为 (11) 式(11)中:a7、b7、a8、b8、c8为回归常数;tpeak为产量达到峰值的时间,a。 (12) 式(12)中:tend为产量递减为0或达到经济极限产量的时间,年。 由于实际情况较为复杂,预测环境也往往发生变化,通常情况下单项预测模型不能涵盖所需预测的所有情况,此时若仍采用单项预测模型,预测精度将受到影响。通过一定规则组合各单项预测模型,可通过包含更全面的预测信息从而提高预测精度[33-34]。 设t时刻SAGD开发的产油量真实值为qt(t=1,2,…,m),n种预测方法得到的n个模型的预测值为qit(i=1,2,…,n;t=1,2,…,m),第i种预测方法在第t时刻的预测误差为eit=qt-qit(i=1,2,…,n;t=1,2,…,m)。定义第i种预测方法的预测误差向量为 Fi=(ei1,ei2,…,ein)T (13) 误差矩阵e为 e=(F1,F2,…,Fn) (14) 误差信息矩阵En为 En=eTe (15) (16) 式(16)中:qpt为采用组合预测模型计算出的t时刻SAGD开发的产油量预测值;wi为第i种预测方法的权重;qit为第i种预测方法在第t时刻的产量预测值。 组合预测模型的误差平方和S为 (17) 式(17)中:eit为第i种预测方法在第t时刻的预测误差。 求取使得误差平方和S最小的权重向量组合W,该权重向量组合对应的组合预测模型即为最优组合预测模型。由此可知,最优组合预测模型的求解即为求解下述最优化问题。 (18) 求解上述最优化问题即可得到预测SAGD开发产油量的最优组合预测模型,最优组合预测模型对应的可采储量预测值为 (19) 式(19)中:wio为第i种预测方法的最优权重;NiR为第i种预测方法所预测的可采储量值,104m3。 利用文献[16]中给出的加拿大森科公司(Suncor)麦凯河 SAGD开发项目的实际生产数据为例进行实例分析。该项目从2002年开始采用双水平井SAGD的方式生产,其中平台B的地质储量为47.6×104m3,在第3年达到产量峰值。利用非线性拟合Levenberg-Marquardt方法求解各全生命周期模型,得到各模型参数、相关系数与可采储量(表1),不同预测模型的产油量预测结果对比如图2所示。可以看出,广义翁氏模型、HCZ模型与SAGD分段产能公式回归预测模型的预测效果较好。文献[16]中应用递减常数法预测得到的可采储量(技术可采储量)为32.76×104m3,应用截距除斜率法得到的可采储量为32.24×104m3,与广义翁氏模型、HCZ模型与SAGD分段产能公式回归预测模型等方法的预测值相近,表明部分全生命周期模型与所提出的SAGD分段产能公式回归预测模型都具有较好的实用性与可靠性。 表1 各模型参数、相关系数与可采储量Table 1 Relative parameters,correlation coefficient and recoverable reserves of each model 从图2可以看出,大多数模型在产量递减阶段的预测效果较好,而产量上升阶段的预测效果较差,大多数模型第1年的产量预测值与实际产量相比都发生了较大偏离。为了进一步提高预测精度,采用结合了多个单项模型的组合预测模型进行研究,以此分散单项预测模型特有的不确定性以减少总体的不确定性。在本例中,考虑组合整体预测效果较好的广义翁氏模型、SAGD分段产能公式回归预测模型以及第1年产量预测最为准确的Maxwell模型。根据前述单项模型的预测结果可得误差信息矩阵为 图2 不同预测模型预测结果对比Fig.2 Comparison of prediction results of different prediction models (20) 通过求解式(18)所述的最优化问题可得最优的权重向量组合为(0.200 0,0.007 8,0.792 2)T,则本例的最优组合预测模型为 qpt=0.2q1t+0.007 8q2t+0.792 2q3t (21) 式(21)中:q1t为采用广义翁氏模型计算出的t时刻SAGD开发的产油量预测值;q2t为采用Maxwell模型计算出的t时刻SAGD开发的产油量预测值;q3t为采用SAGD分段产能公式回归预测模型计算出的t时刻SAGD开发的产油量预测值。 最优组合预测模型对应的可采储量预测值为 NR=0.2N1R+0.007 8N2R+0.792 2N3R (22) 式(22)中:N1R为采用广义翁氏模型所预测的可采储量值;N2R为采用Maxwell模型所预测的可采储量值;N3R为采用SAGD分段产能公式回归预测模型所预测的可采储量值。 不同预测模型预测结果对比如图3所示。为了更直观地对比各模型预测效果的好坏,采用3种常用的误差指标度量各模型预测结果的准确度,计算结果如表2所示,可以看出,组合预测模型的各项误差指标均为最小,相较于单项预测模型预测精度得到了进一步提高。通过组合预测模型计算出的可采储量为30.67×104m3,用该值除以对应的地质储量,可得到平台B单元的采收率为64.4%。 表2 不同预测模型的精度指标比较Table 2 Precision index comparison of different prediction models 图3 4种预测模型预测结果对比Fig.3 Comparison of prediction results by four prediction models (1)SAGD开发方式下的产量变化与前人提出的全生命周期模型的变量变化过程类似,因此广义翁氏模型、Rayleigh模型、HCZ模型等全生命周期模型可以应用于预测SAGD开发的产油量及可采储量;对于文中实例,广义翁氏模型的预测效果最好。 (2)基于SAGD不同开发阶段的产能计算公式,提出了一种SAGD分段产能公式回归预测模型,该方法可较好的应用于预测SAGD开发油藏的产油量及可采储量,方法简单实用,预测精度较高。 (3)在通过多方法进行加权组合时,可利用多方法的预测误差平方和最小为准则确定最优权重向量,组合预测模型可捕捉到更多的变量信息,相较单项预测模型能够进一步提高预测精度,应用效果较好;对于文中实例,通过组合预测模型计算出的可采储量为30.67×104m3,用该值除以对应的地质储量,可得到平台B的采收率为64.4%,这是评价SAGD开发效果的一个重要指标。1.3 Weibull模型
1.4 Hubbert模型
1.5 HCZ模型
1.6 Maxwell模型
1.7 SAGD分段产能公式回归预测模型
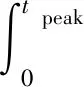
2 组合预测模型
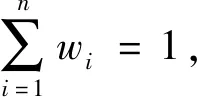
3 实例分析

4 结论