基于采掘应力增量的瓦斯压力演化规律研究

张士岭

(1.瓦斯灾害监控与应急技术国家重点实验室，重庆 400037；2.中煤科工集团重庆研究院有限公司，重庆 400037)

煤与瓦斯突出动力灾害一般发生在采掘作业过程中，采掘作业产生的应力集中及高压瓦斯成为突出动力灾害的重要诱因。受采掘影响，煤体原岩应力和瓦斯渗流平衡被打破，引起煤体应力重新分布及瓦斯压力变化。谢广祥等[1]通过现场实测研究表明，煤层瓦斯压力与采掘附加应力呈“双增”趋势变化，瓦斯压力峰值超前于采掘应力；吴胜[2]、张毅[3]研究认为瓦斯压力随采动应力增大先升高后降低；胡祖祥等[4]研究认为在采动影响下瓦斯压力峰值与采动应力变化不同步；张东明[5]、侯芳芳[6]等通过实测发现工作面瓦斯压力与采掘应力具有正相关性；马海峰[7]、尹光志[8]、彭守建[9]等研究认为瓦斯压力受控于采掘应力的变化。上述研究大多从定性的角度描述采掘应力与瓦斯压力之间的耦合作用关系，笔者基于土力学渗流固结理论，研究两者相互作用的受力过程，建立瓦斯压力受控于支承压力的力学模型，以期揭示采掘应力对瓦斯压力的控制机理。

1 采掘应力下瓦斯与煤体骨架的受力过程及模型建立

井下煤岩体在受采掘作业影响之前或采掘影响时间足够长后，煤体瓦斯呈静止或稳定流动状态，此时的瓦斯压力称为静瓦斯压力。受到采掘影响后，煤体中的瓦斯压力平衡或稳定渗流状态被打破，由于受到采掘产生的附加应力影响，孔隙瓦斯压力也会产生一定变化。笔者所述附加应力为采掘活动导致的应力增量。同样定义由采掘附加应力引起的瓦斯压力增大或减小部分为超静瓦斯压力，用Δp表示:

Δp=p-p0

(1)

式中:p为采掘后的瓦斯压力，MPa；p0为采掘前的瓦斯压力，MPa。

假设煤体上覆岩层中的压力由煤体骨架和瓦斯共同承担,煤体骨架承担的那部分为有效应力[10]。为形象地描述在附加应力作用下，瓦斯与煤体骨架的受力过程及相互作用大小，借鉴土力学太沙基渗流固结力学模型[11]，设计试验装置，如图1所示。该装置由充满气体的钢筒、带有微小排气孔道(微孔隙)的活塞、支撑活塞的弹簧组成。弹簧模拟煤体骨架；钢筒中气体模拟煤体中的瓦斯；活塞中的微孔隙模拟煤体的渗透性。

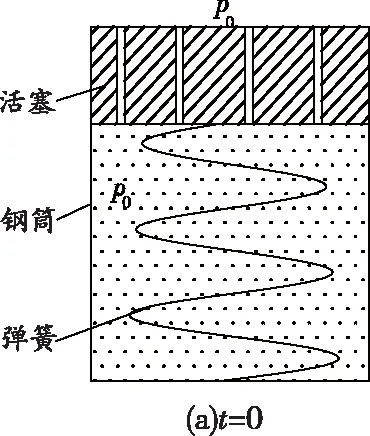
图1 采掘应力下孔隙瓦斯与煤体骨架受力试验模型

当活塞上没有荷载时，如图1(a)所示，弹簧受力为0(忽略活塞的质量及活塞与钢筒摩擦力)，钢筒内部的瓦斯压力为p0，由于外部空气压力也为p0，因此活塞微孔隙内没有渗流发生(忽略气体扩散)。

当在活塞上施加瞬时作用荷载σ时，即t=0时刻(见图1(b))，容器内的气体和弹簧瞬时被压缩。由于模拟煤体渗透性的活塞微孔孔径很小，且气体具有一定的黏滞性，钢筒内的气体来不及排出，相当于这些微孔被瞬时堵塞而处于不排气状态。由于容器内弹簧和气体同时被压缩，因此附加荷载由弹簧(煤体骨架)和气体共同承担，气体的压力上升到pt=0，弹簧(煤体骨架)上的应力增大到σ′t=0，且弹簧的体积压缩量和气体相同。因此由外荷载引起的超静瓦斯压力Δpt=0=pt=0-p0;作用于弹簧上的应力增量为σ′t=0。

当t>0时，例如t=ti时(见图1(c))，由于活塞两侧存在压力差，将有气体渗流发生，瓦斯从活塞的微孔隙中不断流出，活塞往下移动，其下方的瓦斯不断减少，代表煤体骨架的弹簧进一步被压缩，部分荷载转移到弹簧上(σ′t=ti)。同时，容器内的瓦斯压力减小为pt=ti。由竖向的受力平衡可知：Δpt=ti+σ′t=ti=σ。

当上述过程持续的时间足够长,即t=t∞时(见图1(d))，容器内的超静瓦斯压力完全消散，Δpt=t∞=0，活塞内外压力达到平衡，钢筒内的瓦斯压力又恢复到原始状态p0，渗流停止。全部荷载都由弹簧承担，即弹簧应力增量为σ′=σ。

上述过程形象地模拟了煤体在采掘应力作用下煤体骨架与孔隙瓦斯的受力变化过程。在这一过程中，煤体中的超静瓦斯压力不断消散，外荷载逐步转移到煤体骨架上，煤体有效应力逐渐增大，同时煤体微孔隙被压缩。

通过上述研究，可得到如下认识：

1)在采掘应力作用过程中，超静瓦斯压力Δp与煤体有效应力增量σ′都是时间的函数。若采掘应力为σ，则始终有Δp+σ′=σ。采掘应力作用过程就是2种不同应力形态不停的转化过程。

2)上述由附加荷载引起的瓦斯压力增量称为超静瓦斯压力。超静瓦斯压力由外部作用(采掘附加应力)所引起，其不同于静瓦斯压力，而是随时间变化的。显然在t=0时，即采掘应力刚发生时，超静瓦斯压力达到最大，意味着煤体瓦斯压力此刻达到峰值。

2 超静瓦斯压力系数

在采掘附加应力作用下，瓦斯压力将产生多大的增量，煤体中产生多大的超静瓦斯压力，以及煤体应力如何变化，是涉及煤岩动力灾害发生的十分重要的问题。为进行上述研究，做出如下假设：

1)煤体均质同性，作用在煤体上的采掘附加应力保持不变；

2)忽略煤体瓦斯的吸附或解吸，以及瓦斯压力增量对煤体骨架体积应变的影响。

根据前述研究可知，在t=0时，由于气体来不及排出，附加应力产生的超静瓦斯压力达到最大。为研究此刻的采掘应力对瓦斯压力的影响规律，定义在不允许煤体孔隙流体进出的情况下，由附加应力引起的超静瓦斯压力与附加应力(总应力增量)之比为超静瓦斯压力系数ξ。

根据弹性力学理论，在轴对称应力状态下的主应力可表示为矩阵形式，并可分解为[12]：

(2)

式中：σ1、σ3分别为最大、最小主应力，MPa；等式左侧表示轴对称应力状态；等式右侧第一项表示煤体单元3个方向上的主应力相等，称为等围压应力状态或球应力分量；等式右侧第二项为偏差应力分量。

2.1 等围压应力状态下超静瓦斯压力系数

首先分析等围压应力状态下的瓦斯压力变化情况。在不排气的条件下，施加球应力分量的增量Δσ3，会在煤体中产生有效应力增量Δσ′3和瓦斯压力增量Δp1。竖直方向的受力平衡方程如下：

Δσ3=Δσ′3+Δp1

(3)

其中Δσ′3作用于煤体骨架上，Δp1作用于煤体孔隙瓦斯流体上。

煤体骨架在有效应力增量Δσ′3作用下，煤体骨架体积压缩量为[11]：

ΔVs=CsV0Δσ′3=CsV0(Δσ3-Δp1)

(4)

式中：ΔVs为煤体骨架体积压缩量，m3；Cs为煤体骨架的体积压缩系数，MPa-1；V0为煤体单元的初始体积，m3。

孔隙中的瓦斯本身也会被压缩，在瓦斯压力增量Δp1作用下，其压缩量ΔVg为：

ΔVg=CgVgΔp1=qCgV0Δp1

(5)

式中：Cg为瓦斯的体积压缩系数，MPa-1；Vg为煤体单元孔隙的总体积，m3；q为煤体的孔隙率。

假设煤体颗粒本身不可压缩，煤体骨架被压缩必将导致孔隙减少。孔隙的减少有2种原因：①孔隙中瓦斯气体被挤压排出；②孔隙流体本身被压缩。在不排气的条件下，只能是孔隙流体本身被压缩。煤体的压缩量等于煤体骨架的体积压缩量，同时等于孔隙中瓦斯的体积压缩量，即ΔVs=ΔVg。式(4)和式(5)相等,整理得到：

(6)

对于气体瓦斯，由于Cg/Cs≫1，因此式(6)可以简化为：

(7)

令ξ1=Cs/qCg，式(7)可改写为：

Δp1=ξ1Δσ3

(8)

式中ξ1为各向等压条件下的超静瓦斯压力系数，表示单位球应力分量的增量引起的超静瓦斯压力增量。

超静瓦斯压力系数与煤体骨架体积压缩系数、气体压缩系数的比值有关，还与孔隙率有关。对于井下煤体，其骨架体积压缩系数很小，而气体的压缩系数相对较大，因此ξ1值较小。

2.2 偏差应力状态下超静瓦斯压力系数

根据式(2)，σ3不变，只施加偏差应力增量Δ(σ1-σ3)，在不排气条件下，将产生瓦斯压力增量Δp2,这需要另一个超静瓦斯压力系数来表述。在Δp2作用下，瓦斯的体积压缩量为：

ΔVg=CgVgΔp2=qCgV0Δp2

(9)

假设煤体骨架为弹性体，则体积变化可以通过广义胡克定律计算[13]，煤体骨架体积变化为：

ΔVs=εV0=(ε1+ε2+ε3)V0

(10)

(11)

式中：ε为煤体骨架体积应变；ε1、ε2、ε3分别为煤体骨架3个方向的线应变；Δσ′1、Δσ′2、Δσ′3分别为煤体骨架3个方向的应力增量，MPa；E为煤体弹性模量,MPa；ν为泊松比。

施加偏差应力增量Δ(σ1-σ3)以后，煤体骨架与瓦斯压力轴向、侧向的应力增量如表1所示。

表1 瓦斯压力与煤体骨架应力增量

根据广义胡克定律，将表1应力代入式(11)得轴向应变ε1、侧向应变ε2、ε3，然后将其代入式(10)得：

ΔVs=(1-2ν)[Δ(σ1-σ3)-3Δp2]V0/E

(12)

由

Cs=E/3(1-2ν)

(13)

则式(12)变为:

(14)

在不排气的条件下，煤体骨架的压缩量应等于孔隙内瓦斯的体积压缩量，可以得到：

(15)

由式(15)可知，在煤体的弹性假设下，由单位偏差应力引起的瓦斯压力增量为ξ1/3。

因此在轴对称应力状态下，瓦斯压力的增量为：

(16)

采掘工作面前方应力区可分为减压区、增压区、稳压区。减压区内应力小于原岩应力；稳压区内煤体应力接近于原岩应力，采掘附加应力较小，对瓦斯压力影响有限[14-15]。显然增压区是采掘应力影响瓦斯压力的主要区域，增压区内实际施加的采掘应力在3个方向上是不相等的，沿工作面倾向和垂直方向应力较大，而回采(掘进)方向应力较小[16-17]。因此在使用上述模型时，需对工作面前方应力进行一定的简化：假设沿工作面倾向和垂直方向应力相等，并忽略水平剪应力，从而将工作面倾向、回采方向、垂直方向的正应力看作主应力。因此，在工作面采掘应力作用下瓦斯压力增量可表示为：

(17)

式中：σy为工作面切向支承压力，MPa；σx为工作面回采(掘进)方向应力，MPa。

由于增压区内煤体沿工作面切向应力一般远大于工作面回采(掘进)方向应力，且切向应力前面系数为后者的2倍，因此忽略工作面回采(掘进)方向应力对瓦斯压力增量的影响，并令ξ=2ξ1/3，式(17)可简化为：

Δp=ξσy

(18)

式中ξ为超静瓦斯压力系数，ξ=2Cs/3qCg。

由式(18)可知，超静瓦斯压力与煤体支承压力呈正比关系，比例系数ξ即为超静瓦斯压力系数。综上分析，通过一个简洁的方程能将超静瓦斯压力与煤体支承压力联系起来。

3 模型验证及应用

谢广祥等[1-2,4-5]通过现场实测、实验室试验，对工作面煤层瓦斯压力和采动应力的耦合作用进行了研究。为了验证上述理论公式的正确性，取文献[1-2,4-5]中关于采动应力增量对应的有代表性的瓦斯压力增量试验数据，并与本文超静瓦斯压力系数计算模型进行对比，结果如表2所示。根据文献[18-20]，取Cg=0.27 MPa-1,Cs=3.6×10-4MPa-1,q=10%,代入式(18)可得超静瓦斯压力系数ξ=8.89×10-3。

表2 模型计算结果与相关文献数据对比

由表2可知，瓦斯压力增量模型计算结果与文献实测结果的绝对误差为-0.190～0.040 MPa，相对误差为-58.40%～32.00%，其中大部分计算结果与文献数据吻合较好，误差绝对值小于20%，少部分结果误差较大，绝对值超过40%。总体上看，超静瓦斯压力模型计算结果与实际测量结果基本吻合，证明模型的合理性。

由式(18)可知，超静瓦斯压力受控于采动附加应力，随着采掘支承压力增大，瓦斯压力亦增大，表明两者具有正相关的耦合效应，得到与文献[1，5-6]相一致的结论。根据文献[1，4]还知瓦斯压力峰值位置超前于采动应力峰值。由前述试验分析可知，采动附加应力刚作用时引起的瓦斯压力增量最大，即瓦斯压力此刻达到峰值，对应产生的煤体有效应力增量最小；而随着时间的增加，在瓦斯压力梯度下，煤体发生瓦斯渗流：从增压区流向减压区，超静瓦斯压力不断下降，采动应力逐步转移至煤体骨架上，导致煤体有效应力不断增加并达到峰值。这就从理论上解释了瓦斯压力峰值位置超前于采动应力峰值的现象。

4 结论

1)超静瓦斯压力是由采掘附加应力引起的瓦斯压力增大或减小部分；超静瓦斯压力系数为在不允许煤体孔隙流体进出的情况下，单位附加应力增量引起的超静瓦斯压力增量。在采掘应力作用过程中，超静瓦斯压力Δp与煤体有效应力增量σ′都是时间的函数，并始终有附加应力等于超静瓦斯压力Δp与煤体有效应力增量σ′之和。

2)采掘应力作用过程就是2种不同应力形态不停的转化过程：采掘应力刚发生时，超静瓦斯压力达到最大，随着渗流的进行，超静瓦斯压力不断消散，附加应力逐步转移到煤体骨架上，煤体有效应力增大。超静瓦斯压力与煤体支承压力呈正比关系，比例系数即超静瓦斯压力系数与煤体骨架体积压缩系数呈正比关系，与孔隙率、瓦斯体积压缩系数呈反比关系。