应用磁流变阻尼器的车辆半主动座椅悬架系统性能研究

沙树静，王中男，杜海平

（1.长春工业大学机电工程学院，吉林 长春 130012；2.伍伦贡大学电子计算机与电子通信工程学院，澳大利亚 伍伦贡 新南威尔士 2522）

1 引言

磁流变液（Magnetorheological Fluids，简称为MRF）是一种由磁性粒子均匀分布在基液（母液）中构成的混合物，改变外加磁场可以控制其表观粘度且具有可逆性[1]。磁流变阻尼器以磁流变液为工作介质为阻尼器提供阻尼[2]，当阻尼器的励磁线圈中通入电流时，其产生的磁场会对工作区域内磁流变液产生作用使其表观粘度发生变化即流变效应，产生阻尼力。因此，欲得到目标阻尼力只需调节流过励磁线圈中电流大小即可。近年来，汽车工业的发展尤为迅速，这也使得人们对于车辆的舒适性与安全性的要求不断提升，而传统的被动座椅悬架因其响应效果差、响应速度慢，已无法满足人们的要求[3]。因此，寻找一种新式座椅悬架尤为重要。磁流变阻尼器具有诸多优点，例如能耗小，只需几安培电流即可获得较大的阻尼力，由电磁场控制，响应速度快、控制方便，并且无需复杂的机械结构即可与车辆电控系统相集成，因此利用磁流变阻尼器设计一种具有可调阻尼的半主动座椅悬架可用于改善车辆的乘坐舒适性与安全性[4]。磁流变阻尼器的阻尼力主要由其中的磁流变液的流变反应得到，而流变性主要受励磁电流产生的电磁场控制[5]。因此，合理的控制策略可以极大的提高座椅悬架的响应速度以及减振性能。PID控制器是一种比较传统的控制器其控制结构相对简单，运算速度快，鲁棒性强，被广泛应用于各种控制场合。但车辆在行驶过程中，所遇到的路面状况复杂，单一的PID控制无法满足悬架系统的减振需求。

采用七自由度人-座椅-车系统模型，采集偏差信号并利用BP神经网络的学习功能，在线整合PID控制策略的控制参数[6]，使得座椅悬架控制系统能够根据路况自适应调节励磁电流的大小，使得磁流变阻尼器的阻尼力随路况变化，从而改变系统阻尼系数，进而达到自适应控制的目的。

2 磁流变阻尼器工作原理与仿真模型

2.1 磁流变阻尼器结构与工作原理

能够阻碍自由振动并将振动能量逐步消耗掉的装置称为阻尼器，传统阻尼器主要由弹簧及其他摩擦元件组成，其阻尼参数是固定的。新型磁流变阻尼器利用工作区域内的磁流变液在磁场下的流变效应提供所需的阻尼力，其性能稳定、控制方法简单，广泛应用于各种机电设备中。其结构，如图1所示。

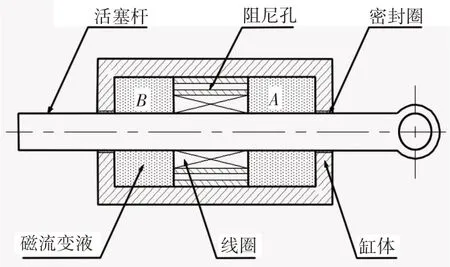
图1 磁流变阻尼器基本结构图Fig.1 Basic Structure Diagram of Magnetorheological Damper

磁流变阻尼器主要由活塞杆（用于阻尼力输出）、缸体、线圈（用于产生可控磁场）、阻尼孔（产生阻尼力）等结构组成。

磁流变阻尼器的缸体被分成A、B两个腔室，并在两个腔室中添加磁流变液，当活塞杆与缸体之间发生相对移动时，A、B两腔室产生压力差从而使得其中的磁流变液在压力作用下通过阻尼孔流动。

当线圈中无电流通过时，磁流变液的流动性很强，通过阻尼孔时所受阻碍作用小，仅是磁流变液自身的粘度阻碍其通过阻尼孔，此时，磁流变阻尼器产生的阻尼力很小。

当线圈中通入电流后，产生的磁场作用于磁流变液使其表观粘度发生巨大变化，其内部的磁性粒子聚集成链，此时磁流变液具有较大的剪切屈服强度，当其通过阻尼孔时会受到较大阻碍而影响活塞杆的运动，从而达到提供阻尼力的目的。

随着电流的增大阻尼力也在随之增大，由于磁流变液自身的励磁特性，其阻尼力与电流之间呈现出非线性的关系，可利用非线性数学模型描述。

2.2 磁流变阻尼器力学模型

根据对阻尼器的动态性能的描述主要将磁流变阻尼器的力学模型分为以下几种；Bingham模型、Bouc-wen模型、双曲正切模型等[7]。综合几种力学模型以及车辆行驶过程中所受的振动频率与幅值，Bingham模型与双曲正切模型难以应用于座椅悬架的仿真建模中，而Bouc-wen模型能够考虑低速时阻尼力与相对速度之间的滞环特性，并能准确地表达电流与阻尼力的非线性关系，因此这里采用Bouc-wen对座椅悬架进行仿真研究[8]。Bouc-wen模型，如图2所示。

图2 Bouc-wen模型Fig.2 Bouc-wen Model

式中：I—励磁电流。

利用MATLAB/Simulink 工具箱对磁流变阻尼器进行建模仿真，模型，如图3所示。

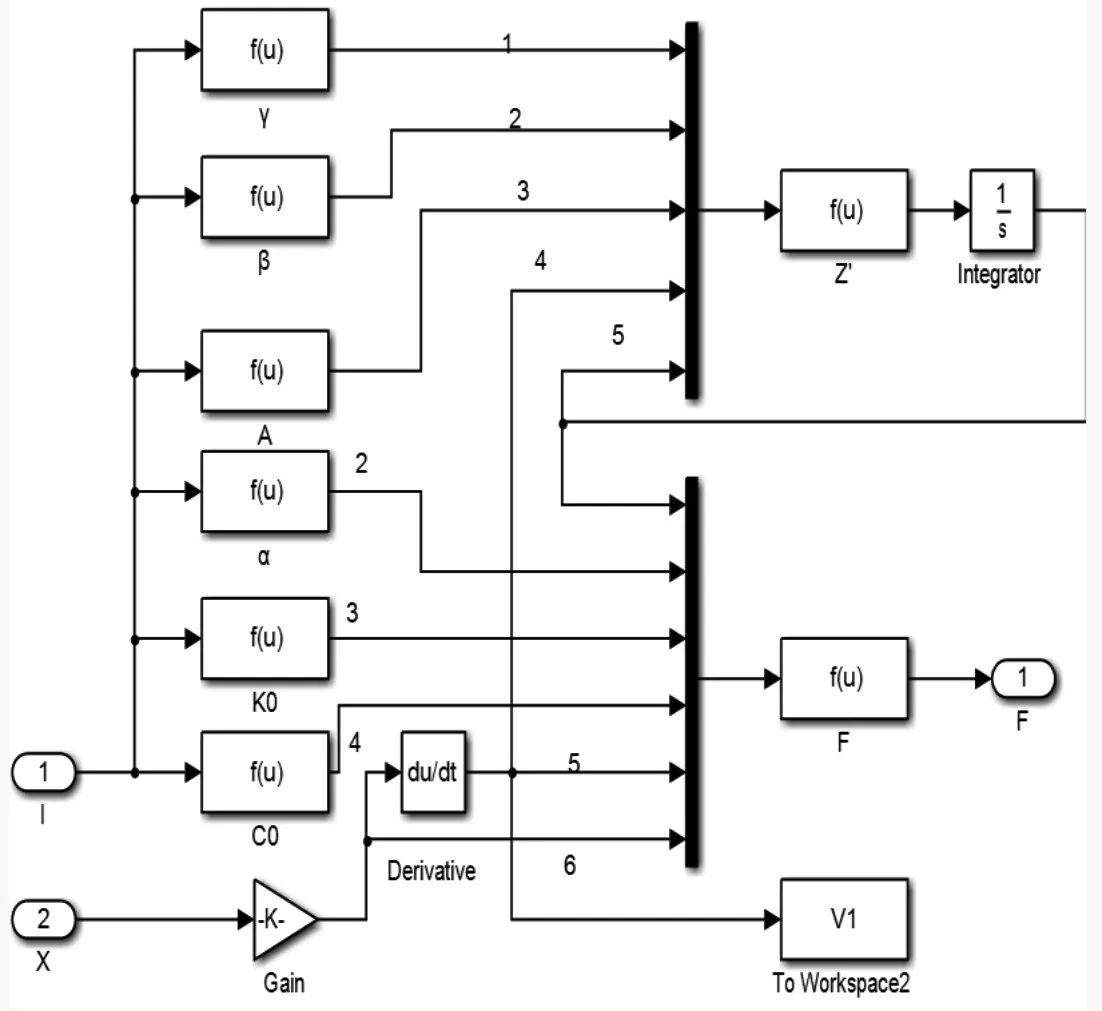
图3 Bouce-wen 仿真模型Fig.3 Bouce-wen Simulation Model

采用幅值为15、频率为2Hz的正弦激励，验证模型在电流分别为0A，0.5A，1A，2A，2.5A，3A时的位移与阻尼力关系及速度与阻尼力关系，如图4、图5所示。

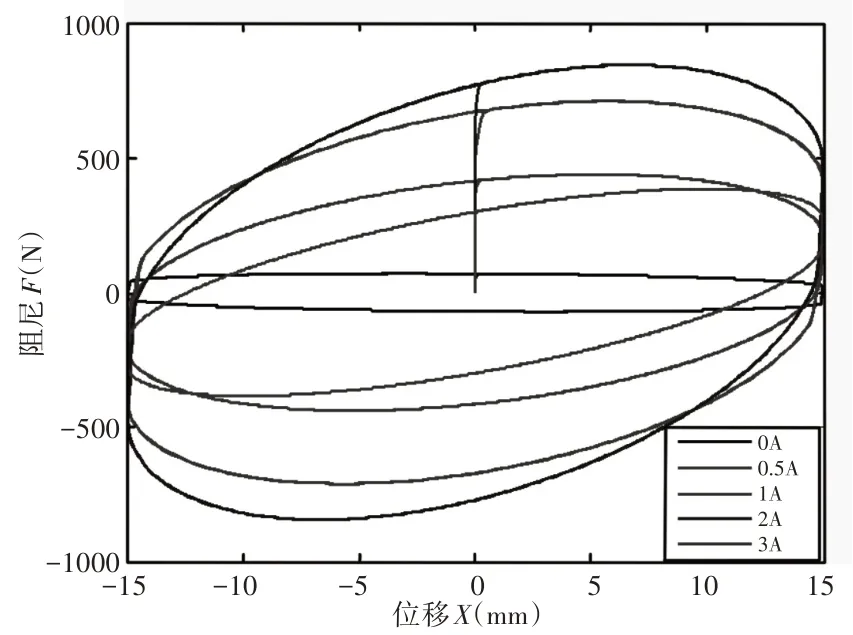
图4 阻尼力-位移关系曲线Fig.4 Friction Force-Displacement Relationship of Magnetorheological Damper

图5 阻尼力-速度关系曲线Fig.5 Friction Force-Velocity Relationship of Magnetorheological Damper

3 人-座椅-车辆与路面激励模型

3.1 人-车-座椅模型

这里选用七自由度人-座椅-车辆模型[9]，如图6所示。

图6 人-座椅-车辆模型Fig.6 Human-Seat-Vehicle Model

图中，将驾驶员身体分为四个系统，头部质量m4头部位移Z4，上身质量m3上身位移Z3，下身质量m2下身位移Z2，腿部质量m1腿部位移Z1。其中fr为磁流变阻尼器输出的可控阻尼力。其余参数，如表1所示。

表1 人-座椅-车模型参数表Tab.1 Parameters of Driver-Seat-Vehicle Model

根据牛顿第二运动定律及力学平衡条件方程，可得座椅动态平衡方程如下：

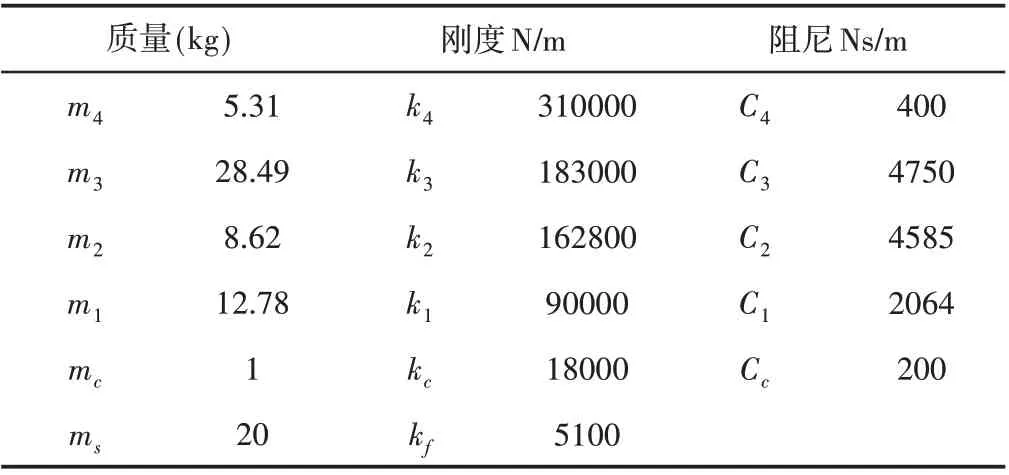
表2座椅模型参数值表Tab.2 Model Parameter Values

将各个参数值代入式（3）～式（9），并在Simulink中搭建出座椅悬架系统仿真模型。

3.2 路面激励模型

这里采用文献[10]用的线性滤波法，通过对确定频率的高斯白噪声通过滤波器进行适当的变换，从而得到具有一定谱特征的路面不平整度激励模型。

其中，对于参考空间频率n0，这里取n0=0.1m-1，对于路面不平整系数G(n0)这里取C 级路面G(n0)=256m2/m-1，v—速度取20m/s；ω(t)—高斯白噪声信号；f0—下限截止频率这里取0.1；q(t)—路面激励的幅值[11]。

利用MATLAB 中的Simulink 工具箱搭建出仿真模型，运行仿真程序得出路面仿真曲线，如图7所示。

图7 路面仿真曲线Fig.7 Curve of Pavement Simulation

4 控制策略设计

4.1 PID控制系统

PID控制器是经典控制理论之一，具有较长的发展历史[12]，PID控制器在结构上简单易于实现，仅需要通过PID的三个参数P（比例）、I（积分）、D（微分）进行调整就可以达到减小误差的目的，抗干扰能力强，在控制系统中可以得到良好的控制效果，因而广泛应用于工业控制中。传统PID控制器采用偏差信号e并以此作为输入量进行比例（P）、积分（I）、微分（D）计算，并将其进行线性组合得到输出的控制律u。PID控制系统在设计过程中最重要的就是寻找合适的参数值。

在实际控制系统中需要根据实际的误差响应曲线来增大或减小相应控制参数从而满足控制需要。

PID控制器各控制部分的作用：

（1）比例部分

比例部分能够对控制系统的偏差信号进行及时反映，一旦产生偏差，立即对控制器进行控制，使得偏差迅速降低。

（2）积分部分

进行积分运算的目的在于对系统静态误差进行消除从而保证系统从一个稳态进入下一个稳态具有较小的偏差，从而保证系统准确度[13]。

（3）微分部分

微分部分可以体现偏差的变化率，并且对偏差信号的增大较为敏感，提前加入修正量可以使控制器的灵敏度提升从而减少调节时间，减小系统输出在目标值附近的振荡。

经典PID控制器调整步骤如下：

①首先只考虑P（比例）环节对控制系统的影响，将系数KP从小逐渐增大，观察控制效果，而当比例系数KP过大时，系统会出现超调，此时减小系数至最佳值得到系统快速响应且超调较小的响应曲线。

②加入积分环节作用，步骤①中获得的KP比例系数不变，选取较小的KI微分环节系数，逐步增加该系数的值，观察响应曲线。使得系统不仅能够保持良好动态性能而且能够消除静态误差，同时微调两个参数从而获得最优的控制效果。

③在步骤②得到的参数的基础上加入微分环节的作用，先取得较小的KD（微分）环节系数，观察响应曲线，同时微调三个参数，得到最佳的响应曲线。经过多次的实验调整最终当PID控制策略的三个参数值分别为，KP=85.5，KI=52.5，KD=10.5时所获得的控制效果最好。

4.2 BP神经网络数学模型

Rumelhart等人于1986年提出一种收敛速度快，且容易求解的BP（Back Propagation）神经网络控制算法。

BP神经网络主要由输入层，隐含层，输出层三部分构成[14]，其运算过程包括信号前向计算和误差反向传播两个部分[15]。

网络结构，如图8所示。

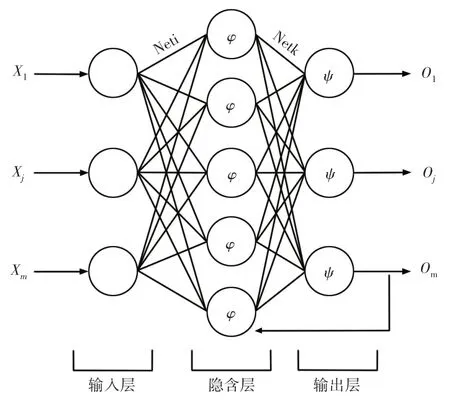
图8 神经网络结构图Fig.8 Neural Network Structure

设输出层权值修正量为Δωki，隐含层修正量为Δωij，学习速率本文取0.15。

4.3 BP神经网络整合PID控制策略

由于传统的PID 控制需要对PID 各个参数进行确定，耗时长，在应用于座椅悬架控制时，固定不变的参数很难适应多种不同的复杂路况。

BP神经网络可以通过采集误差信号，对权值进行修正从而改变输出值。

因此，考虑将BP神经网络与传统PID结合，利用实际系统输出值与期望值之间的误差进行运算，并根据系统当前的状态经BP神经网络的自适应功能在线整合PID 各个参数，使得座椅悬架能够达到最优的性能指标。

BP神经网络PID控制结构框图，如图10所示。

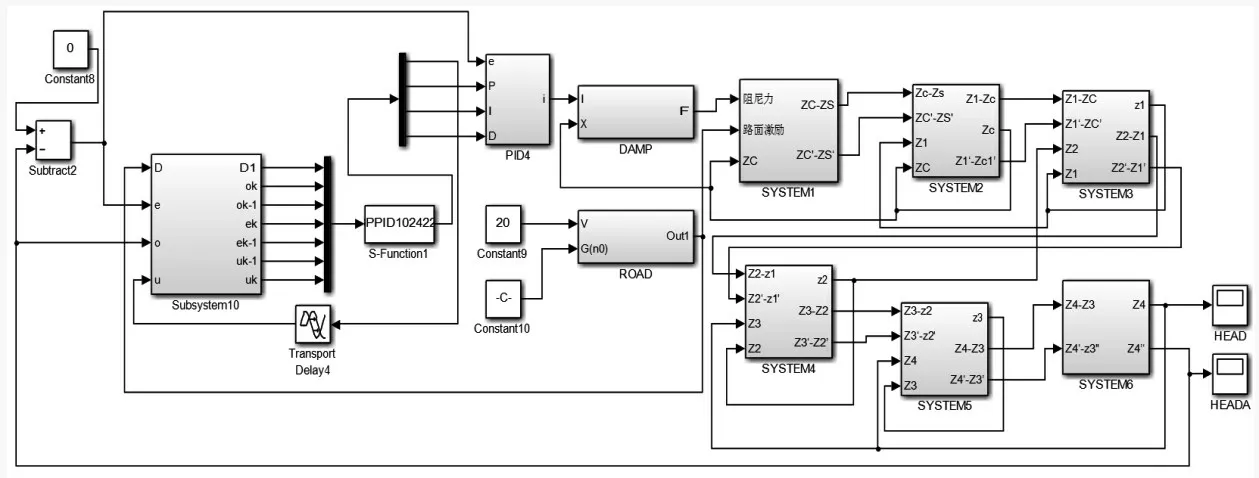
图10 座椅悬架系统框图Fig.10 Seat Suspension System Block Diagram

通过输出值与误差值等参数实时调整PID控制器使系统能够适应当前的干扰并消除误差达到最优的控制效果[15]。

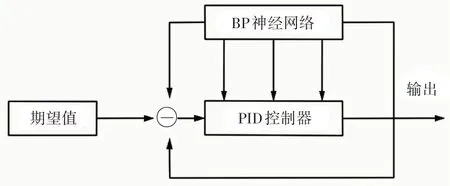
图9 BP神经网络整合PID结构框图Fig.9 BP Neural Network Integrated PID Structure Block Diagram

在MATLAB/Simulink 仿真界面中搭建仿真模型。并利用Simulink 中的S-function 模块对BP 神经网络进行编程整合PID参数，以系统不同时刻输出、控制律、误差信号作为系统的状态变量，利用随机数选取权值初值，以期望值、误差以及实际值作为神经网络的输入层的输入，以PID控制策略三个参数（KP、KI、KD）作为输出。通过偏差信号不断对权值进行实时修正，选择对数S型传递函数为BP神经网络的激励函数，并利用子系统封装技术将各个模块进行封装，最终得到其仿真系统结构，如图10所示。

5 仿真结果分析

头部是人体最重要的部位之一，通过颈椎与人体相连，许多重要器官均在头部，因此头部对振动也最为敏感。

晕车现象大部分是因为头部所受到的振动频率达到了人体所能承受的频率极限，因此，头部所受的振动位移与加速度是反映人乘坐的舒适度的重要标准，尤其是驾驶员在驾驶过程中，车辆行进时产生的振动会严重影响乘坐的舒适度以及车辆行驶的安全性，长期处于高强度的振动甚至会引发一些颈椎疾病，因此本文选取驾驶员头部的加速度和位移信号作为研究对象，分析随着时间的延长驾驶员头部的加速度及位移变化曲线，如图11、图12所示。

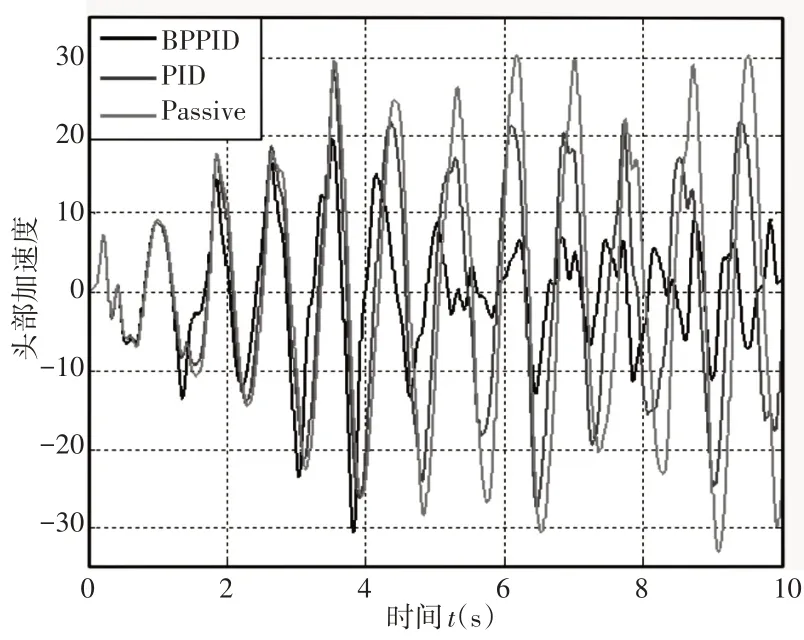
图11 头部加速度曲线Fig.11 Curve of Head Acceleration

图12 头部位移曲线Fig.12 Curve of Head Displacement

通过仿真曲线可以看出，被动悬架的减振效果＜PID控制悬架效果＜BP-PID 组合控制悬架效果，并随着时间的延长，应用BP-PID 控制策略的座椅悬架头部加速度和头部位移会越来越小，因此比较适合于长途行驶的车辆中。

6 结论

运用BP神经网络与PID 结合的控制策略对车辆磁流变半主动座椅悬架进行减振控制，能够减小车辆在行进时所产生的振动。

通过建立人-座椅-车辆七自由度模型，将磁流变阻尼器应用于汽车座椅悬架，并对比被动座椅悬架，PID 控制座椅悬架，BP-PID组合控制座椅悬架三者的驾驶员头部的加速度和位移响应对该理论进行了实验验证。

实验表明，采用BP神经网络在线整合PID参数可以使得座椅悬架具有良好的减振效果，并随着时间的延长，BP-PID组合控制的座椅悬架系统具有更好的减振性能。