矿物界面破碎特征分析与预测

蔡改贫，余 成，郝书灏，宣律伟

(江西理工大学 a. 机电工程学院; b. 江西省矿冶机电工程技术研究中心，江西 赣州 341000)

矿石是由各种金属元素矿物和非金属元素矿物经过复杂地质作用形成的集合体，具有一定的结构特征，其内部存在不同尺度的微结构面，如矿物的节理、晶粒边界、微裂隙等，这些缺陷的存在和岩石本身是一个复杂集合体，其组成成分包含各种矿物颗粒、微小颗粒、层状结构、胶结物等，使岩石在变形和破坏过程中与连续介质存在差异，表现出各向异性的特征[1]。

20世纪80年代，诸多学者发现在岩石力学领域中存在普遍的分形现象，在岩石的缺陷分布、断层等结构特征和强度、能耗等力学特征中均有所表现。Li等[2]通过分析颗粒的分布和接触状态，并利用分形维数描述颗粒分级的复杂性，提出合理设计分形间隔的概念，确定了最佳密实度的分形维数。丁自伟等[3]采用分形维数理论与数值计算相结合的方法，构建颗粒孔隙分布特征与力学强度的相关关系，实现对岩石强度特性的快速评价与估测。宋宇等[4]通过重构砂岩巴西劈裂试验后节理表面形貌模型，引入随机分形数字高程模型生成方法，迭代生成一系列不同形貌特征的分形粗糙表面数字高程模型。Lin等[5]通过分析典型碎屑断面晶体轮廓的分形维数，发现劈裂破坏的晶体轮廓分形维数相对较小，剪切破坏的晶体轮廓分形维数相对较小。Xie等[6]通过建立三维打印断裂模型，研究了分形维数对流体流动特性的影响，发现不同方向断面的裂缝线的分形维数在1.01～1.03之间。龚爽等[7]通过对半圆形煤样进行冲击条件下的断裂特性测试，结合图像处理技术和分形维数计算方法，分析了层理和加载速率对煤中动态裂纹扩展分形特征的影响。杨阳等[8]通过对岩石进行霍普金森压杆(SHPB)进行动态冲击试验，并结合分形理论，研究了岩石在低温和冲击载荷作用下往往胶结物处优先产生破坏。刘享华等[9]通过对裂隙砂岩进行单轴压缩实验，并基于分形理论定量描述了砂岩破坏后碎屑尺度分布的分形特征。刘海峰等[10]通过开展红砂岩-混凝土界面剪切对比试验,揭示2种不同沉积作用类型的岩石与混凝土黏结面产生剪切强度差异的根本原因。

反向传播(back propagation, BP)神经网络是一种可进行学习并保存输入输出映射关系的多层前馈网络，通过学习和训练输入样本，可得到数据中的隐藏规律，并利用学习到的规律来对未来数据进行预测。Afaq等[11]基于钢筋混凝土试件(即梁)相关的关键设计参数的承载能力变化的信息，建立了能够快速、准确地预测钢筋混凝土结构承载力的人工神经网络模型。Li等[12]利用BP神经网络对储层重构数据进行非线性拟合，提出了一种预测页岩气藏产量的方法，得到页岩气井产量预测模型。董珍一等[13]提取超声仿真信号的时域、频域及小波分解时频域衰减系数，探究其与涂层孔隙分布均匀性的绝对斜率k与均匀性长度LH之间的相关性，并作为反向传播神经网络(back propagation neural netwok，BPNN)的输入对斜率k与均匀性长度LH进行预测。邓念东等[14]构建了BP神经网络模型和主成分分析-反向传播(principal component analysis-back propagation，PCA-BP)神经网络模型，对风积砂充填体进行强度预测，并选取影响充填体强度的黄土含量、风积砂含量、水泥含量、粉煤灰含量、浓度及固化时间6个参数开展测试。Xi等[15]通过建立人工神经网络预测模型，预测并分析了混凝土界面过渡带的细观尺度断裂特性。

综上可知，为研究岩石的破碎机理，提高岩石的破碎效率提供了一定的理论和依据，但在利用岩石可见分形特征预测不可见破碎特征的研究甚少。本文中基于矿石的岩相分析，利用分形理论研究组分矿物界面几何特征，利用原位加载实验获取组分矿物界面力学特征，并基于BP神经网络训练可见的几何特征，达到预测界面力学特征的目的，为研究矿石破碎，提高有用矿物快速、高效解离破碎提供新思路。

1 盒子维法原理

矿物界面几何分析主要指对组分界面的粗糙起伏特征进行分析，但该特征用简单的数学关系难以准确描述。分形几何是一种能够在研究自然界中看似无序的不规则复杂结构做出定量描述的新方法，其在轮廓粗糙度的定量描述中得到广泛应用。

设集合F⊂Rn，令Nε(F)表示用边长为ε的N维几何体(盒子)填充集合F所需盒子的数目，则F的盒子维DF定义为

(1)

由于盒子维原理简单、计算方便，在分形维数中被广泛应用。由式(1)可知，当ε趋于0，即测量尺度极小时，即可迅速地体现集合的不规则性。

由盒子维的定义可知，维数的大小只与不同尺度测量得到的盒子数目有关，因此，盒子维能够反映不同尺度下集合的几何情况。

将目标轮廓的灰度值作为高度，即可使灰度图成为高低起伏的三维分形曲面，令N(F)表示覆盖目标轮廓区域所需边长r为的立方体最少个数。待测轮廓的分形维数D主要由式(2)决定，具体计算过程为

N(r)rD=C,

(2)

式中C为常数。

对上式两边同时取对数有

lg[N(r)]=-Dlgr+lgC。

(3)

设待测图像区域的面积为A，大小为该区域所包含像素点的多少，待测图像区域的单位面积为目标轮廓区域所需边长的平方，即r×r；且r的尺度为可变值(r=1,2,3,…)，令

(4)

式中：Ii(i=1,2,3,4)表示单位区域4个顶点灰度值大小；int表示取整；n(r)表示填充单位面积内灰度所要的r3个数。

计算A内每个单位面积所覆盖的立方体个数，记为n1(r),n2(r),…, 求其均值，用E(n(r))表示，则有

(5)

现在改变r的大小，求出相应的N(r)，再用线性回归，即将不同边长的r与N(r)代入式(3)，求出lgN(r)相对于lgr的曲线斜率，即可得到该图像区域的分数维。

2 界面特征预测分析

2.1 矿石试样制备

以某黑钨矿石(主要有用矿物为金属钨，脉石矿物为石英和硅质岩)为研究对象，采用角磨机(安装切割片)对矿石试样进行分割处理，将不规则形状矿石制成厚度约1 cm的片状矿石试样，其中白色组分为石英矿物、灰黑色组分为硅质岩矿物、亮白色组分为钨矿物，其处理前、后矿石试样如图1所示。

初步切割的片状矿石试样的切割截面受设备、夹具和人工操作等因素影响，产生较大的加工误差导致片状矿石切割截面不平整，因此采用0.12 mm纸和0.038 mm砂纸分别对片状矿石切割截面进行粗磨和细磨处理，使切割截面能在USB数码显微镜下显示图像清晰、组分矿物及其界面易区分的矿石岩相。

2.2 界面几何特征分析

通过对黑钨矿石进行切片处理，获取黑钨矿物内部截面，利用USB500X数码显微镜(上海韧跃电子科技有限公司)对矿石切割截面进行放大观察，并对金属钨颗粒分布区域进行不同率岩相采集。

图2为黑钨矿石切割截面中采集的钨颗粒岩相，由于所选黑钨矿石为上面石英、下面硅质岩的结构且受杂质、焦距调节的影响，导致石英矿物在显微镜下出现明显的颜色差异。分析岩相可知，钨颗粒形状各异，颗粒边界形状从圆形、长方形等规则曲线，到复杂、随意等不规则曲线均有涉及，且钨颗粒尺寸大小差异较大。

(a)处理前(b)处理后图1 黑钨矿样处理前、后对比Fig.1 Comparisonchartbeforeandaftermineralsampleprocessing

利用图像二值分割方法对图2所示钨颗粒岩相进行处理，得到所需的石英-钨界面轮廓曲线，并在此基础上，利用盒子维法计算石英-钨界面的分形维值，计算结果如表1所示。

表1 不同条件下石英-钨界面分形维值

分析表1数据可知，石英-钨界面最小分形维值为1.855 1、最大分形维值为1.936 8，其分形维值的大小可有效解释界面的粗糙起伏程度。所求的分形维值范围为1.855 1～1.936 8，其波动范围较广，这是由颗粒形状多种多样、边界复杂多变所致。

图3为不同倍率下石英-钨界面分形维值折线图。分析该图可知，石英-钨界面分形维值在第2和3处产生较大波动，这说明石英-钨界面在较小尺度下时的粗糙起伏程度较大。对所有分形维值进行整体分析可知，除去第2组后，剩下各组的分形维值上下峰值之差仅为0.131，这说明在黑钨矿石中大部分石英-钨界面的轮廓粗糙起伏程度在较小尺度下是近似的，但仍有少数石英-钨界面的轮廓粗糙起伏程度小于平均值，即石英-钨边界几何特征相比石英-硅质岩界面更为复杂多变。

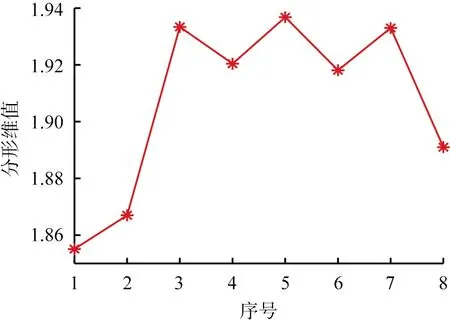
图3 不同倍率下石英-硅质岩界面分数维值折线图

利用数码显微镜在矿石切割截面分别采集不同截面、不同位置和不同倍率条件下的石英-硅质岩界面岩相。图4为不同倍率条件下的石英-硅质岩界面岩相，利用图像二值分割方法对所选岩相进行处理，得到所需的石英-硅质岩界面轮廓曲线。

(a)截面1处(b)截面2处(c)截面3处(d)截面4处(e)截面5处(f)截面6处(g)截面7处(h)截面8处图4 不同倍率下石英-硅质岩界面岩相Fig.4 Lithofaciesatquartz-siliceousinterfaceatdifferentmagnifications

在此基础上，利用盒子维法计算石英-硅质岩界面的分形维值计算，结果如表2所示。分析表中数据可知，石英-硅质岩界面最小分形维值为1.163 3、最大分形维值为1.371，其分形维值的大小可有效解释界面的粗糙起伏程度。所求的分形维值范围为1.163 3～1.37 1，也与实际矿石中石英-硅质岩界面存在一定的粗糙起伏特征相印证。

表2 不同倍率下石英-硅质岩界面分形维值

图5为所求的不同条件下石英-硅质岩界面分形维值分布图。分析该图可知，石英-硅质岩界面分形维值在第6和7处产生较大波动，说明石英-硅质岩界面在较小尺度下的粗糙起伏程度差异较大。对所有分形维值进行整体分析，可知其上、下峰值之差仅为0.231 7，说明在黑钨矿石中普遍存在的石英-硅质岩界面的轮廓粗糙起伏程度在较小尺度下是近似的，即石英-硅质岩边界几何特征可近似用同一粗糙度描述。

图5 不同倍率下石英-硅质岩界面分数维值分布图

2.3 界面力学特征分析

矿物界面力学特征通过对界面区域进行原位加载实验得到，原位加载实验通过无锡欧凯电子研制的万能材料试验机实现，如图6所示。

(a)整体视图(b)工作台放大视图图6 原位加载实验装置Fig.6 In-situloadingexperimentaldevice

为成功实现对组分矿物界面的原位加载实验，考虑到矿石各组分矿物中钨颗粒尺寸最小，结合钨颗粒长度、面积等尺寸参数和万能材料试验机结构参数，自制原位加载实验所需压头(直径为2 mm)，如图7所示。

图7 自制原位加载压头

黑钨矿石试件中石英矿物、硅质岩矿物和钨矿物3种组分矿物分别以聚集体形式存在，且各组分矿物相互粘结形成矿石整体，而不同组分矿物在粘结过程中形成石英-硅质岩界面和石英-钨界面，分别对2种矿物界面进行原位加载实验，并通过控制液压速率，获得不同加载速率下各矿物界面最小破碎应力实验数据。

表3为黑钨矿石组分矿物界面原位加载实验数据，其中实验1—4的加载速率为0.01 kN/s、实验5—8的加载速率为0.005 kN/s。分析表中数据可知，2种加载速率下组分矿物界面的抗压强度比较接近，其中石英-硅质岩界面最小破碎应力范围为1.178 5～1.482 6 GPa，石英-钨界面最小破碎应力范围为1.335 5～1.542 03 GPa。

表3 组分矿物界面最小破碎应力

表4为不同加载速率下，黑钨矿石组分矿物界面在原位加载实验中产生的最大破碎应变数据，其中实验1—4的加载速率为0.01 kN/s、实验5—8的加载速率为0.005 kN/s。分析表中数据可知，组分矿物界面产生的应变不受加载速率影响，其中石英-硅质岩与石英-钨界面界面产生的最大应变范围均为0.000 157～0.000 169。

表4 组分矿物界面最大破碎应变

组分矿物界面的最小破碎应力虽然反映了矿物界面破坏的临界值，但矿物界面在加载过程中内部的力学性能变化却无法通过最小破碎应力表现。应力-应变曲线形状能够反映矿物界面在外力作用下产生的各种变形过程，如脆性、塑性、屈服、断裂等。传统的应力-应变曲线分析方法是将曲线按照峰值应力的百分比分为弹性阶段、屈服阶段、强化阶段和局部变形阶段，其中弹性阶段与屈服阶段、屈服阶段与强化阶段的临界应力分别为峰值应力的25%、80%。

图8为2种加载速率下石英-硅质岩界面原位加载实验得到的应力-应变曲线。对比分析可得，在较快的加载速率作用下，曲线更为整齐光滑。分析图8(a)可知，4条曲线在弹性阶段和屈服阶段曲线趋势比较相似，在此过程中，加载区域先产生弹性应变，再产生塑性应变，使加载区域内部孔隙闭合。在局部变形阶段，曲线长度较短，即在较短时间内完成所选界面内部裂纹扩展、聚集，并达到宏观破坏的效果，这说明粘结界面在较少的微观裂纹聚集下即可发生宏观破坏。

分析图8(b)可知，在弹性阶段，4条曲线形状或凹或凸，即加载区域在载荷作用下，产生较小的弹性应变后立即产生塑性应变，直至屈服阶段，加载区域在较大应力作用后，内部微观缺陷被闭合。在强化阶段，几条曲线的应力增长缓慢，且应力时有下降，但应变快速增大，此时，内部不断产生微裂纹，并不断聚集直至形成宏观破坏。

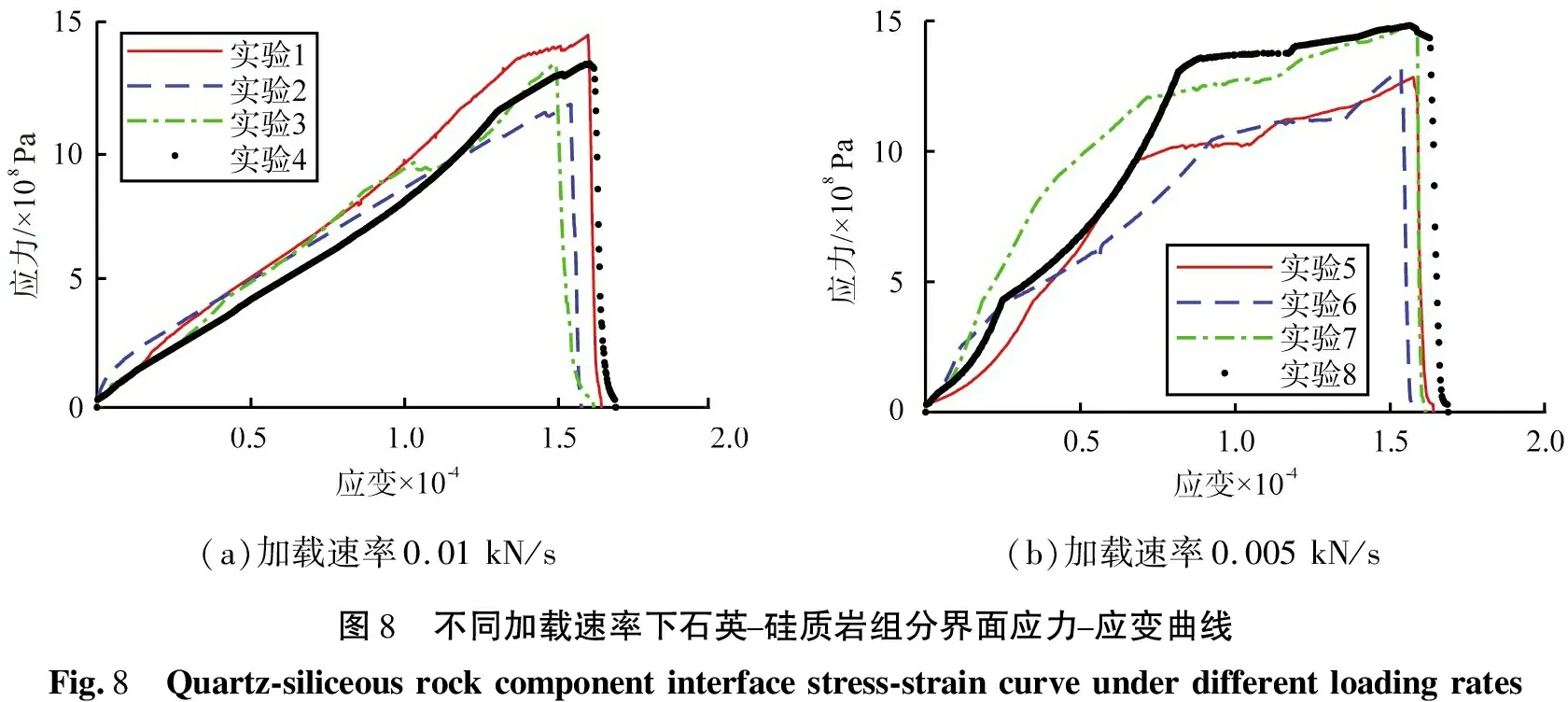
(a)加载速率0.01kN/s(b)加载速率0.005kN/s图8 不同加载速率下石英-硅质岩组分界面应力-应变曲线Fig.8 Quartz-siliceousrockcomponentinterfacestress-straincurveunderdifferentloadingrates

图9为2种加载速率下石英-钨界面原位加载实验得到的应力-应变曲线，对比分析可得，在较快的加载速率作用下，曲线更为整齐光滑。分析图9(a)可知，弹性阶段曲线形状近似直线、屈服阶段曲线形状具有凹度，表明弹性阶段应力可恢复、屈服阶段降低界面处孔隙率。但弹性阶段和屈服阶段应力、应变区间不同，表明不同区域的石英-钨界面的结构性能和力学性能也存在差异，这是由钨颗粒形状、尺寸的差异造成。局部变形阶段曲线产生明显的波动，且在相差较小的应力范围内产生较大的应变，表明石英-钨界面的破坏需要较多的微裂纹聚集，并在峰值应力下产生宏观破坏。

分析图9(b)可知，在弹性阶段和屈服阶段，实验1和3曲线趋势相似、实验2和4曲线趋势相似，这是由于颗粒形状、尺寸差异导致界面力学性质差异，但4条曲线在强化阶段曲线趋势相似，这是由于加载速率较低时，经过弹性阶段和屈服阶段，较小的应力增长可产生较大的应变，并形成足够的微裂纹，最终聚集形成宏观破坏。

综合分析2种加载速率下黑钨矿石组分矿物界面原位加载实验得到的应力-应变曲线可知，加载速率对屈服阶段和强化阶段具有较大的影响，但加载速率较大时，强化阶段应力会突然降低发生抖动，当加载速率较小时，强化阶段应力则是先趋于相对平稳状态后产生降低。

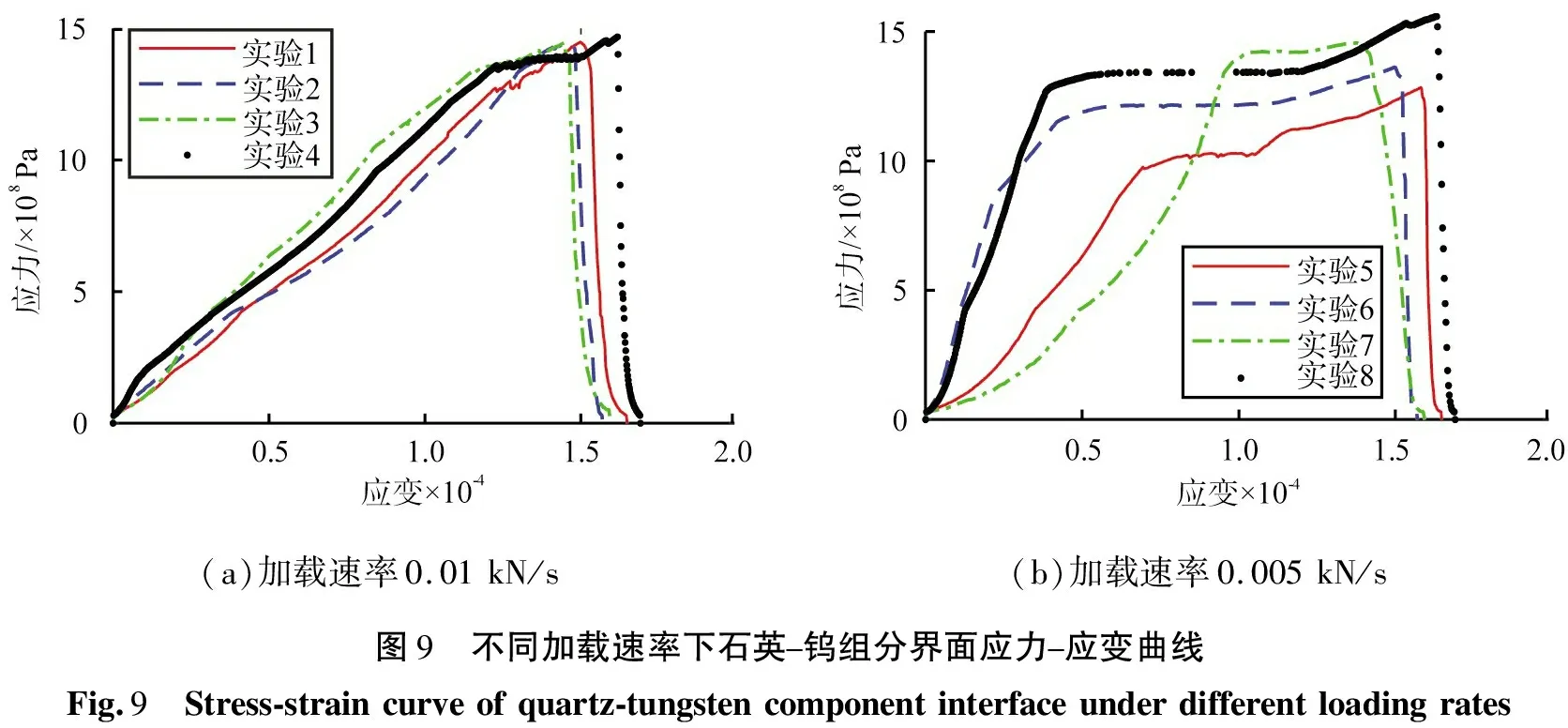
(a)加载速率0.01kN/s(b)加载速率0.005kN/s图9 不同加载速率下石英-钨组分界面应力-应变曲线Fig.9 Stress-straincurveofquartz-tungstencomponentinterfaceunderdifferentloadingrates

2.4 界面特征预测

用于界面特征预测的算法主要有灰度预测、深度学习、BP神经网络等。考虑到BP神经网络具有高度的自学习与自适应能力，且在处理非线性问题具有很大的优势，尤其在对系统无确切的数学模型下，依然可以模拟任何非线性函数关系，因而BP神经网络在预测领域得到广泛应用[16]。基于此，并结合矿物界面几何与力学特征，可以通过建立BP神经网络模型来对矿物界面特征进行预测。

本文中通过利用MATLAB软件，创建BP神经网络预测的程序，并以黑钨矿石组分矿物界面可观察的分形维值作为网络输入样本数据，组分矿物界面破碎应力作为网络输出样本数据[17-18]。

2.4.1 数据预处理

由于实验采集的样本数据存在量纲差异，为提高网络的训练能力，并获得更加精确的预测数据，因此，需对原始输入与输出样本数据进行预处理，在MATLAB软件中采用内置的数据预处理premnmx函数对样本数据进行归一化处理，并生成函数

[pn, minp, maxp,tn, mint, maxt]=premnmx(p,t)，

式中：p表示输入原始样本数据；t表示输出原始样本数据；pn和tn分别表示原始输入样本数据p与输出样本数据t归一化处理后的样本数据集，且归一化处理后数据范围为0～1之间；maxp与minp分别表示p矩阵每一行的最大值与最小值；maxt与mint分别表示t矩阵每一行的最大值与最小值。

2.4.2 网络模型建立

在进行模型生成时，选择训练函数traingdx对网络进行训练，其优点是计算速率快，误差小。根据BP神经网络的结构设计，其隐藏层和输出层的激活函数分别采用系统默认的tansig函数与purelin函数，通过测试多个网络后，隐藏层最佳神经元数为7，生成网络的程序表达式为

net=newff(dx,[1,7,1],{‘tansig’,‘tansig’,‘purelin’},‘traingdx’)，

式中：net为生成的BP神经网络；dx为输入元素的范围；newff为初始化函数，其在生成BP网络时已重新定义网络各层权值和阈值的初始化函数。

2.4.3 模型仿真

经过多次程序测试，得到网络训练的主要参数为

net.trainParam.show=1 000,

net.trainParam.Lr=0.05,

net.trainParam.epochs=500 00,

net.trainParam.goal=0.000 65。

利用训练函数对网络进行训练，其程序表达式为

net=train(net,pn,tn),

式中：pn为归一化处理后的输入样本数据矩阵，即黑钨矿石组分矿物界面可观察的分形维值；tn为归一化处理后输出样本数据矩阵，即组分矿物界面破碎应力。

把已训练好的数据通过调用sim函数进行仿真，其表达式为

an=sim(net,pn),

a=postmnm(an,mint,maxt)，

式中：pn为归一化处理后输入数据；an为通过利用sim函数仿真后的数据；postmnm为反归一化处理函数；a为仿真训练后输出的最终数据，将其与真实试验值进行对比分析，即可得到此次训练的效果。

2.4.4 预测结果分析

利用MATLAB软件对网络进行训练，并通过采用线性回归的方法对预测结果和训练结果作相关性评价，结果如图10、11所示。根据图10曲线的变化规律可得，训练的误差曲线迅速下降后趋于平稳。由图11可知，网络输出回归线的相关系数R=0.964 5，相关程度非常高，因此，网络具备良好的预测性能。

通过对训练结果与实际结果对比分析，可更加有效地实现矿物界面几何特征与力学特征相结合，对不同组分矿物界面破碎力学特征进行预测。

图12为利用BP神经网络结合黑钨矿石组分矿物界面分形维值对矿物界面破碎应力的映射规律预测图，图中符号“o”代表应力预测值、“+”代表应力实际值，分析图12(a)可知，在预测前期，数据之间存在一定差距，但随着样本数据的增多，预测值与实际值之间的差距逐渐减小。图12(b)为应力的预测值与实际值之间的误差分布图。分析该图可知，预测误差范围为0.011%～4.14%，且总体误差均低于2%，因此，BP神经网络具有较高的预测精度，可有效的利用表面矿物界面几何特征预测界面破碎应力。

图10 误差均方曲线Fig.10 Errormeansquarecurve图11 网络输出回归分析线Fig.11 Networkoutputregressionanalysisline

(a)应力预测曲线(b)预测误差图12 矿物界面几何特征对应力预测及其误差图Fig.12 Effectofgeometriccharacteristicsofmineralinterfaceonstresspredictionanditserrormap

3 结论

1)所研究的黑钨矿物主要为石英-硅质岩界面和石英-钨界面，且石英-钨界面分形维值大于石英-硅质岩界面的，石英-硅质岩界面分形维值范围为1.163 3～1.371，石英-钨界面分形维值范围为1.855 1～1.936 8，与实际矿石中矿物界面存在一定的粗糙起伏特征相印证。

2)对钨矿石试样进行加载速率分别为0.005、0.01 KN/s的原位加载实验发现，石英-硅质岩界面最小破碎应力范围为1.178 5～1.482 6 Pa，石英-钨界面最小破碎应力范围为1.335 5～1.542 03 GPa。加载速率对矿物界面及内部形变具有较大的影响，且加载速率较大时，强化阶段时应力易突然降低并不断波动。

3)利用BP神经网络可实现矿物界面可见的几何特征对不可见的力学特征的有效预测，且随着样本数据的增大，预测精度越来越高，且在预测前期，预测误差最大仅为4.14%，而在预测后期，预测误差最小仅为0.011%。通过BP神经网络训练矿物界面可见的几何特征，预测矿物界面力学特征，为矿石破碎及有用矿物高效解离提供理论基础。