IPSO-EKF融合算法的SOC估算研究

叶丽华，王海钰，施烨璠，薛定邦，李 杰，施爱平

(1.江苏大学 汽车与交通工程学院，江苏 镇江 212013；2.纽约州立大学 电子与计算机工程学院，纽约 13903；3.江苏大学 农业工程学院，江苏 镇江 212013)

锂离子电池因其绵长的循环寿命和超高的能量密度被广泛应用于电动汽车，为了保证电动汽车安全可靠且高效地运行，一个精密的电池管理系统(BMS)至关重要，而作为其核心技术的SOC估算，近年来一直是研究的热点问题。动力电池的建模作为SOC估算的基础，其重要性不言而喻，等效电路模型通过一系列的电阻、电容及恒压源等电路元器件组成电路网络来模拟其外特性，如PNGV、Rint及Thevenin模型等[1]。

卡尔曼滤波(KF)正是一种基于模型的SOC估算方法，它通过构建状态空间方程，将SOC视为状态变量进行迭代计算来提高估算精度[2-4]。随着研究的深入，卡尔曼滤波算法发展出了不同的种类：扩展卡尔曼滤波算法(EKF)通过将经典卡尔曼滤波在一阶泰勒公式展开略去高阶项得到，它是KF的非线性化延伸，缺点在于面对高度非线性化的系统时，SOC估算值不收敛[5-6]；无迹卡尔曼滤波(UKF)利用无迹变换(UT)，通过非线性模型选择并传播一组Sigma点，从而提供状态向量的均值和协方差的近似值，缺点在于鲁棒性稍差且UT变化比较复杂[7-9]；分数阶卡尔曼(FOKF)基于分数阶微积分而提出，部分程度上解决了整数阶模型无法准确描述锂离子电池固相锂离子扩散和双层效应的问题，但问题在于其很大程度上依赖于底层模型的准确度[10-12]；容积卡尔曼滤波(CKF)是在3阶球面径向体积准则的基础上，利用一组体积点，逼近附带高斯噪声的非线性系统的状态均值和协方差，其不足之处在于底层模型往往过于简单，无法精确模拟电压的回弹特性[13-14]。在等效电路模型足够精确的情况下，任意一种KF算法均可实现较高的SOC估算精度，但问题在于除EKF外，其余算法过于复杂且计算量巨大，对于电动汽车BMS的硬件配置提出了更高的要求。

扩展卡尔曼滤波算法能得到状态变量的最优估计，不仅适用于动态系统状态估计，还可用于动态系统时变参数的估计，其不足之处在于辨识效果严重依赖噪声统计特性，而在单独使用EKF进行SOC估算时，其系统噪声协方差矩阵以及观测噪声协方差矩阵多为随机给出，因此，仅依靠EKF，系统噪声和测量噪声的统计特性很难获得最优解。粒子群优化算法(PSO)是一种生物进化算法，种群中的每个粒子都代表问题的一个潜在解，对应一个由适应度函数决定的适应度值。每个粒子都具有位置和速度2个属性，离子的位置即当前的值，粒子的速度决定了粒子移动的方向和距离，速度随自身及其他粒子的移动经验进行动态调整，实现个体在可解空间中的寻优[15-17]。PSO全局寻优的特性非常契合EKF中对于噪声协方差矩阵中元素的寻优，但PSO算法也存在遍历性差和容易陷入局部极小的缺陷。

在此基础上，本文提出了一种改进粒子群算法(IPSO)耦合EKF算法的融合算法，通过对粒子群寻优算法(PSO)的改进[18]，对EKF的噪声协方差矩阵进行种群寻优，从而提高SOC的估算精度。本文的创新性有以下2点：

1)以往的卡尔曼滤波算法及其变体算法出于简便性及鲁棒性的考虑，等效电路模型往往比较简陋，多为1阶或者2阶RC电路，本文采用了一种新型的3阶等效电路模型作为底层电路模型，结合离线辨识的方法辨识模型参数，在保证模型不至于太过复杂的同时，保证了模型的精确性。

2)以往的基于等效电路模型的SOC估算方法，为了保证算法的精确性，融合了很多繁复的数学思维和推导变换过程，使得估算过程过于庞杂且耗时较长，与此同时，又忽略了对于噪声的优化。本文提出了一种将EKF方法与IPSO算法相结合的融合算法，在EKF迭代过程中，利用IPSO算法对系统噪声和观测噪声进行寻优，提高SOC的估算精度。

1 电池特性及试验平台

以18650磷酸铁锂动力电池为对象展开研究，其单体电池主要性能参数如表1所示。

表1 单体电池性能参数

本文中所用到的电池测试设备是宁波拜特公司的NBT30V100AC4-T的电池测试系统，主要由高精度数据测试采集一体机、恒温箱和上位机组成，其主要技术参数如表2所示。

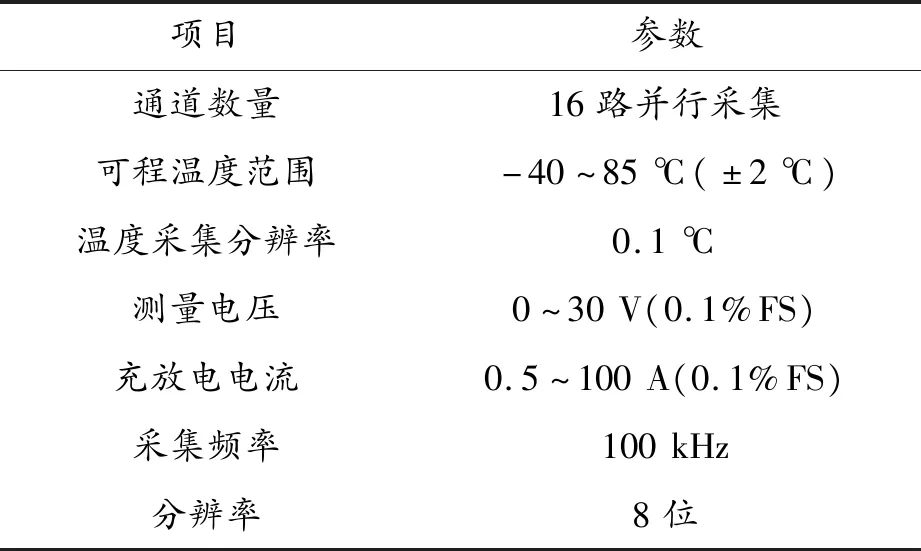
表2 NBT30V100AC4-T电池测试系统主要技术参数

电池测试平台及数据采集设备原理图如图1所示。

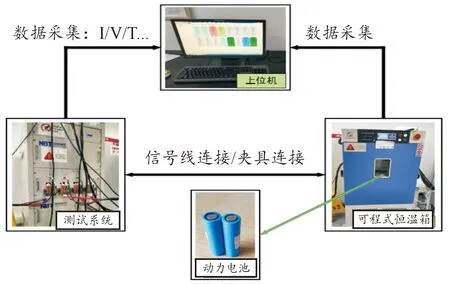
图1 电池测试平台及数据采集设备

2 等效电路模型选取及参数辨识

2.1 3阶等效电路模型的选取

等效电路模型以动力电池的伏安特性关系为基础进行建模，使用一系列电容、电阻及恒压源等电路元器件组成电路网络，描述动力电池的外特性，且复杂程度较低，具有较高的估算精度，是目前应用最广泛的电池模型。由于锂电池的外特性并不是完全一致的，基于本次所用动力电池的特性，即OCV-SOC曲线呈现出来的双平台特性，PNGV模型、Rint模型及Thevenin模型显然不能充分模拟电池电压的回弹特性及滞回特性，所以综合考虑模型精度及复杂程度的基础上，采用如下的3阶RC等效电路模型，如图2所示。

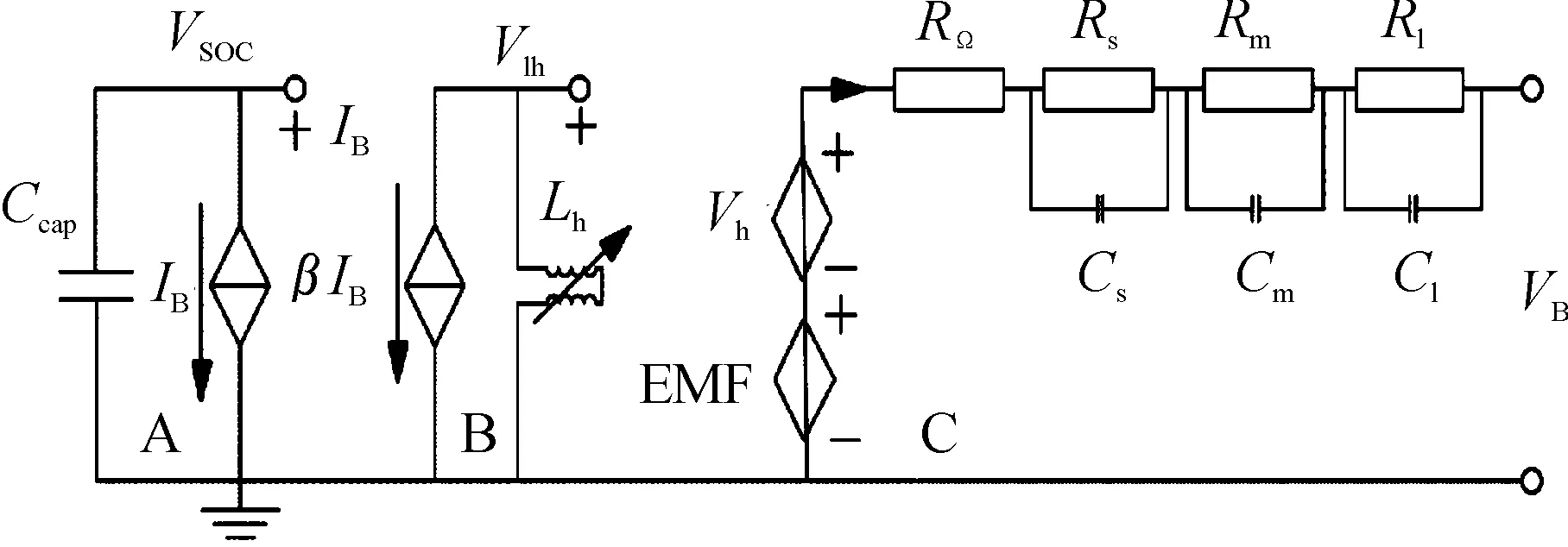
图2 3阶RC等效电路模型

图2中，Ccap代表电池的额定容量，表示EMF的电压源受电池的SOC(VSOC)控制，表示滞回电压Vh的电压源受电池的SOC(VSOC)以及VLh控制，其中，VLh控制是充电滞回还是放电滞回；RΩ代表欧姆内阻，Rs，Rm，Rl代表极化内阻，Cs，Cm，Cl代表极化电容，VB代表开路电压OCV。A、B、C支路组成受控等效电压源，模拟电池内部由于电化学极化和浓度差极化现象导致的电压滞回特性；3阶RC电路组成等效阻抗，模拟电池的回弹特性。在电流激励的作用下，上述模型的状态空间方程可表述为：

(1)

将式(1)离散化，离散时间的方程如下：

(2)

2.2 EKF滤波器设计

一般选取SOC和欧姆内阻两端的电压作为状态方程的状态变量，但是由式(2)可知，3阶RC网络两端的电压也会随电流的变化而发生状态变化，令

则式(2)可改写为如下形式：

xk=Axk-1+Bik-1

(3)

将3阶RC网络两端的电压也列为状态变量进行迭代计算，因此，EKF滤波器状态变量的选取如下：

xk=[SOC，UΩ，Us，Um，Ul]

(4)

观测变量选择动力电池的开路电压，即

yk=VB=UOCV

(5)

EKF的迭代流程可用图3表示。

图3 EKF迭代流程示意图

2.3 参数辨识

参数辨识分为在线辨识和离线辨识，在线辨识可以通过传感器实时监测的数据实现模型的在线更新，精准的捕捉系统的参数变化；而离线辨识则是通过HPPC工况，获取电池脉冲充放电瞬间的电压变化结合欧姆定律来辨识电池的阻抗参数。仅从算法的角度来说，在线辨识是以数学公示进行实时拟合，其鲁棒性更好，由于本课题采用的等效电路模型为3阶，需要辨识的阻抗数目较多，相对于Rint模型和Thevenin模型来说，模型较为复杂，在线辨识的结果并不理想。相对于在线辨识方法，离线辨识的参数更加准确和稳定。由于所用的底层电路模型为3阶等效电路模型，高阶模型在微小扰动下的辨识结果会有很大的波动，为了尽可能提高辨识精度，选择0.2C、0.4C、0.6C、0.8C、1.0C、1.2C、1.4C、1.6C、1.8C、2.0C，共10组放电倍率，对电池的阻抗参数进行离线辨识，并绘制成三维图像，结果如4所示：图4中，(a)(b)(c)为等效极化电阻，分别对应图2中Rs，Rm，Rl，(d)(e)(f)为等效极化电容，分别对应图2中Cs，Cm，Cl。每一个3维图片中，放电倍率定义为x轴，SOC定义为y轴，阻抗特性定义为z轴，上述图片反映了在3阶等效电路模型的基础上，等效阻抗在不同放电倍率和SOC值下的变化特性，从图中可以看出，当放电电流恒定时，极化内阻随SOC的降低而增大；当SOC恒定时，极化内阻随放电倍率(即放电电流)的增大而减小。极化电容的变化趋势与极化电阻相反，因为二者并联，符合电池的工作特性。

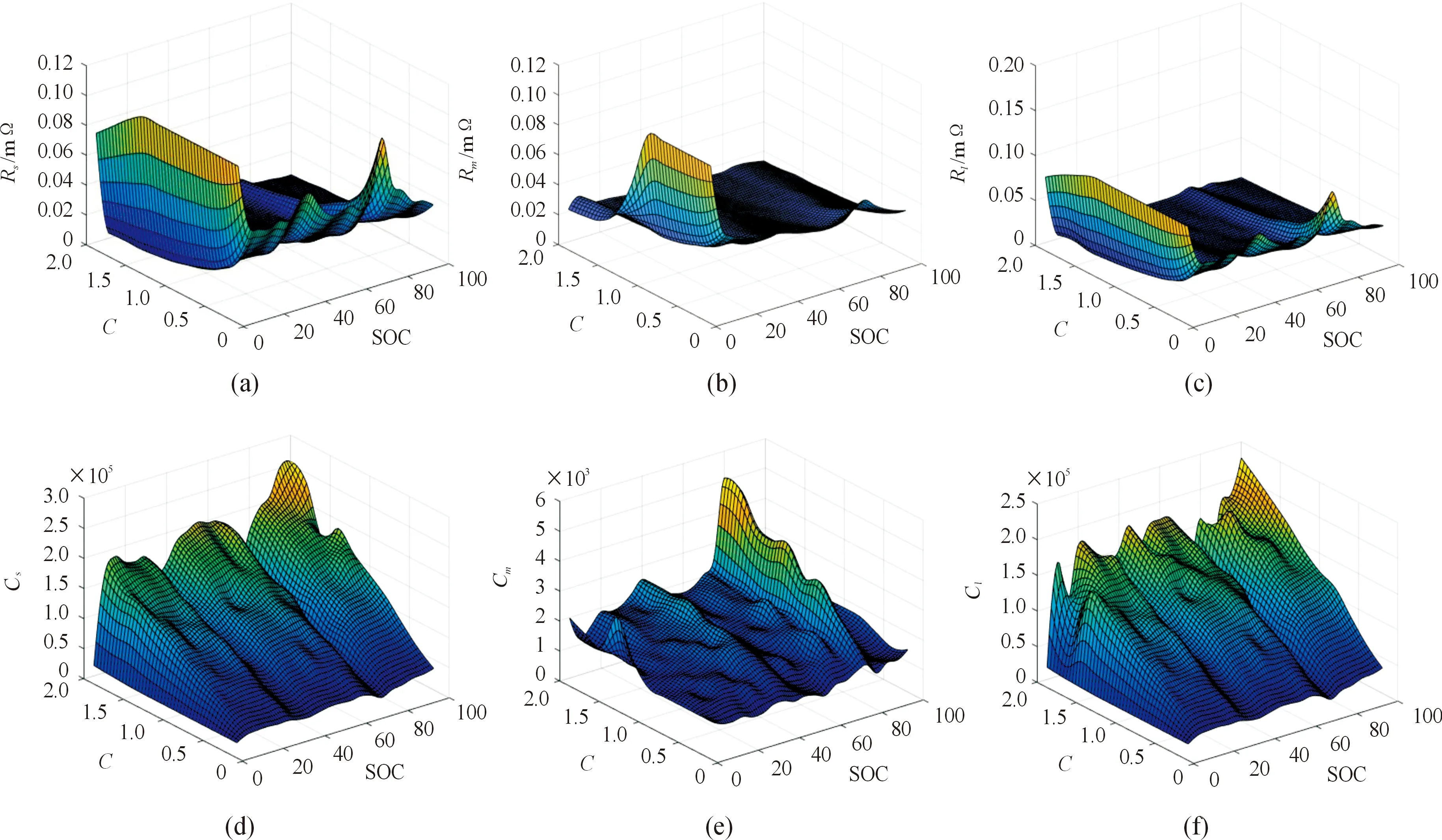
图4 等效极化电阻(a)与等效极化电容(b)的参数辨识结果

3 IPSO-EKF融合算法的原理

3.1 针对PSO算法的改进

1)针对遍历性差

采用Tent映射对粒子群位置和速度进行初始化[19]，它是分段线性一维映射的一种形式，又称帐篷映射，其数学表达式为：

xn+1=α-1-α|xn|，α∈(1，2]

(6)

Tent映射的Lyapunov指数为：

(7)

当α≤1时，λ≤0，系统处于稳定状态；当α>1时，λ>0，系统处于混沌状态；当α=2时，λmax=ln2，为中心Tent映射，其数学表达式为：

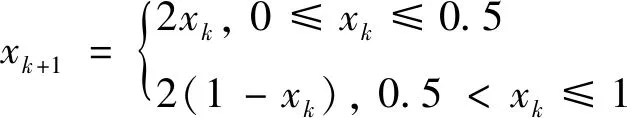
(8)

将初始化结果映射到[-1，1]区间，表达式如下：

ef，d=rf，d(2xk-1)

(9)

该式所得即为粒子群初始速度值和初始位置值。

Tent映射结构简单，具有很好的遍历均匀性，更适合大数量级数据序列的运算处理，迭代速度和遍历性要快于Logistic映射。

2)针对算法易早熟、后期易在全局最优解附近震荡

为了保持种群内部的多样性，避免算法过早在局部最优处收敛，进而导致早熟现象，引入一个带变异算子的变异控制函数[20-21]，用来控制变异的粒子数目，变异控制函数为：

y(h)=(1-(h/hmax)α)β

(10)

式中：h为当前迭代次数；hmax为最大迭代次数；α、β为控制系数。

变异算子的控制率计算公式如下：

u=m·y(h)

(11)

式中：u为变异率；m为预设变异率，设定后不变。

由式(10)(11)可以看出，通过控制α、β及变异率u的值可以控制变异函数，在算法运行前期，为了种群搜索的全面性，α、u取较大的值，迭代次数更多；在算法运行后期，为了集中寻优，快速收敛，β、u取较小的值，迭代次数更少。

进行变异操作的粒子数通过变异率确定，如下式：

M=[N·u]

(12)

式中，M是进行变异操作的粒子数。

对粒子的变异操作为：首先对种群粒子进行Tent映射，并将初始化结果按照式(9)进行赋值，之后从中选择M个粒子进行变异操作，假设第k个粒子被选中进行变异操作，如Xk=(xk1，xk2，…，xkD)，其中第j个元素发生了变异，其操作策略为：

xk，j=xk，j+rand·y(h)，rand∈(-a，a)

(13)

由式(13)可以看出，在算法前期，变异后的粒子距离变异前的粒子比较远；在算法后期，变异后的粒子距离变异前的粒子比较近。这也就意味着，算法前期搜索空间比较大，减小了过早陷入局部最优解的概率；后期搜索空间比较小，能够集中资源向全局最优解方向搜索，提高算法的收敛精度。

3)针对粒子易陷入极小值

以粒子群的位置协方差矩阵的取值作为标准，当其小于指定值时，表明粒子群陷入局部极小，重新由式(8)进行混沌映射初始化，表达式如下：

Δ=δf，d(f=1，2，…，n;d=1，2，…，D)

(14)

4)适应度函数的选取

以模型电压的模拟值与试验电压的测量值的绝对累积误差值，作为IPSO算法的适应度函数，表达式如下：

(15)

3.2 IPSO-EKF融合算法对SOC估算中的噪声优化

利用IPSO-EKF融合算法进行SOC估算中的噪声优化主要分为2个步骤，首先是在Simulink中建立基于3阶等效电路的EKF模型，其次是利用m脚本编写IPSO程序，在每个采样时刻，调用EKF模型1次，进行噪声寻优，具体的步骤如下：

在Simulink中搭建基于3阶等效电路的EKF模型，并设置好From Workspace以及To Workspace等调用接口；在Matlab中编写m脚本，并利用options=simset(′SrcWork-space′，′current′)以及sim(′EKF′，[]，options)设置好句柄；

步骤1 利用式(8)对PSO种群粒子进行Tent中心映射，并完成初始化；

步骤2 判断是否达到最大迭代次数；

步骤3 用式(15)计算粒子适应度值；

步骤4 计算各个粒子的协方差矩阵；

步骤5 利用式(14)判断种群是否陷入局部极小，判断标准为所有粒子群都满足式(14)；

步骤6 判断为是，利用式(10)对种群粒子进行变异操作，并返回步骤1；

步骤7 判断为否，更新粒子位置和速度，并按照式(9)，将粒子群最优解赋值给Simulink中EKF模型的噪声协方差矩阵Q、R；

步骤8 将Q、R带入EKF模型进行一次迭代计算，并对电流、仿真电压、测试电压以及雅可比矩阵进行采样，并计算SOC。

步骤9 输出SOC，将此时的Q、R所对应的粒子群速度和位置定义为种群历史最优，并将其值返回步骤3，继续进行迭代计算。

以上为IPSO-EKF在SOC估算中进行噪声寻优的递推步骤，其融合算法流程以及子模块局部放大图如图5所示。

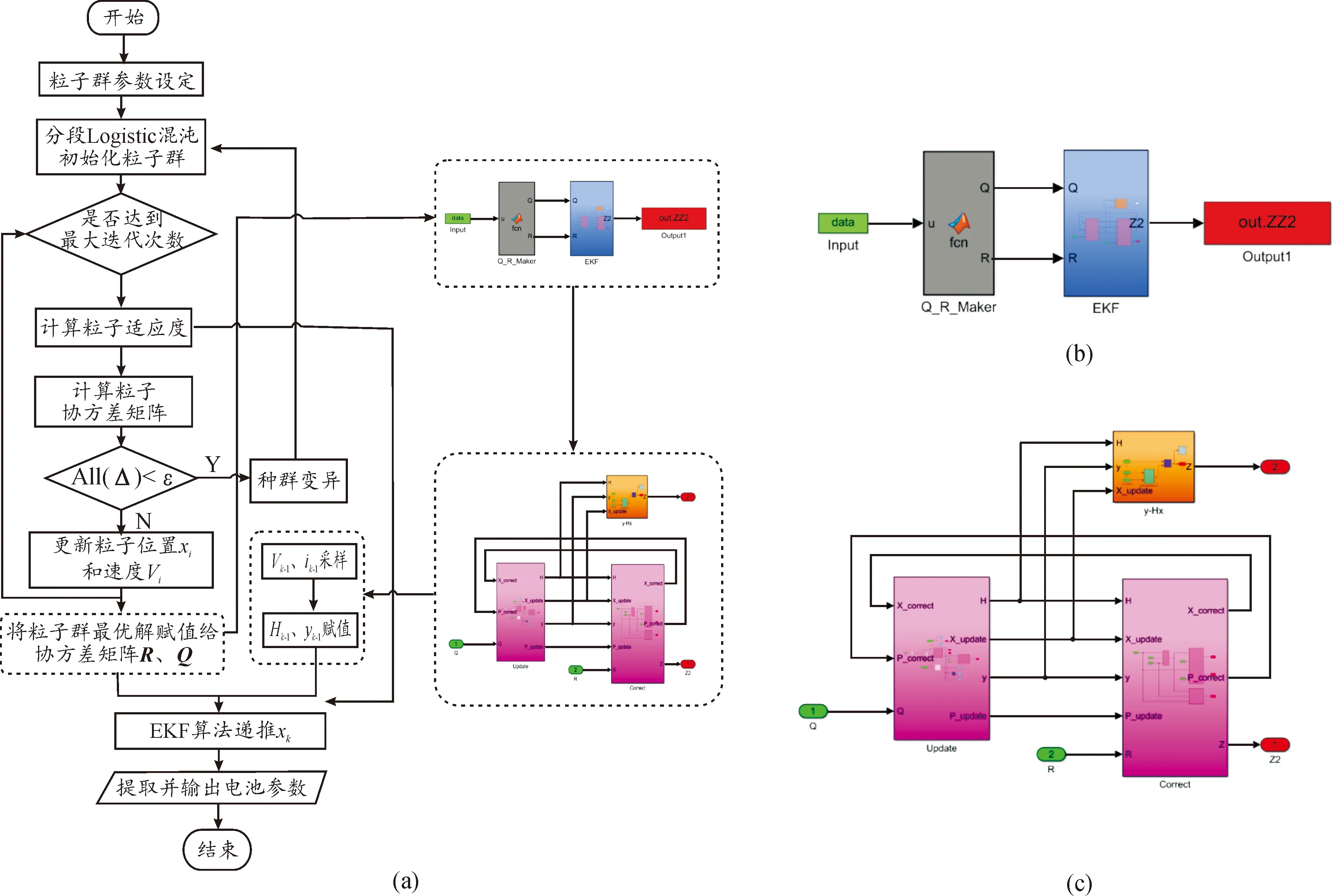
图5 IPSO-EKF融合算法流程框图以及子模块局部放大图

4 试验与算法验证

4.1 参数辨识验证

首先对3阶等效电路模型下的离线辨识结果进行验证，验证的方式为端电压验证，即在Simulink模型中输入不同动态工况的电流激励，模型会产生一个对应的仿真电压，将其与试验电压进行对比即可，IPSO-EKF算法的仿真电压定义IPSO-EKF，试验工况的真实电压以具体的试验名称定义。

如图6所示，验证工况选用DST工况、UDDS工况以及NEDC工况，其中，DST工况和UDDS工况侧重于模拟城市驾驶条件下动力电池的负载变化；而NEDC工况兼顾城市和市郊驾驶条件下动力电池的负载变化。由图6可以看出，基于3阶等效电路模型下的模型仿真电压与动态工况测试电压观测值大部分重合，误差基本在-0.02～0.06 V，说明在离线参数辨识的情况下，3阶等效电路模型可以很好地进行模型参数识别。

图6 DST、UDDS以及NEDC工况下的电压验证

4.2 基于IPSO-EKF融合算法下的SOC估算验证

分别基于DST工况、UDDS工况以及NEDC工况进行了IPSO-EKF算法验证，结果如图7所示。图7中，以实验室状态下安时积分法测得的SOC作为基准值，并定义为True SOC；EKF算法估算的SOC定义为EKF-SOC，需要注意的是，系统噪声协方差矩阵和观测噪声协方差矩阵均为仿真平台随机生成，以此作为对比；IPSO-EKF算法估算的SOC定义为IPSO-EKF-SOC，该曲线是已经经过IPSO-EKF算法优化噪声之后的SOC估算曲线。由图中可以看出，在SOC估算初期，由于EKF算法的噪声协方差矩阵为仿真平台随即给出，其SOC估算曲线没有及时收敛到True SOC，导致后期估算曲线越来越偏离真实值，并且逐渐出现发散的趋势；而IPSO-EKF-SOC由于对噪声进行寻优，曲线从放电开始，就及时收敛到了True SOC，且在后续的SOC估算过程中，一直保持在True SOC附近。此外，从误差曲线也可以看出，在仿真开始的一瞬间，IPSO-EKF-SOC立刻收敛到True SOC附近，且在整个仿真过程中，估算误差一直保持在5%以内，而EKF-SOC估算误差越来越大，且没有出现收敛的迹象。相比于EKF算法，IPSO-EKF算法具有更高的估算精度，其估算误差比较平稳，且具有良好的适应性。

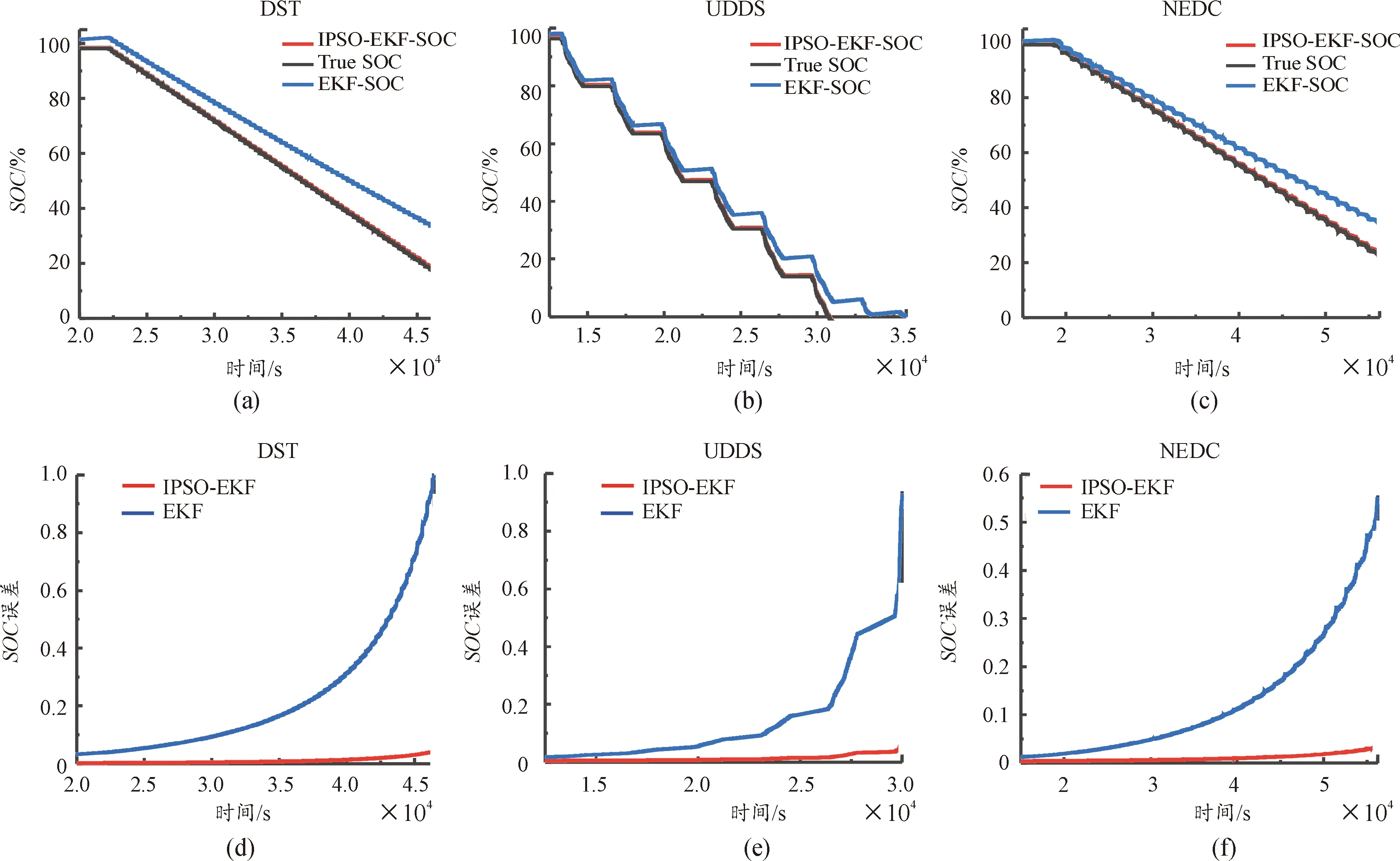
图7 DST、UDDS以及NEDC工况下的SOC估算精度比较

4.3 IPSO-EKF融合算法收敛速度

通过适应度值收敛曲线随算法迭代次数的变化来表征IPSO-EKF融合算法的收敛速度，如图8所示。由图8可知，本文提出的IPSO-EKF融合算法迭代速度较快，在前5次迭代过程中迅速收敛到全局最优位置，并且在随后的迭代过程中，最佳适应度值趋向于稳定。

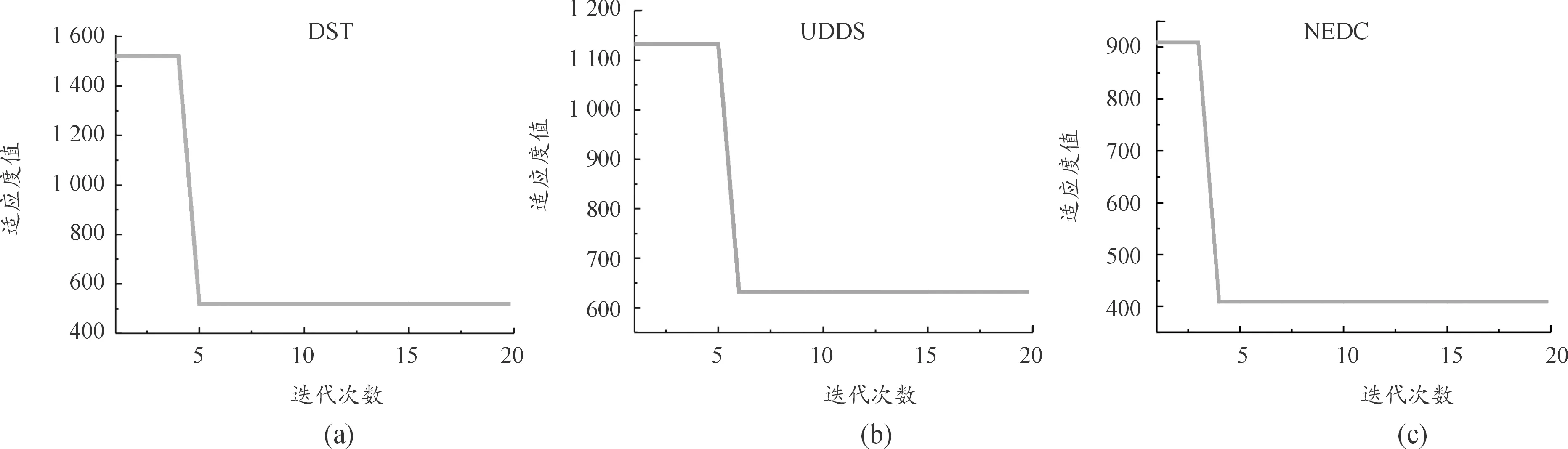
图8 DST、UDDS以及NEDC工况下的IPSO-EKF算法适应度值收敛曲线

4.4 IPSO-EKF融合算法可靠性验证

RMSE值和MAPE值通常用来作为评价一个回归模型精度的指标，其值越小，代表模型精度越高，Yang等在研究锂离子电池SOC估算问题时，提出可以用RMSE和MAPE来表征算法的精度和可靠性[9]，即将试验电压的各个采样点数据看作是离散空间中的点集，而将算法拟合的SOC曲线看作是一条回归方程。不同动态工况下的RMSE和MAPE值如表3所示。

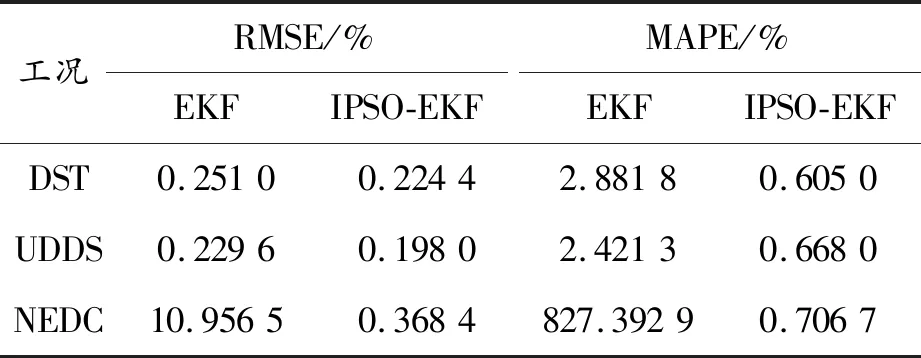
表3 DST、UDDS以及NEDC工况下EKF算法和IPSO-EKF算法的RMSE和MAPE值

由表3可知，DST工况以及UDDS工况下EKF算法和IPSO-EKF算法的RMSE值和MAPE值差别不大，这可能是由于DST和UDDS侧重模拟城市驾驶条件下动力电池的负载变化，电流激励比较单一，EKF和IPSO-EKF算法都具有比较好的适应性；但是在NEDC工况下出现了巨大的差距，EKF算法的RMSE值和MAPE值分别达到了10.956 5和827.392 9，而IPSO-EKF算法的RMSE值和MAPE值仅为0.368 4和0.706 7，这是因为NEDC工况包括4个市区工况小循环和1个郊区工况循环，需要兼顾城市和市郊驾驶条件下动力电池的负载变化，电流激励在市区循环和郊区循环之间切换时会发生比较大的波动，对算法的适应性提出了更高的要求，显然，IPSO-EKF算法的精度和适应性要优于EKF算法。

综合看来，相比于EKF算法，IPSO-EKF算法的RMSE和MAPE值更小，从统计学的角度来讲，具有更高的精度和可靠性；同时无论是偏向城市驾驶条件下动力电池的负载变化；还是兼顾城市和市郊驾驶条件下动力电池的负载变化，本文提出的IPSO-EKF算法均表现出很强的适应性。

5 结论

1)采用3阶RC等效电路模型，在不同放电倍率的基础上，利用离线辨识的方法辨识模型参数，试验与仿真结果表明，在离线参数辨识的情况下，3阶等效电路模型可以很好的进行模型参数识别。

2)本文所提出的IPSO-EKF融合算法，可以在EKF迭代过程中，利用IPSO优化系统噪声和观测噪声，提高SOC的估算精度。从试验和仿真的结果可知，相对于EKF算法，IPSO-EKF算法具有较高的估算精度和良好的适应性，无论是侧重于模拟城市驾驶条件下动力电池负载变化的DST工况和UDDS工况，还是兼顾城市和市郊驾驶条件下动力电池负载变化的NEDC工况，本文提出的算法都可以很好的进行噪声优化，提高SOC的估算精度。

3)本文提出的IPSO-EKF融合算法迭代速度较快，在5次左右的迭代过程中迅速收敛到全局最优位置，并且在随后的迭代过程中，最佳适应度值趋向于稳定。

4)相比于EKF算法，IPSO-EKF算法的RMSE和MAPE值更小，从统计学的角度来讲，具有更高的精度和可靠性；同时无论是偏向城市驾驶条件下动力电池的负载变化；还是兼顾城市和市郊驾驶条件下动力电池的负载变化，本文提出的IPSO-EKF算法均表现出很强的适应性。

5)除此之外，本文为其他类型的锂电池SOC估算提供了思路，即从噪声寻优的角度对SOC估算精度进行优化。