含初始变形的薄板十字形焊接接头疲劳强度评估

韩鑫宇 谌 伟 严仁军 邱 屿

(武汉理工大学船海与能源动力工程学院1) 武汉 430063) (高性能船舶技术教育部重点实验室(武汉理工大学)2) 武汉 430063)

0 引 言

十字形焊接接头广泛应用于海洋平台、船舶和桥梁中.随着钢结构薄板需求的增加，欧洲造船厂正在考虑减少游轮上部结构的结构重量，设计并使用超出船级社限制的更薄的甲板[1].然而焊接热输出引起的复杂轻型结构的变形已成为造船企业实现低成本制造的主要障碍，高强度薄钢材料的使用降低了上层甲板的重量，增强了承载能力，改善了结构性能和船舶稳定性，但增加了结构焊接初始变形的倾向[2].在大型薄板焊接结构中，制造引起的初始变形给薄板的切口应力场分析和疲劳强度评估带来了新的挑战.

初始焊接变形给薄板结构的应力场分析和疲劳评估带来的挑战主要体现在两个方面.一方面，薄板弯曲刚度较低，由焊接引起的变形不仅较之厚板要大，而且形状呈曲线[3]，会在焊趾处产生较大的应力集中，而传统的规范[4-6]推荐的计算焊趾处应力放大系数km值的公式均未考虑焊接初始变形的影响.为探讨焊接初始变形对薄板焊接接头焊趾处应力放大系数的影响程度，文献[7]引入局部角变形参量αL来量化薄板对接接头的初始变形，并对一系列考虑焊接初始变形的对接接头试件进行了试验.研究发现：薄板的矫直效果受试样的长细比和实际弯曲形状的影响很大；考虑初始变形，薄板的应力放大系数随着应力的增加在一定程度上得到缓解，但是应力集中现象更为突出.在此基础上，Shen等[8]对考虑初始变形的薄板对接接头进行了研究，将非线性有限元计算结果与规范公式计算结果对比发现：对于不考虑初始变形的薄板而言，规范公式与有限元计算结果较为吻合，但当局部角变形(初始变形)逐渐增大时，规范公式与有限元计算结果之间的误差也逐渐增大，该结论表明规范公式对于含初始变形的薄板接头应力场评估一定的局限性，且初始变形的存在会严重影响焊趾处的应力放大系数.

另一个挑战来自于薄板焊接接头疲劳评估的复杂性.文献[5]通过一系列实验研究发现焊接对船用薄板结构的疲劳寿命有明显的不利影响，主要是由于薄壁结构的疲劳强度对制造和装配引起的缺陷比较敏感[9]，微小的焊接缺陷也会对薄板焊接结构的疲劳强度产生较大的影响[10].而且与厚板相比，薄板焊接接头的疲劳实验数据离散性更大，因此，薄板焊接结构在疲劳强度评估中需要使用局部方法，如结构应力方法或切口应力方法.Sonsino等[11]基于切口应力方法对一系列薄板焊接接头的实验数据进行了疲劳评估，发现薄板焊接接头的疲劳寿命S-N曲线斜率的负倒数为5，比规范推荐值3要大.

综上所述，在进行薄板焊接结构的应力场和疲劳评估时必须考虑初始焊接变形和几何非线性的影响[12].因此，在薄板对接接头焊趾处的应力集中系数公式的基础上，文中针对十字形焊接接头，对文献[13]提出的公式进行了修正，使其适用于计算含初始变形的十字形加筋结构焊趾处的应力放大系数.将传统规范公式计算结果、非线性有限元计算结果以及本文修正公式的计算结果进行了对比，并结合切口应力方法，运用修正公式对一系列含初始焊接缺陷的十字形接头试件进行了疲劳评估，以此来验证修正公式对十字形试件焊趾处应力放大系数公式计算和疲劳性能评估的准确性.

1 应力放大系数公式推导

1.1 规范公式

切口应力方法是一种基于线弹性理论的局部应力方法，除了能考虑试件几何尺寸和焊缝几何形状的影响外，还可以考虑焊接错位和焊接变形的影响.切口应力可在名义应力的基础上乘以应力放大系数得到.

K=σnotch/σnom=kg·kw·km

(1)

式中：kg、kw为几何形状和几何尺寸的应力集中系数，kw·kg=0.9+0.9(tanα)0.25；km为考虑焊接错位和焊接角变形的应力集中系数，km=kte·ktα；其中：kte为焊接错位引起的应力集中系数；ktα为焊接角变形引起的应力集中系数.

在十字形焊接接头中，焊接热输入会使焊接试件产生明显的焊接角变形，见图1.

图1 厚板十字形焊接接头

对于无初始变形的厚板焊接试件，文献[10]给出了由焊接角变形αG引起的焊趾处的应力集中系数ktα表达式为

(2)

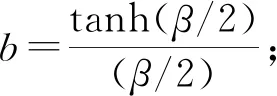
1.2 薄板焊接接头

规范给出的应力放大系数计算公式仅适用于无初始变形的厚板焊接接头，对于板厚小于5 mm的薄板而言，由于弯曲刚度较低，除了焊接错位和整体角度变形外，薄板焊接结构在焊接过程中还会伴随初始变形的出现，见图2.文献[6]首先引入参数对初始变形进行了量化，并对考虑初始变形的对接接头研究发现：初始变形对焊接试件焊趾处的应力放大系数存在影响，随着初始变形的增加，应力放大系数也会随之增加，但当前的规范公式在计算焊趾处的应力放大系数时未考虑初始变形的影响，在求解薄板焊接接头焊趾处的应力放大系数和进行疲劳评估时会带来较大的误差.因此本文综合考虑如图2所示的焊接整体角变形和初始变形的影响，对薄板焊接十字形试件焊趾处的应力集中系数进行了推导.

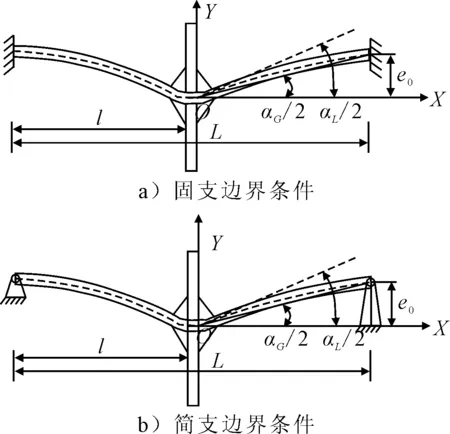
图2 考虑初始变形的薄板十字形焊接接头

假设试件无外力作用时的变形为，有拉伸荷载作用而引起的变形为，总变形为，则有ym=y0+y.

以十字形接头肘板与主板的交点为坐标原点，选取图3的力学模型进行分析，根据力和弯曲的平衡可得dV/dx=0：

图3 薄板十字形接头中的微观力学模型

(3)

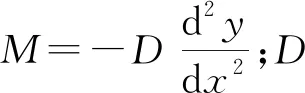
引入量纲-的量参数:

(4)

式中：e0试件约束端距横坐标的距离.

联立式(3)～(4)并考虑对称情况可得：

(5)

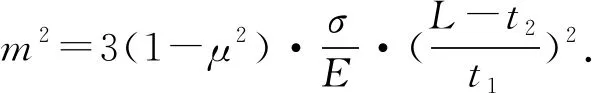
(6)

(7)

式(5)的通解为计算角变形和初始变形引起的应力放大系数的关键，为使式(5)具有可解性，将无荷载作用时板的曲线方程简化为二次函数，可得η0为关于横坐标x的方程为

η0=(1-C)ξ2+Cξ

(8)

将式(8)带入式(5)得方程的通解为

ζ=C1-Cξ+C2exp(-mξ)+

C3exp(mξ)+(C-1)ξ2

(9)

在固支边界条件下,

(10)

在固支边界条件下，即可得弯曲附近应力系数.

(11)

2 数值分析

2.1 试件几何参数

为了考虑初始变形对应力放大系数的影响，运用有限元计算软件Ansys 16.0对图4的板厚为4 mm的一系列薄板十字形焊接试件进行了计算，试件各尺寸参数见表1.材料弹性模量为2.1×105MPa，泊松比为0.3.

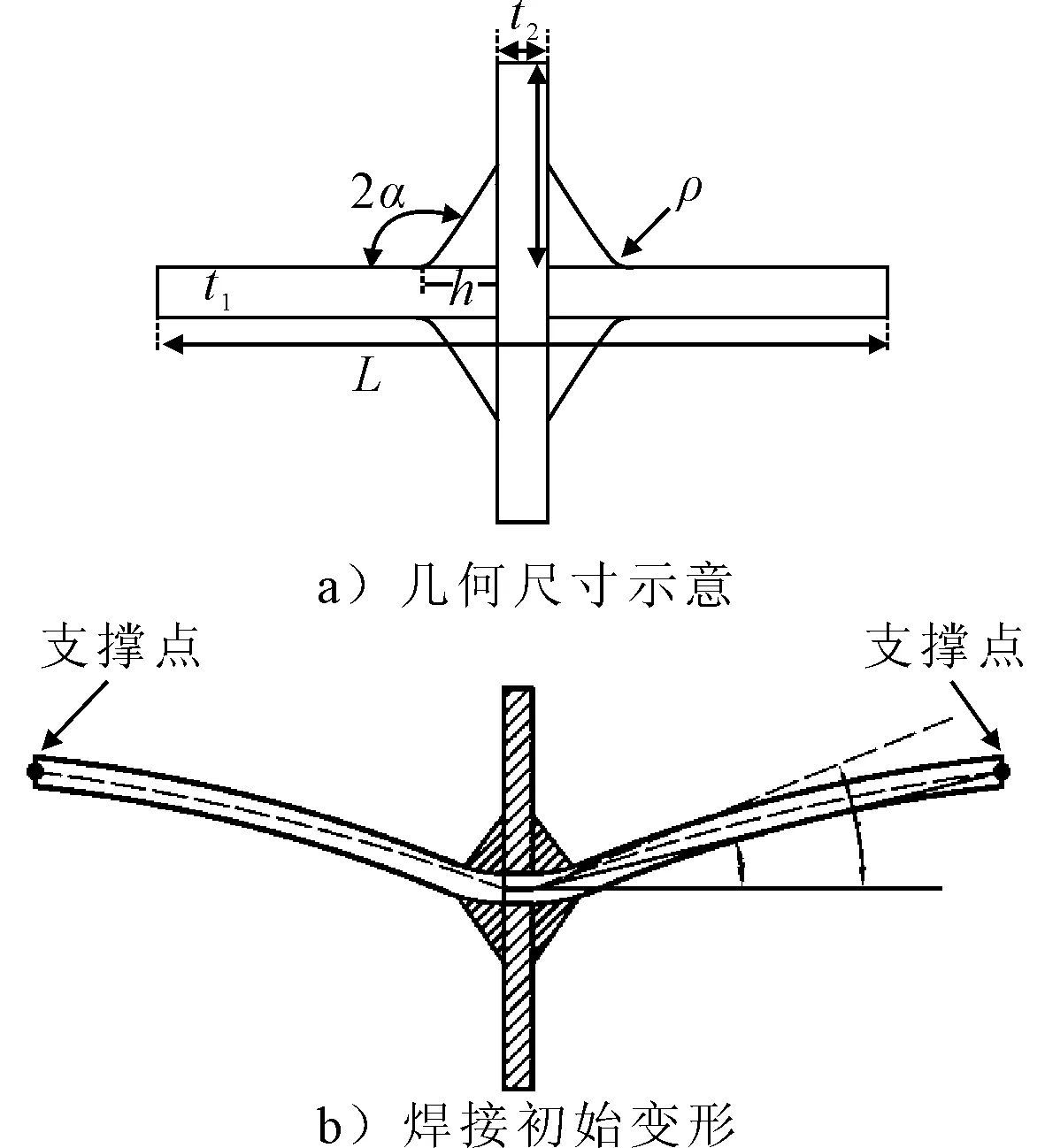
图4 十字字型焊接接头

表1 焊接接头的几何尺寸取值

2.2 有限元分析

考虑焊接角变形，可通过非线性有限元方法计算初始变形引起的应力放大系数，由于焊接接头焊趾处的实际半径约为1 mm，因此在有限元建模中，焊趾处的虚拟半径取值为1 mm，并采用Solid 186单元建立了十字形试件的有限元模型，见图6a).同时，分别考虑简支边界和固定边界，数值方法中的应力放大系数可以表示为

σnotch=km·kw·σnom=kw·σHS

(12)

式中：km=σHS/σnom，σHS为热点应力，通过线性差值得到.

为提高有限元计算结果的计算精度，首先开展网格收敛性分析.以整体角变形αG=4°,αL/αG=2，且受100 MPa均布荷载和固支边界条件作用的十字形试件为例，图5b)为焊趾处不同单元大小对应的从焊趾沿x方向节点的轴向应力分布图.由图5b)可知，当焊趾处的单元的大小为0.1 mm时，焊趾附近的应力场不再发生改变，因此本文焊趾处的单元大小取值为0.05 mm，同时该值也小于文献[10]规定的最小单元大小ρ/4=0.25 mm.

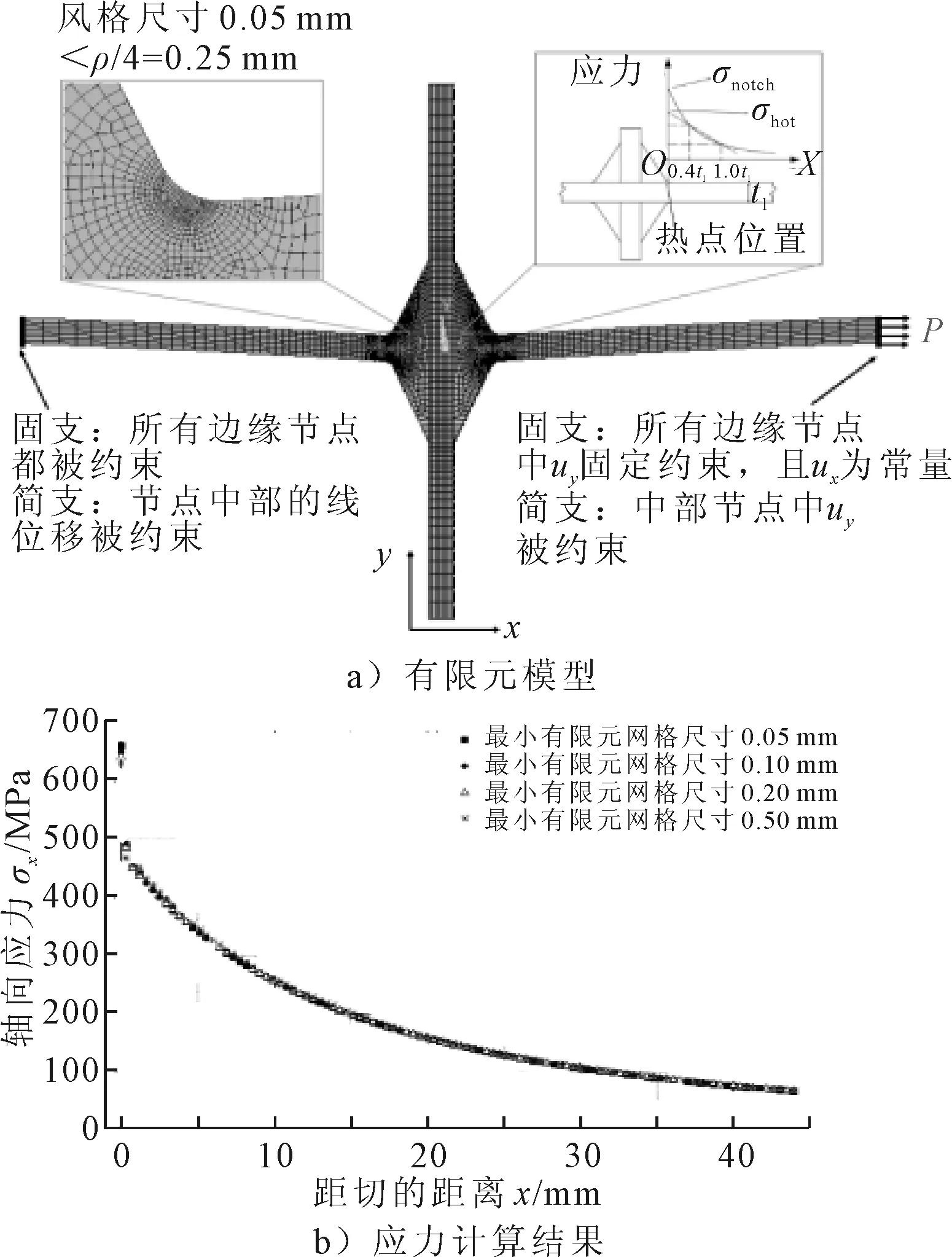
图5 单元收敛性分析

通过改变结构角变形比例αL/αG，可由非线性有限元方法计算得到不同几何尺寸下十字形节点的热点应力及应力放大系数.以名义应力αnom=50 MPa时的应力结果作为参考，图6分别为αL/αG=1和αL/αG=4时固支和简支两种边界条件下x方向的应力结果对比.由应力对比结果可知：在αL/αG=1时，固支边界条件与简支边界条件下的x方向应力相差较大，随着角变形比例αL/αG的增加，两种边界条件下的x方向应力场分布趋于一致，主要原因是：荷载值越大，在相同应力增量下引起的矫直效果越弱；而且随着角变形比例αL/αG的增加，焊趾处的应力结果也会随之增加.因此，薄板十字形接头的初始变形对焊趾处的应力集中效应有较大影响，有必要考虑薄板初始变形对焊趾处应力放大系数的影响.

图6 十字形试件沿x方向的应力场分布

2.3 修正公式的误差分析

2.3.1αL=αG

为考虑薄板初始变形的影响，本文对焊趾处的应力放大系数公式进行了推导(以下统称为修正公式).当无初始变形时，规范公式能准确的计算由焊接角变形引起的焊趾处的应力放大系数.为验证本文修正公式(7)对于计算无初始变形试件应力放大系数的准确性，将有限元计算结果、规范公式(2)和修正公式(7)的计算结果进行对比，见图7.由图7可知，在不考虑初始变形时，三种方法的计算结果均比较相近，规范公式(2)和修正公式(7)与有限元计算结果之间的误差均在10%以内.

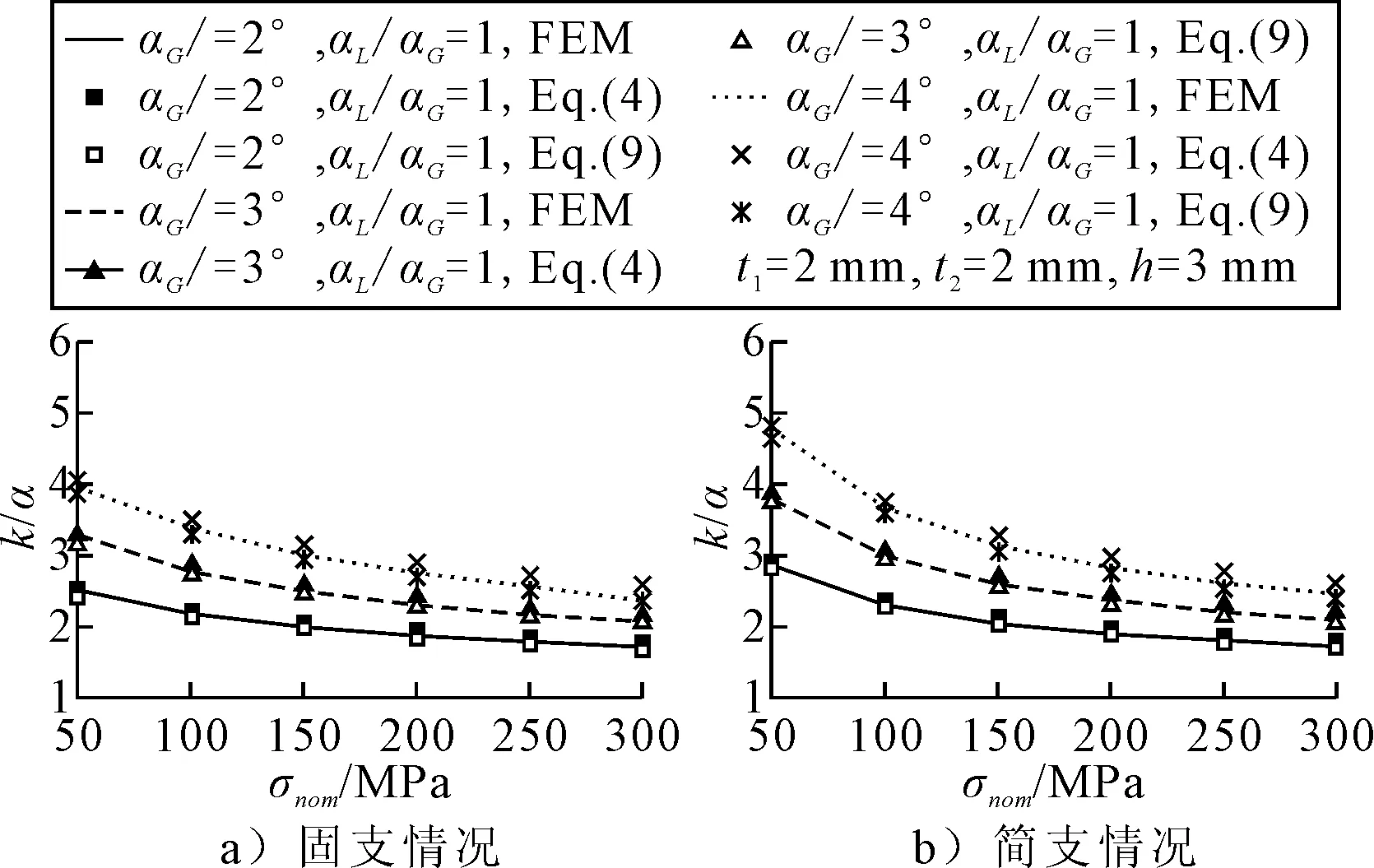
图7 公式计算结果与有限元计算结果对比

2.3.2αL≠αG

传统规范公式(2)在进行焊趾处的应力放大系数求解时未考虑初始变形αL的影响，而研究表明，初始变形会对焊趾处的应力放大系数产生较大的影响.本文以固支情况下的试件作为例，分别运用有限元方法和规范公式(2)对不同角变形下试件焊趾处的应力放大系数进行了计算，结果见图8.由图8可知，考虑初始变形时，规范公式(2)的计算结果与有限元计算结果之间误差较大；当αL/αG=4时，规范公式(2)的计算结果与有限元计算结果之间的误差基本上在30%以上，随着角变形比例αL/αG的增大误差会越来越大.

图8 有限元方法与规范公式计算的ktα对比

为验证本文公式的准确性，将αL≠αG时的有限元计算结果与公式(9)计算结果进行对比，见图9.考虑不同角变形比例αL/αG，本文公式计算得到的十字形焊接试件焊趾处应力放大系数与有限元计算结果比较相近，误差均在10%以内，因此，本文公式可以有效考虑初始变形对薄板十字形试件焊趾处应力放大系数的影响.

图9 修正公式与有限元计算结果对比

3 疲劳强度评估

为验证本文公式对含缺陷薄板焊接接头的疲劳性能，基于切口应力方法，将本文修正公式(7)推广到各类典型接头：T形接头、十字形接头和对接接头.选取一系列薄板试件的疲劳数据开展薄板结构切口应力场和疲劳评估.试件厚度为3～5 mm，弹性模量E=2.1×105MPa，泊松比μ=0.3，具体材料及尺寸参数见文献[14].

图10为分别运用名义应力方法、传统规范公式和基于本文修正公式的切口应力方法的疲劳评估S-N曲线，由图10可知，基于本文修正公式的切口应力方法得到的分散带指数Tσ=2.26要明显小于名义应力(Tσ=2.66)和传统公式结果(Tσ=2.44).在考虑初始变形的情况下，运用修正公式(7)来更能有效的评估薄板焊接接头的疲劳强度.

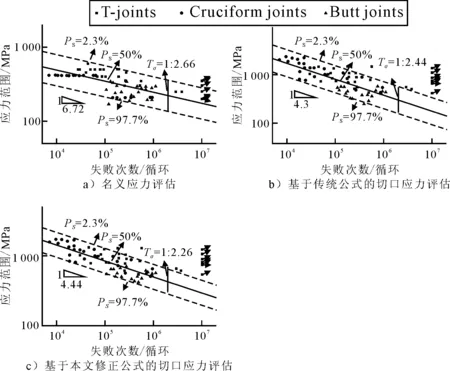
图10 薄板焊接接头的疲劳强度评估

基于修正公式(7)得到存活率50%时对应的S-N曲线为

lgN=18.00-4.44lgS

(13)

在疲劳寿命Nref=2×106次对应的疲劳强度为433.84 MPa，曲线斜率的负倒数为m=4.44，与文献[14]得到的5较为接近，验证了本文修正公式的有效性.

4 结 论

1) 文中考虑初始焊接变形，对十字形焊接试件焊趾处的应力集中系数公式进行了推导并将其运用到焊接试件的疲劳评估中.对比发现：该修正公式考虑初始变形的影响，对于不同角变形比例αg/αL的试件，本文修正公式均能准确地计算十字形试件焊趾处的应力放大系数，其计算结果与有限元计算结果之间的误差均在10%以内，满足工程实际的误差要求.

2) 运用文中修正公式，在对不含初始变形的厚板焊接试件和考虑初始变形的薄板焊接试件进行疲劳评估时能有效的降低疲劳评估的分散带指数.相比名义应力评估结果，薄板试件的切口应力S-N曲线的分散带指数从2.66减小至2.26，可以有效提高薄板焊接结构的切口应力场和疲劳评估精度.