基于DPSO-ANFIS的大坝变形预测模型

马广臣 ，杨 杰 ，程 琳 ，宋锦焘

(1. 西安理工大学 水利水电学院，陕西 西安 710048； 2. 西北旱区生态水利工程国家重点实验室，陕西 西安710048)

随着社会经济发展，现代水利工程技术不断革新，修建水库大坝成为当前水利工程的主体内容之一。修筑大坝耗费高、工程量大、工程周期长，带来效益的同时也存在高风险。水库大坝一旦失事，会造成重大事故与损失，需对大坝进行安全监控，而利用大坝实际监测数据建立变形预测模型是大坝安全监控的内容之一。针对具有复杂非线性特征的大坝变形监测数据[1]，自适应模糊神经网络系统（Adaptive Network-based Fuzzy Inference System，ANFIS）具有结构和参数辨识的特点，可以自适应生成模糊规则，优化隶属和输出函数。该系统依据输入影响因素，可自动设计系统参数，实现模糊系统自学习，对非线性系统适用性较好，在大坝安全监控方面具有良好应用前景。

20世纪中期，国外学者[2-4]在大坝变形预测模型方面做了大量工作。我国学者吴中如[5]、何金平等[6]在大坝监测数据分析方面进行了深入研究，建立了3种大坝变形监控模型，即统计模型、确定性模型、混合模型。随着科学技术发展和各种新学科的出现，学科交叉融合不断形成解决实际问题的新方法。混沌理论、模糊数学、神经网络、粒子群算法、遗传算法及其他生物种群算法等理论方法已广泛应用于大坝监测资料的分析之中，大坝变形预测模型日趋丰富。黄世秀等[7]运用小波消噪及反向传播（Back Propagation，BP）神经网络方法建立大坝变形预测模型，提高了神经网络的计算效率；何政翔等[8]将模糊聚类方法运用到大坝变形监测数据分析中，建立多元逐步回归统计模型进行大坝变形预测；钟登华等[9]采用自适应模糊神经网络推理系统优化灰色理论模型的建模方法来预测大坝变形；文献[10]根据不同堆石坝运行期的沉降观测数据建立自适应模糊神经网络模型，提高了预测精度。

大坝变形是复杂的非线性问题，在处理大坝监测数据进行非线性分析过程中，上述模型还存在预测精度不高、泛化性能一般等问题。鉴于此，将自适应模糊神经网络引入到大坝变形预测模型中，通过动态权重粒子群算法（Dynamic Weighted Particle Swarm Optition，DPSO）对自适应模糊神经网络模糊层的适应度值进行寻优，形成可以寻找最优适应度值的自适应模糊神经网络，进而建立具有预测精度高、泛化性能好、稳定性可靠的基于DPSO-ANFIS的大坝变形预测模型。

1 ANFIS模型

ANFIS是将模糊数学与神经网络相结合，具有自适应学习能力和模糊系统易于表达知识的特点。根据大量数据，通过自适应建模生成模糊推理系统（Fuzzy Inference System，FIS），根据误差准则修正隶属函数参数，使FIS模仿进而提供训练数据[11]。以单阶Sugeno型模糊系统的推理过程为例，对于两输入单输出模型，其结构如图1所示。

第一层：输入层。将实际数据作为样本输入，经过模糊化处理以后，输出对应的隶属度。

第二层：模糊规则层。计算出每条规则的适应度，把所有输入信号累乘。

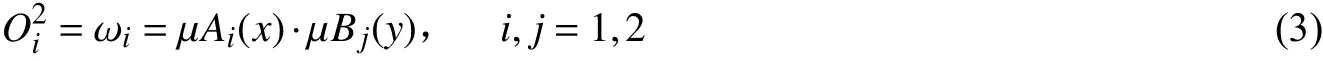
第三层：归一化层。对每条规则的适应度进行归一化计算。

第四层：计算输出层。计算每条规则的输出结果。

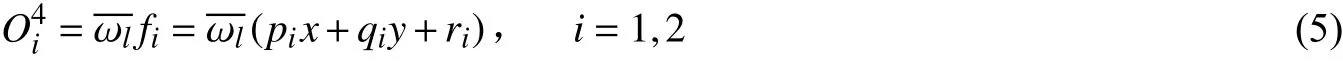
第五层：总输出层。计算整个模糊系统的总输出。

在数据模糊化处理中，ANFIS的训练结构包括网格分类与减法聚类。本文采用减法聚类，参数取值如下：影响半径为0.3，最大迭代次数为200，目标误差为0.000 1，初始步数为0.01，步长减小率为0.9，步长增长率为0.1。

2 动态权重粒子群算法

粒子群算法是目前常用的一种迭代算法，其思想来源于对鸟群捕食行为的研究。算法通过迭代寻优，搜索个体最优位置Pb和 群体最优位置Gb， 最终得到最优粒子。粒子群算法表示如下：在一个N维搜索空间中，一个种群由m个粒子组成，由矩阵Z表示。第i个粒子的位置用Zi表 示。第i个粒子的速度表示为：

式中：ViN表示第i个 粒子在第N维的速度，随着每次迭代的运行，粒子通过个体和全局最优值来更新自身的速度与位置，更新计算式如下：

表1 粒子群算法参数取值Tab. 1 Parameter values of particle swarm optimization algorithm

惯性权重在整个算法体系中非常重要，可以改变全局和局部搜索能力。Shi等[12]提出了线性递减惯性权重，而粒子群算法中的ω通常取值0.4～0.9，由于采取线性递减，使得ω随迭代次数的增加而减小，易在全局最优解附近产生早熟和震荡现象。为此，采用一种自适应权重的方式对算法中的ω进行改进[13-14]，改进后的惯性权重计算如下：

式中： ωmax,ωmin分 别为惯性权重的最大与最小值；f为粒子当前适应度值；fmin,f¯分别为当前所有粒子的最小适应度值与平均适应度值。

3 基于DPSO-ANFIS的大坝变形预测模型

依据大坝实际监测数据，以环境因素为输入条件，大坝变形数据为输出结果，建立大坝变形预测模型。大坝变形有众多因素，包括环境、水位、材料特性、结构形式、外界荷载作用等等。由大坝变形监控的统计模型及其混合回归模型[15-16]，可得大坝变形主要因素包括静水压力、温度及时间效应。大坝变形预测模型的表达式为：

式中：y为大坝水平向位移；H为上下游水位差；T为温度；θ为时效。

在统计模型中，大坝变形位移由水压、温度及时效组成：

式中：yH为水压位移；yT为温度位移；yθ为时效位移。

对混凝土坝体变形而言，取相关变形影响因子共9个，建立基于DPSO-ANFIS的大坝变形预测模型。其中水压因子取3个，分别为H、H2、H3；温度因子取4个，分别为距观测日期前5天、前20天、前60天、前90天的平均气温T5、T20、T60、T90；时效因子取2个，即 θ 和lnθ（θ表示监测日期至初始监测日期的累积天数除以100）。模型构建含以下6个步骤。

步骤1：采集大坝变形监测实际工程数据，并进行预处理，通过影响因素所占比重来确定模型输入变量及其个数。

步骤2：选择ANFIS模型的聚类算法及其初始参数，同时初始化粒子群参数（包括种群大小、粒子初始速度与位置、迭代次数、误差精度、惯性权重等）。

步骤3：提取ANFIS模糊层的适应度值，然后将其作为粒子群初始化的待优化参数，进而求解空间初始化粒子群。

步骤4：计算每个粒子的适应度值，同时更新个体粒子局部最优与所有粒子全局最优值。

步骤5：更新惯性权重值并且通过式（8）、（9）更新粒子的速度与位置。

步骤6：判断是否满足精度要求或者达到最大迭代次数。若满足，则输出模糊层的最优适应度值，代入ANFIS模型进行数据训练，最后输出预测结果；若不满足，则返回步骤4。

模型的性能评价是预测模型可靠、实用的前提，其误差的适当估计能评价不同模型的准确性。为了对比模型的预测结果及实测数据的偏差，本文采用3个性能指标评价模型的预测精度，即相关系数R、均方根误差eRMSE和平均绝对误差eMAE。相关系数值越接近1表明两者之间的线性相关性越强，均方根误差与平均绝对误差值越小，表明模型精度越高。

4 工程实例应用

某水电站地处福建省境内，属于引水式电站，电站包括混凝土大坝、厂房系统、变电站系统、输水系统及泄水建筑物。大坝分为溢流段和挡水段两部分。大坝变形监测项目包括坝顶水平位移和垂直位移。本文采用坝顶水平位移引张线法所测数据进行分析，建立大坝变形预测模型。大坝的结构和测点布置见图2。

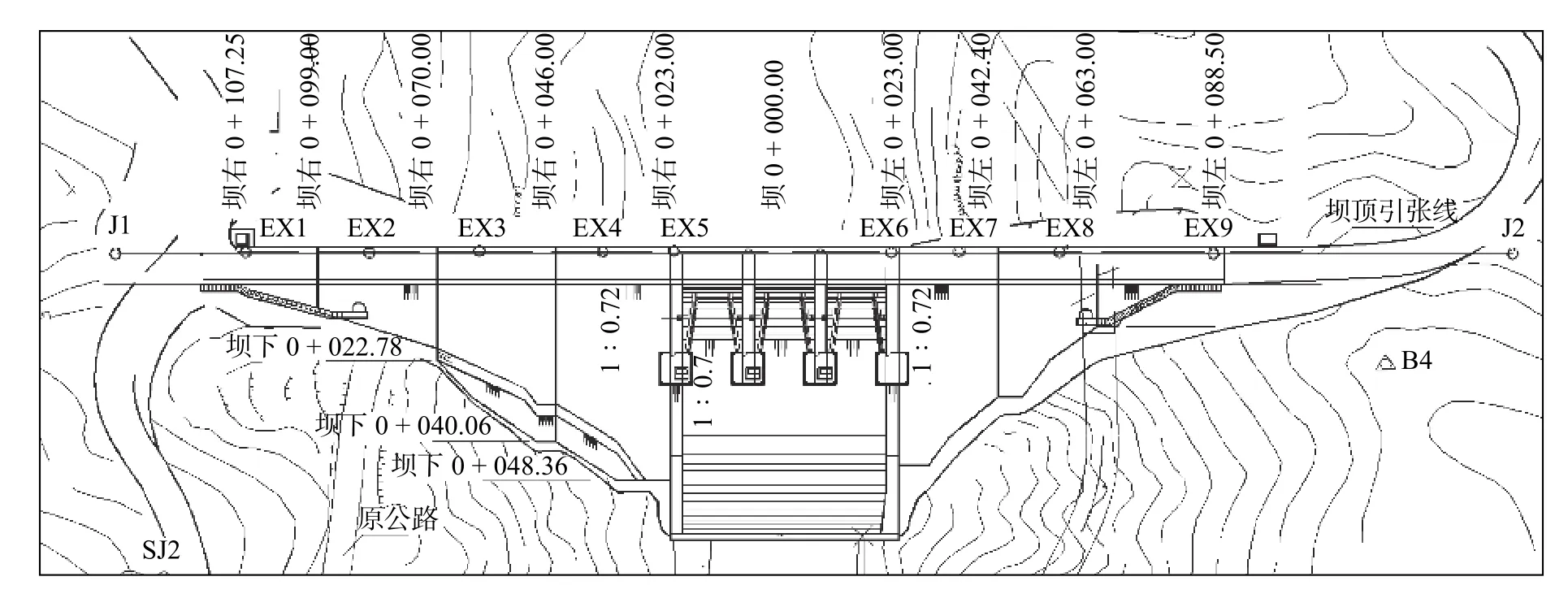
图2 大坝的测线布置Fig. 2 Survey line layout of the dam

4.1 模型训练与预测

选取大坝坝段编号为EX1、EX5、EX7测点的监测数据作为数据样本，监测频率为每天1次。这个时间 序 列包含2016年6月2日至2017年9月13日共计470组数据。把前380组数据作为训练样本，分别以后面10组、30组、50组、70组、90组数据作为预测样本，用于检验模型预测的精度。大坝坝段编号EX1、EX5、EX7测点的引张线水平位移过程线如图3所示。

图3 EX1、EX5、EX7测点水平位移过程线Fig. 3 Horizontal displacement process lines of measurement points EX1, EX5 and EX7

对前380组数据进行模糊化训练，这里以预测30组结果为例，将不同测点不同模型的预测结果进行整理，如图4所示。针对不同预测时间序列，各测点在不同模型中的预测值见图5。

图4 不同模型预测结果对比Fig. 4 Comparison of prediction results and measured results of different models

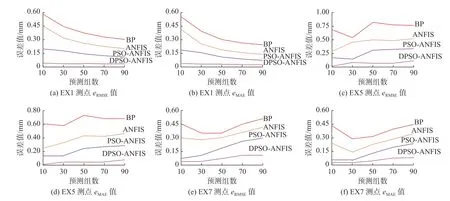
图5 各测点在不同模型、预测时间序列下精度值的趋势Fig. 5 Trend chart of precision values of each measuring point in different models and prediction time series

4.2 模型性能评价

为了准确评价模型精度，体现自适应模糊神经网络在大坝变形预测方面的适用性，对比了ANFIS模型、PSO-ANFIS模型及BP神经网络模型[17]，各测点的性能评价指标见表2。

表2 不同模型各测点性能评价Tab. 2 Performance evaluation table of each measurement point in different models

分析图4、图5和表2数值可得：在模型精度评价指标方面，有关ANFIS模型的相关系数都在0.88以上，表明实测值与预测值相关性较好，而BP模型的相关系数最差的为0.80，二者相关性一般。在均方根误差和平均绝对误差值方面，DPSO-ANFIS模型数值小于其他模型，反映出该模型的预测精度较高。在不同位置测点，DPSO-ANFIS模型预测效果较好，预测趋势符合实测数据走向，精度也优于其他模型，表现出良好的泛化性。在预测时间序列方面，随着预测天数的增加，在EX1测点中，DPSO-ANFIS模型预测效果好，整体预测性能稳定，其余3种模型表现为预测精度提高。在EX5、EX7这两个测点中，所有模型表现出随着预测天数增加而预测精度降低的趋势。DPSO-ANFIS模型在3个测点的预测效果中表现较好，而且预测精度在合理范围内，并优于其他模型。

5 结 语

采用动态权重粒子群算法优化自适应模糊神经网络中模糊层的适应度值，形成可以寻找最优适应度值的自适应模糊神经网络，结合实际工程监测数据，建立了基于DPSO-ANFIS的大坝变形预测模型，得到了如下结论：

（1）将自适应模糊神经网络引入到大坝变形预测模型中，采用动态权重粒子群算法对自适应模糊神经网络进行优化，可提高模型预测精度。

（2）对比传统BP神经网络和ANFIS两种模型，动态权重粒子群算法优化后的自适应模糊神经网络模型弥补了标准粒子群算法优化程度不够、预测精度不高的缺点。同时该模型在不同位置测点、预测时间序列中表现出较好的性能，整体稳定性与预测效果优于其他模型，可以用于大坝的变形预测。

文中提出的基于DPSO-ANFIS的大坝变形预测模型还存在一些不足之处。首先，自适应模糊神经网络层数较少，数据训练程度一般，后面可以考虑将深度学习神经网络引入到大坝变形预测模型中。其次，在模型数据预处理上，采用模糊化处理，对不同算法及不同坝型可考虑制定模型所需数据的适用标准。