基于GWO-LSTM的丹江口水库入库径流预测
王立辉,杨辉斌, ,王银堂,刘 勇,胡庆芳
(1. 福州大学 水利水电与港口工程系,福建 福州 350116; 2. 南京水利科学研究院 水文水资源与水利工程科学国家重点实验室,江苏 南京 210029)
径流预测在水文预测预报中占有重要比例,做好径流预测对防洪抗旱、水资源利用及水库调度具有重要的指示作用。目前应用较为普遍的径流预测方法大致有两种:一是水文模型;二是数据驱动模型。前者是具有明确产汇流机制的水文过程的模拟和概化,而后者则是基于数据之间的统计关系驱动的数据分析模型。由于部分水文资料获取难度较大,水文模型受到一定限制,而数据驱动的机器学习模型近年来在水文预报领域得到高度关注。如人工神经网络[1-2]、决策树、支持向量机[3-4](Support Vector Machine, SVM)、随机森林[5](Random Forest, RF)及目前应用较多的长短期记忆网络(Long Short-Term Memory, LSTM)。相对传统结构较为单一的人工神经网络在预测过程中容易存在“过拟合”问题,LSTM模型在结构上进行了改进,不仅有效改善了这一问题,而且也部分解决了循环神经网络中“梯度爆炸”和“维度灾害”问题,使其得到广泛应用[6-8]。在水文预报领域,Kratzert等[9]基于CAMELS数据集使用LSTM模型对241个水文流域进行降雨径流测试,结果表明LSTM能够通过气象观测数据预测径流,其性能可与SAC-SMA与Snow-17的耦合模型媲美。冯钧等[10]将LSTM应用于鄱阳湖的日径流预测,并与人工神经网络(Artificial Neural Network, ANN)和the Soil & Water Assessment Tool (SWAT)对比,发现LSTM有较好的预测性能。殷兆凯等[11]基于LSTM进行降雨径流模拟及预报,发现LSTM在短预见期内优于新安江模型,同时隐藏层神经元数量既会影响模型预报精度,也会影响模型训练速度。然而在一系列学习模型中,对网络结构超参数的选取一直没有明确的定义,而它们又是机器学习的重要组成部分,因为它们会对模型的性能产生重大影响[12]。网络结构超参数是机器学习方法在开始训练前设置的参数,不同取值会带来不同的预测效果,是机器学习方法中的重点和难点。因此,提出了许多优化超参数的算法,如网格搜索[13]、粒子群优化算法[14](Particle Swarm Optimization, PSO)、随机搜索[15]、灰狼优化算法[16](Grey Wolf Optimizer, GWO)等。传统的网格搜索及随机搜索等计算量较大,且易陷入局部最优的结果。而GWO是模仿狼群社会生活的一种启发式优化算法,具有收敛快和全局遍历性的特点,Pan等[17]以马尔可夫过程(Markov process)证明了灰狼优化算法的全局遍历性特点,并结合LSTM模型实现机载燃油泵寿命的预测,具有较好的预测效果。Rashid等[18]对比了GWO与其他优化算法优化LSTM的应用效果,发现GWO优化LSTM效果较好。胡孟婷[19]在软件定义网络(SDN)网络流量态势预测中对比了GWO优化的LSTM与BPTT优化的LSTM,发现GWO优化的LSTM模型具有更好的预测效果及收敛快等优势。因此,本文在此基础上构建灰狼长短期记忆模型(GWOLSTM)及灰狼人工神经网络(GWO-BP),以丹江口水库月入库径流进行实例研究,初步探讨GWOLSTM模型在水文预测方面的应用效果,为丹江口水库月入库径流预测提供技术参考,同时对网络超参数的选取提供参考。
1 研究方法
1.1 LSTM模型原理
LSTM是一种特殊的循环神经网络,与传统循环神经网络的区别在于在网络结构中添加了具有记忆功能的单元。图1展示了LSTM模型记忆单元的典型结构。LSTM有4个处理信息的“门”(分别是遗忘门f、输入门i及 输出门o和一个独特的记忆细胞c)。

图1 LSTM网络记忆单元结构示意Fig. 1 Schematic diagram of one LSTM memory block
具体处理过程如下:
(1)在t时刻,有两部分输入,分别是前一时刻的输出结果ht-1和 这一时刻的新输入信息xt。首先计算遗忘门f,遗忘门控制输入信息有多少将被遗忘。计算式如下:

(2)计算输入门i,输入门控制有多少输入信息将参与细胞的更新。计算式如下:


(4)对之前的细胞状态ct-1进 行更新,细胞状态c是LSTM模型的关键。计算式如下:

(5)计算输出门o, 输出门控制有多少信息将用于生成ht。计算式如下:

(6)将ht传输到输出层,输出y。计算式如下:

式中: σ(·)为 Sigmoid函数; t anh(·)为 双曲余弦函数;W、U为权重矩阵;b为偏置向量;⊙为向量标量积;y为t时刻的输出。
1.2 GWO算法原理
灰狼优化算法[17](Grey Wolf Optimizer, GWO)通过模仿自然界中狼群狩猎的生活方式来实现目标的最优化。在寻找猎物中,狼群被分为4个社会等级,第一个等级被称为头狼,用 α表示;第二等级的狼用β表示,它服从于α 狼;第三等级的狼用δ 表示;最后底层被称为ω狼,服从其他层次的狼。
围猎过程如下:
(1)首先,对猎物进行包围:

式中:j为当前的代数;A、C为 协同系数向量;Xp为 猎物的位置向量;X为灰狼的位置向量;D为灰狼与猎物之间的距离。
其中A、C的计算方式如下:

式中:a随 着迭代次数增加,从2线性递减到0;r1、r2为[0,1]的随机数向量。
(2)对猎物进行抓捕:实际上由于不知道猎物的位置,即不知道目标的最优值在哪里。因此假设α 是最靠近猎物的,β 、δ 其 次,式(12)用来计算它们与猎物的距离。通过不断更新α 、β 、δ狼的位置(式(13)),来号召其他灰狼不断靠近猎物(式(14)),最后认为α 狼的位置即是猎物的位置。其计算式如下:

式中:Xα(j)、Xβ(j)、Xδ(j)为j代时α 、β 、δ的位置。
1.3 GWO-LSTM模型
利用GWO具有全局遍历性的优点对LSTM的初始权重、阈值和隐藏层神经元数进行自动寻优,避免人工调参耗费大量的时间及陷入局部最优的结果。其耦合过程如图2。

图2 GWO-LSTM流程Fig. 2 Flow chart of GWO-LSTM
2 研究区域及数据介绍
选取汉江中上游丹江口水库区域作为研究对象。丹江口水库是中国南水北调中线工程的水源地,属国家一级水源保护区,总面积846 km2,有“亚洲天池”之美誉,是汉江的天然水位调节器。丹江口水库多年平均入库水量为394.8亿m3,水源来自于汉江及其支流丹江。以丹江口水库1952—2008年的9月份和10月份的月入库径流资料作为预测对象。由于丹江口水库水域位于华西秋雨区,其秋汛期9、10月总径流量占主汛期径流量的47.7%[20]。预测因子资料采用中国国家气候中心计算的74项主要环流特征量数据、海温数据(50°N~10°S,120°E~80°W格点数据)、丹江口水库上游流域面降雨量(图3)、NCEP再分析资料500 hPa和100 hPa两个等压面的位势高度场(全球格点数据144×73),NCEP再分析资料是美国国家环境预测中心(National Centers for Environmental Prediction, NCEP)和大气研究中心(National Center for Atmospheric Research, NCAR)(https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.html)的数据产品。时间尺度为1952—2008年的逐月资料,共57年,将总长度的80%作为训练期,20%作为验证期,即1952—1996年为训练期,1997—2008年为验证期。

图3 丹江口水库流域示意Fig. 3 Schematic diagram of Danjiangkou Reservoir
3 GWO-LSTM模型构建
本文采用刘勇[20]的因子筛选方法对丹江口水库月入库径流预测因子进行筛选,即采用单相关系数及随机森林重要性分析丹江口水库月入库径流与预测因子之间的相关关系,综合相关系数及属性重要度,最终确定9月份的预测因子为7个,10月份的预测因子为6个,具体预测因子见表1。因此,模型的输入层数分别为7和6,根据不同月份进行选择。由于LSTM结构的复杂性,将LSTM隐藏层层数设置为1,其隐藏层神经元数目、初始的权值和阈值利用GWO优化确定,其中神经元数的取值范围为[3,50],初始权值和阈值的取值范围为[-1,1]。模型的输出层数为1,模型的训练次数设置为100,模型损失函数为均方误差。在隐藏层后面增加一层舍弃层,防止模型出现过拟合。模型训练过程采用Adam算法进行优化,搭建在MATLAB平台下实现。同时设置狼群数量为20,最大迭代次数为20次,优化中适应度采用均方根误差,并且综合考虑训练期和验证期的均方根误差,设置权重为0.5和0.5。

表1 9月和10月预测因子Tab. 1 The forecast factors of September and October
模型的评价标准采用均方根误差(Root-Mean-Square Error,ERMS)和纳什效率系数(Nash-Sutcliffe Efficiency Coefficient,ENS),ERMS越 小表明误差越小,ENS越接近1表明过程吻合性越好。Ritter等[21]指出一般ENS大于某一个值时,认为模型的预测效果是可以接受的,这个值的范围为0.50~0.65。
4 结果分析
4.1 模型对比分析
利用GWO-LSTM模型、GWO-BP模型和逐步回归模型对丹江口水库1952—1996年9月份和10月份的入库径流进行训练,1997—2008年9月份和10月份的入库径流进行验证。其训练期和验证期的ERMS和ENS结果见表2。

表2 不同模型对应的丹江口月径流预测精度指标Tab. 2 Accuracy of monthly runoff prediction of Danjiangkou corresponding to different models
对比3种模型在丹江口水库月入库径流预测的应用效果,可以看到在同样条件下,无论在训练期还是验证期,GWO-LSTM模型的均方根误差ERMS都 低于GWO-BP和逐步回归模型,且其纳什效率系数ENS都高于GWO-BP和逐步回归模型,这说明相对于传统神经网络模型,拥有“记忆”结构的LSTM模型在预测方面更具优势。再将LSTM、BP两种非线性模型与逐步回归模型相比,可以看到非线性模型对复杂的水文预测系统来说有更好的预测效果。
3种模型训练期及验证期的预测效果见图4,图中出现的负值应将其处理为零,本文暂不处理。从中发现,对于整体趋势预测能力,GWO-LSTM>GWO-BP>逐步回归模型,没有出现明显的偏离现象,预测性能较为稳定。其次,峰值的捕捉能力,对于高峰现的捕捉,可以看到1964年和1984年的9月份与1964年的10月份,GWO-BP比GWO-LSTM和逐步回归模型预测的结果更接近于观测值,对洪峰有更好的反应能力,但GWO-BP和GWO-LSTM两者差值不大;对于低峰现的捕捉,3种模型的能力基本等同,GWO-BP略有优势,但在1994年的9月份和1990年的10月份,预测出现异常,表现出明显的低估现象,可能是其简单的网络结构所引起,对高峰现的过度拟合导致后面的低估现象。

图4 各模型训练期对比结果Fig. 4 Training periods results of various models
综上所述,在同等条件下,GWO-LSTM模型无论在预测精度还是泛化能力上都要优于GWO-BP模型更优于逐步回归模型,虽然在峰值的捕捉能力上略有不足,但没有出现较大的偏差现象。同时对比于近年来关于丹江口水库月入库径流的预测情况,与以机器学习算法进行的丹江口水库月入库径流预测[22]相比,GWO-LSTM模型的预测效果有较大改善。与以物理模型进行的丹江口水库月入库径流预测[23]相比,GWO-LSTM模型稍有不足,但相差不大,而且相对于物理模型前期输入资料的收集难度,机器学习模型的输入资料收集更加容易,资料较为完整。
另外,丹江口水库于1973年建成,其前后的产汇流特性发生较大变化。对比了1973年前后其预测精度的变化,1973年前后3种模型的纳什效率系数及均方根误差都发生了变化,1973年前其纳什效率系数平均高于1973年后7%,均方根误差平均低于1973年后4亿m3,1973年前的预测精度整体好于1973年后,说明水库建成前后流域的产汇流特性变化对机器学习方法的预测有影响,其具体变化原因需要进一步分析。但总体上GWO-LSTM模型对丹江口水库月入库径流的预测效果较好。
4.2 模型优化分析
对GWO算法进行验证,以神经元个数和学习率为例,其结果如图5~6。可以看到在神经元个数[3,50]范围内,GWO确实可以找到全局的最优点(38,17.251),而且在第4次迭代就趋于收敛。同理在学习率中也找到最优点(0.033,12.224),在第2次迭代就趋于收敛,说明了GWO具有全局遍历和收敛较快的优点。
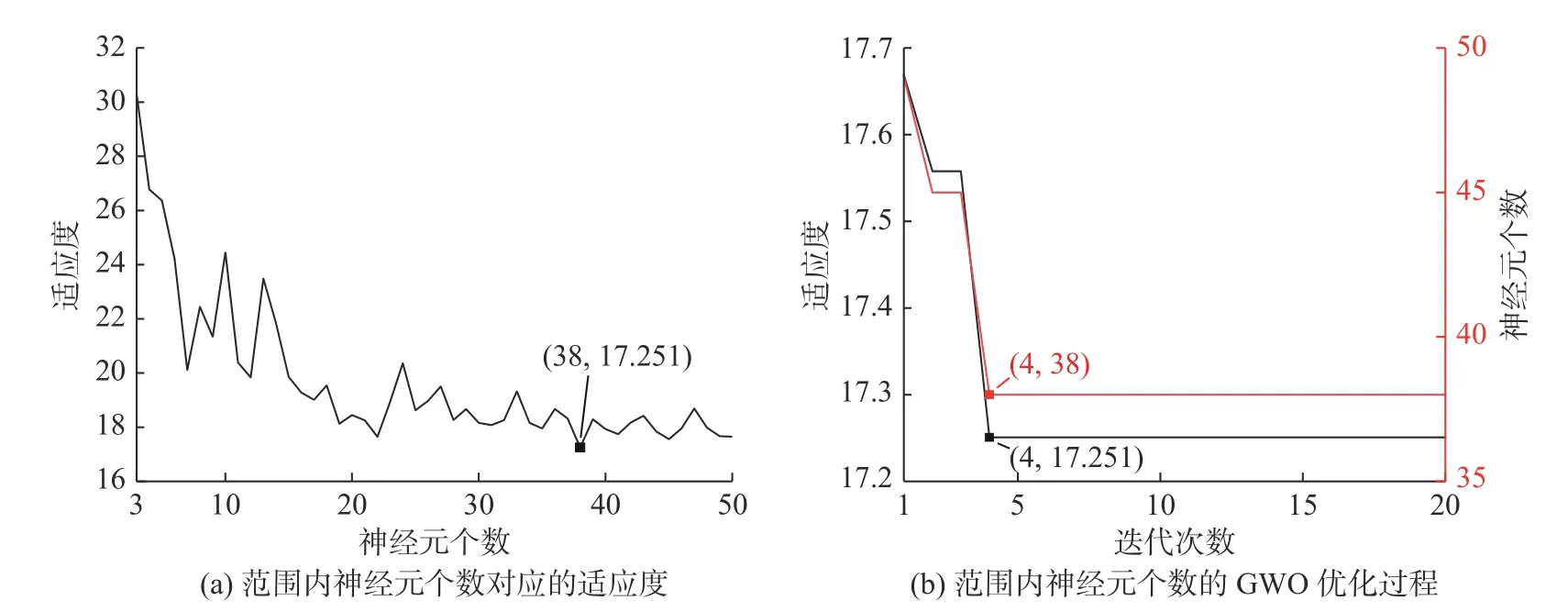
图5 神经元个数优化过程Fig. 5 Optimization process of neuron number

图6 学习率优化过程Fig. 6 Optimization process of learning rate
然后将GWO算法应用于LSTM神经元个数、初始权重、阈值的优化上,训练期和验证期效果见图7。可见,人工调参的预测效果不如GWO优化,经过GWO优化其训练期的ERMS和ENS分别为8.126亿m3和0.952,验证期为4.292亿m3和0.985,人工调参训练期的ERMS和ENS分别为15.045亿m3和0.837,验证期为25.171亿m3和0.472,可以看到人工调参的LSTM模型其验证期的ENS不足0.5,未达到可接受范围。说明GWO和LSTM结合提高了预测精度,也减少了时间成本,平均在3次后就可以达到收敛状态。但也存在不足之处,对于GWO其全局最优性目前并没有较为科学严谨的证明,仍然存在争议;而且LSTM参数较多,优化过程耗时较长,对实时性水文预测的能力较弱,因此可进一步考虑将其与一些并行方法相结合。

图7 GWO-LSTM和LSTM的模拟效果对比Fig. 7 Comparison of the simulation effects of GWO-LSTM and LSTM
5 结 语
基于GWO-LSTM开展丹江口水库月入库径流的预测研究,对比不同模型在GWO优化下的预测效果。结果表明:GWO-LSTM模型在预测精度和泛化能力上明显优于GWO-BP模型和逐步回归模型,虽然在峰值捕捉上略有不足,但整体预测效果较好,其纳什效率系数平均在0.95以上;在网络结构超参数的选择上,超参数依据经验取值其预测结果不如GWO优化,依据经验取值其验证期的纳什效率系数不足0.5,未达到可接受范围,而且具有一定的偶然性,为了避免局部最优情况,建议选用带有全局优化特点的算法进行超参数取值;验证了GWO算法具有全局遍历性和收敛快的特点。

