基于VMD-WOA-LSSVM 的汽轮机轴承振动趋势预测

李劲松，张 双，董 泽，王泽轩，罗代强

（1.河北国华定州发电有限责任公司，河北 定州 073000；2.华北电力大学河北省发电过程仿真与优化控制技术创新中心，河北 保定 071003；3.贵州黔西中水发电有限公司，贵州 黔西 551500）

0 引言

汽轮机组是电厂中的大型旋转机械，其运行的稳定性关乎生产过程的安全。汽轮机轴承分别在轴向和径向发挥不同的作用，在轴向，轴承承受转子转动的轴向推力，并为动静叶之间保留适当的轴向间隙；在径向，轴承起到承担转子负荷和在转子转动过程中产生的离心力的作用。当汽轮机发生油膜振荡，转子热变形，气流激振等故障时，都会产生轴承振动幅值异常的现象［1-2］。因此，若能及时预测出轴承振动的异常状态，提前预警汽轮机故障趋势，进行预防性监测，对加强汽轮机组的安全管理尤为重要。

基于物理模型的预测方法是依据物理学等方法得到高精度的物理模型，进而对物理模型进行模拟、计算与评估［3］。但该方法预测精度依赖于模型精度，物理模型精度提高不易实现，计算复杂。基于统计学的预测方法是通过找到输入数据和预测值之间的映射关系，挖掘数据潜在的规律［4］，构建预测模型。ARIMA 等传统方法和SVM、ELM、LSTM 等机器学习方法已在各领域的时间序列预测中得到了广泛应用［5-7］。其中，ARIMA 方法适用于预测变化平缓的线性序列，对变化快速的信号预测精度较低。机器学习方法则在非线性序列的预测方面占有优势［8］。

由于汽轮机轴承处于较为复杂的环境中，采集到的信号是非稳定的、非线性的，而且含有较强的噪声，因此，数据处理对故障预测的准确性具有重要影响。剡昌锋等［9］采用形态滤波器对汽轮机转子振动监测数据预处理，再利用EEMD 方法分解出一系列分量，对各分量建立ARIMA 预测模型，预测振动信号的变化趋势。田宏伟等［10］采用CEEMDAN 将风机的振动信号分解成一系列固态模量，使用鲸鱼算法优化的极限学习机来预测所有分量，最后将各个分量预测结果相叠加得到最终预测值，提高了风机振动的预测精度。小波变换、EMD、EEMD 和LMD 等分解方法已在时间序列预测中提高了预测精度，取得了更好的效果［11-13］。然而，EMD 和LMD 二者基于递归方法对信号进行分解，可能会造成端点效应、误差较大等问题［14］。变分模态分解（Variational Mode Decomposition，VMD）是基于变分法，能够将模态更好地分离，具有更优的噪声鲁棒性，更适用于振动信号的分解，其效果已在多个领域得到了验证［15-16］。

本文基于变分模态分解方法分解轴承振动的时间序列，从而对振动信号降噪，同时保留原始信号中的有用成分。然后采用鲸鱼算法（Whale Optimization Algorithm，WOA）与最小二乘支持向量机（Least Squares Support Vector Machine Classifiers，LSSVM）组成的WOA-LSSVM 模型对分解的每一个子序列进行预测，WOA 对核函数参数和惩罚因子进行优化，获得最优的模型参数，提高预测精度，最后将预测结果相叠加得到最终的预测值。

1 研究方法

1.1 变分模态分解

变分模态分解是K.Dragomiretskiy 和D.Zosso 首先提出的。EMD 分解方法采用循环筛选的方式，而VMD 方法采用迭代搜寻变分模型的最优解的方式，最后将信号分解成K个具有不同中心频率的限带本征模态函数［17］。

VMD 分解主要包括变分问题及其求解，主要包括希尔伯特变换、频率混合和经典Winner 滤波3 个部分［18］，具体步骤如下。

1）分别对各个模态函数的解析信号进行希尔伯特变换。

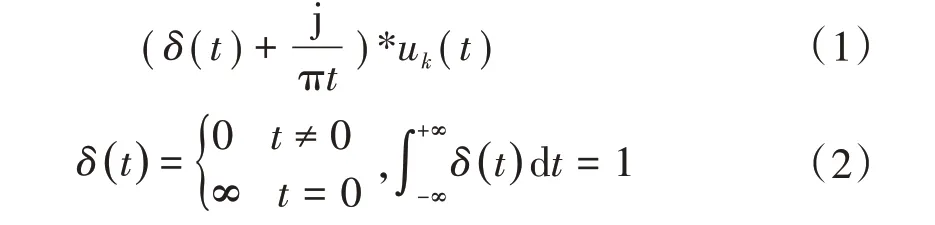
式中：uk(t)为模态函数；δ(t)为狄拉克函数；*表示卷积。

2）加入各模态中心频率ωk的指数项，由频谱得到基带信号

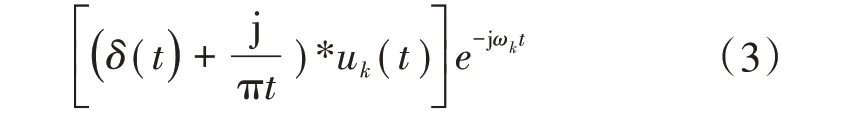
3）计算uk(t)的带宽，对变换得到的信号基于高斯平滑法进行估计，这样此问题求解可转换为带约束的变分问题。

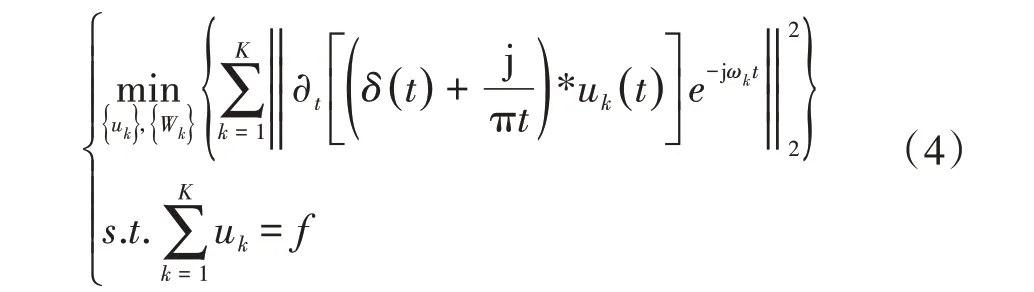
式中：{uk}={u1，…，uK}为各模态函数；{ωk}={ω1，…，ωK} 表示各函数的中心频率；K为要分解的模态数；f为原始输入信号。

对该变分问题的求解，引入增广拉格朗日乘子得到非约束性变分问题。式中：α为惩罚因子，λ为拉格朗日乘子。

中心频率的计算结果为

1.2 WOA-LSSVM 模型

1.2.1 WOA算法

鲸鱼优化算法是Seyedali 等在2016 年提出的一种优化算法，来源于群居哺乳动物座头鲸在捕食时相互合作捕获猎物的过程［19］。在该算法中，可行解由座头鲸的位置表示。鲸鱼有两种捕食方式，一种是所有鲸鱼包围猎物，向着某一只的鲸鱼前进，鲸鱼将会随机选择是向着最优位置的鲸鱼还是任意一只鲸鱼游去；另一种是通过上升螺旋气泡网将猎物捕获。鲸鱼群体会于上述两种捕猎方式中进行随机选择。鲸鱼优化算法主要包括3 个阶段，分别为包围捕食、气泡网袭击和猎物搜索。

WOA算法的步骤如下。

1）包围捕食。

座头鲸可以分辨猎物位置并包围猎物。由于最优设计在搜索速度中位置未知，WOA 算法将目标猎物作为当前的最佳候选解，并由此进行位置更新。这一行为的表示方法为：

式中，A和C是随机系数向量；X*是目前最佳解的位置向量；X为位置向量；t为迭代次数；X(t+1)表示下一次迭代后的位置向量；D为包围步长。如果能搜索到更好的解，则在每次迭代中更新X*。

其中向量A和C的计算方式为：

在整个搜寻过程中，参数a由2 线性降到0；r1和r2为[0，1 ]之间的随机向量。

2）气泡网袭击方式。

收缩包围：鲸鱼更新后的新位置可为目前位置与最佳鲸鱼个体位置之间，由式（8）更新确定。

上升螺旋式：鲸鱼与猎物间距离D′根据式（11）计算确定。

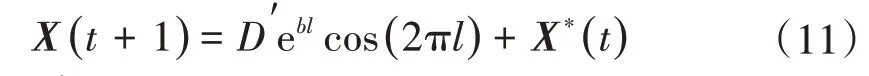
式中：D′=|X*(t)-X(t)|为目前搜索得到的最佳解；b为常数，用来定义螺旋线的形状，l为［-1，1］的随机数。

座头鲸在捕获猎物时，绕着逐渐缩小的包围猎物的圆圈游动，同时沿着上升的螺旋形状的线路游动。为了将这两种同时发生的行为更加精准地模拟出来，假设鲸鱼发生缩小的包围机制和螺旋模型两种行为的概率相同，各为50%，构建式（12）来更新鲸鱼的位置。

式中：p是0到1之间的随机数。

3）猎物搜索。

当 ||A＞1 时，算法会随机地搜索鲸鱼进行位置的更新，并不是将目前的最佳搜索位置作为最优位置。这种机制和 ||A＞1 强调探索，当达到最大迭代次数后终止算法。

1.2.2 LSSVM模型

最小二乘支持向量机方法能够将非线性的输入样本映射到高维的特征空间，将非线性方程组转换为高维的线性方程组的求解问题，是一种SVM 在二次损失函数下的形式，简单快捷，计算资源需求小，适用于回归预测问题的解决。

LSSVM的回归模型可表示为

式中：ω为特征空间权系数向量；b为偏置。将LSSVM的回归模型转换为约束优化问题

式中：C为惩罚因子；ei为误差变量。

引入拉格朗日函数，将该优化问题变换到对偶空间，则

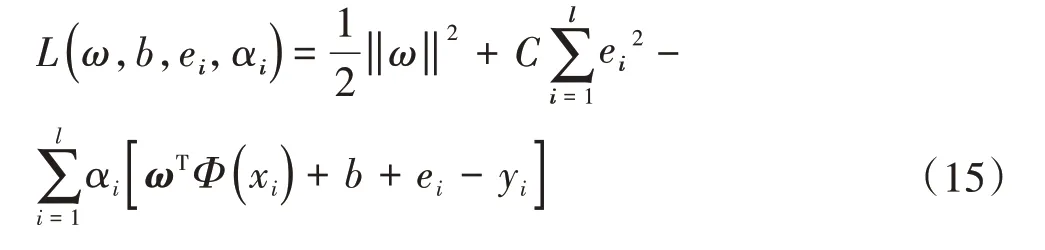
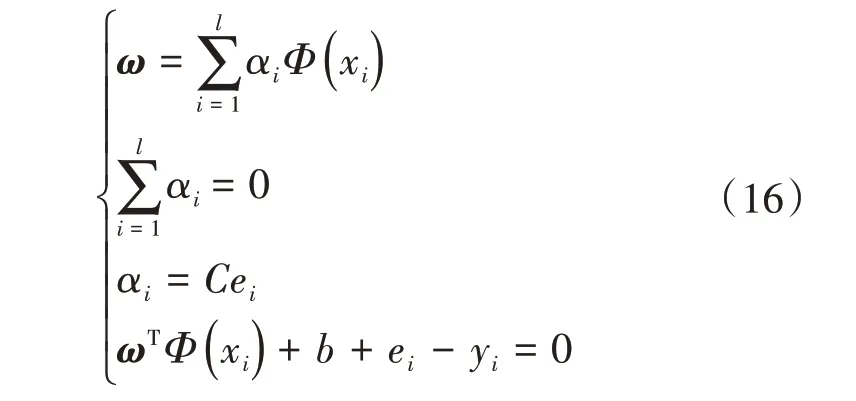
消去ω和ei，可得到如下线性方程组：

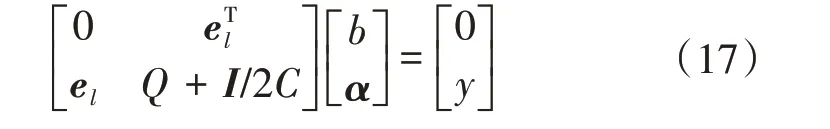
式中：el为l维单位列向量；I为单位矩阵；α=[α1，α2，…，αl]T；Qij=K(xi，xj)，其中，i，j=1，2，…，l。

最终得到回归函数为

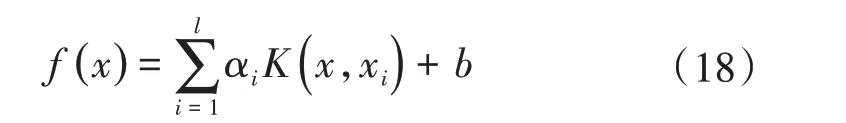
式中：K(x，xi)=Φ(x)Φ(xi)为满足Mercer 条件的核函数。

核函数采用径向基函数为

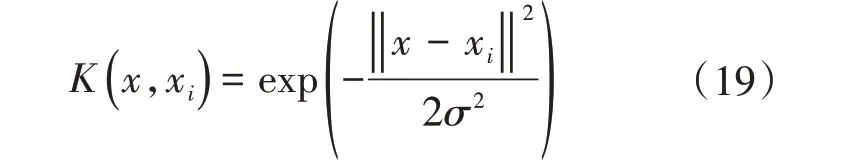
式中：σ为核函数参数。

1.3 优化预测模型

汽轮机振动数据具有非线性和非平稳性的特点，若直接采用传统的时间序列预测方法，预测精度不高。为此，采用变分模态分解方法，先将振动信号分解，再对振动序列分解成的一系列分量分别使用LSSVM模型进行预测，再将各分量的预测结果集成，得到最终的预测结果。

整个优化预测的模型步骤如图1 所示。在径向基函数为核函数的LSSVM 预测模型中，惩罚因子C和核函数参数σ是影响预测精度的主要参数，C影响训练误差及泛化能力；σ决定了局部邻域的宽度。采用WOA算法对这两个参数进行优化。

4月19日，来华访问的泰国总理英拉到访水利部，并与国家防汛抗旱总指挥部副总指挥、水利部部长陈雷进行会谈。双方就水资源管理、水利防灾减灾和深化两国水利领域交流合作深入交换了意见。泰国外交部部长素拉蓬·都威乍猜军，国务部部长娜丽妮·塔维信、尼瓦塔隆·汶松派汕，科技部部长包巴索·苏拉瓦蒂，泰国驻华大使伟文·丘氏君，总理顾问素春·差里科，总理副秘书长尼鲁·坤那瓦，外交部副次长诺帕敦·坤威汶，中国水利部党组成员、中纪委驻部纪检组组长董力，水利部副部长周英、胡四一、李国英，中国驻泰国大使管木等参加会谈。

图1 优化模型流程

2 仿真实例

2.1 数据获取

采用江苏某电厂汽轮机1 号轴承的监测数据进行研究。选取2016 年6 月23 日至6 月24 日的振动监测数据，采样的时间间隔为1 s。为研究需要，将其每分钟平均化处理，并取2 000 个。在该段时间序列数据中，取前1 400 个数据为训练数据，后600 个数据为测试数据。

振动数据的时间序列如图2所示。

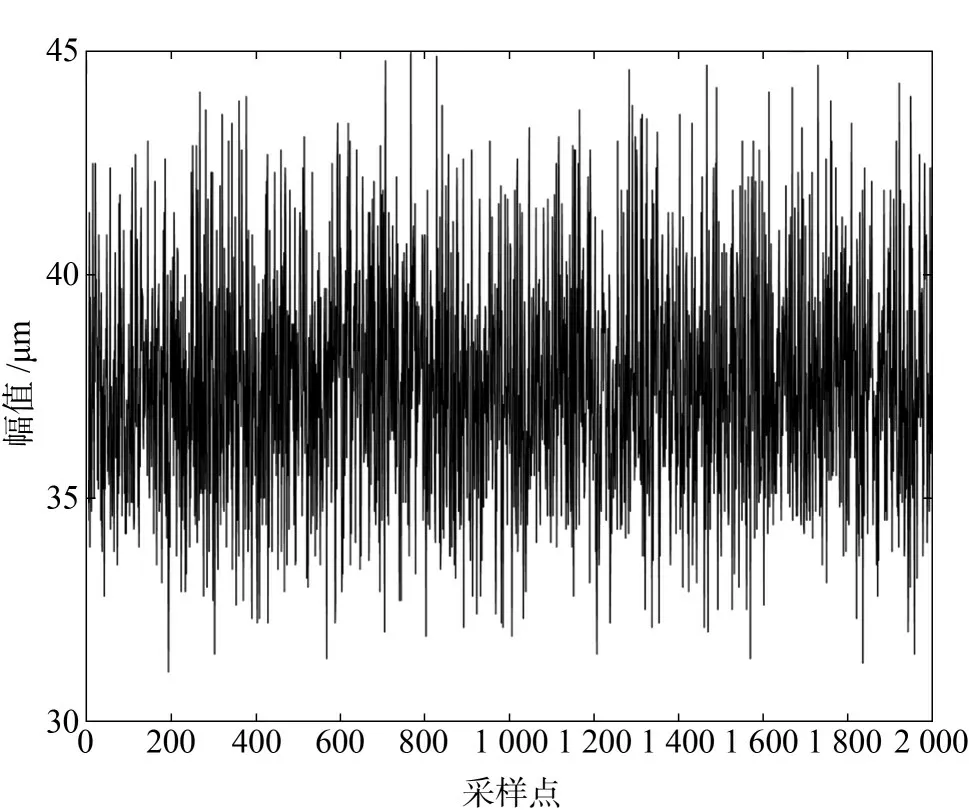
图2 振动数据

2.2 VMD分解

基于VMD 方法分解的模态数对分解效果有很大影响，如果K值选择过大或过小，会导致过度分解或分解不足。本文根据各模态中心频率方法确定K值。在VMD分解中，参数α为2000，τ为0.3。

通过表1分解结果可知，K=4时，模态分解不足，当K=6时，模态中出现中心频率为3 714 Hz和3 907 Hz两个很相近的模态，可认为此时已将振动信号过度分解，因此，模态数选为5。分解结果如图3所示。

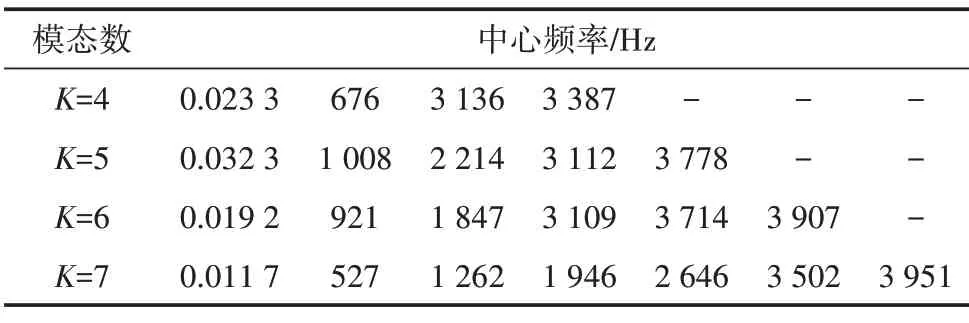
表1 不同K值对应的中心频率

图3 VMD分解结果

2.3 预测模型构建

分解后需要对子序列分别进行归一化以提高运算速度，采用的归一化方法为

在WOA-LSSVM 预测模型中，本文选取的适应度函数为均方误差，其表达式为

式中：fMSE为适应度值；n为样本个数；xi为实际值；为预测值。

设定鲸鱼种群个数为50，最大迭代次数为30。

具体建模过程如下：

1）读取数据样本，对数据进行预处理；

2）初始化鲸群位置，利用鲸鱼算法和训练集数据对LSSVM进行训练，计算适应度值，保存最佳位置；

3）随机产生p值，根据p值和 ||A的大小来选择位置更新的方式为收缩包围机制、气泡网袭击或者猎物搜索；

4）在满足迭代条件之前，一直重复步骤2）-3）。

5）根据以上步骤确定的惩罚因子C和核函数参数σ对每个子序列建立WOA-LSSVM 模型，利用建立的预测模型在测试集上进行预测。

6）最终预测结果为所有子序列预测值的和。

2.4 误差指标

选取平均绝对误差（EMA）、平均相对误差（EMAP）、误差均方根（ERMS）用于评价振动信号在VMD 分解后的准确度的指标，如式（22）—式（24）所示。

其中，xi为实际值，为预测值。

3 仿真实验

为了验证所提出预测模型的有效性，选取WOALSSVM 模型与VMD-PSO-LSSVM 模型与VMD-WOALSSVM 模型进行对比试验。不同预测模型的预测效果如表2所示。

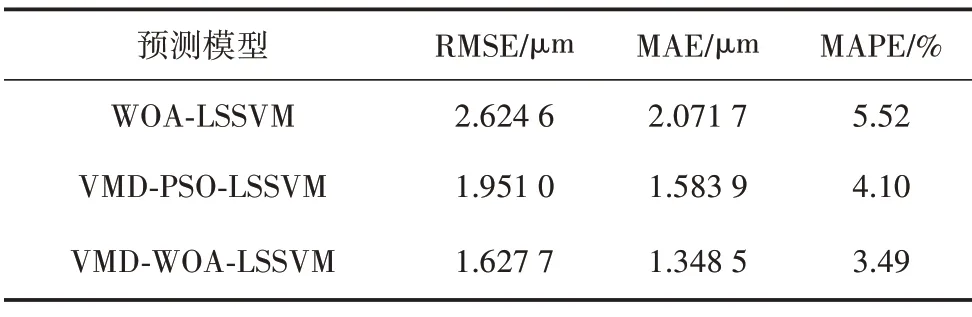
表2 不同模型的预测误差

从表2 中预测误差可以分析出，经过VMD 分解后，预测模型精度较未分解的预测模型精度均有提高，其中，VMD-WOA-LSSVM 模型比VMD-PSOLSSVM 的预测精度有一定的提高，说明WOA算法的全局寻优能力优于PSO 算法，更适用于优化振动序列。较其他两种对比模型，提出VMD-WOA-LSSVM的模型在预测误差指标中，ERMS分别降低了37.98%，16.57%，EMA分别降低了34.9%，14.86%，EMAP降低了36.78%，14.88%。

图4 为各模型预测结果曲线和实际值的对比图及截取的部分预测细节图像。

图5 为各个模型在每个预测点上的相对误差δ（t）所构成的图像。

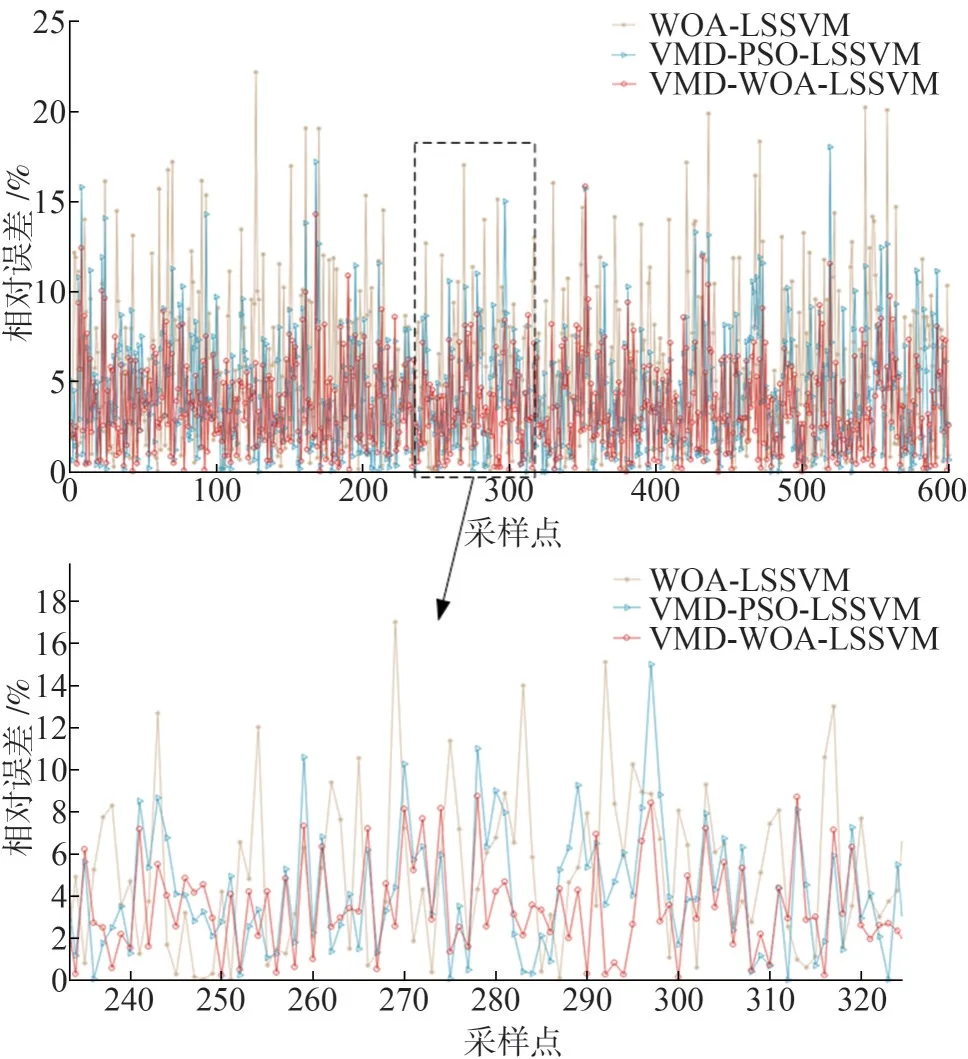
图5 3种预测模型相对误差

由图4 可见，所提出的VMD-WOA-LSSVM 模型与实际值的变化趋势最为符合，预测精度最高。

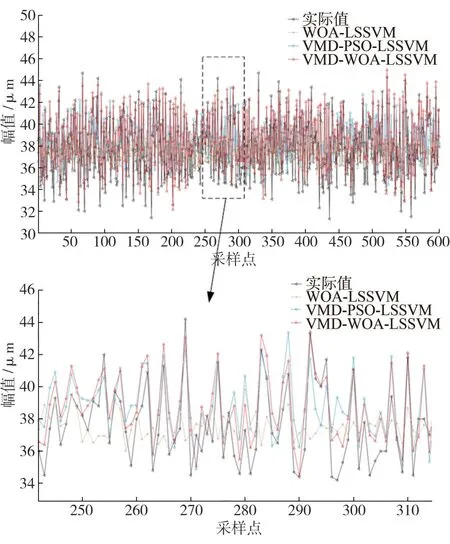
图4 3种模型预测结果

从图5 中可以看出，VMD-WOA-LSSVM 模型的大部分预测点误差都较小。

相对误差百分比统计情况如表3 所示。可以看出，VMD-WOA-LSSVM 模型预测结果中预测点大部分相对误差小于5%，只有一个点的相对误差大于15%。相较WOA-LSSVM 和VMD-PSO-LSSVM 模型，VMD-WOA-LSSVM预测模型相对误差大于15%的采样点的个数分别下降了95%和79.5%，预测结果较为理想。

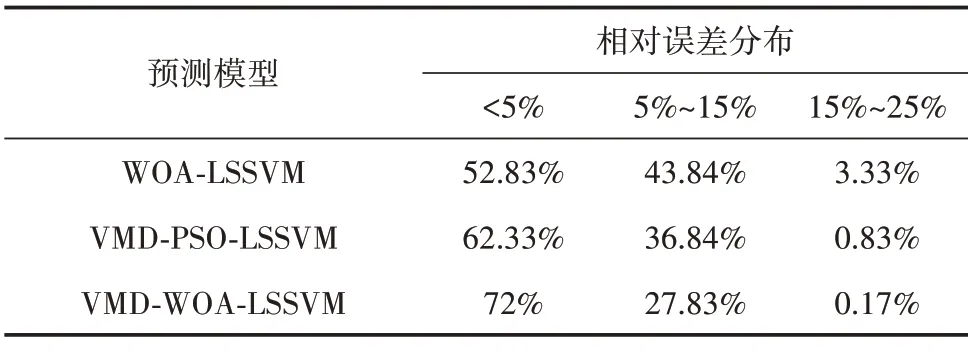
表3 相对误差分布

4 结论

提出一种VMD-WOA-LSSVM 模型用于汽轮机轴承振动趋势预测，利用某火电厂的轴承振动序列来验证该模型的预测精度。利用VMD 方法分解振动序列为具有不同中心频率的子序列，建立WOA 算法优化的LSSVM 预测模型，以WOA-LSSVM 与VMDWOA-LSSVM模型的预测效果作为对比实验，均方根误差分别降低了37.98%和16.57%。分析实验结果得到以下结论：

1）变分模态分解能够降低振动信号的非线性和非稳定性，利用此方法将信号分解再集成可提高模型预测精度；WOA 算法的全局搜索能力较强，可得到更好的优化效果，降低预测误差；

2）VMD-WOA-LSSVM 模型预测精度高，可将此方法改进并应用于同类型信号快速变化的非线性序列的预测。

提出的VMD-WOA-LSSVM 预测模型适用于振动趋势预测，及时预测出轴承振动的异常状态，可为汽轮机故障预警提供科学依据，对汽轮机组的安全稳定运行具有重要意义。