QML:一种混合空间索引结构
崔栋,温巧燕,张华,王华伟
(北京邮电大学网络与交换技术国家重点实验室,北京 100876)
1 引言
物联网设备会生成大量的地理空间数据,为了有效地访问和处理此类数据,数据库管理员通常会采用基于树的索引结构来提高数据分析和事务性工作负载性能[1]。为了提升数据库的读写性能,整个索引通常会保存在内存中。但当数据量达到PB级别以上时,树形索引结构会急速变大,进而严重侵占系统资源。研究表明,在商用内存数据库中,索引占用了全部内存空间的55%[2]。现有的索引结构在空间大数据环境下面临存储空间占用高和查询I/O 次数多的问题。
机器学习算法的引入从根本上改变索引结构。2018 年,Kraska 等[1]在SIGMOD 会议上首次提出了学习索引的概念。他们将机器学习方法应用于索引结构中,在降低索引空间代价的同时提升了索引查询性能。紧随其后,学者从一维数据结构和多维数据结构中开展了研究工作。其中,一维索引的研究主要有FITing-Tree[3]、AlEX[4]、PGM-index[5]、XIndex[6]、Dabble[7]等,多维索引的研究主要有ZM 索引[8]、ML-Index 索引[9]、LISA索引[10]和Flood 索引[11]等。空间数据库主要使用的是多维索引。
2019 年,Wang 等[8]在多维空间数据上使用Z顺序曲线进行投影降维构建了支持范围查询的ZM索引。ZM 索引不支持K近邻(KNN,K-nearest neighbor)查询,也不支持插入和删除操作。2020 年,Davitkova 等[9]为了支持KNN 查询,基于iDistance方法构建了ML-Index 索引,但是没有解决插入和删除的问题。同年,Li 等[10]和Nathan 等[11]在SIGMOD 会议上分别提出了LISA 索引和Flood 索引。LISA 索引支持了索引的插入和删除操作,在一定程度上优化了效率,但是LISA 索引并不适用于频繁大规模更新的空间数据集。Flood 索引相比于之前的索引大幅度优化了存储,提高了查询性能,但是只支持只读工作负载,不支持插入等操作。
本文使用四叉树索引结构对空间数据进行均匀快速的划分,使用Z顺序曲线进行数据降维。为了使生成的QML 索引更符合数据的分布特征以支持快速的更新和查询操作,本文提出了动态数据分段算法DDSA。该算法生成的数据段符合线性和二次曲线分布,这2 种分布更接近现实数据情况。本文在此基础上使用分段线性函数和二阶多项式函数拟合多维空间数据构建QML 索引,并实现了范围查询和KNN 查询。实验结果表明QML 索引存储比R*-tree[12]等减少33%,更新效率提升40%~80%,查询效率与最优树形索引相近。QML 索引数据更新的时间复杂度仅为O(1),优于LISA 索引。本文的主要贡献如下。
1) 提出了QML,这是一种新的混合空间索引结构,在保证索引查询和更新性能的同时,降低存储空间,是利用数据分布规律来构建空间索引的一种新的尝试。
2) 提出了适用于学习索引的动态数据分段算法DDSA,该算法能够根据局部数据分布特征选取不同的多项式函数进行拟合。
3) 设计并实现了基于QML 的范围查询算法和KNN 查询算法,并通过真实数据集的测试证明QML 提供了与最优树形索引结构相近的(点查询性能更好)查询性能和更新性能,大幅降低了存储空间。
2 相关工作
空间索引是为多维数据访问设计的数据结构。大多数空间索引是空间驱动或数据驱动的结构[13]。空间驱动的结构(如固定网格索引[14])将空间分解为单元格,并根据几何准则映射数据对象。数据驱动的结构(如R-tree[15])将数据对象划分为簇,并通过其最小外接矩形(MBR,minimum bounding rectangle)划分空间。此外,UB-tree[16]是Z顺序曲线[17]和B+tree 的组合,是一个平衡树,数据对象按Z阶存储。实际数据具有一定的分布特点,但是传统的数据索引结构没有利用这一特点,因此不能发挥数据最大的作用。
由文献[18-22]可知,学习索引可以充分利用数据的分布规律,在提升查询性能的同时降低空间消耗。ZM 索引[8]使用Z顺序曲线进行降维;ML-Index索引[9]采用基于iDistance[23]方法的改进策略对数据进行投影;LISA 索引[10]使用网格划分和基于勒贝格测度的投影进行数据有序化。Flood 索引[11]采用基于成本模型的网格划分策略;在模型选择上,ZM索引和ML-Index 索引都选用了RMI 模型;为了使索引拥有更低的空间成本和执行成本,LISA 索引和Flood 索引选择使用分段线性回归模型。在空间查询应用中,已有的多维索引都实现了对空间范围查询的支持,ML-Index、LISA 索引和Flood 索引还可以支持KNN 查询。Nathan 等[11]没有给出利用Flood 索引进行KNN 查询的具体实现。LISA 索引采用格子回归模型[24],并结合范围查询实现了KNN 查询。
支持频繁的数据更新是上述多维学习索引面临的一个难题。ZM 索引、ML-Index 索引和Flood索引目前仅支持只读的静态负载;LISA 索引虽然通过采用异地插入的方式支持了索引插入和删除,但是索引的更新效率随着数据更新规模的增加而下降,因此不适用于频繁更新的空间数据。为了应对可能频繁更新的空间数据,本文提出了QML 混合空间索引结构。QML 索引在支持范围查询和KNN 查询的基础上,通过动态数据分段算法DDSA快速构建本地模型,在大幅降低存储空间和提高动态更新效率的同时,获得近似最优树形空间索引的查询性能。
多维空间数据在降维和有序化后可以近似看作具有时序特征的数据。时序数据的分段模式表示是一种对时序数据进行抽象和概况的表示方法[25]。分段线性近似(PLA,piecewise linear approximation)算法将数据分割成若干段后使用线性函数来逼近每个段。Liu 等[26]提出了一种利用PLA 实现紧凑分段的方法,称为可行空间窗(FSW,feasible space window)。FSW 算法通过可行空间的概念,在保证每个数据点有误差界的情况下,可以找到每个数据段的最远分割点,在学习索引模型FITing-Tree[3]中应用的就是该方法。但FSW 算法无法直接用于非线性函数。Xu 等[27]在此基础上提出一种可行系数空间(FCS,feasible coefficient space)算法用于解决该问题。该算法通过寻找特定函数系数边界确定一个可行系数空间,通过不断缩小该空间的范围来进行数据分段。FCS 算法适用于各种复杂多项式函数的拟合,但空间数据一般呈二次曲线分布,FCS 算法对于索引构建过于复杂。
本文针对上述的问题提出了适用于学习索引的动态数据分段算法DDSA,该算法使用分段线性函数和二阶多项式函数进行分段,在保证分段效率的同时尽可能将相似数据划分到一起。
3 QML 索引
3.1 QML 核心思想
本文选取了公开数据集OpenStreetMap[28]上的美国本土各类建筑、商店等标签的地理信息,通过Z顺序曲线变换后数据的分布规律如图1 所示。从图1 中可以看出,空间数据在经过降维和序列化后呈单调递增的分布规律。
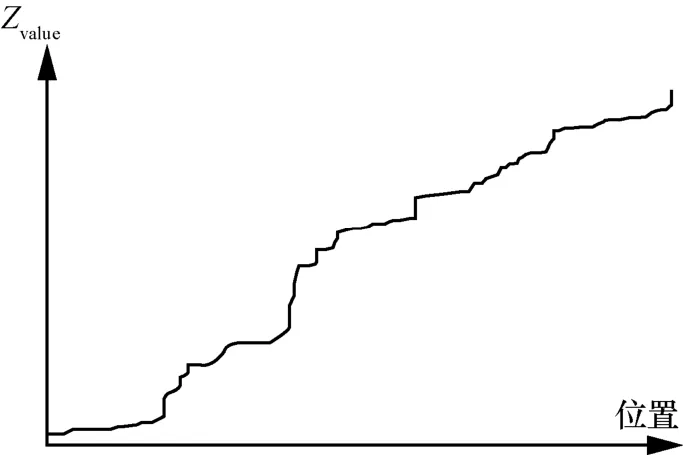
图1 OSM 美国本土地理信息数据分布规律
为了更好地拟合数据分布并支持索引的动态更新,QML 索引采用四叉树进行数据划分,Z顺序曲线进行数据降维和有序化,最后使用动态数据分段算法DDSA 进行数据分段和模型构建。
四叉树的生成和维护比较简单,当数据分布比较均匀时,有较高的数据插入和查询速率。当数据分布不均且数据量较大时,为了缓解数据偏移带来的索引树不平衡的压力,QML 索引使用存储最大数据量阈值的单元格cell 作为四叉树的叶节点,减少中间节点的数量和树深度。LISA 索引采用的网格划分策略因为在数据变动较大时需要重新排序并划分,所以并不适用于频繁变更的数据集,相比之下,QML 的四叉树结构则可以更灵活快速地进行索引插入和删除操作。
在存储优化方面,QML 索引的节点包括中间节点和叶节点,中间节点不存储数据,叶节点存储最大数据量阈值的数据和本地模型集合。因此QML可以显著降低中间节点的数量,减少存储消耗。
在索引动态更新方面,四叉树的数据分割策略将数据空间V按数据量划分成最小单元格cell,保证在数据更新时只需对单独cell 上的模型进行重构,避免相互间的影响。动态数据分段算法DDSA 可以通过一次性的数据遍历构建索引模型。实验表明QML 索引拥有比传统索引更好的更新性能。
在查询性能优化方面,QML 的混合索引结构通过减少中间节点减少了不必要的间接查询,其模型可以根据数据分布特征选取不同的多项式函数进行拟合,减少不必要的数据分段。这些结构设计可以优化QML 索引查询算法,提高检索速度,同时也很好地支持了范围查询和KNN 查询。
3.2 QML 构建
如图2 所示,QML 索引的构建过程可以分为3 个阶段:数据划分、数据降维和有序化、数据分段和模型生成。相关参数定义如表1 所示。QML 索引的输入为原始数据集Data:Data={ki|i=0,1,…,t}。

图2 QML 构建示意

表1 参数定义
阶段1数据划分
步骤1将原始数据集Data 的数据点ki映射到二维数据空间V=[0,X)[0,Y)∈R2,计算数据空间V的数据量Vcount;
步骤2如果Vcount>Cell_max_count,执行步骤3;如果Vcount≤Cell_max_count 则构建单元格cell,将cell 加入根节点并执行阶段2 的步骤4;
步骤3对数据空间V按照四叉树进行等距划分,生成4 个子数据空间{NW,NE,SW,SE}并加入根节点中,对新生成的空间区域Vi∈{NW,NE,SW,SE}利用步骤1 再次进行划分;
(见算法1 的第1)行~第11)行)
阶段2数据降维和有序化
步骤4对于单元格 cell 内任意的ki=(xi,yi)按照Z顺序曲线映射函数M计算,构建三元组
步骤5对单元格cell所有的按照由小到大排序,形成有序数据集
(见算法1 的第12)行~第21)行)
阶段3数据分段和模型生成
步骤6将有序数据集d中每个的和j映射到二维空间,然后使用DDSA 进行数据分段,得到数据集合D={di | i=0,1,…,m};
步骤7根据每个子数据集di的数据分布特征分别使用线性函数和二阶多项式函数进行拟合,生成本地模型集合L={li|i=0,1,…,m};
(见算法1 的第22)行~第24)行)


4 动态数据分段算法DDSA
为了使索引的模型更加符合数据分布特征并提高构建效率,本文设计的动态数据分段算法DDSA采用FSW算法[27]和SFCS算法交叉验证的方式,分别使用线性函数和二阶多项式函数进行拟合。其中SFCS 算法是本文针对数据的非线性特征专门设计的一个与之适配的简化可行系数空间算法。
本文DDSA 的工作原理是将待分割有序数据集的第一个数据点初始化为分段的左端点,然后在每一步中尝试将下一个点也放入分段。新加入的数据点需要在当前分段的最大误差允许范围内,如果超过最大误差则开启新的分段。其关键是使当前分段在给定的最大误差下尽可能地延长。
对于每一个分段,DDSA 都会根据最大误差阈值生成一个可行区间S。当有新的数据点加入时,算法需要结合初始点和最大误差阈值计算新数据点的可行区间S′,当2 个区间S和S′没有共同区域时则表示当前分段结束。
DDSA 先使用FSW 算法[27]判断新加入的数据点是否符合线性分布,如果不符合再使用本文设计的SFCS 算法判断是否为二次曲线分布。
DDSA 的详情如算法2 所示。DDSA 输入为有序数据集data、最大误差阈值ε和算法类型type。算法类型type 分别用0 和1 表示FSW 算法和SFCS算法。输出结果为数据集Data 的本地模型集合L。

首先进行初始化操作。设置type=0,构建FSW算法可行区间Sfsw,初始数据段d包含第一个和第二个数据点,初始数据点设置初始数据段d的算法类型d.type=0。
算法从数据点开始遍历。用FSW 算法构建新的可行区间Sfsw,当该可行区间为空时改用SFCS算法进行判断。每一次从FSW 算法切换到SFCS算法时都需要进行初始化操作,选取当前数据段的起始点、中间点和最后数据点构建SFCS 算法的可行区间Ssfcs。然后根据新生成的可行区间Ssfcs来判断待检测点是否满足二次曲线分布。
如果在处Sfsw和Ssfcs都为空,则在此处进行切分,作为下一个数据段的起始点。d形成新的数据段。最后根据d的算法类型d.type 确定使用线性函数或者二次多项式函数进行拟合生成本地模型l,加入模型集合L中。
上述过程中,SFCS 算法通过计算二次多项式函数参数的可行区间进行判断。详情如下。
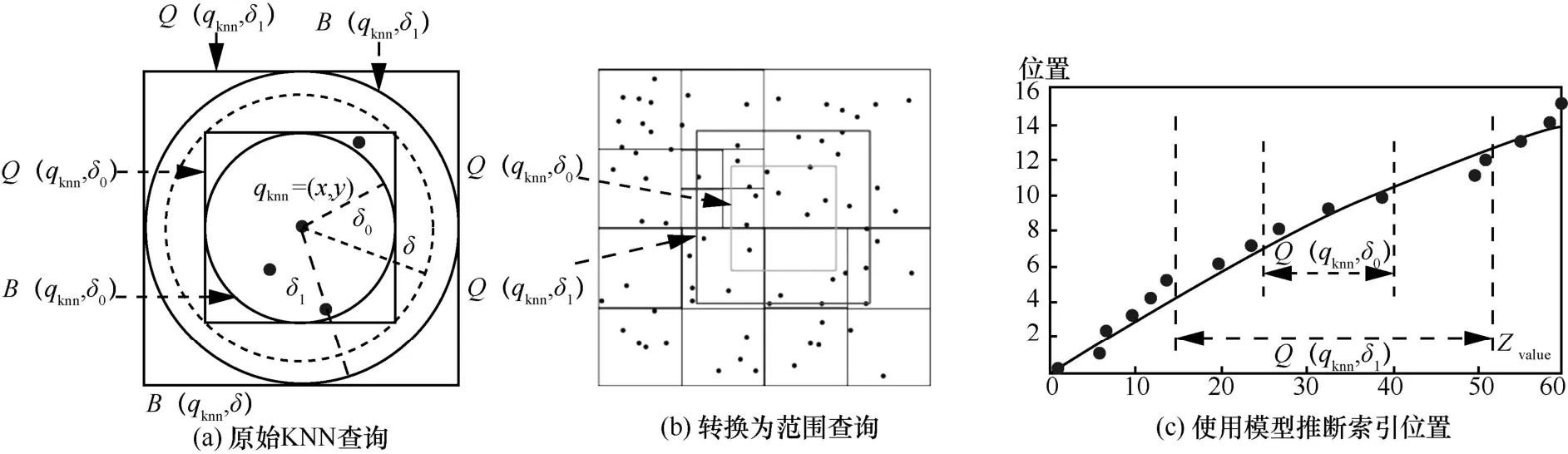
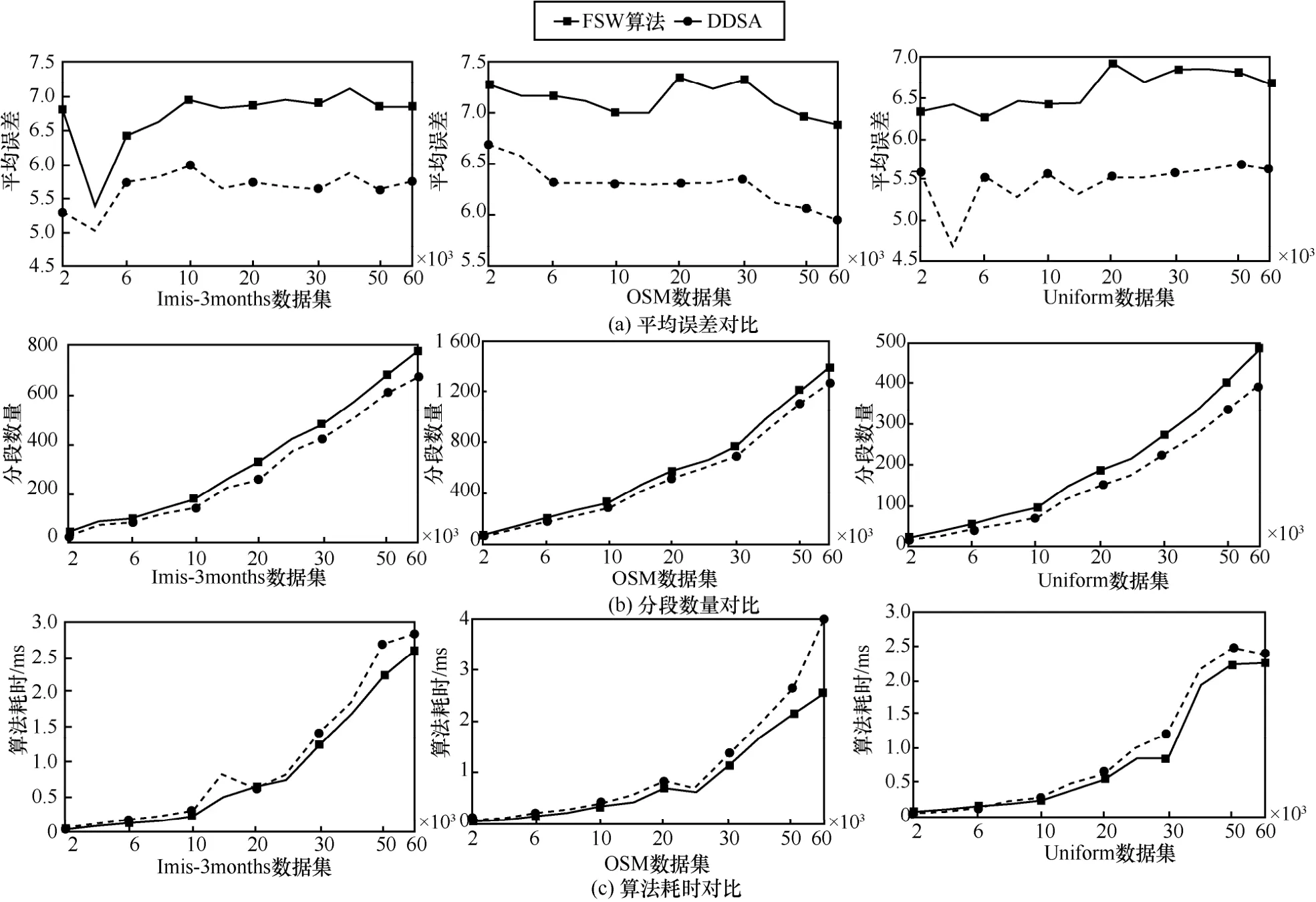
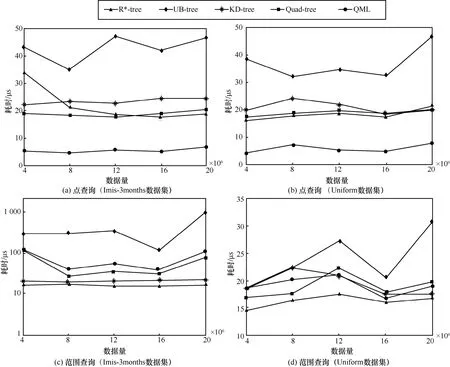
假设XY二维坐标系中有数据点p0,p1,…,pn近似二次多项式y=ax2+bx+c分布,对于每个数据点pi=(xi,yi) 如果满足xi 坐标系中二次函数采用式(1)的形式,其中a、b、c是该函数的系数 为了定位该曲线,将坐标系的第一个数据点p0(x0,y0) 和第二个数据点p1(x1,y1)放置在近似曲线上,可以得到 根据式(2)和式(3)可以得到参数a、b的映射关系 设置允许的误差范围为ε∈N+,即拟合曲线与数据点的距离在ε内。为了简化算法,本文将该距离近似为两者Y坐标轴的差值,假如第三个数据点p2(x2,y2) 满足最大误差的二次曲线分布,则有 利用式(5)和式(2),可以进一步得到 如图3(a)所示,式(4)描述为直线L0,式(6)和式(7)描述为平行线L11和L12之间的区域,因此可以得到参数a、b的可行区间[P11,P12]。当验证第四个数据点时,可以得到类似式(6)和式(7)的关系(图3(a)中平行线L21和L22之间的区域),该区间与直线L0相交于点P21和P22。因此区间[P11,P12]和[P21,P22] 重叠区域[P21,P12]即新的可行区间。重复该过程,直到可行区间为空。该算法通过不断缩小范围来得到分布相似的数据点并进行划分,其过程如图3(b)所示。 图3 SFCS 算法示意 SFCS 算法如算法3 所示。相比于算法复杂度为O(n) 的FCS 算法,SFCS 算法将多边形的可行空间计算简化为线性的可行区间计算,算法复杂度为O(1),虽然牺牲了一定的精确度,但是降低了算法的复杂度,提升了算法的运行速度。 对于QML 索引的范围查询可以视为对矩形区域的查询。给定查询矩形 qr=[xl,xu)[y l,yu),其中xl和yl分别表示x轴和y轴方向最小边界值,xu和yu分别表示x轴和y轴方向最大边界值。范围查询示意如图4 所示,先通过四叉树快速查找到与qr 有交集的单元格cell,然后将qr 查询分解为多个小矩形的并集 当查询的类型为lri(图4(b))时,索引会先计算其矩形区域的最小Z值和最大Z值。然后将Z值映射到模型曲线上(图4(c))获取可能的数据地址,对应的数据地址需要根据最大误差范围进行修正以保证覆盖率。因为模型曲线映射的数据范围大于查询的lri实际范围(图4(b)深色区域),因此需要对查询的数据进行校验再放入查询结果中。 图4 范围查询示意 给定一个数据点qknn=(x,y) 和一个距离值δ,以点qknn为圆心划定半径为δ的圆,将该圆内部区域定义为B(qknn,δ)。将B(qknn,δ) 包含的点按照与点qknn的距离由小到大排列,最终选取的topK个点即KNN 查询的结果。 QML索引采用空间密度估算KNN查询距离δ,将KNN 查询转化为递归和范围查询。QML 的KNN查询过程如图5 所示,通过构建矩形区域Q(qknn,δ),将目标区域B(qknn,δ)变为Q(qknn,δ)的内切圆,将查询B(qknn,δ)的点转化为查询Q(qknn,δ) 范围内的点。通过设置初始距离δ0,逐步扩展查询区域,直到查询结果满足K个或者距离大于最大查询距离δ。 初始距离δ0设置和扩展策略对KNN 查询算法至关重要。δ0过大或者或过小都会导致查询性能下降。为此本文提出QML 的空间密度测量方法。QML混合索引通过引入四叉树,尽可能地将数据进行等量划分,每个单元格 cell 包含的数据量不大于Cell_max_count。因此本文可以做出合理假设:空间cell 内数据点大致均匀分布,在此基础上计算cell=[l x,u x)[l y,uy)包含数据的空间密度 当要选取区域cell 内K个点时,可以根据空间密度估算距离δ0为 如图5 所示,此时可以先获取区域B(qknn,δ0)内的所有数据点。假设区域B(qknn,δ0) 内的数据点数量K′小于要查询的K,则需要对初始距离δ0进行扩展。在空间密度保持不变的假设条件下,B(qknn,δ1)的勒贝格测度是B(qknn,δ0) 的K/K′倍,因此可以推断出拓展后的距离为 图5 KNN 查询示意 给定查询点qknn=(x,y)、最大查询距离δ、返回结果数量K,QML 索引的KNN 查询过程如下。 步骤1初始化查询矩形qr 为空,查找点qknn所在的cell,并根据cell 的空间密度ρ和返回结果数量K计算半径距离δ0(式(11)); 步骤2比较δ0和最大查询距离δ,选择较小值为初始查询距离δ′; 步骤3使用qknn和δ′构建查询矩形然后计算qr′和qr ∩qr′的差集得到需要查询的矩形区域qr″; 步骤4查询矩形区域qr″得到可能的结果队列result′,遍历result′判断数据点是否在圆形区域B(qknn,δ′)范围内,如果在,则加入结果队列Lr中,否则加入等待队列Lw中; 步骤5对等待队列Lw中数据点做校验判断是否符合B(qknn,δ′) 的范围要求,符合则加入Lr中; 步骤6判断结果队列Lr中的数据量是否已经满足K个,满足则退出,不满足则使用式(12)重新计算δ′,并将现在的qr′赋值给qr,再次执行查询操作。 QML 的数据更新包括插入和删除操作,相应的更新算法同时支持单点更新和批量更新。 QML 的本地模型是基于有序数据排列完成的,当有新的数据加入时需要对数据进行重新排序和本地模型训练。这样的操作会消耗一定的计算资源。为了避免频繁的排序和模型训练,QML采用缓存插入的方式。当新的数据点要插入数据节点时,先加入等待插入的缓存队列,当缓存队列达到最大阈值时,再对节点进行重新排序和模型训练。 给定需要插入的数据点k=(x,y),QML 索引的插入过程如下。 步骤1通过QML 索引根节点查找到k所在的单元格cell,如果单元格cell 为空则初始化该单元格; 步骤2使用Z顺序曲线映射函数M计算k的Z值zvalue得到kz,使用单元格cell 的本地模型集合L对zvalue进行检索; 步骤3如果检索到zvalue所在位置数值为空,则直接将kz插入该点;如果检索到zvalue不存在,则先将该数据点加入cell 的缓存队列中,然后执行步骤4 的分裂检查机制; 步骤 4如果 cell 的数据量 size 大于Cell_max_count 或者缓冲区数据量大于缓冲区阈值则合并数据集,并对当前单元格cell 执行算法1 的数据划分操作。 考虑到更新效率,QML 索引在执行删除操作时不会直接删除索引,而是先将该索引处的数值置空,然后执行节点合并检查机制,当满足条件时再对单元格cell 重新构建。 给定需要删除的数据点k=(x,y),QML 索引的删除过程如下。 步骤1通过根节点查找k所在的cell,若cell不存在则直接返回false,否则执行步骤2; 步骤2通过Z顺序曲线映射函数M计算k的Z值得到kz,使用cell 的本地模型集合L检索kz的zvalue,若zvalue存在且数值不为空,则将该索引处的数值置空,然后执行步骤3 的合并检查机制; 步骤3获取cell 的父节点pCell,如果pCell的数据量小于Cell_max_count,则将pCell 赋值给cell,并递归使用步骤3 进行判断;当pCell 数据量大于Cell_max_count 时执行步骤4 并发送当前的cell; 步骤4将步骤3 的输出结果命名为newCell,若newCell 与初始cell 不同,即上层节点满足合并条件时,对newCell 执行算法1 的数据划分操作;如果newCell 和cell 是同一个,则比较cell 的数据量和其索引长度大小,若两者差值大于最大阈值,则对当前cell 执行算法1 的数据分段和模型生成操作。 本节从学习多维索引对比和实验验证2 个方面对构建的QML 索引进行评估。 QML 索引实现了ZM[8]、ML-Index[9]、LISA[10]、Flood[11]等学习多维空间索引所支持的各种功能,包括范围查询、KNN 查询、索引更新等,本文从数据布局、一维空间学习模型以及算法复杂度等角度对现有的学习多维空间索引进行了对比,如表2 所示。 表2 学习多维索引比较 QML 索引的数据布局采用四叉树和Z顺序曲线结合的方式,根据设计的DDSA 通过一次性数据遍历构建分段模型。QML 索引相比于其他学习多维索引的优势主要在功能实现和数据更新上。QML索引的范围查询时间复杂度为O(logn)+O(n),优于LISA 索引的O(n2)+O(n)。QML 使用树状索引作为中间节点保证了数据更新(插入和删除)的时间复杂度为O(1),相比其他索引具有更灵活的构建方式,能快速实现索引的动态更新。 因为实验数据的限制,本文的实验验证部分主要是将QML 索引和R*-tree[13]、KD-tree、Quad-tree、UB-tree 进行比较。本节实验包括实验设置、数据分段算法对比实验、参数影响、数据更新表现、范围查询表现和KNN 查询表现。 1) 实验设置 本文使用了如下的3 个空间数据集作为测试数据集。 ①Imis-3months 由专注于 AIS 技术和公共信息系统的公司 IMIS Hellas S.A.收集。删除重复项后,保留106 700 263 条记录。 ② OpenStreetMap(OSM)[28]由英国 Steve Coast 于 2004 年创建。本文从 OpenStreetMap 上获取了美国本土各类建筑、商店等标签的地理信息,去重后包含2 490 799 条记录。 ③Uniform 是通过对一定区域内均匀分布的数据进行随机采样产生的数据集,去重后的数据为20 000 000 条。 对比模型。为了验证本文提出的动态数据分段算法DDSA 和QML 混合空间索引的有效性,本文设计了如下的实验:将本文的DDSA 与传统的FSW算法进行比较,将QML 索引与4 种现有的索引R*-tree[13]、KD-tree、Quad-tree、UB-tree 进行对比实验。 评估指标。在数据分段算法实验中本文比较了FSW 算法和DDSA 在不同数据集下的表现。使用3个度量来评估数据切分算法的性能:平均误差Average Error、分段数量Number、算法耗时Time。 在空间索引对比实验中本文使用2 个度量来评估方法的性能:内存空间占用Size、索引操作耗时Time。对于每个数据集本文随机生成5 000 个查询矩形R和5 000 个KNN 查询点K,然后计算出每个索引类型进行查询操作的平均值并进行比较。 2) 数据分段算法对比实验 数据分段算法的效果与置信区间设置和数据集大小相关。为了综合评估FSW 算法和DDSA,本文在3 个空间数据集Imis-3months、OSM、Uniform 上分别选取记录数为{2 000,4 000,6 000,…,50 000,60 000}的测试集合M={m0,m1,…,m11},在每个测试集mi上设置置信区间{5,10,15,20,25,30}进行多次实验, 最后取平均值作为测试集mi的实验结果。在生成测试数据集时,本文按照四叉树划分算法进行等比例划分以更符合实际情况。通过比较2 种算法在不同数据集上的平均误差、分段数量和算法耗时来评估算法的性能。 实验结果如图6 所示。从图6(a)中可以看出,DDSA 比FSW 算法平均误差要小,经测算平均可以减少12%~17%的误差。这是因为DDSA 采用分段线性函数和二阶多项式函数对不同分布特征的数据分别进行拟合,更贴合数据实际分布规律。缩小平均误差可以减少QML 索引中间查询结果队列的数量,优化查询速度。 从图6(b)中可以看出,DDSA 相比于FSW 算法可以有效减少分段函数的个数,测试数据集越大,DDSA 效果越好。经测算DDSA 可以平均降低7%~10%分段数。减少分段数量可以有效降低索引的存储空间和维护成本,同时也可以更快地查找到目标数据的本地模型,从而加快索引速度。 从图6(c)中可以看出,DDSA 的时间消耗要比FSW 算法多,平均会增加13%~17%的耗时。这是因为DDSA 需要先进行线性函数的验证,如果不符合线性分布会再进行二阶多项式函数的验证,所以会不可避免地带来时间的损耗。 图6 FSW 和DDSA 平均误差、分段数量、算法耗时比较 在QML 检索应用中,对生成的数据分段先通过查找算法(以二分查找为例)找到对应的分段函数,然后通过该函数推测数据可能的位置,最后根据误差阈值进行校验(±ε)得到可能的结果队列。DDSA 相比于FSW 算法对QML 索引检索速度提高10%~13%。为了保证QML 索引性能,单元格最大阈值Cell_max_count 应设置在[10 000,30 000]范围内,过大或者过小都会降低索引性能。QML 索引的构建支持并发操作,当数据集比较大时,可以通过适当增加计算资源(1.13~1.17 倍)采用多线程的方式缓解DDSA 的算法耗时。 3) 参数影响 影响QML 索引性能的参数包括单元格最大阈值Cell_max_count 和本地模型的置信区间ε。为了研究这2 个参数对QML 索引空间大小、索引初始化时间和数据检索时间的影响,本文设计如下实验:从公开数据集Imis-3months 中随机选取40×106条记录作为测试集,将QML 的索引单元格最大阈值Cell_max_count 设置在[2 048,63 488] 范围内,将本地模型置信区间ε设置在[10,100]范围内,进行多次实验后取平均值作为实验的最终结果。 实验结果如图7 所示。从图7 中可以看出,QML单元格最大阈值Cell_max_count与QML索引空间大小成反比,与QML 索引初始化时间成正比,对QML检索时间影响不大。这是因为随着Cell_max_count的增大,QML 索引的叶节点数量随之减少,所以需要的存储空间变小。但是每个单元格cell 需要花费更多的时间构建本地模型,叶节点初始化和更新维护成本也会随之上升。当Cell_max_count 增加时,QML 索引的本地模型集合L也会变大,但是QML的中间节点减少,所以整体的检索速度变化不大。 图7 QML 参数影响三维立体 QML 检索时间和初始化时间随ε的增加逐渐波动上升。QML 索引空间大小随ε增加逐渐下降。当ε增加时,QML 索引本地模型的准确率会逐渐下降,这就使本地模型推算的结果队列增加,因此QML 需要花费更多的时间对结果队列进行校验,导致检索速度成本上升。同时随着ε的增加,QML 的单位模型可以容纳更多的数据量,使本地模型集合的分段数量减少,因此可以加快分段函数检索速度,减少模型集合空间大小。QML 索引准确率的影响要比分段数量带来的影响要大,这就使QML 检索时间和初始化时间随着ε的增加呈现逐渐波动上升,QML 索引空间大小随着ε的增加逐渐下降。 综合来看,QML 的索引参数Cell_max_count和ε设置应充分考虑QML 索引的具体应用场景。如果应用场景对索引空间占比要求较高,应适当调大2 个参数,如果对索引更新性能要求较高,应适当调小2 个参数。本文后续的实验中QML 索引最大单元格阈值设置为20 000,本地模型置信区间ε设置为10。 4) 数据更新表现 为了比较 QML 索引与传统的数据索引R*-tree、KD-tree、Quad-tree、UB-tree 在数据更新时的性能表现,本文设计如下实验:从数据集Imis-3months、Uniform 中按照区域选取记录数为4×106、8×106、12×106、16×106、20×106的数据构成测试数据集D={d0,d1,d2,d3,d4},对于每个数据集d选取其中50%构建初始数据集I,另外的50%作为额外的数据集E插入索引中。从I∪E中随机抽选50%的点作为要删除的数据集D。以上3 种配置上进行实验。Configuration Init 为初始化构建实验,使用I来构建所有的5 个索引。Configuration AI 为插入测试实验,使用E来进行插入操作。Configuration AD 为删除测试实验,使用I构建索引并插入E后,删除D中的数据。 实验结果如图8 所示。在Configuration Init 实验中,所有的索引结构耗时都随着数据量的增加呈线性增长。当数据量激增时,Quad-tree 的初始化性能会降低很多。除了Quad-tree,QML 索引耗时始终少于其他索引结构。在 Configuration AI 和Configuration AD 实验中,QML 索引呈现出近似O(1)的时间复杂度变化趋势,除Quad-tree 外的其他索引呈现O(n) 的线性变化。因为QML 使用了四叉树作为中间节点,所以QML 索引与Quad-tree 的数据更新操作效率相近。与最典型的树形索引R*-tree 对比,在Configuration Init 中,QML 索引平均耗时减少40%;在Configuration AI 中,QML索引平均耗时减少约80%;在Configuration AD 中,QML 索引平均耗时减少40%~60%。 图8 数据更新处理耗时比较 图9 显示了5 个索引结构在不同数据集下的内存消耗。从图9 中可以看出,QML 索引相比于传统的索引结构,存储相同的数据量时可以占用更少的内存空间。而且随着数据量的增加效果越明显。相比于R*-tree,平均可以减少约33%的存储空间。 图9 索引内存消耗比较 5) 范围查询表现 为了比较QML 索引与4 个传统索引范围查询的性能,本文设计如下实验:对于每个数据集本文随机生成5 000 个数据点,并构建查询矩形R,分别使用5 个索引进行点查询和范围查询,记录耗时。 实验结果如图10 所示。从图10 中可以看出,QML 索引在点查询方面呈现出相当大的优势。在范围查询中与其他索引基本持平。这是因为QML索引cell 的本地模型在推测目标数据位置时存在一定的误差(这也是需要设置置信区间的原因)。误差的存在导致QML 索引必须对模型检索的结果进行遍历校验。当检索的矩形区域范围扩大时,包含的数据点也会增多,QML 索引本地模型检索出的数据量也会增多,因此需要花费更多的时间进行数据校验。因为点查询过程只需要检索一个有效数据,所以QML 本地模型推算到的数据误差也就能保证在[−ε,ε]范围内。当QML 索引本地模型检索的数据结果长度小于传统树形索引结构需要遍历的深度时,QML 索引就能表现出优于传统树形索引的性能。 图10 点查询和范围查询比较 6) KNN 查询表现 对于每个数据集,本文随机生成5 000 个KNN查询点K,然后在索引QML、R*-tree 和KD-tree进行检索,记录返回的时间。最后对所有的检索结果取平均值。 实验结果如图11 所示。从图11 中可以看出,QML 索引的KNN 查询结果相比于R*-tree 和KD-tree 不是很稳定。原因在于QML 索引的KNN查询性能与数据分布特征有关。QML 索引的KNN查询算法引入了空间密度的概念,通过计算最小单元格cell 的均匀空间密度计算初始空间距离δ0。当单元格cell 内的数据有较大数据偏移时,会导致初始的空间距离δ0计算不精确,从而增加查询周期。同时cell 的大小也会对空间密度产生一定影响。如果Cell_max_count 偏大,必然会导致单元格空间密度的失真。如何增加QML 索引KNN 查询的稳定性是接下来的工作重点之一。 图11 KNN 查询比较 本文提出的QML 索引可以很容易拓展到n维空间领域。对于n维数据集可以使用2n叉树代替原有的四叉树结构,例如三维数据可以使用八叉树代替四叉树。使用n维子空间space 作为叶节点存储单位,space 存储单位阈值的数据。Z顺序曲线变换可以将n维数据降维到一维。DDSA 可以根据数据的分布规律增加多项式函数的类型以适应更复杂的曲线,比如三阶多项式函数。 在本文中提出了一种新的空间数据学习索引结构——QML。通过本文设计的动态数据分段算法DDSA,结合四叉树和Z顺序曲线构建的QML 索引可以利用空间数据分布规律优化检索速度。DDSA 保证了通过一次性的数据遍历构建索引模型。通过引入四叉树和Z顺序曲线,以cell 单元格为最小单位训练本地模型保证了单位索引相互之间的独立性。QML 索引在存储空间和查询速度上都达到了一个理想的效果,并能够灵活快速地实现索引构建和更新。QML 采用四叉树结构作为内部节点,因此可以进一步支持使用压缩方案与节点级压缩技术来减少索引的大小。它是学习索引在空间数据集上的一种新的尝试。



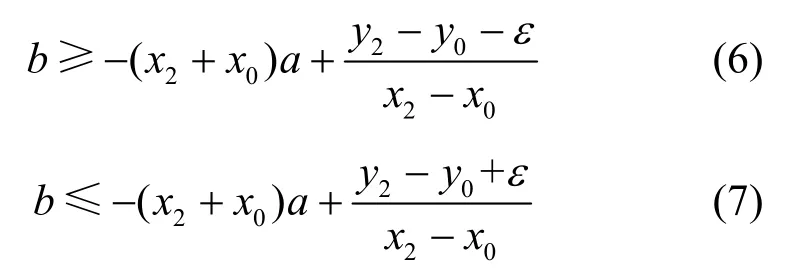


5 基于QML 的查询处理
5.1 范围查询
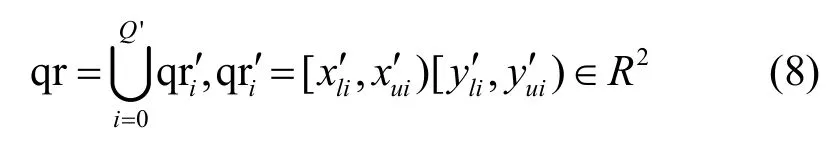


5.2 KNN 查询



6 QML 的数据更新
6.1 插入
6.2 删除
7 索引评估
7.1 学习多维索引对比

7.2 实验验证




7.3 高维空间的拓展
8 结束语

