基于旋转置乱的索引跳频抗干扰加密方法

鲁信金，雷菁，施育鑫

（1.国防科技大学电子科学学院，湖南 长沙 410000；2.国防科技大学第63 研究所，江苏 南京 210007）

1 引言

信息技术的飞速发展向未来通信的安全架构设计提出了全新挑战。无线信道的开放性使攻击者更容易窃取或者干扰信息传输，给无线通信系统带来了安全威胁。物理层安全技术[1]从物理层角度出发，利用无线信道的物理特性来改善无线传输的安全性。其中，基于无线信道特性的物理层密钥生成技术[2-4]可以使合法通信双方随时通过信道估计安全地获取时变的随机密钥，实现逼近“一次一密”的加密效果。此外，目前无线通信系统中已有很多相应的物理层安全技术用于物理层信息传输各个阶段，例如安全编码[5-6]、调制加密[7-8]、跳频扩频[9-10]等。

无线通信抗干扰是保证通信质量的重要手段。由于无线信道的开放性，恶意发送方可以很容易地探测到合法通信方所使用的频段、估计通信参数，进而实施干扰[11-13]。常规的抗干扰手段如跳频技术因具有抗干扰和保密性等优点而被广泛应用于高安全通信中[14]。跳频通信中，合法收发双方利用已知的跳频图案使信号的工作频点不断变化来躲避干扰信号的干扰。由于干扰方无法获取跳频图案预测工作频点的位置，当跳速足够快时，干扰方很难进行跟踪干扰，使跳频通信具备较强的抗干扰能力[15]。然而，无线系统中的电子攻击越来越严重，越来越多的研究者希望设计一种跳频方式可以保证在抗干扰的基础上实现安全无线通信[16]。

针对跳频通信抗反应式符号级干扰能力差的问题，文献[17]提出了索引调制跳频扩频（IM-FHSS,index modulation frequency hopping spread spectrum）抗干扰方法（本文中简称为索引跳频方法），利用多组跳频图案确定当前可用频点，用活跃频点的位置索引传输信息，在接收端提出了能量最大似然检测器，能够恢复索引信息，使反应式干扰机难以有效实施干扰，相比传统的频移键控跳频扩频（FSK-FHSS,frequency-shift keying frequency hopping spread spectrum），该方法的抗干扰能力更强。然而，IM-FHSS 在设计上仅考虑如何抗反应式干扰，未能在安全性上确保其传输的信息不被窃听者获取。具体地，当窃听者通过相同的设备获取了跳频图案时，其索引比特的安全性无法保证；当IM-FHSS 使用符号传输额外的信息比特时，其符号没有进行加密，极易被窃听者获取。而从抗干扰角度考虑，IM-FHSS 在活跃频点上传输的符号是固定的二进制相移键控符号（BPSK,binary phase shift keying）或者正交相移键控符号（QPSK,quadrature phase shift keying），使干扰者能够根据施加干扰后收发双方的收发指令判断干扰情况，不断调整干扰信号的功率和相位，达到最佳干扰。

针对该问题，本文提出一种基于旋转置乱的索引跳频抗干扰加密方法，简称加密的索引跳频（EIM-FHSS,encrypted index modulation frequency hopping spread spectrum）方法。本文的创新点主要如下。

1) 通过无线密钥对索引映射进行置乱，此时窃听者无法通过获取跳频图案与索引比特之间的映射关系获取信息。此外，星座旋转加密方法对索引跳频通信系统进行了符号旋转，窃听者无法获取活跃频点上承载的符号信息，使系统的安全性得到保证。

2) 对比已有的索引跳频方法，由于本文方法中星座的合法结构是由密钥决定的，此时干扰者采用反应式干扰（波形相关的跟踪干扰）难以对接收方信号的旋转角度实施预测，进一步增加了合法通信方的抗干扰能力。

3) 理论分析和仿真结果表明，本文方法不仅进一步加强了已有索引跳频方法的抗干扰性能，还在不影响系统可靠性的前提下进一步增加了系统的安全传输能力。

2 系统模型

本文的通信系统模型如图1 所示。其中，Alice表示信号发送方，Bob 表示合法接收方，Jack 表示干扰方，Eve 表示窃听方。首先，收发双方通过无线信道特征进行密钥生成获得共享密钥Key。密钥生成过程通常包括信道特征量化与信息协商2 个步骤，分别用于生成保密序列及纠正其中的不一致位。本文采用信道的相位响应获取密钥[18-19]。

图1 通信系统模型

随后，Alice 将进行调制及索引跳频加密后信息发送到无线信道中，Bob 的接收信号可以表示为

其中，E表示信号能量，x表示Alice 传输的单位能量的频域信号，h表示信道响应。假设信道幅度响应的变化可以忽略，在相干时间内，h可以表示为h=exp(jθh)。其中，θ h表示信道的相位响应，是一个在[0,2π]取值的常数；n表示信道中的高斯白噪声。

在合法信道中，Bob 接收到的是来自合法信道和干扰信道上的信号，通过索引跳频解密及星座解旋转恢复有效信息。Jack 利用接收到的信息分析其调制类别和其参数信息，用相同的调制类别和参数调制随机比特流来干扰Bob，以实现高干扰效能的反应式符号级干扰。Eve 通过无线信道进行信息窃听和破译，希望获取合法通信双方所传输的信息比特。

假设接收方可以补偿信道相位响应，则合法接收方收到的信号可以表示为

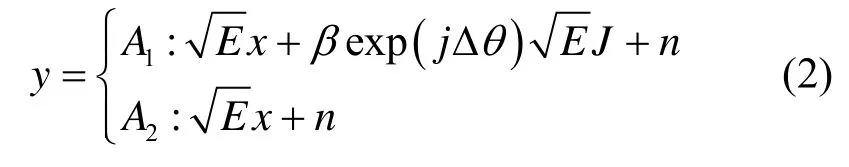
其中，J表示干扰方Jack 施加的干扰，且具有与x具有相同的调制方式和能量；β表示干扰信号与信号的功率差异比，β＞0 ；Δθ表示干扰信号与原信号的相位偏差；A1表示信号被成功干扰的情况；A2表示信号没有受到干扰的情况。设成功被干扰的时间在整个信号发送时间的占比为干扰率由于通信系统对传输的信息比特往往采用了深交织操作，使连续的干扰信号等价于以一定概率施加到各个符号上，因此干扰率可以表示为受到干扰的符号与所有传输符号的比值。

2.1 发射端的系统模型

发射端的系统模型如图2 所示。当每个跳频周期预发送m比特信息时，比特分割器将m比特划分为2 个部分，即m1比特和2m比特，并进行串并转换以便后续处理。其中，m1比特是由当前多路跳频图案确定的可用频点中激活频点的索引位置传输的索引信息，m2比特是由活跃频点上的BPSK 或QPSK 符号承载的符号信息。

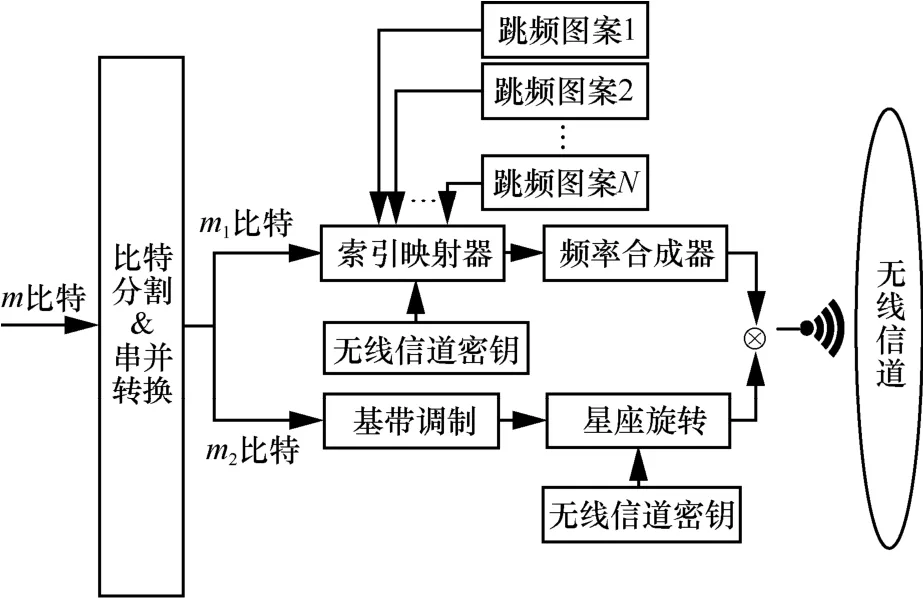
图2 发射端的系统模型

当发送的m1比特到来时，系统根据索引映射器选择其中的一路跳频图案作为活跃频点，并利用频率合成器合成该频点的载频信号。对于未加密的索引映射器而言，表1 中的比特与跳频图案的序号是相同的，这使窃听者能够根据已知明文对使用的跳频图案进行推测。为了使索引映射器的映射关系具有安全性，本文利用无线信道密钥对索引映射器的映射关系进行随机置乱，未加密和置乱加密的索引映射器分别如表1 和表2 所示。

表1 未加密的索引映射器

表2 置乱加密的索引映射器

对于2m比特，由于一般的索引跳频方法根据调制方式直接进行BPSK 或QPSK 调制，使窃听者能够对活跃频点进行侦察和分析，从而进一步获取m2比特的信息。为了解决这一问题，本文在基带调制的符号上采用二维的星座旋转加密后再上变频至选中的活跃频点，使窃听者由于没有无线信道密钥信息，无法解调出正确的符号进行判决。

最后，发送端再将星座旋转后的符号与所选载频的相乘，符号被上变频并发送到无线信道中。

2.2 接收端的系统模型

接收端的系统模型如图3 所示。由于在每个符号传输时刻，收发双方均具有相同的N路跳频图案，因此接收方可以通过频率合成器合成N路载频，并且将接收到的信号分为N路进行下变频以寻找活跃频点的位置。然后，接收方通过低通滤波器对N路数据滤除高频分量，得到低频信号。显然，只有活跃频点上的信号才具有较高的能量，其余信道仅有高斯白噪声。因此，经过能量检测器后，可以获得最大能量所在的跳频图案的位置，并输入索引解映射器。最后，通过无线信道密钥发生的置乱恢复后，接收端将恢复正确的索引比特信息。对于活跃频点上的符号，也通过无线信道密钥对星座解旋转后，即可解调恢复2m比特。

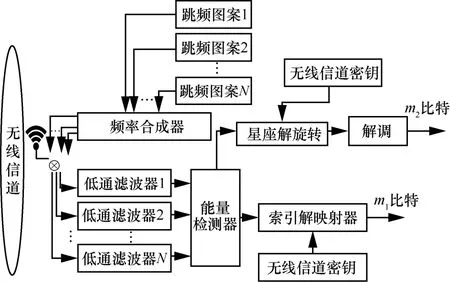
图3 接收端的系统模型

3 方法设计

3.1 索引映射器的置乱加密

未加密的索引映射表可以用一个单位矩阵IN表示，如图4 所示。矩阵中的1 所在的列表示数据信息，矩阵中的1所在的行表示该数据信息对应的跳频图案的序号。显然这样的映射关系无法保证安全性。

图4 未加密的索引映射表

本文通过无线密钥对映射表进行置乱，置乱加密后的映射表R可以表示为

其中，为置乱矩阵，由算法1 生成。

算法1置乱矩阵→的生成算法

输入通过无线信道提取的无线信道密钥[2]

输出置乱矩阵

1) 根据使用的跳频图案的数量确定索引映射器的大小N，并从无线信道密钥M中选取N个密钥k i,i=1,2,…,N；

2) 计算yi=106ki-floor(106k i),i=1,2,…,N,即取密钥小数点后6 位以确保初始密钥之间的不相关性；

3) 对yi由大到小排序，并将排序序号存储于向量ly中，其中ly是一个1×N的行向量；

4) 建立一个N×N的矩阵P，其第一列元素都为1，其余元素均为0，作为置乱矩阵的初始矩阵；

5) 根据ly第i个位置的值l y(i)，对矩阵P的第i行的元素1 右移l y(i) -1，遍历i=1,…,N；

由算法1 可知，原映射表与置乱矩阵相乘后，置乱加密后的映射矩阵R在任意行有且只有一个元素1，使索引映射表仍然能够保证一一映射。由于原映射表可以简单表示为单位矩阵，因此最终的映射表可以直接由置乱矩阵表示。注意到由于置乱矩阵的元素1 不再简单地沿对角线分布，窃听者需要遍历所有的映射可能才能恢复出正确的数据。对于合法接收方，由于拥有相同的初始密钥，其能够获得相同的置乱矩阵→通过对置乱矩阵→取逆，即可获得解索引映射器的对应关系。

3.2 符号的二维星座旋转

对于活跃频点上传输的符号，其星座图未经过加密处理，其相位、功率信息在长时间的传输中是不变的，容易被Eve 与Jack 所获取。对于Eve 来说，可以对活跃频点上的符号直接解调就可以窃听到信息。对于Jack 来说，可以在活跃频点上发送功率、调制方式均相同的反应式干扰信号，以实现最佳干扰。

因此，在本文中利用二维星座旋转来实现安全传输和抗干扰的双重目的。对于m2比特，由于一般的索引跳频方法是根据调制方式直接进行BPSK 或QPSK 调制，活跃频点上发送的信号经过二维星座旋转后可以表示为

其中，fc表示载波频率；φM表示基带为MPSK 调制时的相位值；φθ表示由密钥控制的随机旋转角度当M=2时，，当M=4时时BPSK 旋转前后的星座图如图5 所示。图5(a)和图5(b)为加噪前BPSK 星座图及其加密旋转后星座图，可认为其为发送方的星座图；图5(c)和图5(d)为加噪后BPSK星座图及其旋转后星座图，可认为其为经过高斯白噪声信道后接收者的星座图。

图5 M=2 时，BPSK 星座旋转前后星座图比较

M=4时QPSK旋转前后的星座图如图6所示。从图6 可以看出，星座图在星座旋转加密后呈环状，相位信息被完全打乱，没有明显的调制模式，原始信息得到隐藏。由于合法接收方具有共享密钥Key，其可以通过φθ值对每个接收到的符号进行解旋转。由于无线信道的空时唯一性，窃听者无法通过无线信道提取出和收发双方一致的无线共享密钥，因此无法恢复旋转的符号。

图6 M=4 时，QPSK 星座旋转前后星座图

本文进一步使用星座量化信息熵来测量星座混淆程度，其定义为

BPSK 和QPSK 旋转前后的信息熵如图7 所示。从图7 可以看出，无论是加噪前还是加噪后，对于调制方式BPSK 或者QPSK，旋转加密后的星座图较未旋转加密的星座图其信息熵有显著的提升。因此，本文方法可以显著提高星座熵，使星座高度混乱并且星座信息的泄露较少，安全性可以得到保障。此外，在抗干扰角度上，由于IM-FHSS 在活跃频点上传输的符号从之前的固定调制方式（BPSK 或QPSK）变成圆环，干扰者无法通过合法双方的相位调整获得最佳干扰方式。

图7 BPSK 和QPSK 星座旋转前后的信息熵

4 复杂度分析

相比于传统的索引跳频方法，加密的索引跳频方法增加了2 个加密过程，即索引映射器的置乱加密和符号的二维星座旋转，这带来了额外的复杂度。本节针对这2 个过程的复杂度进行了分析。

在映射表的置乱部分，包含一次对N个密钥计算提取小数点后的位数作为初始密钥，其中N=2m。随后对N个数进行排序，假设采用冒泡排序，其最大复杂度为次比较。对于置乱矩阵的生成，算法1 的步骤5)中，矩阵内元素1 的移动可以利用排序结果的序号对矩阵直接赋值，因此复杂度可以忽略。

在星座旋转部分，首先利用密钥映射出当前的旋转角度φθ。具体可以由已归一化的密钥（0～1均匀分布的随机数）乘以2π，需要一次乘法。随后，由当前的 BPSK/QPSK 符号乘以复数符号exp(j)θφ，因此需要一次复数乘法，即4 次乘法与3 次加法。

5 仿真分析

图8和图9比较了加密的索引跳频方法与一般的索引跳频方法在符号级反应式干扰下索引比特的误比特率。由于2 种方法的活跃频点上的符号比特受到干扰时误比特率均将显著提高，这里主要仿真索引比特的误比特率。本文注意到，一般的索引跳频方法的合法发送方发送的BPSK 或者QPSK 信号可以被窃听者分析，因此假设对合法方最差的情况，即干扰方在活跃频点上发送的BPSK 或者QPSK 星座图与合法发送方的星座图在合法接收端处不存在相位偏差，即Δθ=0 。此外，由于加密的索引跳频发送经过星座旋转的BPSK 或者QPSK 符号的相位在0～2π 是随机的，因此反应式干扰机也发送同样形式的信号进行干扰。比较2 种方法的误比特率结果可见，在干扰功率相近时，加密的索引跳频方法具有更低的误比特率，这表明其抗反应式干扰的能力更强。这是由于在加密索引跳频方法中使用了随机旋转的星座图，使干扰方将活跃频点上的符号抵消的概率降低。

图8 发送信号为BPSK 时，加密的索引跳频方法与一般的索引跳频方法在符号级反应式干扰下索引比特的误比特率

图9 发送信号为QPSK 时，加密的索引跳频方法与一般的索引跳频方法在符号级反应式干扰下索引比特的误比特率

图10 和图11 比较了发送信号分别为BPSK 和QPSK 时，加密索引跳频与索引跳频、已知跳频图案的窃听者在无干扰条件下的平均误比特率。此时跳频图案数设置为N=2、N=4、N=8。由于窃听者可能通过截获设备的方式获取相同的硬件设备，因此假设窃听者已经获取了跳频图案。由于窃听者没有与发送方相同的无线信道密钥，其索引映射器与星座解旋转时无法正确恢复索引比特信息与符号比特信息。因此误比特率始终为0.5，证明所提方法提高了系统安全性。此外，与传统的索引跳频方法相比，加密的索引跳频方法误比特率没有明显的区别。这是由于加密的索引跳频方法不改变信号的欧氏距离，当正常解密后，其信号形式等价于传统的索引跳频方法。因此，所提方法在提升传统索引跳频方法安全性的同时，对系统的可靠性不会造成影响。

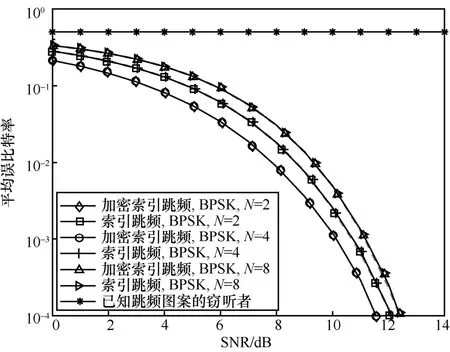
图10 发送信号为BPSK 时，加密索引跳频与索引跳频、已知跳频图案的窃听者在无干扰条件下的平均误比特率比较

图11 发送信号为QPSK 时，加密索引跳频与索引跳频、已知跳频图案的窃听者在无干扰条件下的平均误比特率比较

6 结束语

本文中，收发双方首先利用无线信道密钥生成技术产生共享加解密密钥。随后利用密钥产生置乱矩阵，对跳频图案与索引比特之间映射关系进行加密控制，使窃听者无法获取活跃频点上承载的符号信息，保证了系统的安全性。此外，发送端采用星座旋转加密方法对索引跳频通信系统进行了符号旋转，进一步增加了合法通信方的抗反应式干扰能力。接收端利用密钥对跳频图案及索引比特的映射矩阵进行解密，并进一步对符号信息进行解旋转。仿真分析结果表明本文设计的加密的索引跳频方法加强了原方法的抗干扰能力，并提高了系统的安全性。在后续的工作中，考虑设计更高效的索引映射器的置乱加密方法，以降低索引映射置乱加密过程的复杂度，提升系统性能。