运用概率论学习研究培养数学思维
■陈丽萍
(山西省贸易学校,山西 太原 030012)
数学思维从分析能力角度划分包括逻辑思维、形象思维、空间抽象思维等;按数学知识内容划分包括代数思维、几何思维、微积分思维、概率统计思维等,是指在实际应用过程中,运用相关的数学思想和方法思考和解决问题的能力,抓住问题本质规律,发现内在联系。可以说,数学思维在把数学知识应用到其他领域发挥着无与伦比的重要作用。所以我们常用对称美、和谐美、平衡美等来形容数学是优美的,其实质是思维之美,散发思想光芒。
概率论是基于随机现象的一种数学模型,是具体研究随机现象数量规律的一个数学分支,是用特殊的数学语言描述、分析、研究,透过现象看本质,搭建随机现象与数学其他分支联系的桥梁。在自然界和人类社会中,存在大量的随机现象,而概率是衡量该现象发生的可能性的量度,为其他学科提供了解决问题的新思路和新方法,概率论是社会科学发展的必然成果,分析过去预测未来,实质就是概率问题。“概率论是生活真正的引路人,如果没有对概率的某种估计,我们将寸步难行无所作为。”学习概率论研究其起源,可以帮助学生提炼醒悟思想,培养发展数学思维。
一、概率论的学习研究
(一)概率论的起源
概率论的起源与赌资有缘,引例:设想小张和小李打赌(可以是任何赌法),各出50元,先赢6局者拿走100元。但是小张赌到5:3领先时被迫停止不能继续。现在的问题是:100元中小李应该分到多少钱?
分法 1(平分法,1:1,小李分到 50 元)
分法 2(通吃法,1:0,小李分到 0元)
分法 3(朴素法,5:3,小李分到 37.5 元)
分法 4(概率法,7:1,小李分到 12.5 元)
分法 5(极大似然法,485:27,小李分到 5.27元)
按取得最终胜利的可能性来分。小张只需再胜1局就赢,而小李需要连胜3局才能赢。假设胜1局的可能性都是1/2,则小张赢的可能性应该小于1/2,小李赢的可能性是。
按最终赢的可能性来分析,胜1局的可能性不应该是1/2,而应该根据当前比分作最大似然估计,即小张胜1局的可能性为5/8,小李胜1局的可能性为3/8。最后小李赢的可能性是(。
又如古代很多数学爱好者喜欢用掷硬币试验,来计算硬币正反面抛掷频率,为研究随机现象和概率论发展提供了大量的详实的数据(见表1)。
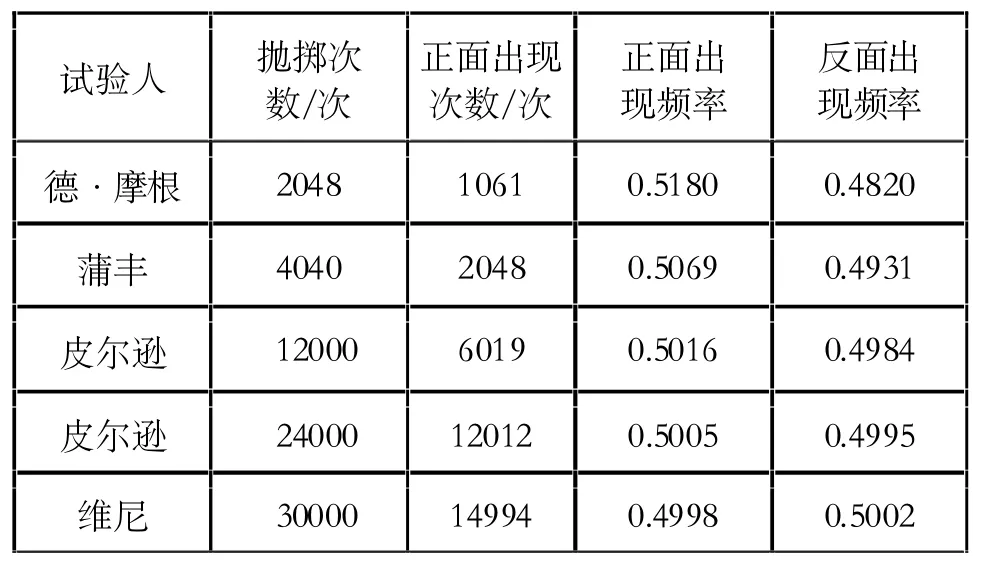
表1 掷硬币试验统计表
(二)概率论的研究对象
概率论研究内容包括:概率论基本概念、一元和多元随机变量及其分布、随机变量的数字特征、大数定律和中心极限定理、统计量及抽样分布、参数的点估计与区间估计、参数的假设检验及概率分布的拟合检验、方差分析与回归分析。
数学教学中掌握概率的定义和计算,用随机变量概率分布及数字特征研究“随机现象”的规律是教学重点。了解数理统计的基本理论与思想,能够熟练应用掌握包括点估计、区间估计和假设检验等基本统计推断方法是教学难点。解决重点突破难点从随机现象和变量开始,理解几何分布,从生活实际中引例,提高解决问题的兴趣,应用拓展能力。
1.随机现象
相对于确定性(决定性)现象而言,随机现象如某个城市每天发生的交通事故次数?某种新药在临床试验中是否有效?买彩票是否中奖?下一分钟股票价格是否会涨?
2.随机变量
随机取值的变量就是随机变量,随机试验的结果其实就是随机变量,随机变量的函数仍是随机变量。随机变量有两种,一种是离散型随机变量,一种是连续型随机变量。我们常用希腊字母ξ、η等表示随机变量。
(1)离散型随机变量:是指对于随机变量取值可能是有限个,也可能是无限个,但可以顺序列出,这样的随机变量就称之为离散型随机变量。
(2)连续型随机变量:是指对于随机变量的取值,是在某一区间内的一切值,无法按一定顺序列出,这样的变量就称之为连续型随机变量。
(3)两种随机变量的区别与联系:二者都是用变量表示随机试验的结果;但是离散型随机变量的结果可以按一定顺序列出,而连续性随机变量的结果不可以按一定顺序列出。
若 ξ是随机变量,η=aξ+b,a,b 是常数,则 η 也是随机变量,并且不改变其属性(离散型、连续型)。
3.研究随机现象
我们需要做大量的随机试验,通过不同的结果理解分析“随机事件发生”概率。
a.试验在相同条件下重复进行;
b.试验结果多样性,但可以预知所有结果的取值范围;
c.试验前无法预测会出现什么结果。
例如:某省级射击运动队对奥运选拔射击A选手和B选手的射击情况进行跟踪记载,见表2和表3。

表2 A选手射击所得的环数ξ的分布列

表3 B选手射击所得的环数ξ的分布列
求此奥运选拔A、B射手“射击一次命中环数≥7”“射击一次命中环数≥8”的概率分别是多少?提出选拔建议。
分析:该事件实际是典型的互斥事件,根据互斥事件的概率加法公式,“射击一次命中环数≥7”是互斥事件“ξ=7”“ξ=8”“ξ=9”“ξ=10”的和,同理“射击一次命中环数≥8”是互斥事件“ξ=8”“ξ=9”“ξ=10”的和,解法如下。
解:根据跟踪记录环数ξ的分布列,“射击一次命中环数≥7”的概率计算如下。
A 选手:由于 P(ξ=7)=0.09,P(ξ=8)=0.28,P(ξ=9)=0.29,P(ξ=10)=0.22。所求的概率为P(ξ≥7)=0.09+0.28+0.29+0.22=0.88。
B 选手:P(ξ=7)=0.08,P(ξ=8)=0.28,P(ξ=9)=0.39,P(ξ=10)=0.14。所求的概率为 P(ξ≥7)=0.08+0.28+0.39+0.14=0.89。
根据跟踪记录环数ξ的分布列,“射击一次命中环数≥8”的概率计算如下。
A 选手:由于 P(ξ=8)=0.28,P(ξ=9)=0.29,P(ξ=10)=0.22。所求的概率为 P(ξ≥8)=0.28+0.29+0.22=0.79。
B 选手:由于 P(ξ=8)=0.28,P(ξ=9)=0.39,P(ξ=10)=0.14。所求的概率为 P(ξ≥8)=0.28+0.39+0.14=0.81。
从本次跟踪分析,B选手“射击一次命中环数≥7”和“射击一次命中环数≥8”的概率均大于A选手的相应概率,由此结果可为奥运选手选拔提供依据。
4.研究事件关系及运算
(1)根据随机变量的概率分布列,求随机事件发生的概率。
(2)伯努利分布:研究对象是两点分布,两点分布列的应用非常广泛。它是一种常见的离散型随机变量的分布,是概率论中最重要的分布之一,比如彩券中奖几率、投篮命中几率、工厂产品检验合格率、股票基金波动等等现象,都可以用两点分布列来研究其规律。
如果随机变量X的分布列为两点分布列,就称X服从两点分布,而称P=P(X=1)为成功概率,两点分布又称0—1分布,由于只有两个可能结果的随机试验叫伯努利试验,所以这种分布又称为伯努利分布。
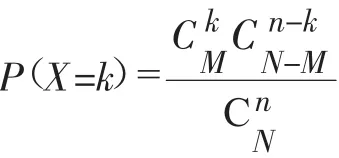
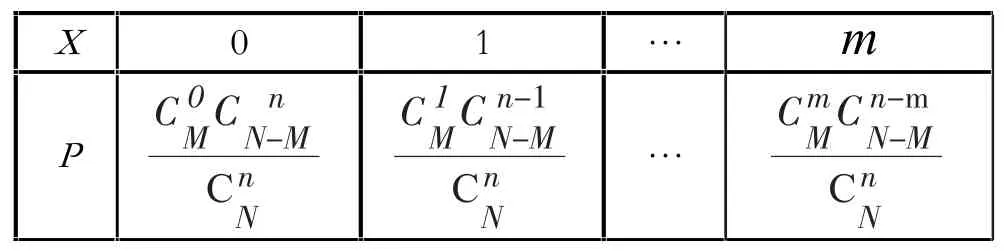
X 0 1 … m P …C0 MCn N-M C1 MCn-1 N-M Cm MCn-m N-M Cn N Cn N Cn N
5.几何概率揭示生活真理
(1)零概率事件不一定不发生。
(2)不是所有的事件都可以计算出概率。
也就是说,对任意的随机事件A,P(A)不一定都有意义。因此,有关样本空间的选择至关重要,哪些子集可算作随机事件的问题,需引入概率公理化定义。
如利用公式计算概率:某城市有N辆卡车,车牌号从1到N,有一个外地人到该城去,把遇到的n辆车子的牌号抄了一遍,当然有可能重复,求抄到最大号码正好是k的概率。
分析:记Bk是“抄到的最大号码不超过k”,Ak是“抄到的最大号码等于k”则有:Ak=Bk-Bk-1。
又如利用一般加法公式可计算有奖销售概率:一袋包装完好的食品中放一张奖券,n张不同的奖券为一套,收集齐一套可获大奖,求购买k袋食品收集齐一套奖券的概率。
二、概率论与其他数学知识的融合
概率论应用几乎遍及所有科学技术领域,概率估计不仅是数学学习重点,也是现实生活中的常见问题。融合有利于数学思维的形成,教师在教学中需要探索概率与其他知识点的交汇融合,培养学生动手探究习惯,层层递进,举一反三,发散思维,加强实验训练,尤其是要认真审题、梳理脉络、理清知识点,把握本质内涵,完善知识体系结构,才能解决各类知识点融合复杂的难题,进而提升学生的数学综合应用能力。
(一)概率与不等式知识融合
有效盘活学生学习思维,为概率学习与不等式学习带来全新思路,从概率的角度去分析不等式问题,进一步加强对复杂不等式的理解,不等式是数学学习的起点,发散思维的形成有助于后续复杂数学问题的迎刃而解。
(二)概率与代数方程知识的融合
如关于游戏闯关的一道题目,第一关掷骰子1次,第二关掷骰子2次,以此类推第n关掷骰子n次,规定只有第n关的n次骰子点数之和超过n的二次方才算游戏闯关成功,请问这一关游戏最多能够连过几关?连过两关的概率是多少?列出方程求解,这就是概率与方程的典型融合。
(三)概率与排列组合知识的融合
如针对电子专业的学生,结合物理电路方面的知识思考:由五个接收器与一个信号源构成一个串联线路来接收信号,如果将左、右侧的六个接线点分别随机地各分为三组,然后将所有六组的两个接线点用导线连接,请问这五个接收器可以同时接受信号的概率是多少?
三、培养数学思维是高质量教育发展的必须
(一)高质量教师的正确引导
高质量的教育需要高质量的教师,数学是思维的体操,提高学生的数学思维能力,这就需要教师的正确引导,作为公共基础性数学课程,对学生数学思维的培养得天独厚、责无旁贷。做中教、做中学,学中做,循循善诱,诱导启发学生“口、手、脑”全用,“讲、演、练”齐动,课堂精讲、网络辅学、实践延伸,引导学生主动思考感悟,调动主观能动性、发挥主体作用,在相互讨论和启发中开展高质量思维活动,在活动中学习、发展、创新,教师要做活动的引导者、组织者、参与者,为学生成长导航。
(二)数学思维魅力展望
学习数学的过程其实苦中做乐,要有足够的勇气与毅力,要有逢山开路、遇水搭桥的魄力,要忍受漫长而孤独的研究过程,独自品尝成功的喜悦和失败的沮丧,这就是数学思维的无限魅力。我们最早可追溯到18世纪古代著名的哥尼斯堡七桥问题:当时欧洲东普鲁士哥尼斯堡的城市近郊,有一条河叫普雷盖尔河,大河穿城而过,河中间有两个岛,在两个岸和两个岛之间共架有美丽的七座桥,成为当地居民休闲娱乐的好去处。当时城中居民热烈地讨论:如果步行从一个地方出发,想一次性而且不重复地走遍七座桥,最终还能回到原始出发点,这种想法可能实现吗?这个问题引发无数学者热议。数学家欧拉把七桥问题转化成特殊路径的思考方法,严格证明了这样的特殊路径根本不存在,为热议的七桥问题画上了圆满句号。欧拉这种极具代表性的思维范式直至今日对我们思考问题和分析问题仍有很强的指导意义和现实意义。
适应新时代、新挑战、新机遇,在教育教学过程中师生只有真正体验到应用数学思维解决实际问题的畅快淋漓、妙不可言,才能真正感悟"数学为自然科学之源"的论述是多么的精辟,才能对具有数学思维魅力的拥有无限向往。

