糙米的碾白过程模拟及破碎影响分析

张 强， 廖 敏*， 杨亚军， 张晓鸥

(1.西华大学机械工程学院， 成都 610039； 2.西华大学现代农业装备研究院， 成都 610039)

稻谷是中国主要粮食作物之一，随着人们生活水平的逐渐提高，对大米的品质要求也逐步上升，目前评价稻米加工品质最常用的是整精米率[1]，并且整精米的价格是碎米的2～3倍[2]。限于目前的碾米技术碎米率仍处于10%～25%[3]。小型碾米机多采用单次加工的碾米方式，碎米率高于大型碾米厂多机轻抛[4]的方式。由于近年来出现了食用鲜米的热潮，市场上出现了大批小型智能鲜米机。因此，探索小型碾米机降低碎米率的方法极其重要。

糙米是实实在在的颗粒物料，在加工过程中运动轨迹不规则、受力不均、记录运动过程复杂等特点[5]，而颗粒流离散元法将研究实体具化为一个个实实在在的球体，基于分子动力学理论及经典力学理论研究每一个球体的受力、运动及能量转化[6]，通过离散元技术能够观察到碾米过程中米粒的实时堆积状态，获得米粒的速度和力学信息[7]，使得人们能够从微观颗粒入手研究糙米加工过程的宏观性质。现将糙米在碾白室内的运动化分为轴向运动、径向运动以及翻滚运动[5]，利用EDEM模拟糙米在碾白室内运动情况，分析糙米的运动以及碾白室结构对碎米率的影响。

1 糙米的离散元模型

基于离散元技术，采用EDEM软件对糙米碾白过程进行模拟，建立了两种糙米离散元模型：Hertz-Mindlin黏结接触模型和糙米球元模型[8]。Hertz-Mindlin黏结接触模型是使用EDEM软件生成给定数量的颗粒后再由挤压模型确定颗粒位置形成米粒球团，由API(automated pellet inspection)颗粒插件完成颗粒的转换，最后由API黏结模型插件使米粒球团内部颗粒相互粘接形成糙米模型；糙米球元模型是将4个直径不同的球体组合填充得到的糙米模型。

在设计糙米碾白的模拟过程中，为了便于观察糙米在碾白室的实时碎裂情况,因此采用粘接键可断裂的Hertz-Mindlin黏结模型模拟糙米碾白过程，如图1所示。

图1 糙米黏结模型Fig.1 Brown rice bonding model

在仿真过程中，共使用4 000粒糙米模型模拟碾白过程，若全部使用糙米黏结模型，会造成整个模拟过程非常缓慢，最终将模拟实验用到的糙米模型进行调整，将原试验中4 000粒糙米粘结模型替换3 000粒球元模型，如图2所示。

图2 糙米球元模型Fig.2 Spherical element model of brown rice

2 糙米破碎因素分析

糙米破碎的影响因素主要有稻谷品质、碾米工艺、碾辊的材料、碾米压力[9]、碾白室结构。碾米工段占总增碎的60%以上[10]，碾白室作为碾米机的核心部件，主要考虑碾白室对糙米的运动、受力以及碎米率的影响因素为米筛边数的改变与碾辊结构的改变。

2.1 米筛边数

碾白室主轴在实验过程中长度保持不变，为了确保实验的实效性，改变米筛边数时筛长和体积保持不变，在此条件下需要保证不同边数的米筛的截面面积一致，则米筛的外接圆半径R需要满足[5]关系式

(1)

式(1)中：A为截面面积；ξ为边数。本实验采用边数为四、五、八的正多边形米筛与正六边形米筛对比，根据式(1)，计算各多边形外接圆半径，再将多边形米筛简化取整，根据多边形与外接圆的关系得出不同边数米筛的边长、轴筛最窄距离、轴筛最宽距离，简化后的六边形米筛截面尺寸如图3所示。本文中所涉及的不同边数的米筛简化后具体参数如表1所示。

图3 简化六边形米筛的截面尺寸Fig.3 Simplified cross-section size of Hexagonal rice screen

表1 简化后米筛截面参数Table 1 Simplified cross section parameters of rice screen

如表1所示，碾辊轴旋转所形成的圆截面与米筛的轴筛最窄距离随着边数的增加而逐渐增大，由5.33 mm增大至7.67 mm，而轴筛最宽距离随着边数增加逐渐减小，由15 mm减小至10 mm，由此可见，不改变多边形米筛的截面面积与体积的情况下，边数改变后会导致截面空间布局发生规律性的改变。

2.2 碾辊结构

碾辊结构主要包括碾筋高度、碾辊直径、碾筋个数，根据六边形米筛，对碾辊结构模型参数多次调整进行模拟实验并与未改变参数的碾辊模拟实验的结果对比[5]，最终碾辊结构调整方案为：增加碾筋高度、减小碾辊直径和增加碾筋个数，如表2所示。

表2 碾辊模型参数Table 2 Roller model parameters

3 基于离散元的糙米碾白过程模拟

3.1 米筛边数改变对糙米运动及破碎的影响

3.1.1 糙米径向运动分析

在模拟过程中，糙米沿X轴、Z轴的运动速度即为碾白室内的径向运动速度，米粒在碾白室内径向运动速度越大，糙米获得的易位能力就越大，保证糙米能够充分碾磨。本文中研究的对象是小型卧式碾米机，在探究碾白室结构改变对糙米径向运动的影响时需要考虑糙米自身重力因素的影响，为避免重力因素造成实验数据不精确，所以分开讨论改变碾白室结构对糙米径向运动的影响。

图4为模拟六边形米筛碾米过程中糙米沿Z轴运动速度变化趋势，绝大部分米粒的速度趋于负半轴，处理图4中的数据得出糙米的平均运动速度为-22.01 mm/s。而实际情况中，米粒堆积于碾白室下方、且数量大，这说明无法通过碾辊转动带动米粒来抵消重力对糙米运动造成的影响[11]，造成碾白室内的大部分糙米趋于Z轴负方向运动，糙米堆积于Z轴负方向一侧(碾白室下方)，导致糙米与米筛反复磨削。

图4 六边形米筛糙米沿Z轴运动速度变化趋势Fig.4 Change trend of movement speed of hexagonal rice sieve brown rice along Z-axis

图5是几种不同边数米筛中糙米沿Z轴方向的平均速度，速度方向与重力方向一致。对比正五边形、六边形、八边形米筛，轴筛最宽间隙逐渐减小，而糙米沿重力方向的运动速度直线增加，糙米自身重力因素对运动的影响逐渐增强。对于小型卧式碾米机来说，糙米在碾白室内沿重力方向的易位能力随米筛边数的增加而减弱，其中糙米自身重力因素对Z轴方向运动速度影响最大的是四边形米筛，说明过小的轴筛间隙会影响糙米在碾白室内易位能力，而在四边形米筛中糙米沿重力方向的速度最大，使得糙米堆积于碾白室下方。

图5 糙米在不同边数米筛中沿Z轴方向运动速度Fig.5 Speed of brown rice moving along Z-axis in rice sieve of different number of meters

如图6所示，在正六边形米筛中糙米沿X轴方向的平均运动速度比较集中，去除正负方向的最大值后，糙米沿X轴平均运动速度大部分集中在-20～20 mm/s，重力作用的影响相比沿Z轴方向更小，并且沿X轴糙米的运动速度更趋于稳定。通过矢量计算得到糙米沿X轴平均速度为-0.6 mm/s，说明糙米在正六边形米筛中沿X轴正、负两个方向的运动能力基本一致。

图6 糙米沿X轴方向运动速度-时间变化Fig.6 Variation of speed and time of brown rice in the X-axis direction

图7是糙米在不同边数米筛中沿X轴方向的运动速度。糙米沿X轴的平均运动速度随米筛边数的增加呈线性减小，说明随着米筛边数的增加会导致糙米在碾白室内沿X轴的运动能力降低，其中沿X轴运动速度最小的是四边形米筛，即轴筛间隙过小会造成糙米沿X轴的运动能力偏低，导致糙米在碾白室内碾磨不充分。

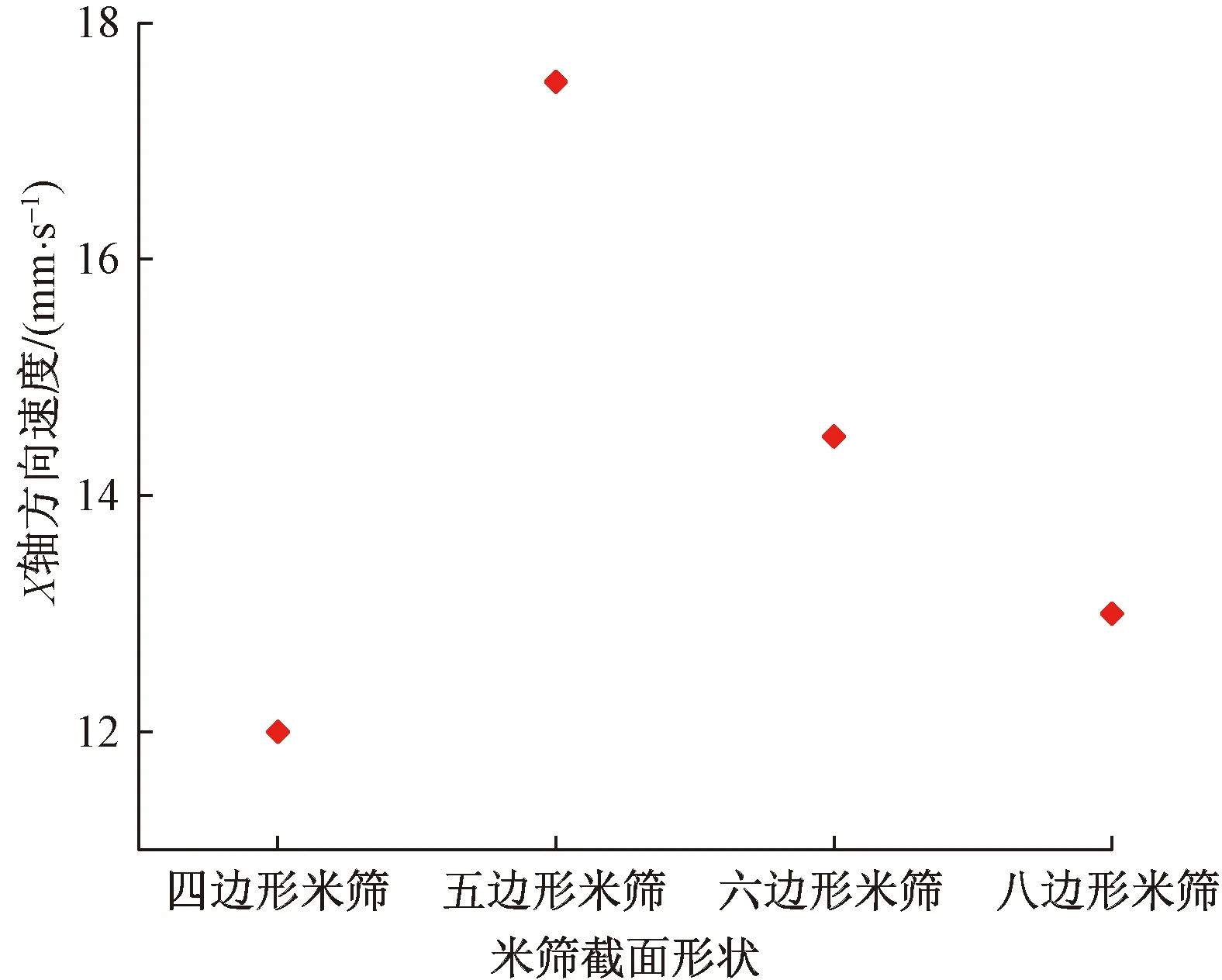
图7 糙米沿X轴的平均速度Fig.7 The average speed of brown rice along the X-axis

3.1.2 糙米翻滚运动分析

糙米的自转角速度大小表现为在碾白过程中糙米翻滚运动的强弱，糙米之间自转角速度的不同会发生相互摩擦，若糙米角速度较低时糙米的两侧发生过碾造成糙米腹背部得不到充分碾磨，造成糙米“发花”现象[12]，直接影响成品米的品质，过强的翻滚运动会造成糙米之间的过度摩擦，降低出米率。

如图8所示，初始阶段糙米的自转角速度保持平稳，糙米的自转角速度随碾白室内糙米数量的增加呈直线增长。

图8 碾白室内糙米自转角速度-时间变化Fig.8 Rotation angular velocity-time variation of brown rice in whitened indoor

将糙米稳定运行时的自转角速度代表糙米在碾白室内的平均角速度[11]。图9是糙米在不同边数米筛中自转角速度变化情况，糙米的自转角速度随米筛边数的增加而逐渐下降，糙米的翻滚能力随自转角速度的降低而降低。对比正四边形、五边形米筛可以得出过小的轴筛间隙会降低米粒翻滚能力。轴筛最宽、最窄距离之间的差值随着米筛边数的增加而减小，米筛转角处阻塞糙米翻滚运动的现象明显减弱，且米筛转角处与糙米发生碰撞的次数降低，严重削减了糙米在碾白室内的翻滚能力。

图9 糙米平均角速度变化情况Fig.9 Variation of average angular velocity of brown rice

3.1.3 糙米碾白压力分析

图10为六边形米筛中糙米在碾白室内碾白压力变化情况。开始阶段糙米未进入到碾白室，糙米受到的压力接近于零，随着糙米逐渐落入碾白室，在碾辊的带动下糙米在碾白室内旋转并与米筛发生碰撞，糙米受到的压力逐渐上升，在1.35 s后糙米所受碾白压力上下波动，然而在2.6 s处糙米的碾白压力发生突变。结合图4和图6糙米在碾白室径向的运动情况来看，在1.35 s后，糙米在X轴、Z轴方向的运动呈现持续的波动状态，说明糙米已经大量堆积在米筛边缘，糙米所受的碾白压力也呈现持续波动状态，与其运动状态规律基本一致。至于2.6 s处糙米碾白压力发生突变可能是堆积的糙米堵塞产生的瞬时压力。

图10 糙米所受压力-时间变化Fig.10 Pressure and time variation of brown rice

图11显示了糙米在不同边数米筛中平均碾白压力变化，在4种米筛中糙米所受到的碾白压力最大的是四边形米筛，根据四边形米筛的外形特征，过小的轴筛距离会降低糙米在碾白室内的运动能力，且在米筛转角发生严重堆积现象，堆积的糙米内层与外层无法充分易位，外层的糙米持续与米筛磨削，导致大部分外层的糙米过碾，而大部分内层的糙米则得不到碾磨，造成糙米碾磨不充分。

图11 不同米筛中糙米的平均碾白压力Fig.11 Average white milling pressure of brown rice in different rice sieves

对比正五边形、六边形和八边形米筛发现，当增加米筛边数时，碾白室内糙米受到的碾白压力逐渐降低。从图5、图7和图9中糙米的运动情况来看，当增加米筛边数，降减了碾白室内糙米的运动能力，米粒之间的碰撞和摩擦能力减小，所以米筛边数增加，糙米受到的碾白压力降低。

3.1.4 糙米破碎分析

图12显示了米筛边数变化后，整个模拟过程中糙米黏结模型的粘接键数量随时间的变化。在0.2 s前未形成粘接键，0.2 s后粘接键的数目发生剧增，主要由于EDEM软件在生成颗粒时需要由大颗粒分裂形成小颗粒再生成粘接键，在0～0.2 s正是此操作的反应时间，而粘接键几乎是瞬间生成，才会有粘接键数量的剧增。随时间的变化，在0.5～1.5 s内损失的黏接键数量较少，在1.5 s之后损失的粘接键数量快速增加。本文中碎米率用断裂的粘接键数量与粘接键总数的比值来表示，即

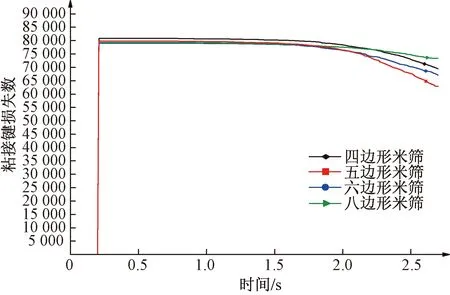
图12 粘接键数量-时间变化Fig.12 Number of bonding keys and time variation

(2)

式(2)中：Sn为n边形米筛碎米率；N为断裂的粘接键数；Na为粘接键总数。

进行四边形米筛模拟仿真实验时粘接键共计生成80 795个，断裂11 389个，根据式(2)，计算得到四边形米筛碎米率S4=14.1%。同理，可得出其他边数米筛碎米率分别为S5=19.8%、S6=15.2%、S8=8.1%。

对比糙米在不同米筛中的碎米率发现，正五边形米筛碎米率最高，而正八边形米筛最低。如图5、图7和图9所示，糙米在正五边形米筛中的运动能力较其他两种米筛高，大量糙米沿X轴正负两个方向堆积于米筛边缘处，沿Z轴负方向堆积于米筛底部，糙米与米筛持续磨削，大部分糙米过碾导致碎米率最高；糙米在正八边形米筛中，运动能力最弱，糙米与米筛之间的磨削大幅度下降，大部分糙米轻碾甚至未与米筛产生磨削，导致八边形米筛碎米率最低。四边形米筛碎米率低于六边形米筛和五边形米筛，主要原因是正四边形米筛碾白室内部空间较小，糙米沿X轴和Z轴方向运动能力差，一小部分糙米与米筛产生磨削，且糙米在正四边形米筛内的易位翻滚能力较弱，导致正四边形米筛的碎米率较低而受到的压力却最高。

3.2 碾辊结构改变对糙米运动及破碎的影响

3.2.1 糙米径向运动分析

图13为改变碾辊结构后糙米在碾白室内沿Z轴运动的平均运动速度变化关系，可以看出改变某一碾辊结辊之后与初始结构糙米沿Z轴方向的运动并未发生太大的变化，糙米沿Z轴方向运动的速度保持稳定状态。

图13 糙米沿Z轴的平均速度Fig.13 Average speed of brown rice along the Z-axis

图14为改变碾辊结构后糙米在碾白室内沿X轴方向运动的平均速度变化趋势。从图14中分析发现，通过增加碾筋高度、减小碾辊直径与增加碾筋个数能增强糙米沿X轴方向运动速度，而增加碾筋个数能够增加糙米与碾筋接触的次数，显著增强糙米沿X轴的运动能力。

图14 糙米沿X轴的平均速度Fig.14 Average speed of brown rice along the X-axis

3.2.2 糙米翻滚运动分析

为了提高烟支重量测量的准确性，必须保证在一支烟上有足够的采样点，才能计算得到烟支的总重量以及烟支重量分布情况，控制系统使用编码器获取同步信号，准确计算烟支重量。

图15是改变碾辊结构后，糙米在碾白室内翻滚运动情况。结果表明糙米的角速度随着碾筋高度的增加、碾辊直径的减小及增加碾筋的个数逐次增加，且增幅较大，糙米自转角速度增幅最大的是增加碾筋个数。其原因在于增加碾筋的高度和个数之后，能够促使糙米在碾白室内获得动力变得更加活跃，增强米粒之间的碰撞、摩擦和翻滚。减少碾辊直径变相增加了碾白室内糙米的运动范围，增加碾筋高度和数目会减小碾白室内的空腔容积，但碾筋高度增加对糙米运动能力的增强效果远大于糙米运动范围减小对其运动能力的减弱。

图15 糙米平均自转角速度Fig.15 Average rotation angular velocity of brown rice

3.2.3 糙米碾白压力分析

图16是改变碾辊结构后，糙米在碾白室内的碾白压力，可以看出增加碾筋高度、减小碾辊直径及增加碾筋个数都能够增加糙米在碾白室内的平均碾白压力，其中增加碾筋个数能够明显增加糙米的碾白压力，主要因为碾筋个数的增加使得碾白室内空间布局发生改变，使得糙米能够充分与碾筋接触，获得更大的碾白压力。

图16 糙米平均碾白压力Fig.16 Average grinding pressure of brown rice

3.2.4 糙米破碎分析

图17所示为改变碾白室结构后糙米黏结模型粘接键剩余数目随时间变化的情况。由式(2)可得S碾辊直径=16.8%，S碾筋高度=30.2%，S碾筋个数=39.7%。

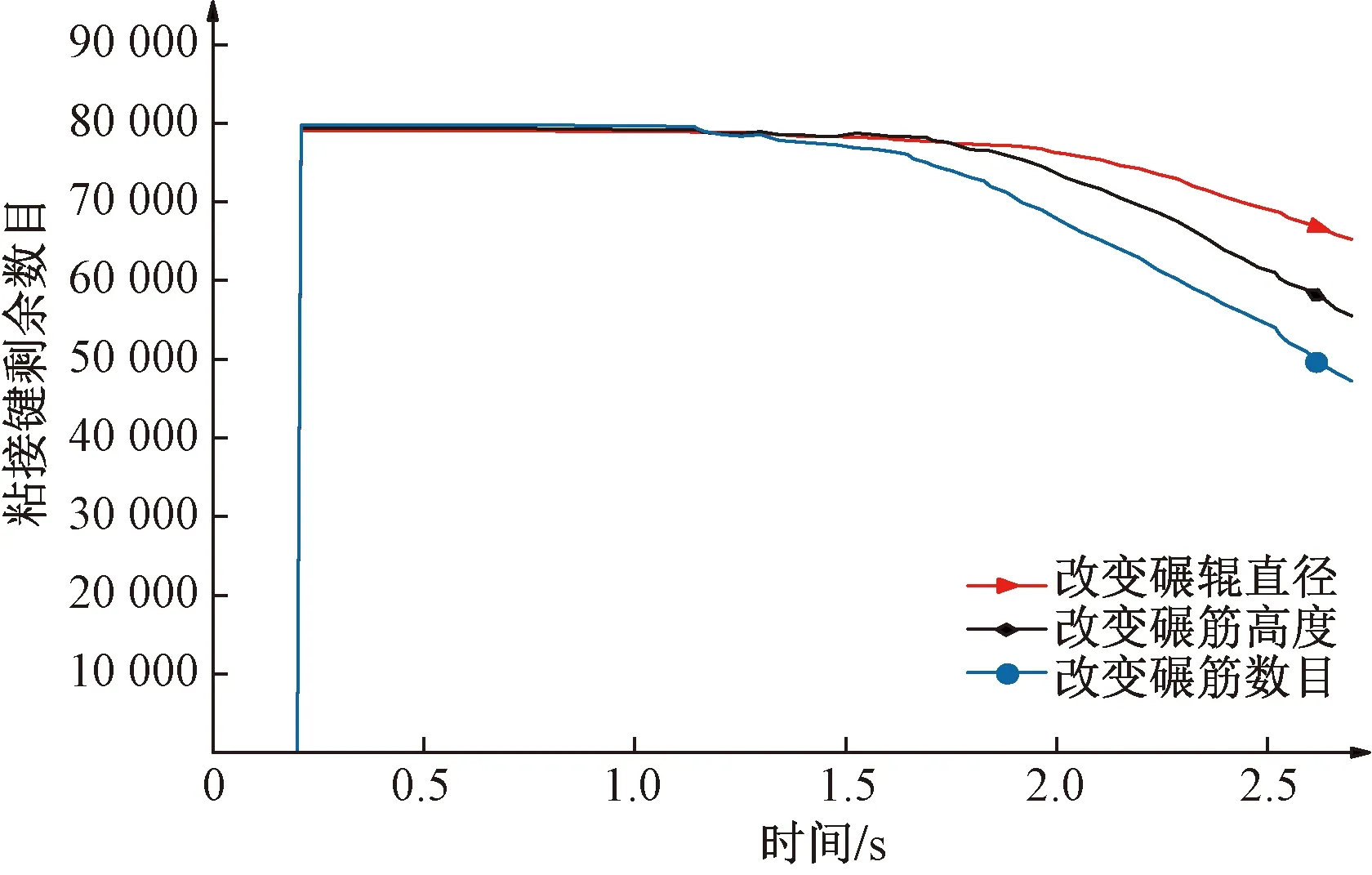
图17 粘接键剩余数目Fig.17 Remaining number of bonding keys

对比改变碾辊结构对碎米率的影响发现，增加碾筋数目碎米率最高，然而减少碾辊直径碎米率最低。前者的主要原因是改变碾辊结构对糙米沿Z轴的运动速度的影响并不明显，但碾筋个数增加后，糙米在碾白室内沿X轴方向的运动速度明显增加，同时糙米在碾白室的自转角速度也明显提高，使得糙米大量堆积于米筛边缘，由于糙米的自转角速度很大，糙米与米筛、碾筋磨削作用加强，导致糙米产生过碾，碎米率增大。而后者的主要原因是减少碾辊直径后，增大了碾白室的轴筛间隙，使得糙米在碾白室内的运动空间变大，即使糙米在米筛边缘处堆积磨削，但是有足够的空间使得糙米进行易位，让更多的糙米与米筛产生磨削，使得糙米的碾白均匀而不过碾；虽然减少碾辊直径后糙米在碾白室内的沿X轴方向运动(图14)和翻滚运动能力(图15)比增加碾筋高度和初始结构的运动能力有所增强，但是增强效果比增加碾筋数目的效果弱，而减少碾辊直径后，糙米在碾白室的碾白压力比增加碾筋高度和碾筋个数都小(图16)，这些因素综合作用下导致减小碾辊直径，糙米碾白的碎米率最低。

4 结论

糙米破碎影响因素很多，其中碾白室结构对糙米碾白运动有重要影响，通过基于离散元技术的糙米的碾白过程模拟及破碎影响分析，发现了以下糙米的碾白运动和破碎影响规律。

(1)米筛边数对糙米碾白运动和碎米率影响规律为：正四边形米筛碾白室内部空间较小，糙米沿米筛径向方向运动能力差，易位翻滚能力较弱，导致碎米率较低而碾白压力却最高；正五边形米筛中的糙米运动能力与受力均较正六边形和正八边形米筛高，大量糙米在正五边形米筛内堆积于米筛边缘和底部，大部分糙米发生过碾的现象导致碎米率最高；糙米在正八边形米筛中，运动能力最弱，糙米与米筛之间的磨削大幅度下降，大部分糙米轻碾甚至未与米筛发生磨削，导致八边形米筛碎米率最低。

(2)改变碾辊结构对糙米碾白运动和碎米率影响规律为：增加碾筋个数使糙米在碾白室内沿径向方向的运动速度和自转角速度明显增加，使得糙米大量堆积于米筛边缘处，糙米与米筛、碾筋磨削作用加强，糙米产生过碾，碎米率增大；减少碾辊直径后，增大了碾白室的轴筛间隙，糙米在碾白室内的运动空间变大，即使糙米在米筛边缘处堆积磨削，也有足够的空间易位，让更多的糙米与米筛产生磨削，糙米碾白均匀而不过碾；另外，减少碾辊直径后糙米在碾白室内的沿径向运动速度和翻滚运动能力比增加碾筋高度的运动能力有所增强，但是增强效果比增加碾筋数目的效果弱，而减少碾辊直径后，糙米在碾白室的碾白压力比增加碾筋高度和碾筋个数都小，糙米碾白的碎米率较低。