钢管约束钢筋混凝土柱抗震设计方法及塑性铰

石若利, 罗靓, 潘志成, 张军, 孙志颖, 顾淑娴, 李其伦

1.云南大学 建筑与规划学院, 云南 昆明650504; 2.南昌航空大学 土木建筑学院, 江西 南昌330063;3.中国水利水电第八工程局有限公司, 湖南 长沙410000

我国建筑产业规模大，但节能减排、人居环境改善、工程效率及品质等问题显现，总体科技贡献率不高。为改善上述落后局面，早在2014年《国家新型城镇化规划(2014～2020年)》明确提出“强力推进建筑工业化”。主要要求包括：采用先进、适用的技术和工艺，减少繁重复杂的手工劳动和湿作业。本质是：应选用合适的结构形式，满足建筑需求，减少施工工序和人工损耗，节约时间和成本。

在高层建筑中，钢筋混凝土柱承受的竖向荷载较大，使得轴压比较高，此时柱的延性明显变差进而导致结构的整体抗震能力变差且易于破坏。周绪红等[1]从构造出发，提出了一种钢管约束钢筋混凝土柱，并开展了5根柱子的低周往复试验研究，结果表明：即使轴压比高达0.8，外钢管对混凝土约束较好，混凝土没有发生压溃剥落，柱的承载力和位移延性系数显著提高24.2%，142.8%。该类柱子的优势在于：①钢管对核心混凝土的约束作用，可有效提高混凝土的抗压强度，从而提高承载力，内填核心混凝土的支撑作用又可以有效地减缓钢管的局部屈曲，提高柱的延性；②外部钢管相当于模板，可承担施工期间的结构重量与外荷载，有效节省了支模、拆模的材料和人工费用，通常通过加强环板与钢梁或钢-混凝土组合梁进行螺栓连接或者焊接，可满足“建筑工业化”的要求。由于该类柱子在实际轴压比高达0.8时仍具有良好的抗震性能，且配置外钢管的工艺简单，不需支模，操作便利，外观整洁，因此有必要在试验验证的基础上对该类柱进行精细化有限元分析，深入研究其抗震设计方法及塑性铰计算方法。

地震作用下，框架柱端部较大弯矩处产生较大的塑性变形，成为塑性铰。在框架结构设计时，应加强柱端的塑性铰区域约束，使其具有较好的转动能力，从而提高结构的抗震性能。很多学者通过试验研究、数值模拟和数据回归等方法，分析了钢筋混凝土柱塑性铰长度的影响因素，提出了不同的塑性铰长度(plastic hinge length)Lp计算公式。邵长江等[2]设计了7个矩形钢筋混凝土桥墩柱进行低周往复试验，结果表明塑性铰长度随墩高L、配箍率ρsv的增大而增大，而纵筋配筋率ρs的影响较小。王斌等[3]对带型钢的钢筋混凝土框架柱进行拟静力试验，根据柱的破坏形态，指出塑性铰长度随纵筋配筋率ρs、型钢率ρ、钢筋屈服强度fy的增大而增大。周建等[4]采用OPENSEES软件对72个桥墩进行横向推覆数值模拟，发现塑性铰长度与墩高L、纵筋配筋率ρs和截面高度B有关。孙治国等[5]对154根钢筋混凝土墩柱抗震试验结果进行回归，认为塑性铰长度与纵筋屈服强度无直接关系，提出公式Lp=0.1L+7.32ds-0.165B，L为柱长，ds为受力纵筋的直径，B为截面高度。王震等[6]通过回归48根桥墩柱的滞回试验结果，指出塑性铰长度随柱高L、截面宽高B、纵筋配筋率ρs和纵筋屈服强度fy的增大而增大。以上研究认为柱长对塑性铰长度影响较大，而纵筋配筋率、纵筋屈服强度、配箍率以及截面尺寸的影响系数差异大，且未考虑轴压比的影响。Sheikh等[7]认为高轴压比下钢筋混凝土柱沿全长被压碎时，塑性铰长度Lp为1.0L。仇建磊等[8]根据30个压弯破坏柱的试验结果，指出轴压比n、配筋率ρs都会影响钢筋混凝土柱的塑性铰长度。袁方等[9-10]指出柱的塑性铰长度随轴压比n、柱长L增大而增大，随配箍率增大而减小。以上都是普通钢筋混凝土柱塑性铰的研究成果，而对于钢管约束钢筋混凝土柱塑性铰的研究涉及较少。

以往钢筋混凝土柱抗震性能的有限元分析中，主要采用弹塑性本构模型，没有考虑往复荷载下混凝土的塑性损伤特性和钢材的硬化特征，导致有限元结果不够准确。为此，笔者主要开展如下工作：①采用ABAQUS有限元软件建立拟静力荷载作用下钢管约束钢筋混凝土柱的三维实体精细有限元模型，模型考虑往复荷载作用下混凝土的塑性损伤特征与钢材的混合强化特征以及钢管对混凝土的约束作用，与拟静力试验结果[1]对比验证模型的正确性；②建立136个钢管约束钢筋混凝土柱足尺有限元模型，开展不同参数下柱的滞回性能分析，探讨钢管厚度对承载力和延性的影响，提出不同轴压比下钢管厚度、套箍系数等抗震设计方法、柱的塑性铰判定方法及长度计算公式。

1 试验验证

1.1 试验简介

图1 试件示意图

1.2 建模方法

混凝土采用塑性-损伤本构模型,基本参数设置见表1。骨架曲线按丁发兴等[11]提出的应力-应变关系统一计算如(1)式所示,式中的参数见表2;损伤变量采用丁发兴等[12]提出的基于弹性模量损伤的计算值,受压刚度复原因子Wc取0.8,受拉刚度复原因子Wt取0.2。

(1)

纵筋、箍筋、钢管和盖板均为钢材,本构关系采用丁发兴等[12]提出的ABAQUS中参数表示的混合强化模型,以反映钢材的屈服面及包辛格效应。模型的6个参数见表3,考虑到钢管容易曲屈导致硬化特征将变得不明显,随动硬化参数(kinematic hard parameter)C1取文献[12]的1/10,即为750。

表1 ABAQUS软件中混凝土的基本参数取值

表2 ABAQUS软件中混凝土的骨架曲线参数取值

注:大部分参数可由立方体抗压强度fcu直接算出;钢管约束混凝土柱为三轴受压,普通混凝土柱为单轴受压。

表3 AUAQUS有限元软件中钢材相关参数取值

模型的界面接触设置为:①纵筋与箍筋合并(merge)后,内置(embedded region)于核心混凝土;②钢管与核心混凝土之间设置库伦摩擦型接触,由切线方向的摩擦和法线方向的硬接触构成,摩擦因数取0.5;③盖板与柱顶采用绑定的约束方式(tie)。采用与拟静力试验一致的边界条件:试件嵌固在刚性混凝土底座上,故对柱底完全固定,X,Y,Z3个方向的位移和转角均设置为0°。加载方式也与试验相同,共设置2个分析步,分析步类型均为静力通用,包括:①第1个分析步,将恒定轴压力以压强(轴压力/盖板面积)的形式施加在柱顶盖板表面,施加时间为1 s,并传递到第2个分析步;②第2个分析步,对柱顶施加水平往复位移。单元及网格见表4,有限元模型如图2所示。

表4 单元类型和网格划分技术

图2 钢管约束钢筋混凝土柱的有限元模型

1.3 模型验证

将2个典型试件(SRC-60、STRC-60-8)的破坏形态和曲线结果对比如图3至4所示,图中“S”表示方形截面(square),“T”表示钢管约束(steel tube confined),RC为钢筋混凝土(reinforced concrete),60为混凝土强度等级,n为轴压比。B,L,t分别为截面边长、柱长、钢管壁厚。可知:①普通钢筋混凝土柱SRC-60的最大应力区域主要位于上下两端范围,与试验现象“两端弯矩最大处混凝土严重压溃,且纵筋压屈”吻合,配置外部约束钢管后,STRC-60-8的鼓曲程度减小,压溃现象不明显,纵筋没有失稳;②有限元荷载-位移滞回曲线比试验曲线略饱满,但整体变化趋势一致,且有限元荷载-位移骨架曲线与试验曲线吻合良好,因此建立的有限元模型具有较高的精度和可行性。

图3 普通SRC-60破坏形态、滞回曲线、骨架曲线比较(n=0.8,B×L=200 mm×1 200 mm)

图4 带钢管STRC-60-8破坏形态、滞回曲线、骨架曲线比较(n=0.8,B×L×t=200 mm×1 200 mm×2.66 mm)

2 参数分析

2.1 足尺模型

设计并建立了10个普通钢筋混凝土柱和126个钢管约束混凝土柱的三维实体精细有限元足尺模型算例开展拟静力分析,截面均为B×D=500 mm×500 mm,柱长均为L=2 000 mm。编号中第1个字母“s”表示方形(square),第2个字母“c”表示柱子(column),第3个字母“h”表示受荷模式为滞回(hysteresis)。材料性能为:①混凝土为C40、C60和C80,立方体抗压强度fcu为40,60,80 MPa,对应的轴心抗压强度fc分别为29.6,47.5,66.4 MPa;②钢管为Q235,Q345,Q420,屈服强度fy为235,345,420 MPa,厚度t=3,4,6,8,10 mm,定义钢管的套箍系数为ξ=fyAs/fcAc[13];③纵筋为HRB400,屈服强度fy为400 MPa,直径ds为20 mm,横向间距as为150 mm,箍筋为HPB300,屈服强度fyv为300 MPa,直径dsv为10 mm,纵向间距bs为100 mm。足尺模型算例的具体参数见表5,有限元模型如图5所示,水平往复加载制度按《建筑抗震试验规程JGJ/T101-2015》[14]统一为(5, 10, 15～40,45,50,60,70,80,90,100)mm,50 mm之前以5 mm为增量步,50 mm之后以10 mm为增量步,施加时间为60 s。

图5 足尺有限元模型

表5 钢管约束钢筋混凝土柱足尺模型算例参数

2.2 钢管的影响

以方形普通钢筋混凝土柱sch1～10和厚度t=3 mm的方钢管约束钢筋混凝土柱sch10～20足尺模型算例的滞回性能计算结果为例,典型轴压比(n=0.5,0.8,1.0)的有限元荷载-位移滞回曲线如图6所示,不同轴压比的极限承载力和破坏位移比较见图7,破坏位移按《建筑抗震设计规范GB50011-2010》[15]取水平力下降到极限承载力85%时对应的位移,破坏位移角按(2)式计算:

破坏位移角=破坏位移/柱长L

(2)

式中，柱长L取2 000 mm。如果水平位移加载到100 mm时,水平力仍没有下降到极限承载力的85%,则取100 mm为破坏位移。从图6至7可知:

图6 典型轴压比下柱的滞回曲线

图7 钢管对柱极限承载力和破坏位移角的影响

1) 相同轴压比时,钢管约束钢筋混凝土柱的滞回曲线比普通钢筋混凝土柱更饱满,极限承载力更大,下降更缓慢,延性更好;

2) 当轴压比增大,2种柱的极限承载力都呈增大趋势,两者分别在轴压比n=0.8,n=0.9时达到极限承载力的最大值,但轴压比增大会使得滞回曲线下降更快,延性明显变差;

3) 对于普通钢筋混凝土柱,当轴压比≤0.4时,破坏位移角都大于规范限值1/50[15],当轴压比达到0.5时,滞回曲线出现明显的下降段,且破坏位移角小于规范限值1/50,当轴压比达到0.8,1.0时,混凝土迅速压溃而丧失承载力,滞回环过了第3象限后直接回到原点,延性很差;

4) 对于钢管约束钢筋混凝土柱,其破坏位移角普遍大于规范限值1/50,只有当n=1.0时破坏位移角小于1/50,此时可略微增大钢管厚度。

轴压比为0.5，0.8，1.0时2种柱的核心混凝土控制点纵向应力-纵向应变曲线如图8所示,可见:①由于外部钢管分担了混凝土承担的轴压力,以及钢管对混凝土的套箍约束作用,混凝土的压应变明显减小,且套箍约束作用使得混凝土的压应力显著提高,随着轴压比增大这种约束作用更明显;②加载后期三者的应力-应变曲线斜率变小,表明塑性损伤使得弹性模量和刚度都减小。

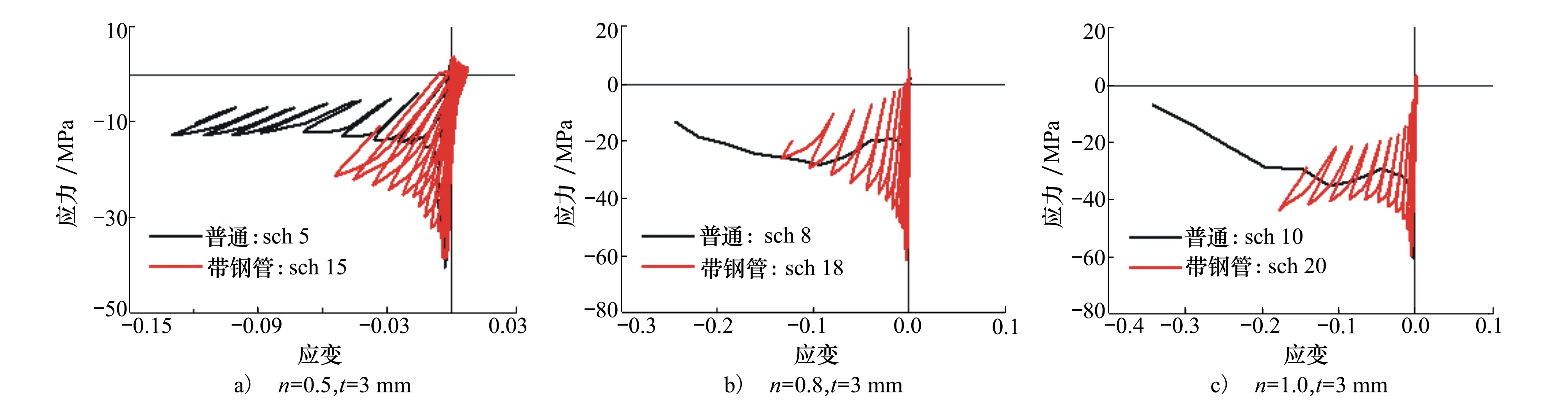
图8 混凝土控制点的应力-应变滞回曲线

轴压比为0.5,0.8,1.0时2种柱的纵筋、箍筋控制点应力-纵向应变曲线如图9至10所示。当轴压比n≤0.5时,纵筋应变为拉压往复趋势,高轴压比作用下,纵筋应变以压应变为主。箍筋的作用是约束柱的侧向膨胀变形,以拉应变为主。可见:①钢管的套箍约束作用使得混凝土压应变减小,故混凝土内部纵筋的压应变也明显减小,但纵筯的压应力峰值接近，钢管约束了柱的侧向变形,分担了箍筋的一部分约束作用,因此箍筋的拉应变也显著减小,但箍筯的拉应力峰值接近;②当n=0.5时,普通柱的纵筋压应变、箍筋拉应变为0.157、0.063,钢管约束钢筋混凝土柱的纵筋压应变、箍筋拉应变减小为0.053,0.054,减小了66.2%,14.0%;③高轴压比0.8和1.0作用时,普通钢筋混凝土柱迅速压溃,纵筋压屈,压应变为0.772,0.763,箍筋拉断,拉应变为0.103,0.282,而钢管约束钢筋混凝土柱的纵筋压应变减小为0.144,0.200,分别减小了81.3%,73.9%,箍筋拉应变减小为0.067,0.082,分别减小了35.2%,70.9%。

图9 纵筋控制点的应力-应变滞回曲线

图10 箍筋控制点的应力-应变滞回曲线

3 抗震设计方法

为确定不同轴压比时方钢管约束钢筋混凝土柱的合理钢管厚度和套箍系数,优化分析Q345+C40,Q235+C40,Q345+C60,Q345+C80,Q420+C80这5种匹配,对比了136个足尺模型算例的滞回性能,其中钢管厚度为3,4,5,6,8,10 mm且通长布置,轴压比为0.2,0.5,0.8和1.0。以Q345+C40为例,计算得到不同钢管厚度时STRC柱的破坏位移角、极限承载力以及极限承载力提高率见图11,可知:STRC柱的破坏位移角和极限承载力随钢管厚度增大而明显增大,定义STRC柱的破坏位移角达到位移角限值1/50[15]时的钢管厚度为合理钢管厚度。不同轴压比下STRC柱的合理钢管厚度及套箍系数见表6,可见当轴压比为0.2时,不需要配置钢管,破坏位移角可达到0.04,已超过位移角限值1/50,满足规范要求,当轴压比为0.5,0.8,1.0时,合理套箍系数分别为0.10,0.26,0.40。

图11 不同钢管厚度对柱抗震性能的影响

表6 合理钢管厚度和套箍系数

4 塑性铰定义及长度计算公式

4.1 塑性铰定义

当方形STRC柱滞回曲线达到正、负峰值荷载时,柱底部形成塑性铰,之后水平荷载逐渐减小。此时136个足尺模型的混凝土纵向应变与峰值应变以及钢管应变与屈服应变比值的分布规律如图12所示,其中sch1～10为普通钢筋混凝土柱,未配置钢管,故图12b)没有前10个数据点。由图12可知:

图12 正、负峰值荷载时136个足尺模型的纵向应变规律

1) 按混凝土应变考虑,混凝土的纵向受拉应变、受压应变与其峰值应变的比值在2,3附近波动,因此混凝土纵向受拉、受压应变达到2,3倍峰值应变时,柱底部分别形成拉铰、压铰;

2) 按钢材应变考虑,在实际的操作过程中,钢管的应变较易量测,打磨钢管外表面后粘贴应变花,通过电导线连接到应变仪即可读取数据;而量测纵筋和箍筋的应变较困难,需对混凝土打孔,会削弱柱的抗震性能,故选取钢管应变作为塑性铰出现的判定依据更实用,钢管的纵向受拉应变、受压应变达到1.5倍、4倍屈服应变时,柱底分别形成拉铰、压铰。

4.2 塑性铰长度计算公式

按4.1节,加载结束后混凝土纵向压应变大于3倍峰值应变的区域长度即为塑性铰长度。轴压比0.2,0.4,0.6,0.8,1.0下,5个普通钢筋混凝土柱和5个钢管约束钢筋混凝土柱的塑性铰长度(彩色区域)见图13至14,可知:①小轴压比作用时,塑性铰长度较小;②高轴压比0.8和1.0作用时,普通钢筋混凝土柱完全压屈,塑性铰长度为全长2 000 mm,而设置外钢管可有效减小柱端塑性铰长度,塑性铰长度控制在1 400,1 600 mm。

图13 不同轴压比下普通钢筋混凝土柱的塑性铰区域

图14 不同轴压比下钢管(t=3 mm)约束混凝土柱的塑性铰区域

根据136个足尺模型算例的有限元塑性铰长度数据,考虑轴压比n和钢管的套箍系数ξ,笔者建议塑性铰长度Lp计算公式为

Lp=βL=(1.12n-0.20ξ-0.65nξ)L

(3)

式中，β应满足0≤β≤1,当β<0,取β=0,此时塑性铰长度为0,当β>1,取β=1,此时塑性铰长度为柱全长。由(3)式可知:塑性铰长度随轴压比增大而增大,随钢管套箍系数增大而减小。按(3)式计算所得塑性铰长度与有限元塑性铰长度对比如图15所示,两者比值的均值为1.018,离散系数为0.021,表明(3)式的精度较高。

图15 塑性铰长度的解析计算与有限元模拟结果对比

5 结 论

基于混凝土三轴塑性-损伤模型和钢材混合强化模型,采用ABAQUS软件建立方钢管约束钢筋混凝土柱的试验缩尺模型和足尺模型进行拟静力分析,通过试验验证和参数分析,结论如下:

1) 拟静力荷载下方钢管约束钢筋混凝土柱的破坏形态、荷载-位移滞回曲线和荷载-位移骨架曲线有限元计算结果与已有拟静力试验结果吻合良好,表明建立的有限元模型可准确模拟方钢管约束钢筋混凝土柱的滞回性能;

2) 钢管的套箍约束作用可有效减小混凝土的压应变峰值和提高压应力峰值,显著减小纵筋和箍筋的应变,从而延缓柱的破坏,提高承载力和延性;

3) 提出了各钢管与核心混凝土强度等级匹配、不同轴压比下的合理钢管厚度等抗震设计方法,当轴压比0.2,0.5,0.8,1.0作用时,合理的钢管套箍系数分别为0,0.10,0.26,0.40;

4) 对于长宽比不大于8的短柱和中长柱,当混凝土纵向受拉、受压应变达到2,3倍峰值应变时,或外钢管的纵向受拉应变、受压应变分别达到1.5倍、4倍屈服应变时,柱底形成拉铰、压铰,外钢管可有效减小柱端塑性铰长度,提出了反映轴压比和套箍系数2个参数影响的塑性铰长度公式,精度较高,可用于实际工程。