基于神经网络的电力用户行为预测

汤铭，丁一新，王凌，程昕云，肖茂然，李乃昊

（1.国网江苏省电力有限公司信息通信分公司，南京 210024；2.国网电力科学研究院有限公司，南京 210037）

0 引言

随着电力负荷种类的日益增多，电网难以单独与用户进行交易，而单一的用户也难以满足电网的要求［1-2］。大部分需求响应中的负荷预测侧重于对用户负载的预测，缺乏对用户在LA 模式下的行为的不确定性预测［3］。本文分析了LA 模式下有关DR 原理，然后阐述LSTM 算法的典型特点，提出了基于LSTM 的用户响应行为识别方法。最后通过算例分析，验证了该方法能够准确预测用户的响应行为。

1 现状分析

负荷聚合商模式下的需求响应实现过程如图1所示，负荷聚合商模式包含3大因素，分别是电力企业、负荷聚合商和可参与需求响应的用户［4-5］。其运行模式为：电力企业与负荷聚合商提前设定价格并签订合同，电力企业依据自身运行情况判断是否需要用户侧参与调节，若需要则提前向负荷聚合商下发负荷调节量指标。由于不同用户参与电网调节的成本各不相同，负荷聚合商根据自身利益调节各类负荷并给与相应的补贴［6-8］。

图1 需求响应示意图

在基于激励的需求响应场景下，用户对不同激励的响应受到多种因素的影响，主要包含以下几个因素［9-10］：备选方案的可用性、用户的当前负载状态、用电支出占总支出的比例、外部环境等。

2 基于LSTM的行为预测

2.1 LSTM模型

对于LSTM 网络，它们输入的影响因素越多，其预测结果越准确。基于LSTM 模型的输入量如下：最大负荷、最小负荷、时间、当前收到的激励［11］。图2为典型LSTM的结构。

图2 LSTM网络结构

在LSTM 结构中，遗忘门决定何种信息被保留［15-17］。遗忘门读取上一时刻的状态信息ht-1和当前时刻的输入信息xt，然后向细胞输出0至1位数字，当输出值为0，将丢弃所有信息，当输出值为1，将保留所有信息。细胞中存储的信息是前一次的状态信息，根据遗忘门的输入，只保留有用的信息。遗忘门更新公式见式（1）。

式中，σ表示信号函数，Wf代表特征加权，bf代表遗忘门的偏移数据，ht-1表示前一个时间段的输出数据，xt表示当前时间段的输入数据。

结合信号函数处理生成输入量，同时使用tanh 函数生成候选值向量。输入门更新公式见式（2）和式（3）。

式中，C～t表示一个候选值向量。

细胞记录了上一时刻状态，并基于当前输入数据，更新细胞中的状态信息。细胞格的更新公式见式（4）。

式中，bO是输出门的偏移量。

2.2 行为预测

LSTM 具有记忆功能，能够反映负荷数据在时间顺序上的联系。将LSTM 应用于用户行为预测，其关键问题在于负荷数据的预处理、参数的确定以及解决由于数据杂乱，结构参数多带来的训练困难的问题。针对本文提出的基于LSTM 的用户行为预测，具体步骤如下：

（1）获取数据。输入数据包括最小和最大负荷、平均负荷、相关激励。由于不同的输入数据单位不同，需要进行标准化处理，标准化的公式如下：

（2）初始化参数。结合正态分布特性，进一步初始化数据权重，平均值和标准差分别设置为0和1，所有初始偏置常数设置为0.1。

（3）训练LSTM模型。在模型训练时，结合实际情况采用梯度下降法对参数进行训练，梯度下降法沿着梯度的相反方向以迭代方式更新参数θ。

式中，α表示学习率，LOSS 表示预测值和实际值之间的均方误差。

（4）模型预测。在得到训练模型之后，使用式（1）中的方法输入数据集，通过训练模型实现用户行为预测。

2.3 评价指标

本文结合统计学误差分析与电网数据特点，采用平均误差、均方根误差以及平均绝对百分比误差作为评价指标［12-13］。计算方法分别见式（9）—（11）。

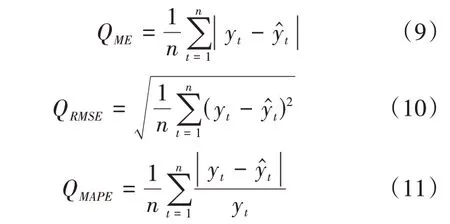
式中，yt表示实际负荷数据，y^t表示预测负荷数据，n为负荷数据数量。

3 实验验证

本文选取国家电网某公司提供的符合数据进行实验验证，数据以15分钟为周期进行采样，共获得96 组12 小时的负荷数据。选择80%的数据用于训练数据集，剩下20%的数据作为测试集进行验证。

本文将所提基于LSTM 模型的预测方法与最小二乘法及k邻近（KNN）预测方法进行对比，如表1所示。

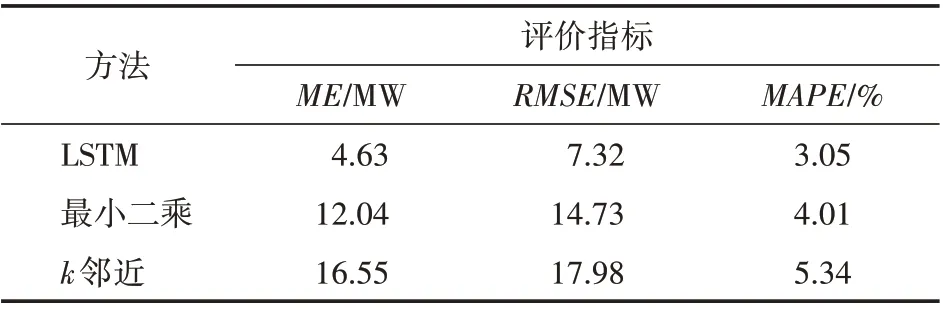
表1 准确率对比

根据表1的数据分析，可知基于LSTM模型的负荷预测方法的ME、RMSE、MAPE 分别为3.83MW、5.12MW、1.08%，平均误差（mean error，ME）相比于最小二乘法低了7.41MW、相比于k邻近预测方法低了11.92MW；均方根误差（root mean square error，RMSE）相比于最小二乘法低了7.41MW、相比于k邻近预测方法低了10.66MW；平均绝对百分比误差（mean absolute percentage error，MAPE）相比于最小二乘法低了0.96%、相比于k邻近预测方法低了2.29%。其模型各项指标都优于最小二乘法及k邻近（KNN）预测方法。

为对比使用基于LSTM 模型的预测方法与最小二乘法及k邻近（KNN）预测方法的预测效果，图3 展示了这三种方法的预测值和真实值之间的差距，相比于其他两种方法，基于LSTM 模型的负荷预测效果更优。

图3 负荷预测结果与真实值对比

4 结语

本文针对目前缺少对于基于激励的需求响应的用户响应行为精准预测，对用户需求响应特征和影响因素进行了深入分析，并对LSTM 神经网络的适用性进行了理论分析。然后提出了基于LSTM 数据驱动的激励型需求响应用户行为预测方法，并通过算例进行验证。通过仿真实验可以看出，与线性回归方法相比，本文提出的算法能够提高单个用户响应行为的预测精度，能够准确预测用户群体的响应行为。本文的工作可以进一步推进需求响应的精细化管理。