求解绝对值方程的改进捕鱼算法
陈建荣,陈建华
(1.右江民族医学院公共卫生与管理学院,百色 533000;2.右江区医疗保障服务中心,百色 533000)
0 引言
关于绝对值方程(absolute value equations,AVEs)的研究主要来源于两个方面[1-3],一是区间线性方程,二是线性互补问题。自Rohn[4]和Mangasarian[5]在绝对值方程相关理论方面做出了开创性的研究工作后,众多学者对绝对值方程开展了较为广泛的研究,并取得了较为丰富的成果[6-10]。张晓敏[6]使用神经网络算法对绝对值方程进行求解。封京梅等人[8]提出了基于单纯性法进行局部优化的人群搜索算法求解绝对值方程。雍龙泉[9]则提出一种五阶牛顿迭代法来获得绝对值方程的解。Dong 等人[10]提出一种求解绝对值方程的新的SOR-like方法。
群智能算法[11]作为演化计算技术的一类,是一种能够解决大多数全局优化问题的有效方法,且因其具有潜在的并行性和分布式特征而得到了广泛的研究和应用[12-13]。采用捕鱼策略的优化算法,即捕鱼算法(fishing algorithm),是陈建荣等人[14]通过观察和模拟渔夫在江面上捕鱼的行为习惯而提出的一种群智能算法,该算法被应用于函数寻优和求解约束优化等问题,并表现出较好的性能[14-16]。
1 问题与转化
一般而言,绝对值方程问题的形式如下[4]:

2 捕鱼算法简介[14]
算法的基本假设包括七方面:一是水中鱼的分布及密度保持不变;二是渔夫在撒网前无法提前知晓水中鱼的分布情况;三是渔夫会朝鱼密度大的方向前进;四是渔夫会停留在鱼密度大的位置撒网捕鱼;五是渔夫通过使用网眼更小的渔网将鱼一网打尽;六是如果当前位置没有鱼或者鱼很少,那么渔夫会移动到别的位置撒网捕鱼;七是渔夫之间避免相互碰撞。
捕鱼算法包括三种基本的搜索方法,即移动搜索、收缩搜索和随机搜索。算法开始时,首先对渔夫群体进行初始化,然后各个渔夫根据自身当前的状态来选择不同的搜索方法进行状态更新,最后在全体渔夫的共同努力下找到鱼密度最高的位置(即问题的最优解)。
3 改进捕鱼算法
3.1 算法参数
改进捕鱼算法在运行前,需要设置的算法参数包括如下六个:最大迭代次数ϑ、群体规模θ、步长τ、收缩系数σ、撒网次数m和阈值ω。此外,为了记录每一次迭代中找到的最优值Z(x*)和对应的最优解x*,算法设置有公告板。
3.2 渔夫个体及目标函数
用n维向量xj=(xj,1,…,xj,k,…,xj,n)T来表示渔夫群体中的第j个个体所处的位置。此外,由(2)得到目标函数为

其中,U=Ax- |x|-b。于是,第j个渔夫所处位置对应的目标函数值为Z(x)j。
3.3 撒网方法与改进
根据分析可知,捕鱼算法的撒网点集中数据点的数量是3n,也就是说,每一个渔夫的撒网点集的规模会随着所求解问题的维数而呈现指数级增长。例如,对于二维的问题,渔夫撒网点的个数是32=9;而当问题的维数变成五维的时候,渔夫撒网点的个数就是35=243;当维数是十维的时候,对应撒网点的个数是310=59049。注意,在撒网点集中的数据点都是向量(一维问题时为标量),因此,对于十维的问题,在算法每一次迭代过程中,至少需要存储59049个十维向量。
此外,由于在每次产生撒网点集之后,需要计算出所有撒网点对应的目标函数值,渔夫才能根据这些结果来选择自己下一步的搜索行为(即选择何种搜索方法)。以上述的十维问题为例,渔夫的撒网点数是59049,那么需要计算这59049个点对应的目标函数的值,也就是需要计算59049 次函数的值。按照渔夫规模θ= 100 计算,每一次迭代就需要计算5904900 次目标函数值。倘若目标函数值的计算相对复杂,则需要消耗大量的运算资源,从而使算法效率大大降低。
为了降低计算机系统内存的使用和减少目标函数的计算次数,受到文献[15]的启发,本文对捕鱼算法的撒网方法进行改进。具体而言,在改进捕鱼算法中,第j个渔夫的撒网点集由下式给出:

其中,j= 1,2,…,θ,rand返回一个在区间(0,1)内均匀分布的随机数。
3.4 程序流程
现将改进捕鱼算法的流程简单描述如下。
输入:最大迭代次数ϑ、群体规模θ、步长τ、收缩系数σ、撒网次数m和阈值ω。
输出:最优值Z(x*)和最优解x*。
(1)对θ个渔夫进行随机初始化;
(2) 如果当前迭代次数已达到最大迭代次数ϑ,算法停止并输出结果,否则转(3);
(3)根据式(3)分别计算出θ个渔夫各自的目标函数值Z(x)j,j=1,2,…,θ;
(4) 根据式(4)产生θ个渔夫的撒网点集,并用式(3)计算出点集中所有的点对应的目标函数值;
(5) 根据下述三条规则依次对θ个渔夫进行状态更新,并转(2)。

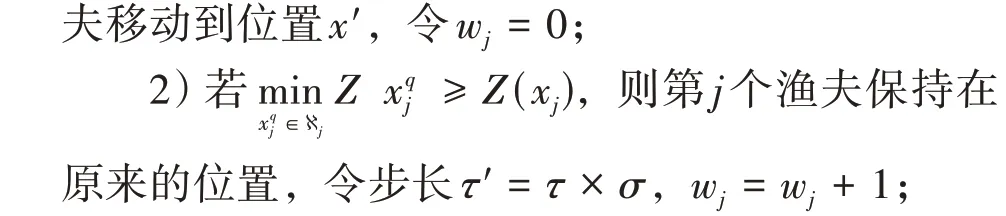
3)若wj≥ω,则对第j个渔夫进行重新随机初始化。
4 数值实验与对比分析
4.1 实验环境与说明
数值实验部分所使用的台式计算机硬件配置为:Inte(lR)Core(TM)i7-4790K CPU@4.00 GHz(睿频4.8 GHz),32 GB 双通道DDR3 2400 MHz 内存;软件环境为:64 位Windows 10 专业版操作系统,MATLAB版本R2020a。
数值实验分为两部分,第一部分是捕鱼算法与改进捕鱼算法求解绝对值方程的结果对比,第二部分是改进捕鱼算法与其他群智能算法的对比。为简单起见,下文中以改进算法指代改进捕鱼算法。
此外,为了能更好地检验算法的性能,在数值实验中采取以下的方法:①在每一次算法开始运行时,均使用MATLAB 中的随机函数对渔夫位置进行随机初始化。②对于每一个算例,算法均独立运行20次,并记录和统计出最后结果。
4.2 结果与分析


(1)捕鱼算法与改进算法性能对比。这里将捕鱼算法和改进算法的参数统一设置为:最大迭代次数ϑ= 800、群体规模θ= 10、步长τ= 0.8、收缩系数σ= 0.8、撒网次数m=27(仅改进算法有此参数)和阈值ω= 10。
两种算法的运行结果如表1 所示。从表中可以看出,在求解维数较低的问题时,如例1 和例2,两种算法的求解效果和精度都很好。但当问题的维数达到十维的时候,如例3(n=10)和例4(n=10),改进算法在最小值、最大值、平均值和方差这四个指标上均比捕鱼算法效果要好。从运行时间上看,改进算法的耗时明显比捕鱼算法要低得多,这说明改进之后算法的计算量有较大幅度的下降,求解问题的速度提高了。值得注意的是,当n=20 时,如例3(n=20)和例4(n=20),因捕鱼算法所需内存容量远大于32 GB 的系统内存而无法运行,所以表1 中未能给出相应的计算结果。然而,改进算法对于求解n=20的问题毫无压力,不仅获得了较高的求解精度,且其运行耗时和低维问题相比并没有显著提高,这说明本文对捕鱼算法的改进是有效的。

表1 捕鱼算法与改进算法结果对比
(2)改进算法与其他群智能算法求解结果对比。不同算法运行结果如表2—表5 所示(“—”表示原文未给出数据)。
从表2—表5中的数据可以看出,对于求解不同维数的绝对值方程问题,从最小值、最大值、平均值和方差这四个指标上看,与粒子群算法、改进粒子群算法、人群搜索算法及其改进算法相比,本文给出的改进算法的求解精度都是最高的,而且算法的稳定性均比其他对比算法要好。此外,从运行时间上看,本文给出的改进算法的运行速度很快,大概只需要0.4 秒即可求得问题的最优解。

表2 不同算法求解例1的结果对比

表3 不同算法求解例2的结果对比

表4 不同算法求解例3(n=20)的结果对比

表5 不同算法求解例4(n=20)的结果对比
5 结语
本文在分析捕鱼算法不足的基础上,通过对渔夫撒网方法的改进,进而给出了一种求解绝对值方程的改进捕鱼算法。改进算法在求解绝对值方程问题时,不仅能获得更快的收敛速度,而且在计算机内存消耗和运行耗时上均比原算法要好。此外,与粒子群算法和人群搜索算法相比,改进算法拥有更好的稳定性和求解精度。未来的研究将针对表达形式更为复杂的高维绝对值问题的求解展开,并在此基础上分析和讨论改进算法的性能特点,以期进一步扩展改进算法的应用范围。

