二方连续云水纹的数学演绎方式

李至惟 张 森

一、云水纹起源

云水纹是一种波状的双线纹，其造型具有一定的流动感。总体来看，云水纹是经过数千年发展而来的一种具有形式美感并被古代工匠艺人普遍采用而成为一种文化符号的中华文明代表性纹样，具有深厚的文化内涵和精神属性。[1]从形态结构上划分，云水纹分为不连续云水纹、二方连续云水纹和四方连续云水纹。不连续云水纹就是重复的云水纹图案之间无法贯通连接；二方连续云水纹的头尾两个方向可以互相连接；四方连续云水纹则是图案的四个方向都可以连接。其中，二方连续云水纹因其对自然形态的表现更加真实，形态更加细长优雅，能表现画面的悠远朦胧感，而被更加广泛地接受和应用。本文重点研究二方连续云水纹的数字化生成方式。

二、云水纹在现代设计中的运用

在现代设计中，云水纹这一古老纹样因其优美的形态、深远的意境感以及极厚重的文化内涵而仍被广泛采用。当今，在壁画、服装、平面、游戏等不同设计领域皆广泛运用云水纹作为视觉元素。

2010年广州亚运会颁奖礼服取名“行云流水”（图1），其以云水纹为主要装饰图案，并结合广州当地特色，运用现代图示语言对传统云水纹纹样进行加工。“行云流水”的设计师——北京服装学院贺阳教授阐述作品设计理念提到：“最终我决定用中国传统云水纹图案，色彩上用岭南画派风格的蓝绿、黄蓝，以体现珠江之水的蓝与广州特有的亚热带地貌以及植物的黄绿色。而色彩间晕染过渡也经过特别处理。我的感受是，云水纹在衣服上特别好运用，云是变幻不定的，可以随意修改，线条也比较好运用。”云水纹在当今社会的另外一个重要的应用领域是包装设计。包装设计师大量采用云水纹对产品包装进行装饰，一方面因为云水纹造型优美，符合产品包装的美学追求；另一方面因为传统的云水纹装饰可以为产品增添文化内涵，有利于加深产品的消费者认同感，以此通过溢出效应而抬高产品售价。

图1 广州亚运会颁奖礼服“行云流水”（图片来源于网络）

三、二方连续云水纹参数化数学模型用途

二方连续云水纹参数化数学模型的建立是为了对二方连续云水纹这一传统纹样进行数字化和虚拟化，以供设计师在计算机中生成二方连续云水纹。从实体转向数字虚拟化的二方连续云水纹具有两个主要优势：一方面可以利用参数化技术根据设计要求对二方连续云水纹形态进行调节；另一方面可以利用计算机辅助、3D打印等方式进行结果的快速呈现。它提供给包括平面设计、数字媒体设计、工业设计、手工艺和参数化设计等不同专业一种数字化的二方连续云水纹生成手段，是一种便捷、高效的二方连续云水纹纹样生成系统。并且，此参数化数学模型与当今流行的参数化设计可以紧密结合，运用参数化设计手段结合数学模型设计出具有鲜明参数化设计特征的设计作品。

四、二方连续云水纹参数化数学模型建立

二方连续云水纹参数化数学模型的建立过程，通过系统架构图（图2）进行总体展示。首先，把云水纹拆解成多条独立的曲线，只要建立单根曲线的数学模型，即可通过复制曲线、参数调整和多根曲线拼合的方式来生成参数化云水纹数学模型。而建立单根曲线数学模型的总体思路是把曲线用三角函数进行表达。

图2 （图片来源于作者)

（一）二方连续云水纹数学模型

研究要求把二方连续云水纹拆解成多条形状相似的曲线，并把单个曲线用三角函数表示。作者试图建立一个三角函数模型，涵盖拆解后的所有曲线的表达，即通过改变函数模型的变量来生成不同形状的曲线，再把这些曲线组合成一个竖向的二方连续云水纹。该三角函数在笛卡尔坐标系中的数学表达式为：y=b sin(ax)+cx。其中，a调节曲线图案总体宽度（Width），b调节曲线图案总体长度（Length），c为曲线两个端点的错位程度，在数学模型中表达为曲线的梯度（Gradient）。通过这种方式得到的曲线图像法表达如图3所示（x∈[0,∞)）。[2](P9)得到的函数图像顺时钟旋转90°即是云水纹单线的形态。

图3 （图片来源于作者)

（二）建立双曲线二方连续云水纹数学模型

在a（Width）和c（Gradient）的值固定的情况下，通过对变量b（Length）值进行调整。在同一个笛卡尔坐标系内，在a和c分别为2.5和2.8的固定情形下，b的值输入4.888和9，可以得到两条形状不同的曲线，组合后的图形即为仅有两根曲线的最简单形态的二方连续水云纹（图4）。

（三）多曲线云水纹数学模型

仍然固定a和c的值，当b值分别为4.888、9和13，可以得到三条不同倾角的曲线。组合后的图案相比图4，结构更加复杂，形态也更加优美（图5）。

图4 （图片来源于作者)

在图5三角函数模型的基础上，增大c值来增加函数图像梯度，生成的图像如图6所示。曲线造型与之前相比更加舒展和飘逸，扩展了数字化云水纹的形态范围，给予了设计师更多的选择余地。

图5 （图片来源于作者)

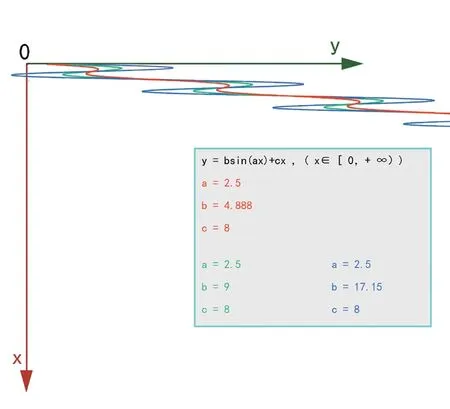
图6 （图片来源于作者)

五、随机形态的二方连续云水纹参数化数学模型建立

至此，研究已经建立了能够模拟多种结构的二方连续云水纹的参数化数学模型，但在实际的设计应用层面，设计师广泛采用的云水纹单体的“长度”（Length，前文有解释）并非固定，而是富有较大变化。为了满足这一要求，研究尝试在上述已有的数学模型中引入数学中的随机变量的概念，以求云水纹单体造型各异，各单体衔接而成的二方连续云水纹形态更具变化。

（一）随机形态的云水纹模型

对比上一节中的数学模型y=b sin(ax)+cx，在此将固定的长度参数b替换为一组独立的随机变量序列{bn:n≥1}。其每一个取值bn代表着对于特定的a和c，在第n个固定的周期范围内的长度参数的取值。随机变量序列{bn}的取值范围可以根据实际需要进行规定。

如此，可以通过一系列数学计算推导，得到如下随机化的二方连续云水纹数学模型：

和前述数学模型相比，a依然调节曲线图案总体宽度（Width），c也依旧表达为曲线的梯度（Gradient）。如果赋予随机变数序列{bn:1≤n≤10}一组值{13，11.4，5.8，5，9.8，9，6.6，12.2，8.2，7.4}，则基于上述模型可以得到如图7云水纹模拟形态。

图7 （图片来源于作者)

可见云水纹的波动长度——即云水纹单体长度表现出了随机性，相比前文单体形态固定的云水纹造型，新的形态整体更富变化，且显得自然灵动。

（二）随机化的复杂结构云水纹模型

类比于文章4.3节，仍然固定a和c的值，取多组不同的随机变量{bn:n≥1}，得到三条不同的随机形态的曲线。组合后的图案即新的二方连续云水纹形态自然（图8），满足了部分设计应用层面对云水纹的造型要求。

图8 （图片来源于作者)

六、总结

二方连续云水纹这一古老装饰纹样，历经千年演变，形态优美，内涵丰富，被广泛运用在包括绘画、器皿装饰、产品设计等不同领域。在当今这个数字化设计大行其道的时代，需要一种方法对二方连续云水纹进行数字化生成，以此来为包括平面设计、服装设计、壁画艺术等在内的各个艺术设计方向提供一种可用计算机进行数字编辑的二方连续云水纹生成方式。

本文首先把二方连续云水纹拆解成为曲线的集合，借助数学手段，通过一个三角函数表达式，采用图像法对单根曲线进行表达。并通过函数表达式中变量的调节，以此来达到改变曲线形态的目的。不同形态的曲线可以组合成为造型各异的云水纹。至此，一种可控形状和大小的数字化二方连续云水纹终于诞生。更进一步，为了模拟单体形态变化的云水纹图案，满足更广泛的社会需求，研究在已有的数学模型基础上，引入随机变量这一数学概念，使得云水纹单体长度各异，因而生成的云水纹造型更富变化，形态也更显自然。由于我国对中国传统文化的不断重视以及对于数字化纹样的强烈需求，在未来的平面设计、壁画设计、服装设计、建筑设计、装置设计等不同领域，数字化的二方连续云水纹定会有一定的需求空间。