平海子水库扩建工程溢洪道优化试验研究
何志亚 汤荣才 冷月华 刘 俊 蒋德才 代 翔
(1.云南省红河州水利水电勘察设计研究院 云南蒙自 661100;2.四川大学水力学与山区河流开发保护国家重点实验室四川成都 610065;3.富顺县古佛镇人民政府 四川自贡 643214)
1 平海子水库概况及试验目的
平海子水库位于云南省泸西县永宁乡境内,现状为一小型水库。为了充分利用永宁乡丰富的水土资源,促进泸西县永宁乡经济可持续发展,拟将原先的小型水库扩建为中型水库,充分发挥农业灌溉、乡镇防洪和水资源调度配置作用[1,2]。扩建后的平海子水库枢纽工程主要由大坝、溢洪道、导流输水放空隧洞组成。拦河坝由1 号、2 号、3 号坝组成;溢洪道布置于1 号坝与2 号坝之间山坡上,为河岸有闸控制溢洪道。
在平海子水库扩建工程的初步设计中,溢洪道由进水渠段、控制段、泄槽Ⅰ段、泄槽Ⅱ段、消力池段和出口明渠段组成,全长468.72 m。控制段采用带胸墙孔口式驼峰堰,堰顶高程与汛期限制水位1 645.84 m齐平,堰宽6 m,堰顶设1 道6 m×4 m 弧形闸门,胸墙高4.8 m。出口采用底流消能,消力池长32.0 m,池宽8.0 m,池深3.2 m。溢洪道1 000年一遇校核洪水下最大下泄流量为98.3 m3/s。溢洪道除泄槽Ⅱ段、出口消力池段采用C35 钢筋混凝土衬砌和出口明渠段采用M7.5 浆砌石衬砌外,其余段均采用C25 钢筋混凝土衬砌。为了验证平海子水库扩建工程溢洪道初步设计的合理性、可靠性和科学性[3],保证溢洪道能够安全稳定的下泄水库流量,并为将来平海子水库的运行管理提供可靠的技术参数,需对原设计方案中的溢洪道开展水工模型试验,复核溢洪道的水力学特性、布置方式和结构尺寸参数的合理性[4],优化溢洪道的设计方案。
基于以上目的,本文开展了平海子水库扩建工程模型溢洪优化试验研究,校核了溢洪道初步设计方案的合理性,针对初设方案存在的问题提出了优化的溢洪道模型,并再次对优化后的溢洪道开展模型试验,测量了不同洪水频率下的泄流量、水流流态、沿程水面线和流速、断面压强和空化数,最后讨论了驼峰堰和宽顶堰的泄流能力。
2 水工模型试验设计
2.1 试验内容
在初步设计报告中,平海子水库扩建工程的设计洪水成果如表1 所示。

表1 平海子水库扩建工程坝址设计洪水成果表
基于以上洪水资料开展此次模型试验,主要是校核原设计报告中溢洪道结构和布置方式的正确性,因此本次水工模型试验主要研究内容为:
1)验证溢流堰(有闸控制驼峰堰)的泄流能力,反演算相对应的流量系数。
2)在最高水位时不同闸门开度下闸后水位爬高,验证闸后边墙高度及长度是否满足要求。
3)验证溢洪道转弯段靠山一侧水面壅高;验证溢洪道在各运行工况下的泄流流速、流态、水面线、泄洪设施压力分布状态及消能防冲建筑物流态及流速分布;验证消力池的体型及布置是否满足各设计工况运行要求,并对其运行工况作出评价;验证下游防冲设计措施是否满足要求;提出消能与防冲的优化措施建议。
4)通过水工模型试验,提出泄槽各段及消力池段在高速水流下流速分布,为相应的混凝土防护提供参考。
5)通过水工模型试验,实测不同洪水频率下泄槽各段、消力池面上的压力分布和水流空化数分布,并提出是否在低压区布设掺气设施,如果须设置掺气设施,提出相应的布置体型。
2.2 模型设计
本模型试验主要涉及溢洪道下泄水流的流态、流速、水深、压强等水力学问题。为了保证水流的运动相似,选择正态模型。水流运行相似按重力相似准则考虑[5-7],根据佛汝德数相似计算,选择1:30 几何比例,在四川大学水力学实验厅建立水工模型并进行模型实验,运动相似和动力相似换算参数如表2 所示。表中:λl和λh为几何比尺下的原型与模型的比例关系;λu速度比例关系;λQ为流量比列关系,λt为时间比例关系;λn为糙率比例关系[8]。制作的模型布置图如图1所示。

表2 模型试验各项相似比尺
试验模型模拟了上游库区、溢洪道、消力池及下游河道等范围,上游和下游河道模型制作采用断面控制,每隔30 m 设一个控制断面,地形变化较复杂情况,每隔15 m 增设控制断面。库区模拟长度为400 m,其中模型进口模拟至0+0,000 桩号上游210 m,模拟高程至1 655 m。模型上游入口流量采用矩形薄壁堰控制。下游模拟了消力池出口下游120 m 长度的河道。溢洪道、消力池均采用有机玻璃制作。根据现场糙率率定,有机玻璃的糙率为0.008 0~0.008 5,根据糙率比尺换算到原型为0.014~0.015,此糙率与原型混凝土糙率基本相同[9],表明模型比尺选为1:30 是合适的。模型的布置如图1 所示。

图1 试验模型场地布置
3 试验结果
3.1 敞泄运行泄流能力
模型试验首先对溢洪道敞泄运行情况下的泄流能力进行了率定。当溢洪道控制段敞泄运行时,综合流量系数按堰流计算,流量系数采用下式(1)计算:

式中:μ——考虑水流行近流速、侧收缩、淹没系数等影响的综合流量系数;
Q——泄流量,m3/s;
B——每个堰孔的净宽度,m;
n——开启孔数,1 孔;
H——堰顶以上的水头,m。这里堰顶高程为1 645.84 m。
敞泄运行时,不同频率洪水情况下的上游库水位与泄流量Q 和流量系数μ 之间的关系如图2 所示,泄流量随着库水位的增加几乎线性的增长,而流量系数在水库水位超过消能防冲洪水频率(P=3.30%)时呈几乎不变趋势,此时μ≈0.366。观测结果表明,不同频率入库洪水流量下,模型实测敞泄情况时,泄流能力皆满足泄洪要求[10],校核和设计工况时水库水位皆低于1 654.14 m。

图2 溢洪道上驼峰堰泄流量和流量系数与水库水位之间的关系
3.2 水流流态
模型试验观测了表1 中不同工况下溢洪道沿程各部位水流流态,如图3 展示了P=3.33%消能防冲工况下溢洪道上下游消力池段水流流态的图片。闸门局开工况条件下,观测成果表明:上游消力池水深较大,并在消力池前端发生水跃,消力池的后半段水体翻出边墙。上游消力池与上半段泄槽I 段水面衔接存在明显跌落,主要是由于上游消力池规模相对较大,在消力池后半段水面较高,而上平段泄槽的底坡较小,从而在消力池中形成堰流(图3a)。
在泄槽I 段中,经上游消力池后的出流水流流速较低,且此段的底坡仅为i=0.01,虽然存在18°的转弯,但由于流速较小且转弯半径较大(转弯半径62.92 m,R/B=10.5),左右两侧水面差较小,水流较为平稳。进入泄槽II 段,此时底坡较大i=0.385,水流速度沿程增加,水面平稳,无其它不良水力现象发生。
桩号(溢)0+249.76~0+281.76 m,即下游消力池段。消能防冲工况时入池流速约24.0 m/s,入池弗劳德数Fr约为9.2,由于原设计消力池水深较浅,出现的问题是:水跃跃首位于消力池中后部,在消力池后部由于受消力坎的阻挡而形成较大的水面翻滚。消力池中、后部水面波动幅度大,表面水体跃出消力池边墙,观测表明整体消力池规模不足(图3b)。

图3 P=3.33%消能防冲工况下溢洪道上下游消力池段水流流态图片
在尾水明渠段,由于下游消力池规模不够,消能不充分,水流在消力池尾坎处上涌,继而以跌流流态与下游退水渠衔接。因退水渠转弯角度大,转弯半径小,消能不充分流速较大,导致在退水渠转弯段,凹岸水位高于凸岸。
综合上述试验成果,分析认为平海子水库扩建工程溢洪道原初步设计方案主要存在的工程问题为:
1)正常水位时,出闸流速约为11.5~12.5 m/s,上游消力池消能作用不明显,由于上游消力池的设置导致在大流量时闸后水流形成淹没水流,反而恶化了闸后水流形态。综合考虑以上因素,建议应取消上游消力池。
2)消能防冲工况Q=81.6 m3/s 时,下游消力池规模不足,消力池边墙高度不够,建议增大消力池规模。
3)闸室上缘进口曲线原为直角,为了改善进流条件,增加闸门局开时的泄流能力,建议闸室上缘进口曲线调整为椭圆或圆形的曲线。
4 溢洪道优化方案
针对上述溢洪道上存在问题和建议,尝试对溢洪道设计进行优化。具体为:1)将闸室上缘进口曲线调整为半径1.0 m 的1/4 圆弧;2)取消上游消力池,闸门出口直接连接上游泄槽I 段;3)增加下游消力池规模,并且使底板降低1.30 m,高程到1 608.87 m,池长增加8.0 m,相应的消力坎桩号为溢0+289.76 m。消力池边墙也由原来的1 617.62 m 增高到1 618.37 m,增加0.75 m。
4.1 敞泄运行泄流能力
当溢洪道控制段敞泄运行时,综合流量系数按堰流计算,采用公式(1)计算得到。与原设计方案相比,取消上游消力池后,驼峰堰敞泄较大流量时,堰后水深减小,水流为自由出流,驼峰堰的泄流能力有所增加,特别是在较大流量时,泄流能力增加明显,在不同频率入库洪水流量下,模型实测敞泄情况时,泄流能力皆满足泄洪要求,校核和设计工况时水库水位皆低于1 654.14 m。如图4 绘制溢洪道优化后泄流量和流量系数与水库水位之间的关系,在取消上游消力池后,泄流量和流量系数明显增加。以设计下泄流量为例,Q=88.0 m3/s 时,原设计方案敞泄1 650.19 m,推荐方案上游库水位下降到1 649.76 m(降低了0.43 m);相对应的流量系数由原来的0.366 增加到0.427,泄流能力增加17%。

图4 溢洪道优化后泄流量和流量系数与水库水位之间的关系
4.2 控制运行泄流能力
当溢洪道驼峰堰闸门局部开度运行时,闸孔呈有压流流态,综合流量系数按闸孔出流计算,流量系数采用如下公式(2)计算:

式中,A 为每个闸孔的过水面积,m2。需特别说明的是,简化过流面积A=eB,B 为闸门宽度,B=6.0 m;e 为闸门开度,e=Hi-H0,Hi为闸门底高程,H0为堰顶高程,H0=1 645.84 m;其余符号意义同上。
图5 描述了上游不同水库水位、三种闸门开度下的泄流量和流量系数与水库水位间的关系。结果表明,在同一开度e 下,随着库水位的增加,流量逐渐地增加;随着开度的变大,对应的流量系数减小。同时可以发现,在水位1 654.14 m 下,开度为0.9 m、1.2 m 和1.5 m 时对应的泄流量分别为64.24 m3/s、82.35 m3/s和98.30 m3/s,对应的流量系数分别为0.932、0.896、0.856,比通常的闸孔出流的流量系数大。主要原因如下:常见的闸孔出流的垂直收缩系数一般在0.63~0.79 之间,而本工程中驼峰堰闸孔出流的垂直收缩系数表寻常的大的多;此外,公式(2)中过流面积采用A=eB,而实际过流面积为A=e1B,e1为进水口底板高程到闸门底高程的距离。

图5 不同闸门开度下的泄流量和流量系数与库水位间的关系
在初步设计时,因水力学公式适用条件限制,部分水位—开度下,控制段泄流量难以计算,本次模型试验可对控制段全工况下泄流能力进行测算,根据实测敞泄和控泄时的流量系数,反演推算出不同开度,不同水位时的流量关系,图6 绘制了全开度的水位—开度—流量关系曲线,用于指导水库泄洪时溢洪道的准确调度。

图6 驼峰堰水位—开度—流量关系曲线
由于平海子水库扩建后是一项农业灌溉和乡镇防洪的综合利用性水利工程。水库调度的基本原则是:20年一遇及以下洪水主要保护下游的同时确保水库自身安全,20年一遇以上洪水不造成人为加大出库洪水带来灾害的前提下对超出下游防洪标准洪水调节,保证大坝安全。水库溢洪道闸门控制段需频繁、快速、准确地控制闸门开度以满足水库在不同时段的泄洪要求,由于操作过程闸门开度较小,建议加强闸门对于水位和流量的控制,其本质是避免闸门误操作而造成的人为洪水。
4.3 沿程水面线
对不同工况下的溢洪道上的沿程水面线进行了观测。图7 展示了设计工况(P=2.00%)和校核工况(P=0.10%)下的溢洪道右岸水面线均值和最大值分布情况。可以看出,在进口段和闸室段,由于在试验中库水位始终保持在1 654.14 m,进水渠段水流流速较小,水面平稳。闸室段由于驼峰堰体型较小,水流受驼峰堰堰顶和闸底影响,在堰顶处存在局部隆高(如图中所示),但最大深度小于闸门支铰高程。闸门支铰处最高水深出现在校核工况时,水深约为1.56 m,对应的水面高程为1 646.60 m。
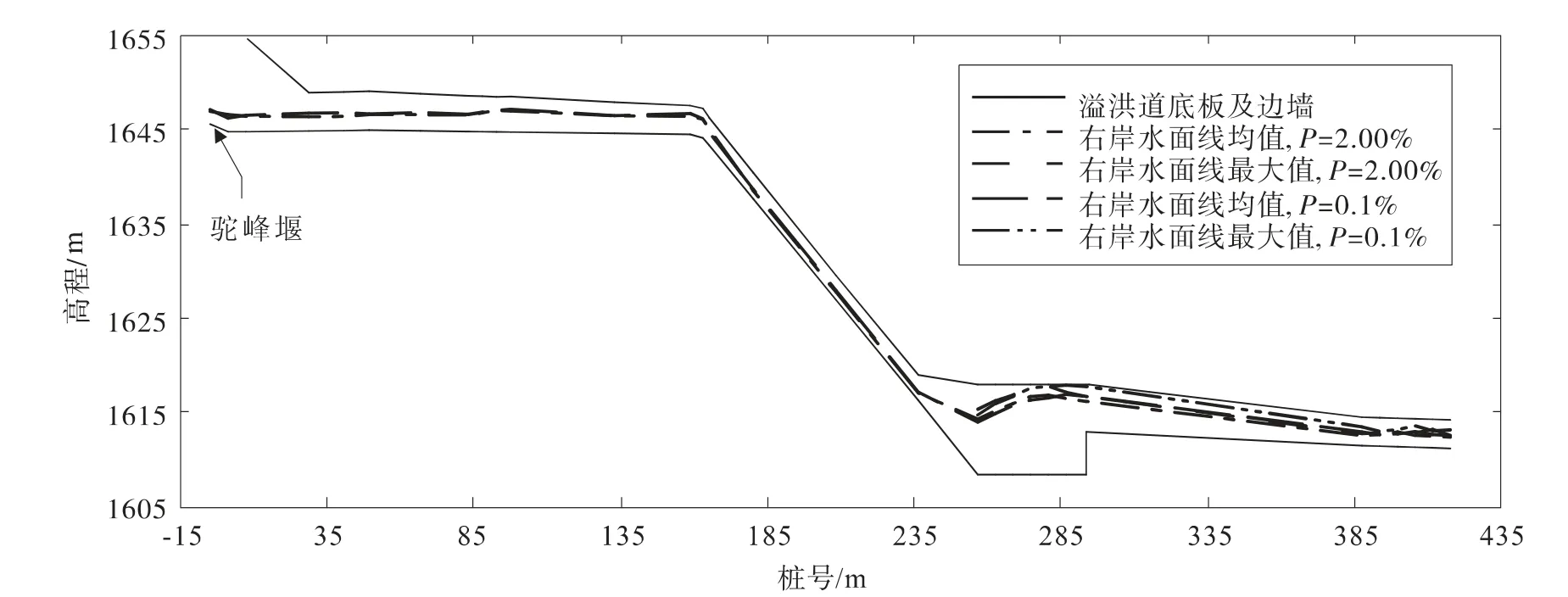
图7 工况P=2.00%和P=0.10%下溢洪道上的水面线均值和最大值
对于消力池入池段和消力池段,即桩号(溢)0+237.37~0+293.27 m。不同下泄流量时,入池流速约22.0~25.0 m/s,入池Fr 数约9.0,消力池中前端水体紊动剧烈,中后部处于跃后调整段,相对平稳。不同流量时,随着流量增大,消力池内水流紊动强度增加,水面波动幅度相应增加。在校核工况下(Q=98.3 m3/s,P=0.1%),消力池内平均水深范围为6.45~8.47 m,最高水位范围为7.50~9.42 m。设计消力池边墙高度为9.5 m,可以满足相应的挡水要求。
水流流出消力池后以跌流流态与下游尾水明渠衔接。因退水渠转弯角度大,转弯半径小,左右岸有一定的水面差。校核工况(Q=98.3 m3/s,P=0.10%),尾水渠内左岸平均水深范围为2.34~2.73 m,最高水位范围为2.80~3.45 m,右岸平均水深范围为1.20~1.65 m,最高水位范围为1.56~2.25 m,最大横向水面差为1.50 m,出现在桩号溢0+393.30 m 处。
4.4 沿程流速
为了获得溢洪道上不同位置处的流速情况,分别沿着溢洪道的中轴线、左岸和右岸三个纵向方向,进行了从底板到水流自由表面的三个垂直高程位置(即底板、中间和表面)的流速测量。图8 绘制了不同工况下水流沿溢洪道的断面最大流速。测量结果表明,在溢洪道泄槽I 段,由于上平段坡度较缓(底坡i=0.01),出闸水流流速沿程减小,流速大约从闸孔出流时12 m/s降低到7 m/s。进入泄槽II 段,由于此段坡度较陡(底坡i=0.38),流速沿程快速增加,在进入消力池时流速甚至增加到22~24 m/s。

图8 不同工况下溢洪道沿程最大流速分布
在进入消力池段后,消力池前20.0 m 的临底流速较大,校核工况下的最大临底达15.0 m/s,此后由于消力池的消能作用,临底流速快速减小。因消力池消能充分,在流出消力池时的流速小于4 m/s。在消力池出口以跌流流态与下游尾水渠衔接。因尾水渠转弯角度大,转弯半径小,左右岸有一定的速度差。在设计工况(P=2.0%)下,尾水渠内左岸速度范围为5.20~6.76 m/s,右岸平均速度范围为6.01~7.00 m/s,左右侧最大流速差为1.33 m/s。
4.5 压强与空化数
模型试验分别观测了不同工况下溢流段、泄槽段以及消力池段的压强,并计算了相应的水流空化数,公式如下:

式中,σ 为水流空化数;h0为参考断面时均压力水头,m;ha为溢洪道所在地区大气压;hv为水的气化压力水柱,m,与水温有关[10],本工程取hv=0.238×9.8 kPa;v0为参考断面平均流速,m/s;▽为当地海拔高度,取1 832 m。
图9 绘制了不同工况下的断面时均压强和空化数随溢洪道纵向变化的曲线分布。结果表明,在上平段除了在驼峰堰后出现局部负压外,上平段的压强范围变化不大,为0.9~1.62×9.8 kPa。进入消力池后,数据压强皆为正压,各工况下的压强分布约为5.85~8.10×9.8 kPa。表明消力池的设计是合适的。

图9 不同工况下断面时均压强和空化数分布
空化数计算结果表明,各种工况下溢洪道沿程空化数皆大于0.3,随着泄流量的增加,断面空化数减小,表明较高的流速对应更高的空化数。在设计工况(Q=88.0 m3/s,P=2.0%)时,最小空化数为0.34,出现在桩号(溢)0+208.32 m 处,此处流速为23.48 m/s,根据文献[11]“防空蚀设计”中的相关条文,本工程可以不设掺气设施,但建议严格陡槽段过流面的平整度。
5 讨论宽顶堰方案
为了保护永宁乡沿岸666.6 hm2耕地、1.09 万人口和下游名胜古迹、国家地质公园,平海子水库需要控制下泄流量。在溢洪道敞泄时的泄流能力完全足够满足水库自身安全泄洪要求,但提高下游河岸两侧的防洪标准,下泄流量受闸门控制。校核工况时,溢洪道闸门为局部开启,孔口为有压出流,此种工况时,驼峰堰较宽顶堰泄流能力强的优势不显著,最终的下泄流量都由闸门开度大小决定[12]。在初步设计时提供了驼峰堰和宽顶堰两种调洪演算结果,上文研究了采用驼峰堰时的泄流量、溢洪道流速和压强等,因此有必要讨论溢洪道采用宽顶堰时的泄流量参数。宽顶堰方案主要布置在(溢)0-010.00~0+008.00 范围内,堰顶为1 645.84m,在0+008.00~0+160.57.00 范围内坡度为0.01,其后体型与驼峰堰相同。
运用公式(1)对使用宽顶堰溢流时溢洪道敞泄和控泄运行情况下的泄流能力进行了率定。图10 展示了宽顶堰和驼峰堰泄流能力的比较。可以看出,宽顶堰在不同的洪水频率下的泄流能力同样都满足泄洪要求。宽顶堰方案与驼峰堰方案相比较,驼峰堰的泄流能力略大于宽顶堰。例如在设计流量Q=87.6 m3/s,驼峰堰敞泄时库水位为1 649.73 m,宽顶堰敞泄时库水位为1 650.23 m,水位相差0.50 m;驼峰堰敞泄时流量系数为0.427,宽顶堰敞泄时库水位为0.358,两者相差0.069,同等条件下驼峰堰的泄流能力约大19%。对于闸门同一开度条件下,与驼峰堰方案相比,宽顶堰的泄流能力减小明显,这主要是受闸门出闸后流态和实际过流断面影响有关。并且,宽顶堰结构简单,施工方便,因此在其他经济条件相差不大的情况下,建议选择驼峰堰增大溢流量。

图10 宽顶堰较驼峰堰溢洪道敞泄和控泄泄流能力比较
6 结论
本文针对平海子扩建工程溢洪道初步设计方案,采用正态模型和重力相似准则,建立水工模型,对原设计方案不同洪水频率开展了试验观测,可得出以下结论:
1)原设计方案水流流态表明上游消力池水深较大,在消力池中形成堰流;下游消力池规模不足,水跃发生于消力池中后部并跃出边墙,建议取消原设计方案中的上游消力池,并增加下游消力池规模。
2)溢洪道优化后,敞泄和控泄运行皆能满足设计要求,在同一开度下,随着库水位的增加,流量逐渐地增加,但随着开度的变大,对应的流量系数减小;推算了设置驼峰堰时闸门全开度下的流量—开度—水位关系曲线,用于指导工程调度。
3)最大洪水频率下溢洪道沿程的水面线不超过9.42 m,小于边墙高9.5 m;消力池前段最大临底流速约为15.0 m/s,并随消能作用而快速减小;各工况下沿程皆为正压,且最小空化数大于0.3,可不设掺气设施,但建议严格陡槽段过流面的平整度。
4)讨论了溢洪道泄流采用驼峰堰和宽顶堰的泄流能力,驼峰堰的泄流量明显大于宽顶堰。

